Przeczytaj
Liczby naturalne
Liczby naturalne to liczby całkowite nieujemne: , , , , , , , Zbiór liczb naturalnych oznaczamy wielką literą .
Możemy zatem zapisać, że: .
Liczby wielokątne
Liczby wielokątne –kątne to kolejne liczby otrzymane poprzez dodawanie początkowych liczb zaczynających się od i różniących się od siebie o .
Początkowe liczby z lewej strony kolumny to liczby różniące się o , natomiast te z prawej to liczby wielokątne:
, , , , liczby naturalne , , , ,
, , , , liczby trójkątne , , , ,
, , , , liczby kwadratowe , , , ,
, , , , liczby pięciokątne , , , ,
, , , , liczby sześciokątne , , , ,
, , , , liczby siedmiokątne , , , ,
, , , , liczby ośmiokątne , , , ,
Zapoznaj się z graficznym sposobem budowania liczb wielokątnych.



Liczbom wielokątnym odpowiadają w trójwymiarze liczby piramidalne.

Suma trzech liczb czworościennych daje liczbę trójkątną.

Jedno z odkrytych przez Diofantosa twierdzeń brzmi:
Ośmiokrotnie wzięta liczba trójkątna powiększona o jedność jest zawsze kwadratem.
To znaczy, że ośmiokrotność dowolnej liczby trójkątnej powiększona o jeden jest zawsze liczbą kwadratową.
Liczby palindromiczne
Liczba palindromiczna to liczba, która przy czytaniu jej cyfr od lewej strony do prawej jest jednakowa, jak czytana od prawej do lewej. Liczby takie nazywane są także liczbami symetrycznymi. Przykłady takich liczb to: , , , ,
Każda liczba palindromiczna w systemie dziesiętnym, złożona z parzystej liczby cyfr, jest podzielna przez .
PalindromyPalindromy mogą być kwadratami liczb naturalnych
i ich sześcianami
.
Liczby Lychrel
W roku amerykański matematyk Derrick Lehmer opisał pewną własność liczb: jeśli do wybranej liczby dodamy ją samą, ale zapisaną w odwrotnej kolejności i z otrzymaną sumą oraz z każdą następną postąpimy tak samo, to w którymś cyklu, jako kolejna suma pojawi się palindrompalindrom, np.
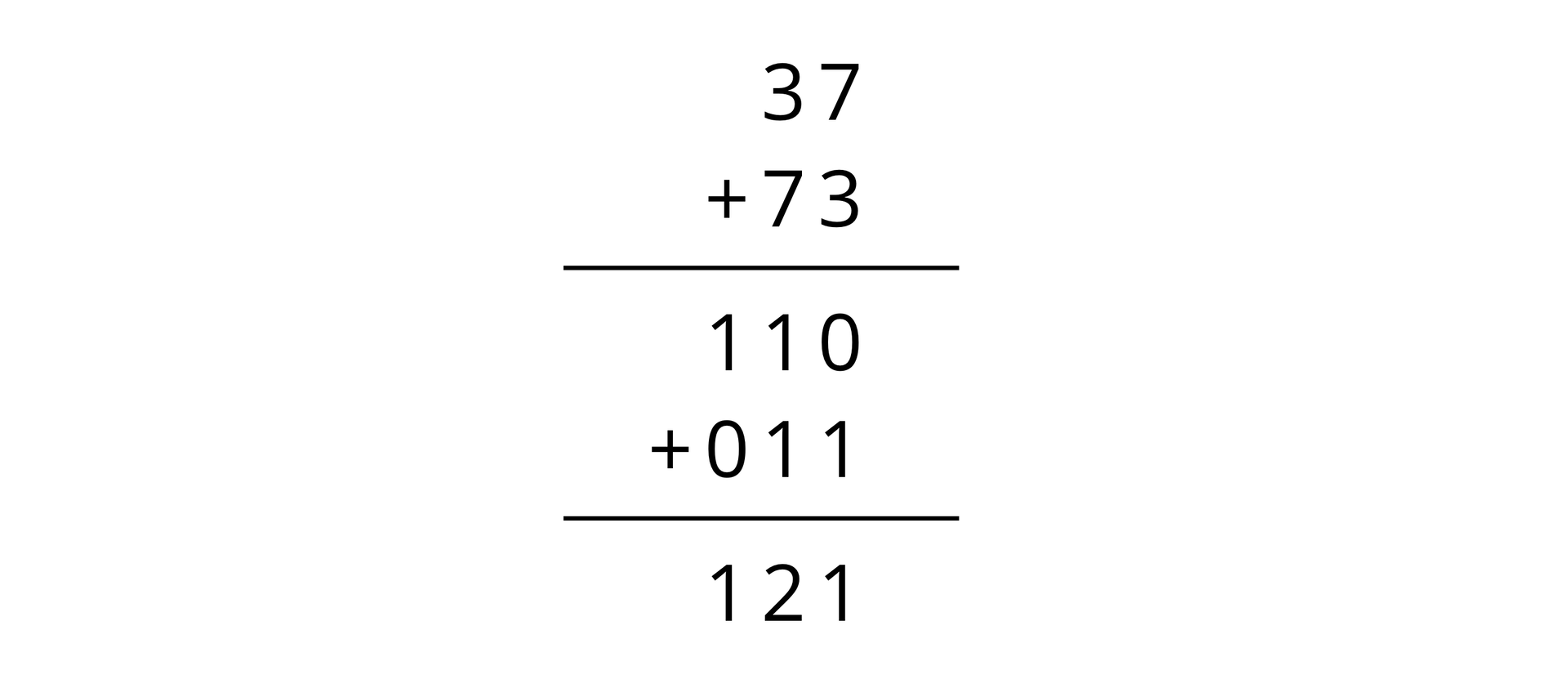
Większość małych liczb większych od dociera do palindromu w jednym kroku.
jest pierwszą liczbą wymagającą dwóch kroków .
– wymaga trzech kroków ,
– wymaga aż czterech
(same sumy: ).
Liczbą, przy której trzeba się solidnie napracować, jest – palindrom pojawia się dopiero jako –ta liczba w ciągu sum: .
To jednak nic w porównaniu z „gehenną”, którą oferuje liczba . Lehmer wykonał przed laty blisko sto dodawań – bezskutecznie. Nie omieszkał jednak zauważyć, że –ta suma jest bardzo bliska docelowej, wygląda bowiem tak: . Zapewne ta obiecująca bliskość skłoniła go do postawienia hipotezy, że każda liczba poddana opisanemu procesowi zmieni się w palindrompalindrom – wszystko jest tylko kwestią etapu, w którym to nastąpi. to nie jedyna „krnąbrna” liczba, ale stosunkowo mała, więc nią przede wszystkim zajęli się programiści, gdy do akcji wkroczyły komputery.
Jako pierwszy wyzwanie podjął John Walker – założyciel znanej firmy Autodesk, zajmującej się oprogramowaniem komputerowym. W roku Walker uruchomił program na stacji roboczej Sun 3/260. Po blisko trzech latach nieprzerwanej pracy i wykonaniu operacji „odwróć i dodaj” komputer dotarł do liczby złożonej z miliona cyfr i się zatrzymał. PalindromuPalindromu nie było. Następcy Walkera posuwali się coraz dalej, korzystając z coraz lepszych komputerów. Jeden z nich nadał i pozostałym równie opornym liczbom nazwę, która się przyjęła – liczby Lychrel – prawdopodobnie jest ona anagramem imienia Cheryl.
Aktualny rekord w wędrówce od do palindromu należy do francuskiego programisty Romaina Dolbeau. Pod koniec roku dotarł on po bilionie kroków do liczby złożonej z cyfr, jednak nie osiągnął celu. Wydaje się, że dalszej eksploracji nie będzie. Szansa na dotarcie do gigantycznego palindromu maleje wraz z wydłużaniem się sumy – praktycznie jest już równa zeru. Wiele wskazuje na to, że hipotezę podaną przez Lehmera należy uznać za błędną. Tym bardziej, że dla systemów liczbowych o mniejszych podstawach niż dziesiętny udowodniono, że niektóre liczby poddawane operacji „odwróć i dodaj” nigdy nie zmienią się w palindrom.
W systemie dwójkowym najmniejszą taką liczbą jest , odpowiadająca liczbie w systemie dziesiętnym. Niemiecki matematyk Roland Sprague jeszcze w latach –tych udowodnił, że przekształcenie jej w palindrompalindrom jest niemożliwe. Zauważył, że w ciągu sum, poczynając od czwartej, cyklicznie powtarzają się cztery schematy liczb. Na przykład, dla czwartej sumy równej schematem jest . Dla tej sumy , dla ósmej to , dla dwunastej itd. – schemat pozostaje taki sam. Zarówno ten schemat, jak i każdy z trzech pozostałych wyklucza pojawienie się palindromu. Znalezienie dowodu dla układu dziesiętnego ostatecznie rozwiązałoby problem i odesłało liczby Lychrel do lamusa. Niestety, dotąd nikomu się to nie udało.
Działania arytmetyczne na liczbach naturalnych w systemie dziesiątkowym
Dodawanie: .
Obiekty dodawane to składniki, wynik dodawania nazywa się sumą, a znak działania to „”.
Odejmowanie: .
Obiekty odejmowane to odjemna i odjemnik, wynik odejmowania nazywa się różnicą, a znak działania to „”.
Mnożenie: .
Obiekty mnożone to czynniki, wynik mnożenia nazywa się iloczynem, a znak działania to „”.
Dzielenie: .
Obiekty dzielone to dzielna i dzielnik, wynik dzielenia nazywa się ilorazem, a znak działania to „”.
Słownik
liczba (lub wyraz), która czytana z prawej do lewej, brzmi tak samo jak czytana z lewej do prawej