Obliczymy pole i objętość ośmiościanu foremnego o krawędzi długości $6$ $\mathrm{cm}$ oraz pole kuli opisanej na tym ośmiościanie.

Rozwiązanie

$P_c=2a^2\sqrt{3}=2·6^2·\sqrt{3}=72\sqrt{3} {\mathrm{cm}}^2$

$V=\frac{a^3\sqrt{2}}{3}=\frac{6^3\sqrt{2}}{3}=72\sqrt{2} {\mathrm{cm}}^3$

Obliczymy długość promienia kuli opisanego na wielościanie:

$R=\frac{a\sqrt{2}}{2}=3\sqrt{2} \mathrm{cm}$

Zatem pole kuli wynosi:

$P=4\pi R^2=4\pi ·\left(3\sqrt{2}\right){}^2=72\pi {\mathrm{cm}}^2$

Środki ścian sześcianu są wierzchołkami ośmiościanu. Obliczymy objętość tego ośmiościanu, jeśli objętość sześcianu wynosi $512$.

Rozwiązanie

Wykonajmy rysunek pomocniczy:

RPpZRjJgcsvoA

Ilustracja przedstawia ośmiościan znajdujący się wewnątrz sześcianu. Krawędzie dolnej podstawy sześcianu to A  B D C, krawędzie górnej podstawy sześcianu to $A\text{'}$ $B\text{'}$ $D\text{'}$ $C\text{'}$. Na środku ściany ABDC znajduje się się punkt L. Na środku ściany $A\text{'}$$B\text{'}$$C\text{'}$$D\text{'}$ znajduje się się punkt K. Na środku ściany A$A\text{'}$C $C\text{'}$ znajduje się punkt G. Na środku ściany A $A\text{'}$B $B\text{'}$ znajduje się punkt H. Na środku ściany B $B\text{'}$D $D\text{'}$ znajduje się punkt I. Na środku ściany D $D\text{'}$C $C\text{'}$ znajduje się punkt J. Punkty L, K, G, H, I, J są wierzchołkami ośmiościanu. Literą M oznaczono środek ośmiościanu znajdujący się w punkcie przecięcia wysokości opuszczonej z wierzchołka K na płaszczyznę GHIJ oraz przekątnych GI oraz HJ.

Niech $a$ - długość krawędzi sześcianu. Wówczas $a^3=512$, zatem $a=8$.

Zauważmy też, że $\left|HJ\right|=8$. Odcinek ten jest przekątną kwadratu $GHIJ$. Możemy więc obliczyć długość krawędzi ośmiościanu foremnego. Oznaczmy ją jako $x$.

$x\sqrt{2}=8$

$x=\frac{8}{\sqrt{2}}=4\sqrt{2}$

Możemy więc policzyć objętość ośmiościanu:

$V=\frac{{\left(4\sqrt{2}\right)}^3\sqrt{2}}{3}=\frac{128\sqrt{2}·\sqrt{2}}{3}=\frac{256}{3}$

Przekątna ośmiościanu ma długość $s$. Obliczymy jego pole i objętość.

Rozwiązanie

Wykorzystamy wzór na przekątną ośmiościanu o krawędzi długości $a$:  $d=a\sqrt{2}$.

Zatem powstaje równanie:

$s=a\sqrt{2}$

$a=\frac{s\sqrt{2}}{2}$

Możemy więc policzyć pole i objętość ośmiościanu:

$P_C=2a^2\sqrt{3}=2·{\left(\frac{s\sqrt{2}}{2}\right)}^2\sqrt{3}=2·\frac{2s^2}{4}\sqrt{3}=s^2\sqrt{3}$

$V=\frac{{\left(\frac{s\sqrt{2}}{2}\right)}^3\sqrt{2}}{3}=\frac{\frac{2\sqrt{2}{s}^3}{8}·\sqrt{2}}{3}=\frac{s^3}{6}$

Promień kuli wpisanej w ośmiościan foremny jest o $\sqrt{6}$ krótszy od promienia kuli opisanej na ośmiościanie foremnym. Obliczymy pole powierzchni całkowitej i objętość bryły.

Rozwiązanie

Oznaczmy jako $a$ długość krawędzi ośmiościanu. Możemy więc ułożyć równanie:

$\frac{a\sqrt{6}}{6}+\sqrt{6}=\frac{a\sqrt{2}}{2}$

$a\sqrt{6}+6\sqrt{6}=3a\sqrt{2}$

$6\sqrt{6}=a\left(3\sqrt{2}-\sqrt{6}\right)$

$a=\frac{6\sqrt{6}}{3\sqrt{2}-\sqrt{6}}$

Usuńmy niewymierność z mianownika:

$a=\frac{6\sqrt{6}}{3\sqrt{2}-\sqrt{6}}·\frac{3\sqrt{2}+\sqrt{6}}{3\sqrt{2}+\sqrt{6}}=\frac{6\sqrt{6}\left(3\sqrt{2}+\sqrt{6}\right)}{18-6}=\frac{18\sqrt{12}+36}{12}=\frac{36\sqrt{3}+36}{12}=3\sqrt{3}+3$

Obliczmy więc pole i objętość ośmiościanu:

$P_c=2a^2\sqrt{3}=2·{\left(3\sqrt{3}+3\right)}^2\sqrt{3}=72\sqrt{3}+108$

$V=\frac{{(3\sqrt{3}+3)}^3\sqrt{2}}{3}=54\sqrt{6}+90\sqrt{2}$

Ośmiościan $ABCDEF$ o krawędzi $a$ przecięto płaszczyzną równoległą do płaszczyzn trójkątów $BCE$ i $AFD$ oraz przechodzącą przez środki pozostałych krawędzi (zobacz rysunek). Obliczymy pole otrzymanego przekroju.

R6ZWFOS2HzXYg

Ilustracja przedstawia ośmiościan foremny jego górny wierzchołek oznaczono literą E, dolny wierzchołek oznaczono literą F, pozostałe wierzchołki podpisano A B C D. Wierzchołki płaszczyzny leżą na następujących krawędziach ośmiościanu: AE, ED, CD, CF, BF, AB.

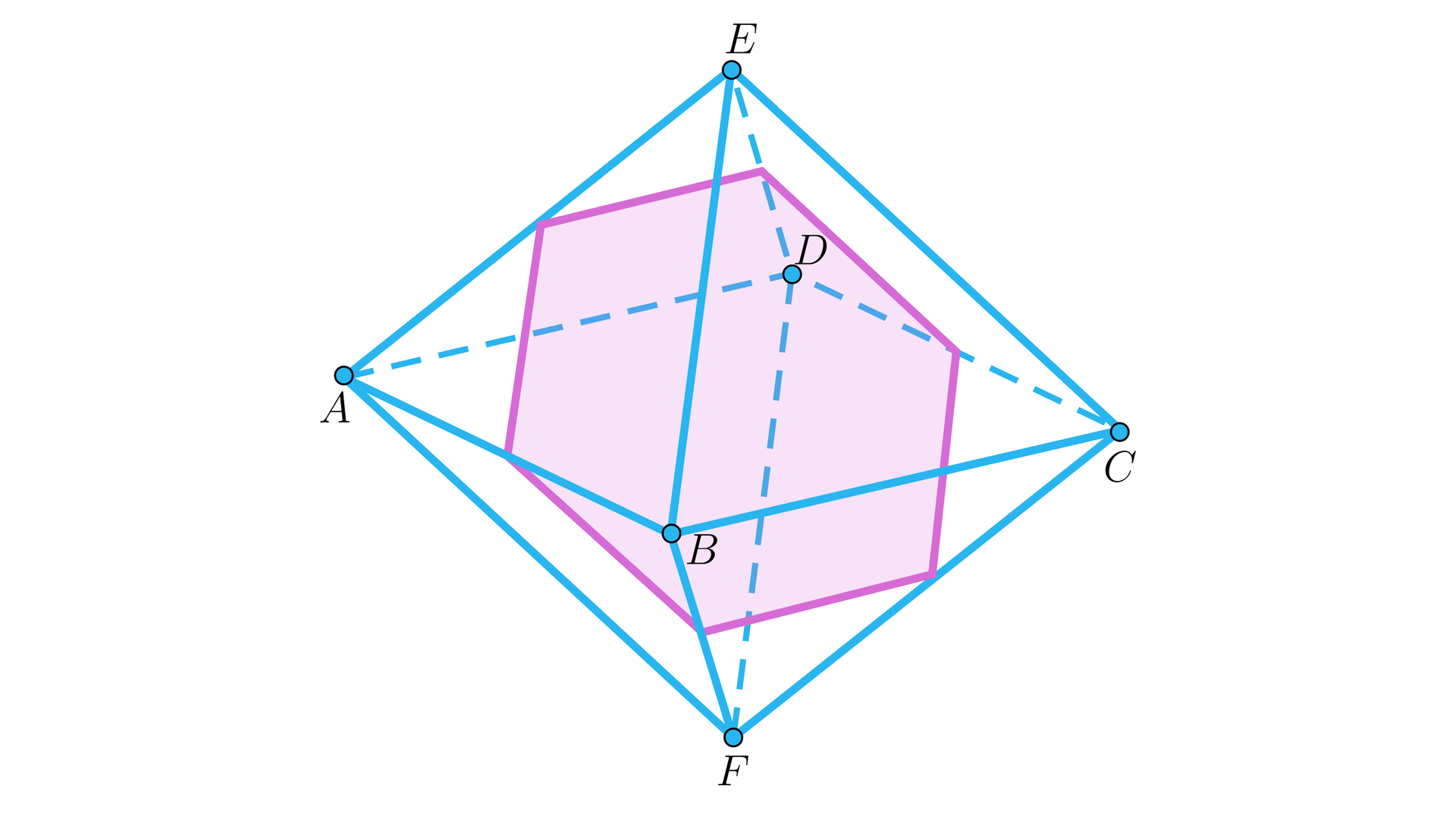
Rozwiązanie

Przekrojem jest sześciokąt foremny o krawędzi dwa razy krótszej od krawędzi ośmiościanu. Pole przekroju jest zatem równe:

$P=\frac{6·{\left(\frac{1}{2}a\right)}^2\sqrt{3}}{4}=\frac{6a^2\sqrt{3}}{16}=\frac{3a^2\sqrt{3}}{8}$

bryła geometryczna, ograniczona przez tak zwaną powierzchnię wielościenną, czyli powierzchnię utworzoną z wielokątów o rozłącznych wnętrzach i każdym boku wspólnym dla dwóch wielokątów; każdy wielościan utworzony jest ze ścian – wielokątów, które razem tworzą powierzchnię wielościanu

wszystkie figury, które mają taką samą liczbą boków, o takiej samej długości oraz kąty między tymi bokami mają takie same wartości; figury przystające mają więc takie samo pole powierzchni i idealnie się na siebie nakładają