Przeczytaj
Liczby pierwsze i bliźniacze
Liczby pierwsze bliźniacze to kolejne liczby pierwsze, których różnica wynosi 2.
Przykładem takich liczb są pary: i lub i .
Przygotujmy kod, który – wśród liczb pierwszych – pozwoli odnaleźć liczby bliźniacze. W tym przypadku przygotujemy funkcję obliczającą liczby pierwsze w przedziale metodą Eratostenesa (więcej na jej temat znajdziesz w e‑materiale Sito EratostenesaSito Eratostenesa). Następnie zbadamy, które spośród znalezionych liczb pierwszych spełniają warunki liczb bliźniaczych. Działanie naszego programu sprawdzimy, szukając liczb bliźniaczych do liczby 80.
Specyfikacja:
Dane:
n– górna granica przedziału; liczba naturalna, większa od 2
Wynik:
Program ma znaleźć i wypisać pary liczb bliźniaczych w zadanym przedziale.
Zaczynamy od zaimplementowania funkcji wyszukującej wszystkie liczby pierwsze w przedziale . Tworzymy definicję naszej funkcji. Następnie przygotowujemy dwie listy: lista_liczb, która będzie przechowywała znalezione liczby pierwsze, oraz lista, która będzie służyła do przechowywania wykreślonych liczb (wartość True oznacza, że liczba nie została jeszcze wykreślona).
Następnie tworzymy pętlę, której zadaniem będzie znajdowanie najmniejszej niewykreślonej liczby w danym momencie. Będzie ona działała w przedziale . W celu obliczenia pierwiastka, importujemy z biblioteki math funkcję sqrt. Jeżeli obecnie sprawdzana liczba nie była jeszcze wykreślona, to zaczynamy wykreślanie wszystkich jej wielokrotności z tablicy lista. W tym celu tworzymy pętlę odpowiadającą za wyznaczanie kolejnych wielokrotności liczby indeks. Swoje działanie będzie zaczynała od jej dwukrotności i zwiększała wartość o wartość sprawdzanej liczby.
Kolejnym krokiem będzie odszukanie liczb pierwszych, czyli tych, które nie zostały wykreślone z listy lista. W tym celu tworzymy pętlę, która zapisuje te liczby do listy lista_liczb. Na końcu zwracamy nasz wynik, czyli listę liczb pierwszych znalezionych w podanym przedziale.
Przejdźmy teraz do wyszukiwania liczb bliźniaczych. W tym celu, za pomocą zaimplementowanej funkcji, wyszukamy najpierw wszystkie liczby pierwsze z przedziału
Tworzymy listę liczby_blizniacze, która będzie przechowywała znalezione pary liczb bliźniaczych. Następnie, za pomocą pętli, sprawdzamy każde dwie kolejne znalezione liczby pierwsze z tablicy liczby_pierwsze.
Oto kod całego programu:
Wynik wywołania kodu będzie następujący:
Liczby doskonałe
Liczby doskonałe to liczby naturalne, które są jednocześnie sumą wszystkich swoich dzielników właściwychdzielników właściwych.
Przykładem takiej liczby jest , ponieważ spełnia ona przedstawiony warunek: .
Jedną z możliwości odnajdywania liczb doskonałych jest sposób opisany przez Euklidesa w IX księdze Elementów.
W celu znalezienia liczby doskonałej należy obliczyć sumy kolejnych potęg liczby 2, a jeśli taka liczba okaże się liczbą pierwszą, wówczas trzeba pomnożyć ją przez ostatni składnik dodawania – w ten sposób otrzymamy liczbę doskonałą.
Przykład:
Badamy kolejno wyrazy:
- jest liczbą pierwszą, czyli jest liczbą doskonałą;
- jest liczbą pierwszą, czyli jest liczbą doskonałą;
- nie jest liczbą pierwszą;
- jest liczbą pierwszą, czyli jest liczbą doskonałą;
itd.
Napiszmy program, który wypisze listę liczb doskonałych w przedziale . Działanie naszego programu przetestujemy dla n = 10000.
Specyfikacja:
Dane:
n- górna granica zakresu; liczba naturalna
Wyniki:
Program ma znaleźć i wypisać liczby doskonałe z podanego przedziału.
Zacznijmy od zdefiniowania funkcji pomocniczej suma_dzielnikow(liczba), która będzie zwracała sumę dzielników właściwych danej liczby. W tym celu, zaczynając od 1, sprawdzamy, czy kolejne liczby są dzielnikami liczby liczba (wynik operacji modulo, operator %, będzie równy 0). Jeżeli tak, to dodajemy do sumy wartość tego dzielnika.
Następnie stworzymy funkcję czy_doskonala(liczba), która będzie odpowiadała na pytanie, czy dana liczba jest liczbą doskonałą. W tym celu sprawdzamy, czy liczba jest równa sumie dzielników tej liczby.
Na samym końcu tworzymy pętlę, która będzie szukała liczb doskonałych w zadanym przedziale. Sprawdzamy kolejne liczby - jeżeli spełniają warunki, zapisujemy je w liście wynikowej i wyświetlamy nasze rozwiązanie.
Oto kod całego programu:
Wynik wywołania kodu będzie następujący:
Oprócz liczb, które znaleźliśmy, kolejnymi liczbami doskonałymi są liczby: , , .
Wszystkie znane dotychczas liczby doskonałe są parzyste. Nie udało się jednak do tej pory udowodnić, że liczby doskonałe nieparzyste nie istnieją.
Zaczynamy od kodu z Przykładu 2.
Możemy sprawdzić, ile czasu zabiera naszemu komputerowi policzenie kolejnych liczb i zwizualizować te czasy za pomocą modułu matplotlibmatplotlib.
W tym celu, na samej górze pliku, importujemy odpowiednią bibliotekę do tworzenia wykresów (matplotlib.pyplot) i ustawiamy jej alias plt. Potrzebna nam będzie również funkcja perf_counter() z biblioteki time, która umożliwi dokładny pomiar czasu.
Na początku przygotowujemy dwie tablice: X, która będzie przechowywała wartości na osi OX oraz czasy, która będzie przechowywała czas, jaki upłynął od rozpoczęcia wykonywania obliczeń, do ukończenia sprawdzania każdej liczby, czy jest ona liczbą doskonałą.
Rozpoczynamy pomiar, zapisując w zmiennej czas_startu czas rozpoczęcia wykonywania obliczeń. Ponieważ zależy nam na dokładności obliczeń, używamy do tego funkcji perf_counter() z biblioteki time.
Następnie modyfikujemy pętlę, która odpowiadała za sprawdzanie kolejnych liczb, czy są liczbami doskonałym. Po sprawdzeniu każdej liczby dodajemy do utworzonych tablic wartości: do tablicy X dodajemy liczbę, którą sprawdziliśmy, a do tablicy czasy - czas, jaki upłynął od rozpoczęcia obliczeń.
Ostatnim krokiem będzie wyświetlenie wykresu. W kolejnych krokach używamy funkcji:
plt.plot()- rzutujemy na wykres kolejne punkty o współrzędnych z tablicXorazczasy,plt.xlabel()- ustawiamy opis osi X,plt.ylabel()- ustawiamy opis osi Y,plt.grid()- włączamy wyświetlanie siatki na wykresie,plt.show()- wyświetlamy wykres.
Oto kod całego programu:
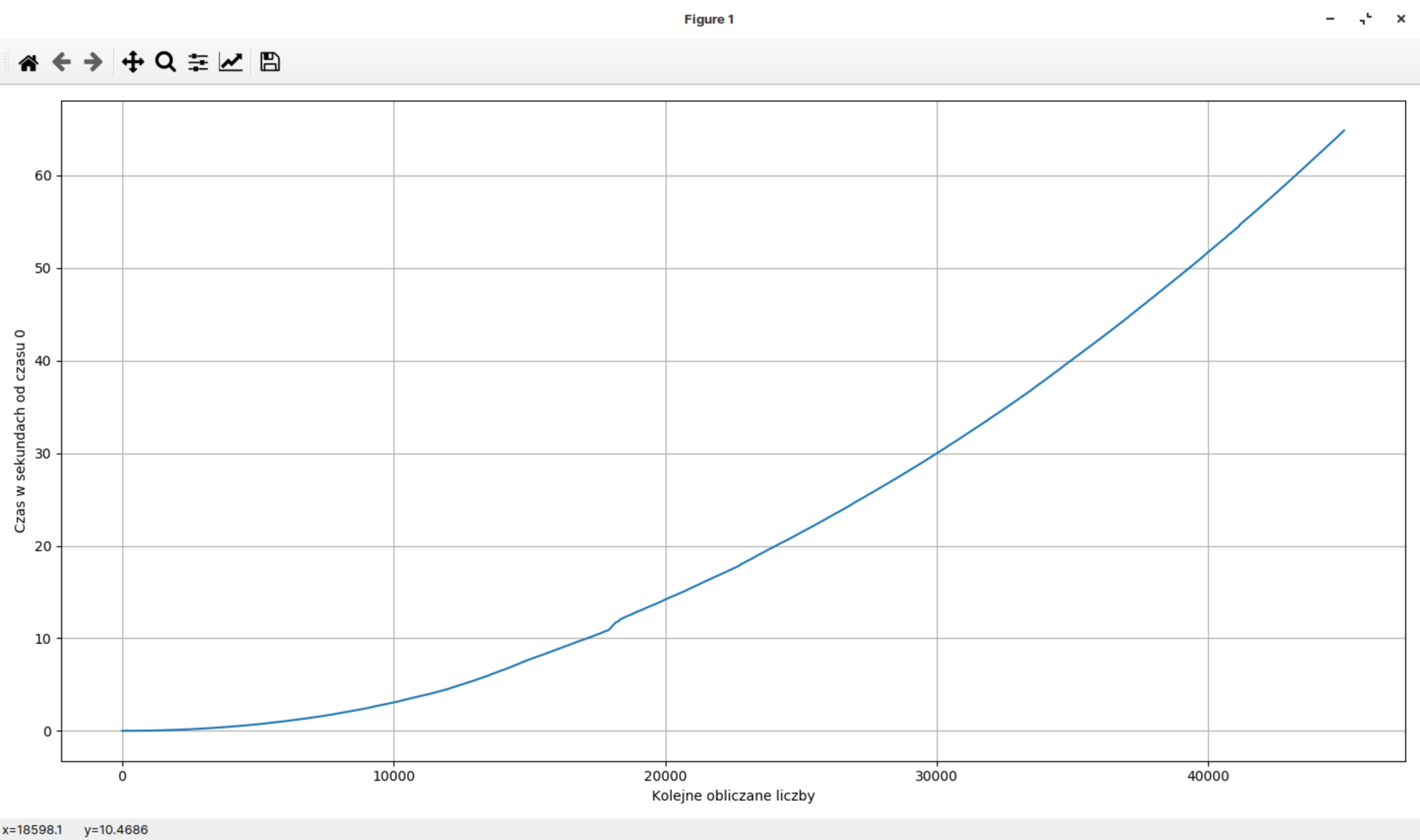
Możemy zauważyć, jak długo trwa wyszukiwanie ostatniej liczby.
Słownik
każdy dzielnik danej liczby, który jest od niej mniejszy
biblioteka służąca do przedstawienia obrazów złożonych z punktów o współrzędnych x oraz y (wykresów, histogramów, rozkładów itp.); moduł matplotlib nie jest dostępny w standardowej instalacji języka Python -należy go zainstalować, korzystając z mechanizmu pip