Punkty szczególne w trójkącie równobocznym

Wiemy, że w każdym trójkącie wysokościwysokość trójkątawysokości przecinają się w jednym punkcie, zwanym ortocentrum trójkątaortocentrum trójkątaortocentrum trójkąta. Ten punkt jest jednym z tzw. punktów szczególnych trójkąta. Innym punktem szczególnym jest środek ciężkości – pojęcie znane lepiej adeptom fizyki – w trójkącie jest to punkt przecięcia trzech jego środkowychśrodkowa w trójkącieśrodkowych. Wreszcie wspomnieć należy punkty szczególne, które są przedmiotem dzisiejszej lekcji – to środek okręgu opisanego na trójkącie, czyli punkt przecięcia symetralnych boków trójkąta oraz środek okręgu wpisanego w trójkąt, czyli punkt przecięcia dwusiecznych kątów wewnętrznych trójkąta.

Rlzb12MB5g6Rn

Ilustracja przedstawia trójkąt ABC. Zaznaczono na nim wysokości, środkowe, dwusieczne oraz symetralne. Wysokości h indeks dolny A koniec indeksu, h indeks dolny B koniec indeksu , h indeks dolny C koniec indeksu przecinają się w punkcie H, środkowe , s indeks dolny B koniec indeksu, s indeks dolny C koniec indeksu przecinają się w punkcie S, dwusieczne d indeks dolny A koniec indeksu, d indeks dolny B koniec indeksu, d indeks dolny C koniec indeksu przecinają się w punkcie I a symetralne s indeks dolny AB koniec indeksu, s indeks dolny BC koniec indeksu, s indeks dolny AC koniec indeksu przecinają się w punkcie O.

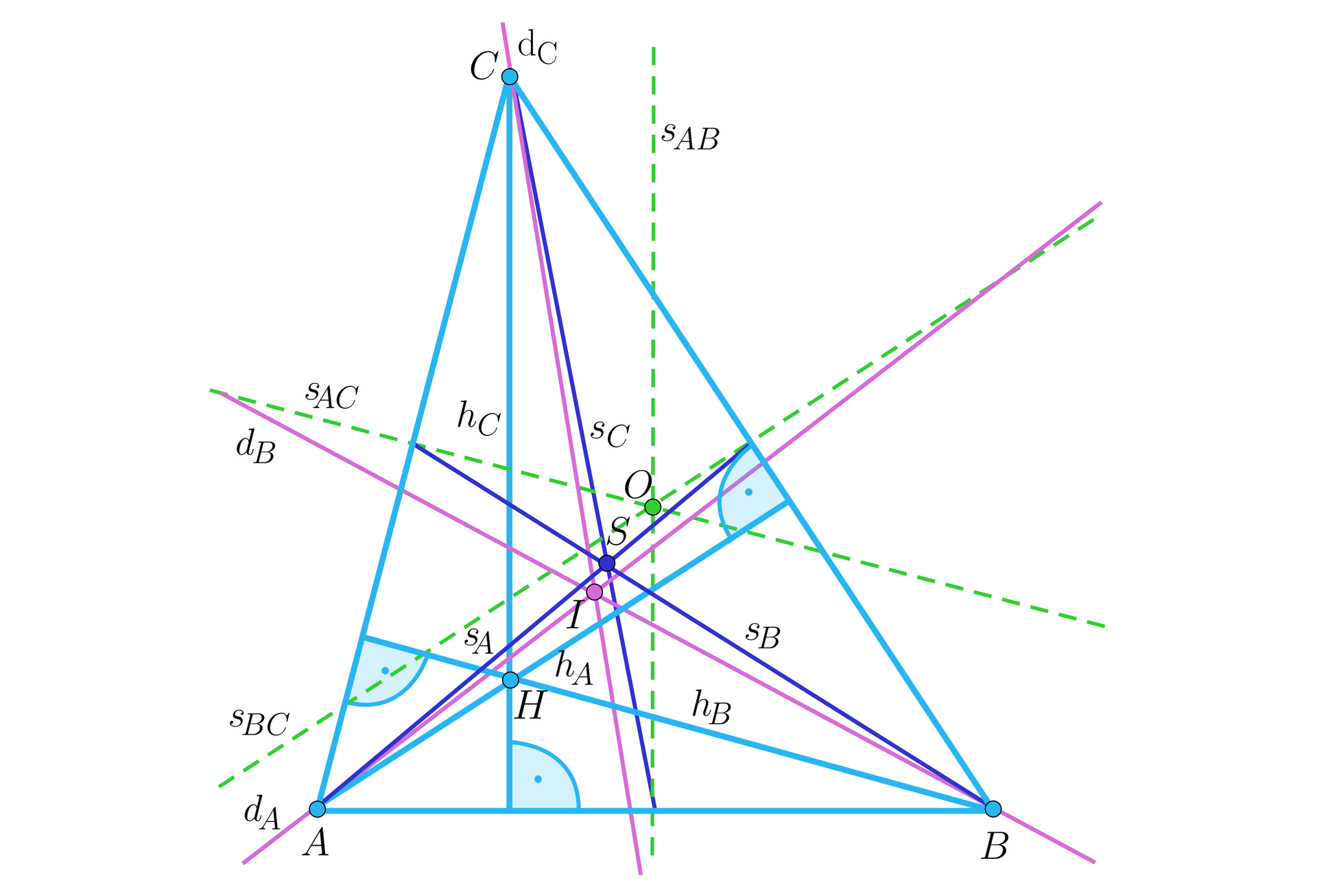
Na powyższym rysunku wysokości $h_A$, $h_B$, $h_C$ przecinają się w punkcie $H$, środkowe $s_A$, $s_B$, $s_C$ przecinają się w punkcie $S$, dwusieczne $d_A$, $d_B$, $d_C$ przecinają się w punkcie $I$ a symetralne $s_{AB}$, $s_{BC}$, $s_{AC}$ przecinają się w punkcie $O$. Nie sposób nie zauważyć, że jednoczesne poprowadzenie prostych i odcinków, wyznaczających poszczególne punkty szczególne, utrudnia dostrzeżenie ewentualnych zależności między obiektami.

Oczywiście znacznie łatwiej ewentualne zależności dostrzec w trójkącie równobocznym, ale wtedy przestaje to być przesłanką do zadawania pytań, bo symetralne boków są jednocześnie dwusiecznymi kątów wewnętrznych trójkąta i zawierają się w nich wysokości i środkowe trójkąta równobocznego, co oznacza, że ortocentrum jest środkiem ciężkości i środkiem okręgów opisanego i wpisanego w ten trójkąt.

Oznaczmy przez $H$ jego ortocentrum, a przez $A_1$, $B_1$, $C_1$ odpowiednie spodki wysokości trójkąta równobocznego $ABC$, jak na rysunku.

R5ZQLD2G9sR2f

Ilustracja przedstawia okrąg do którego wpisano trójkąt ABC. Zaznaczono na nim wysokości w postaci odcinków A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Spotykają się one w punkcie P. W ten trójkąt wpisano okrąg o promieniu r. o środku w punkcie H.

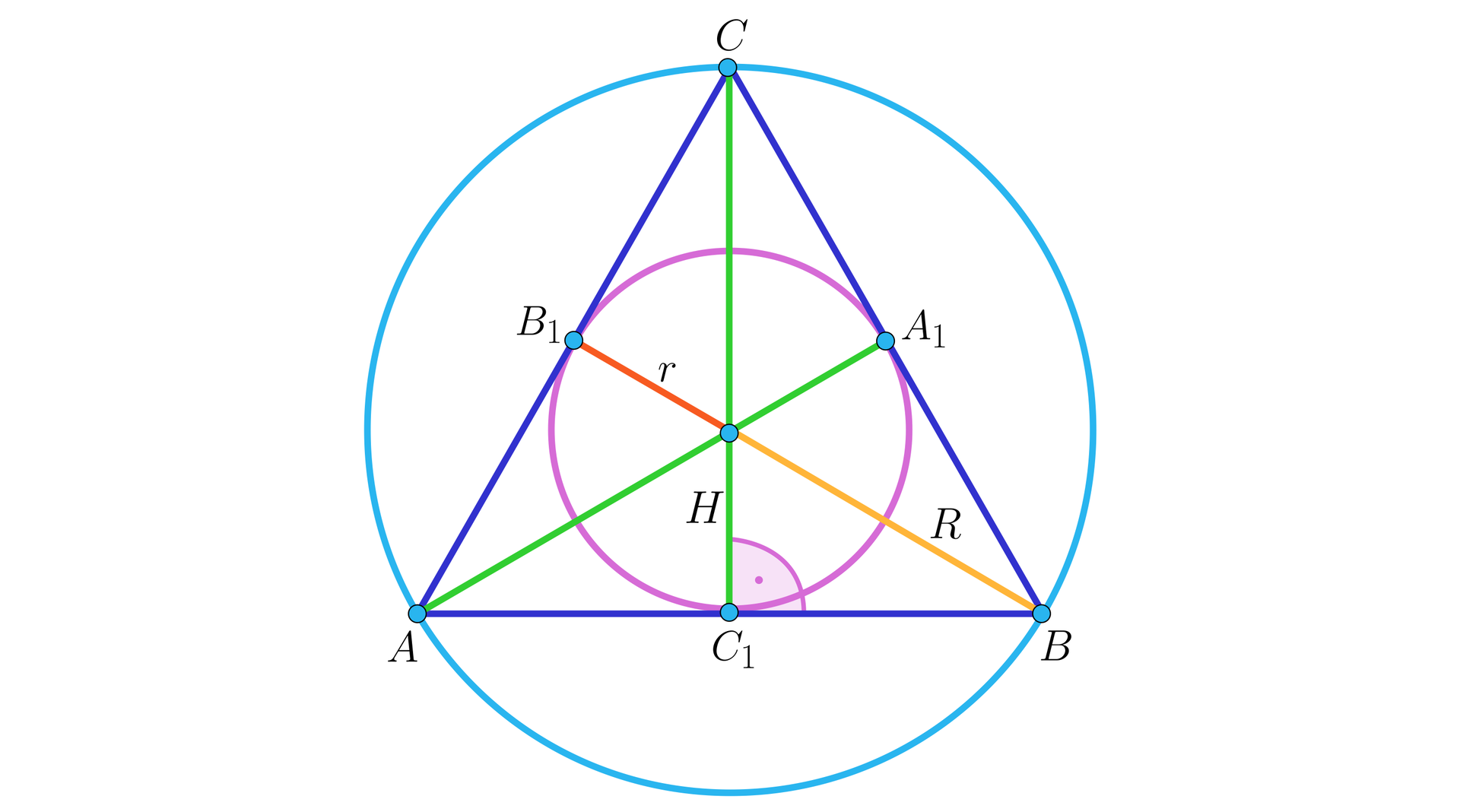
Wtedy mamy oczywiście $\left|H{A}_1\right|=\left|H{B}_1\right|=\left|H{C}_1\right|=r$, gdzie $r$ jest promieniem okręgu wpisanego w ten trójkąt oraz $\left|HA\right|=\left|HB\right|=\left|HC\right|=R$, gdzie $R$ jest promieniem okręgu opisanego na tym trójkącie. Oczywiście $\left|HA\right|=2\left|H{A}_1\right|$, co jest w szczególności konsekwencją twierdzenia o środkowych w trójkącie (dowolnym), które przecinają się w stosunku $2:1$. Naturalnie ten sam wniosek można wyciągnąć, z faktu, że $\sin 30°=\frac{1}{2}=\frac{\left|H{C}_1\right|}{\left|HA\right|}=\frac{\left|H{A}_1\right|}{\left|HA\right|}$.

Prawdziwe jest zatem poniższe twierdzenie.

Przykład 2

Odległość prostej przechodzącej przez środki dwóch boków trójkąta równobocznego od jego ortocentrum jest równa $\sqrt{3}$. Wyznaczymy długość $a$ boku tego trójkąta.

Rozwiązanie:

R1TErrdzXEbj0

Ilustracja przedstawia trójkąt ABC. Zaznaczono wysokość trójkąta. Przez środki ramion trójkąta przechodzi prosta. Z punktu A i B poprowadzono dwie półproste przecinające się w punkcie H.

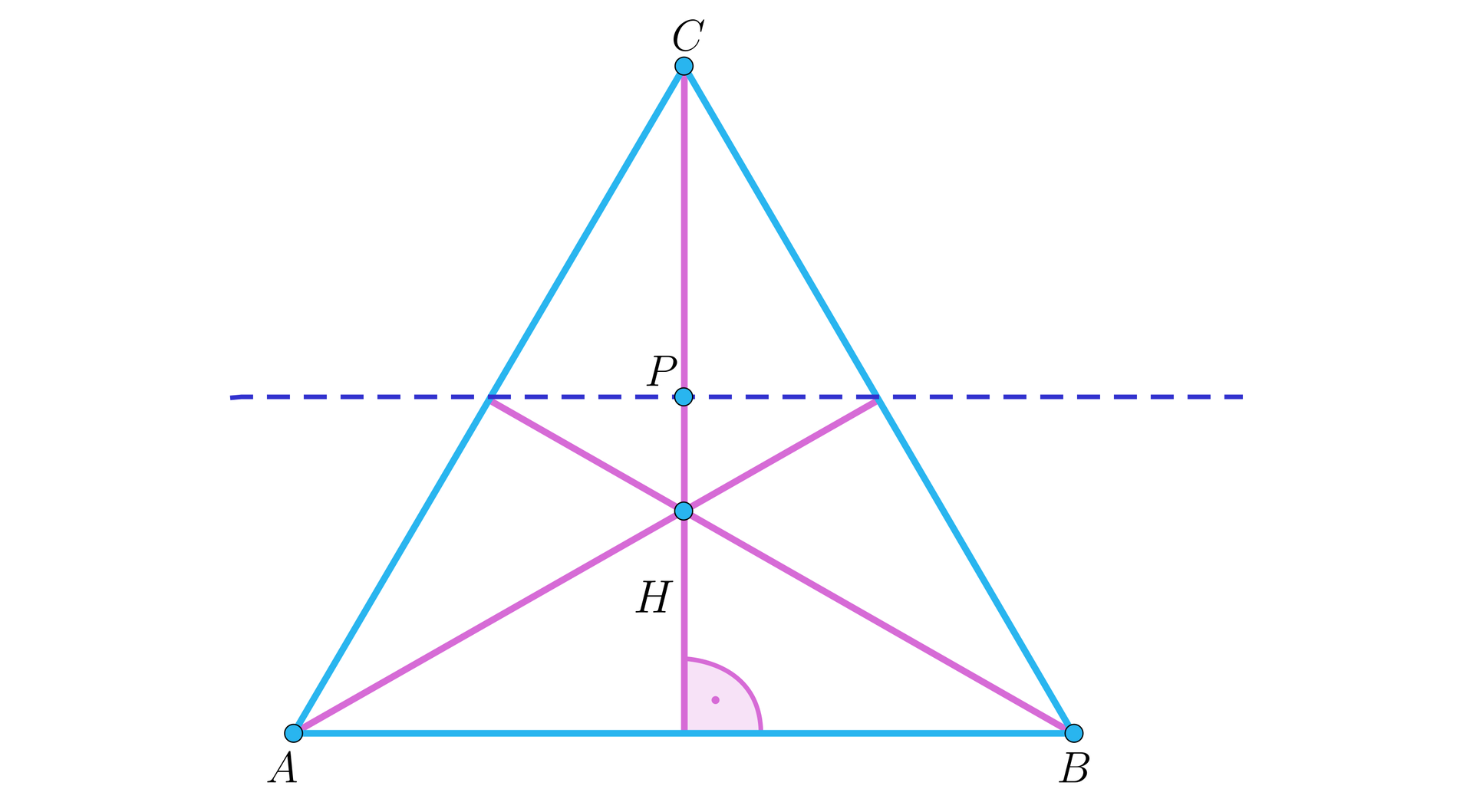
Na wstępie zauważmy, że prosta ta dzieli wysokość trójkąta na połowę. Zatem $\sqrt{3}=\left|PH\right|=\frac{1}{2}h-\frac{1}{3}h=\frac{1}{6}h$. Stąd $h=6\sqrt{3}$. Bok trójkąta jest więc równy:

$a=\frac{2}{\sqrt{3}}h=\frac{2}{\sqrt{3}}·6\sqrt{3}=12$.

Stosunek długości promienia okręgu opisanego na trójkącie do długości promienia okręgu wpisanego w dany trójkąt

Relacja między okręgami w trójkącie równobocznym, w szczególności położenie środków i stosunek długości promieni charakteryzują trójkąt równoboczny. Do takiego wniosku można dojść analizując twierdzenie Eulera i tzw. nierówność Eulera, która jest prostą konsekwencją tego twierdzenia. Przytoczymy tu wspomniane twierdzenie bez dowodu, bowiem dotyczy ono szerszej klasy trójkątów.

Nierówność Eulera

Oczywiście $d^2\ge 0$, czyli $R^2-2Rr\ge 0$. Prowadzi to do nierówności $R\ge 2r$, gdzie równość zachodzi tylko wtedy, gdy $d=0$.
Widać więc, że dla trójkąta, w którym środki okręgów wpisanego i opisanego się pokrywają, stosunek długości promieni okręgów wpisanego i opisanego jest równy $2$. Tym samym taki stosunek jest warunkiem koniecznym i wystarczającym, by trójkąt był równoboczny.

Okręgi opisane na trójkątach równobocznych w optymalizacji

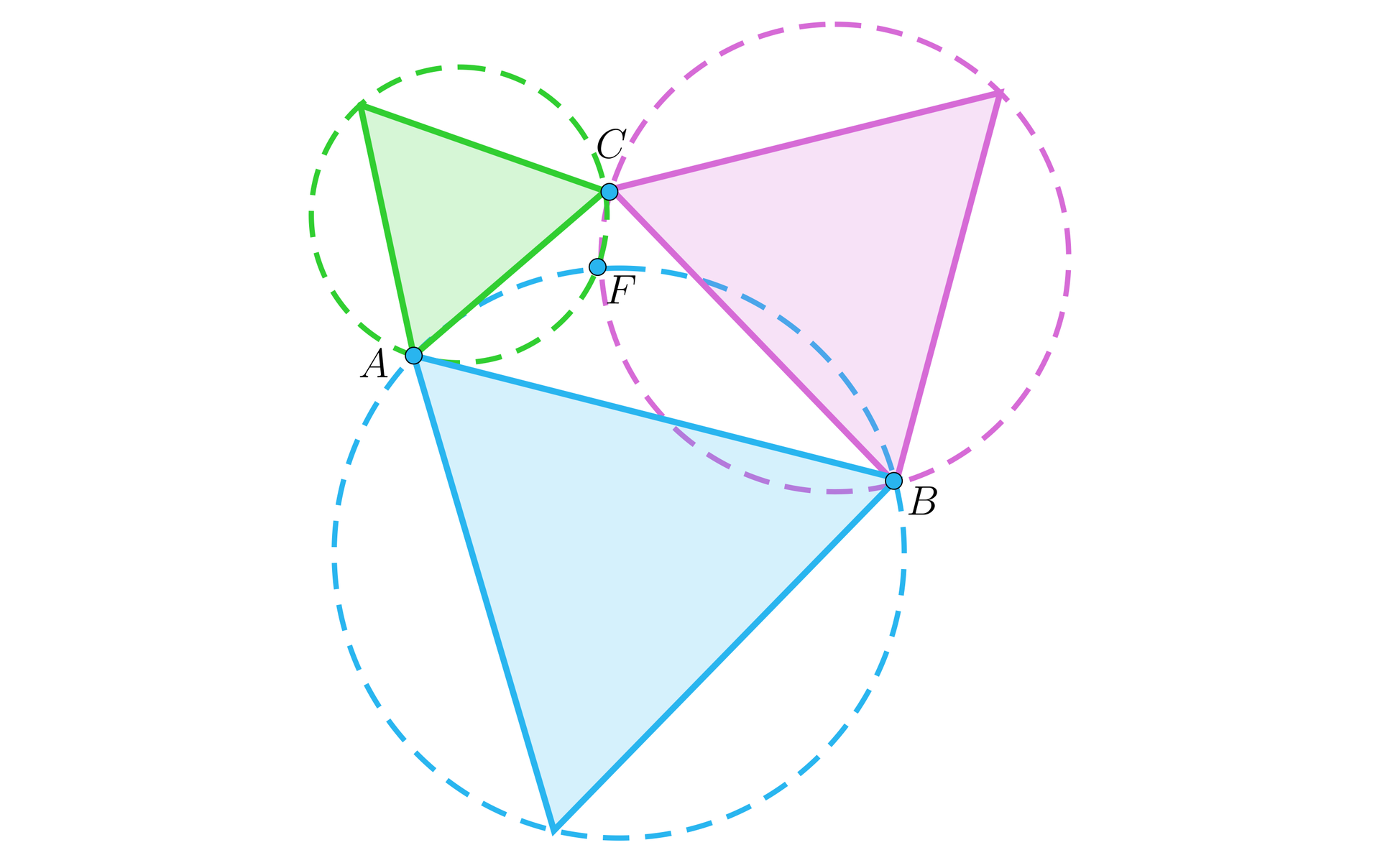
Na koniec przywołamy zagadnienie zwane „okręgami Torricellego”, które stanowi rozwiązanie problemu postawionego przez P. Fermata: mając dane na płaszczyźnie trzy punkty, znajdź czwarty, taki, że suma jego odległości od trzech punktów danych osiąga minimum. Evangelista Torricielli wykazał, że jeśli oznaczymy dane punkty jako $A$, $B$, $C$, następnie zbudujemy trójkąty równoboczne o bokach $AB$, $AC$, $BC$ leżące na zewnątrz trójkąta $ABC$, jak na poniższym rysunku, to okręgi opisane na tych trójkątach przecinają się w jednym punkcie. Punkt ten, zwany punktem Fermata lub punktem Torricellego – Fermata, jest rozwiązaniem postawionego zagadnienia.

RZ5Z0xsaqwyqh

Ilustracja przedstawia punkty ABC, z których zbudujemy trójkąty równoboczne o bokach AB, AC, BC leżące na zewnątrz trójkąta ABC. Opisano okręgi na tych trójkątach.

Słownik