Wyznaczymy wzór funkcji $f\left(x\right)=\frac{a}{x}$ wiedząc, że do jej wykresu należy punkt o współrzędnych $A=\left(-2;5\right)$.

Rozwiązanie

Do wzoru funkcji $f\left(x\right)=\frac{a}{x}$ wstawiamy współrzędne punktu $A=\left(-2;5\right)$.

$5=\frac{a}{-2}$
$a=-10$

czyli wzór funkcji to $f\left(x\right)=\frac{-10}{x}$.

Wyznaczymy wszystkie punkty kratowepunkt kratowypunkty kratowe należące do wykresu funkcji $f\left(x\right)=\frac{a}{x}$ przechodzącego przez punkt $B=\left(3\sqrt{2};3\sqrt{2}\right)$.

Rozwiązanie

Zauważmy, że wzór funkcji $f\left(x\right)=\frac{a}{x}$ można zapisać również w postaci $y=\frac{a}{x}$.

Mnożąc obustronnie przez $x$:

$y=\frac{a}{x}$
$xy=a$

czyli w naszym przypadku:

$a=3\sqrt{2}·3\sqrt{2}=18$

Aby wyznaczyć wszystkie punkty kratowe należące do wykresu funkcji należy wyznaczyć wszystkie pary liczb całkowitych, dla których $x·y=18$.

Odpowiedź: Są to punkty: $\left(1;18\right)$, $\left(2;9\right)$, $\left(3;6\right)$, $\left(6;3\right)$, $\left(9;2\right)$, $\left(18;1\right)$ oraz $\left(-1;-18\right)$, $\left(-2;-9\right)$, $\left(-3;-6\right)$, $\left(-6;-3\right)$, $\left(-9;-2\right)$, $\left(-18;-1\right)$.

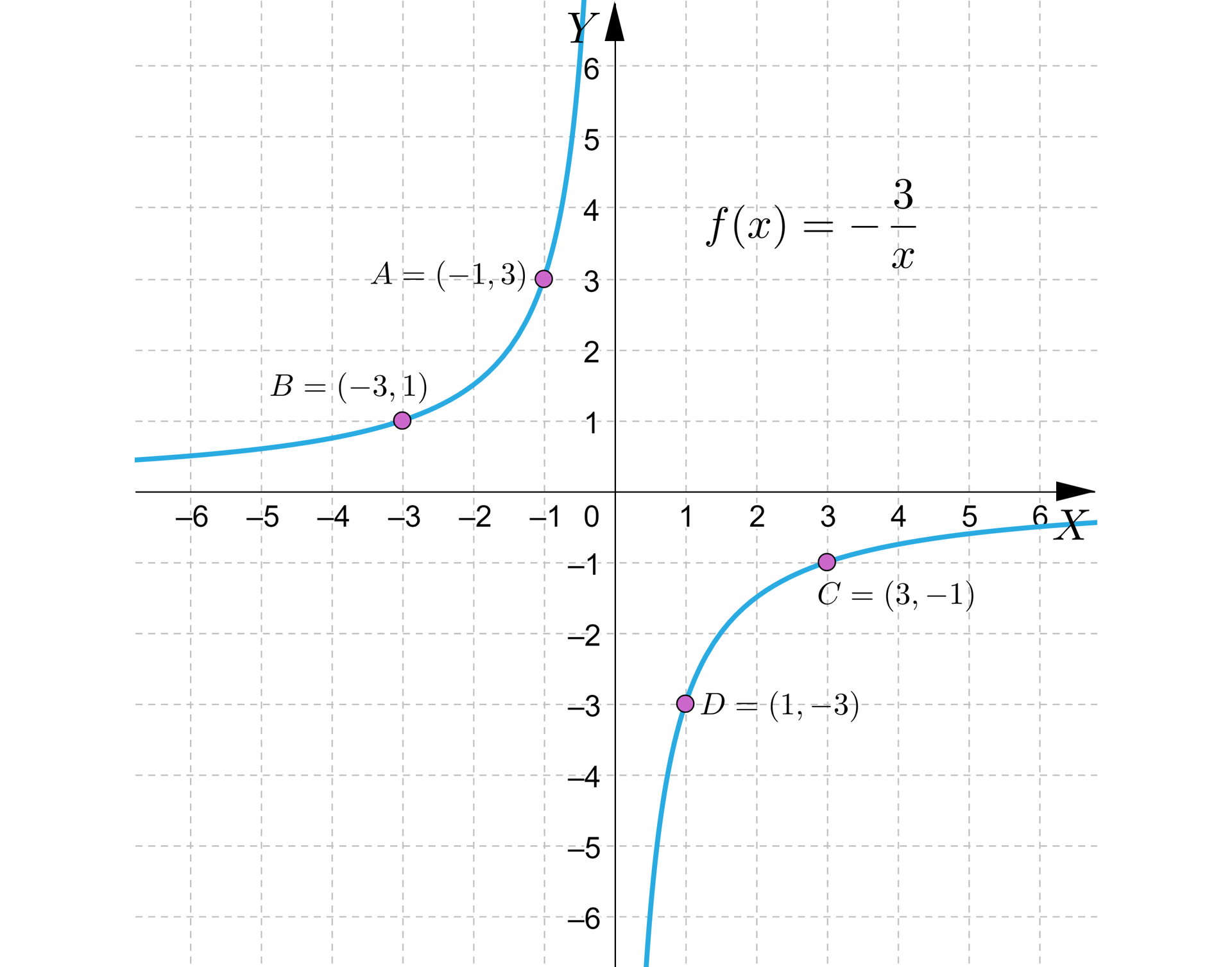
Narysujemy wykres funkcji $f\left(x\right)=\frac{a}{x}$ wiedząc, że do jej wykresu należy punkt $C=\left(-\sqrt{3};\sqrt{3}\right)$.

Rozwiązanie

Podobnie jak w przykładzie 2 zauważamy, że wzór funkcji $f\left(x\right)=\frac{a}{x}$ można zapisać również w postaci $y=\frac{a}{x}$.

Mnożąc obustronnie przez $x$:

$y=\frac{a}{x}$
$xy=a$

czyli w naszym przypadku:

$\left(-\sqrt{3}\right)·\sqrt{3}=\left(-3\right)$

Aby wyznaczyć inne punkty kratowe należące do wykresu funkcji, należy wyznaczyć pary liczb całkowitych, dla których $x·y=\left(-3\right)$. Są to punkty $\left(1;-3\right)$, $\left(-1;3\right)$, $\left(-3;1\right)$, $\left(3;-1\right)$. Teraz sporządzamy wykres funkcji.

R1ZDeIjvR0mBJ

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus sześciu do sześciu oraz pionową osią $Y$ od minus sześciu do sześciu. Na płaszczyźnie narysowano wykres funkcji, który stanowi hiperbola. Gałęzie hiperboli leżą w drugiej i czwartej ćwiartce układu współrzędnych. Czerwonymi kropkami zaznaczono należące do wykresu punkty $A=\left(-1;3\right)$, $B=\left(-3;1\right)$, $C=\left(3;-1\right)$ oraz $D=\left(1;-3\right)$.

Wyznaczymy wzór funkcji $f\left(x\right)=\frac{a}{x}$, $a\ne 0$, jeśli wiadomo, że $f\left(\sqrt{7}\right)-f\left(\sqrt{7}+1\right)=f\left(\sqrt{7}\right)·f\left(\sqrt{7}+1\right)$.

Rozwiązanie

$f\left(\sqrt{7}\right)-f\left(\sqrt{7}+1\right)=f\left(\sqrt{7}\right)·f\left(\sqrt{7}+1\right)$

$\frac{a}{\sqrt{7}}-\frac{a}{\sqrt{7}+1}=\frac{a}{\sqrt{7}}·\frac{a}{\sqrt{7}+1}$

$\frac{a\left(\sqrt{7}+1\right)}{\sqrt{7}\left(\sqrt{7}+1\right)}-\frac{a\sqrt{7}}{\sqrt{7}\left(\sqrt{7}+1\right)}=\frac{a^2}{\sqrt{7}\left(\sqrt{7}+1\right)}$

$\frac{a\sqrt{7}+a-a\sqrt{7}}{\sqrt{7}\left(\sqrt{7}+1\right)}=\frac{a^2}{\sqrt{7}\left(\sqrt{7}+1\right)}$

$a=a^2$

$a-a^2=0$
$a\left(1-a\right)=0$
$a=0\vee a=1$

ponieważ $a\ne 0$, czyli równość zachodzi dla $a=1$.

Odpowiedź: $f\left(x\right)=\frac{1}{x}$

Prosta o równaniu $y=x$ przecina hiperbolę o równaniu $y=\frac{a}{x}$, $x\ne 0$, w dwóch punktach oddalonych od siebie o $4$. Wyznaczymy równanie hiperboli.

Rozwiązanie

Ponieważ środkiem symetrii hiperboli o równaniu $y=\frac{a}{x}$, $x\ne 0$, jest punkt $\left(0,0\right)$, to punkty przecięcia tej hiperboli z prostą o równaniu $y=x$ mają współrzędne: $A=\left(x,x\right)$ oraz $A\text{'}=\left(-x,-x\right)$. Zatem odległość tych punktów jest równa: $\left|AA\text{'}\right|=\sqrt{{\left(x+x\right)}^2+{\left(x+x\right)}^2}$.

Stąd mamy: $\sqrt{8x^2}=4$, co daje: $2\sqrt{2}\left|x\right|=4$. Zatem $x=\sqrt{2}$ lub $x=-\sqrt{2}$.

Wyznaczamy $a$:

$\frac{a}{\sqrt{2}}=\sqrt{2}$, czyli: $a=2$.

Zatem równanie hiperboli ma postać: $y=\frac{2}{x}$.

wielkości $x$ oraz $y$ są odwrotnie proporcjonalne wtedy i tylko wtedy, gdy ich iloczyn jest wielkością stałą i różną od zera

punkt, którego współrzędne w układzie kartezjańskim (prostokątnym) są liczbami całkowitymi