Przeczytaj
Zdefiniujmy najpierw, kiedy prosta jest równoległa do płaszczyzny.
Dana jest płaszczyzna oraz proste i . Mówimy, że prosta i płaszczyzna są równoległe, gdy nie mają punktów wspólnych (płaszczyzna i prosta ), lub prosta zawarta jest w tej płaszczyźnie (płaszczyzna i prosta ).
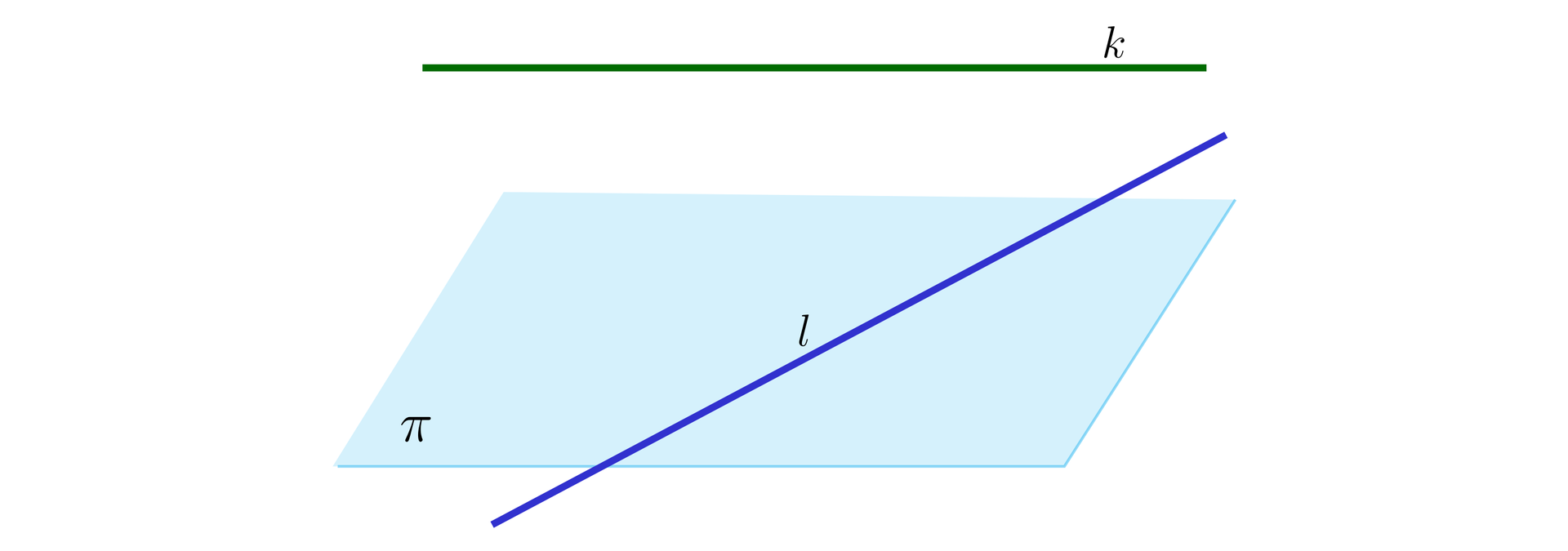
Jeżeli prosta jest równoległa do płaszczyzny, wówczas możemy wyznaczyć odległośćodległość między tą prostą a płaszczyzną. Gdy prosta jest zawarta w danej płaszczyźnie, to odległość tej prostej od płaszczyzny wynosi .
Dany jest prostopadłościan . Wskażemy wszystkie proste, które zawierają krawędzie prostopadłościanu i są równoległe do płaszczyzny .
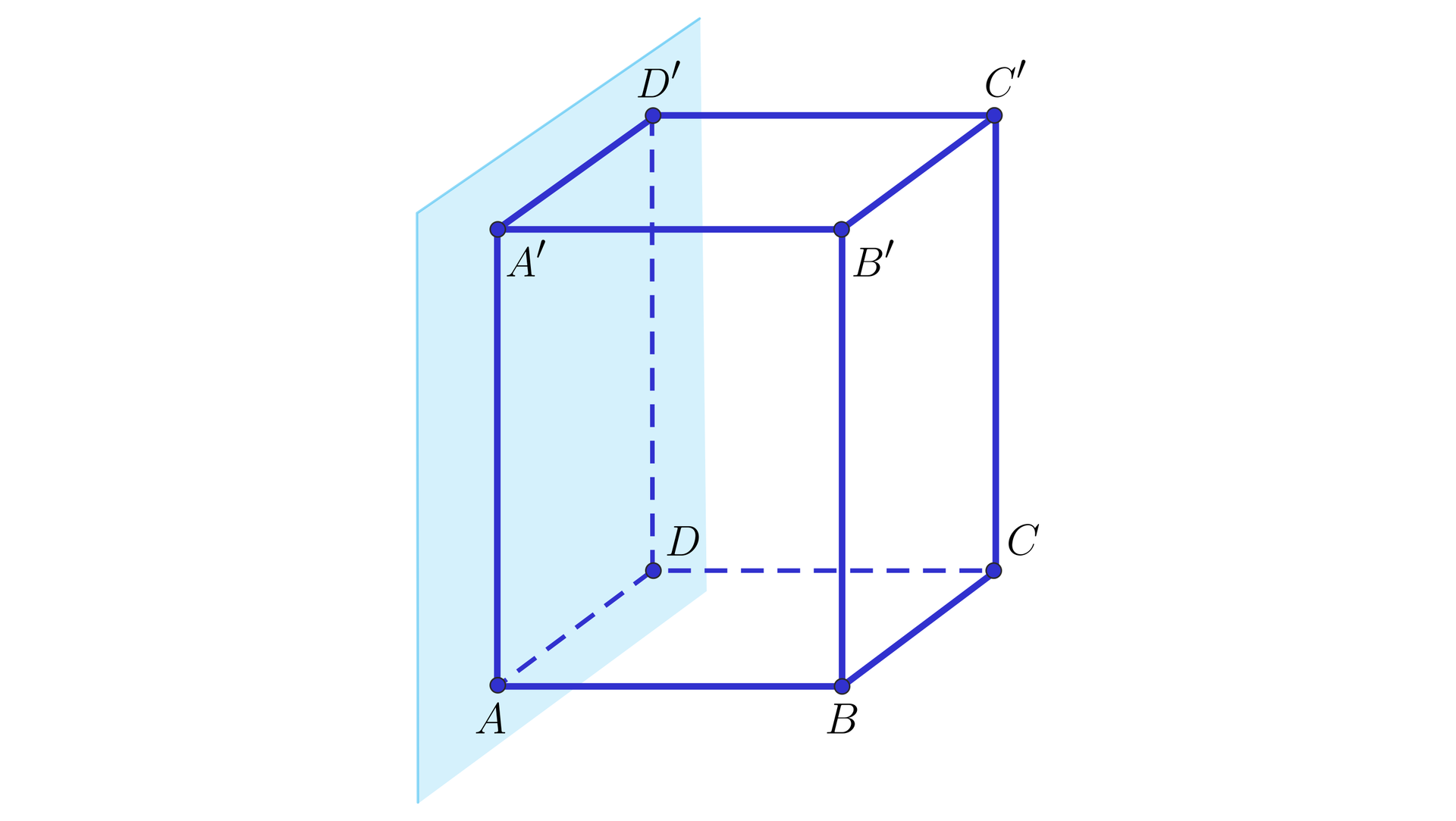
Rozwiązanie:
Jeżeli wykorzystamy definicję prostej równoległej do płaszczyzny, prostymi równoległymi do płaszczyzny , zawierającymi krawędzie prostopadłościanu są proste:
zawarte w tej płaszczyźnie: , , , ,
nie należące do tej płaszczyzny: , , , .
Dany jest prostopadłościan . Obliczymy odległości prostych zawierających krawędzie tego prostopadłościanu, równoległych do płaszczyzny , nienależących do tej płaszczyzny, jeżeli krawędzie prostopadłościanu mają długości: , , .
Rozwiązanie
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na rysunku.
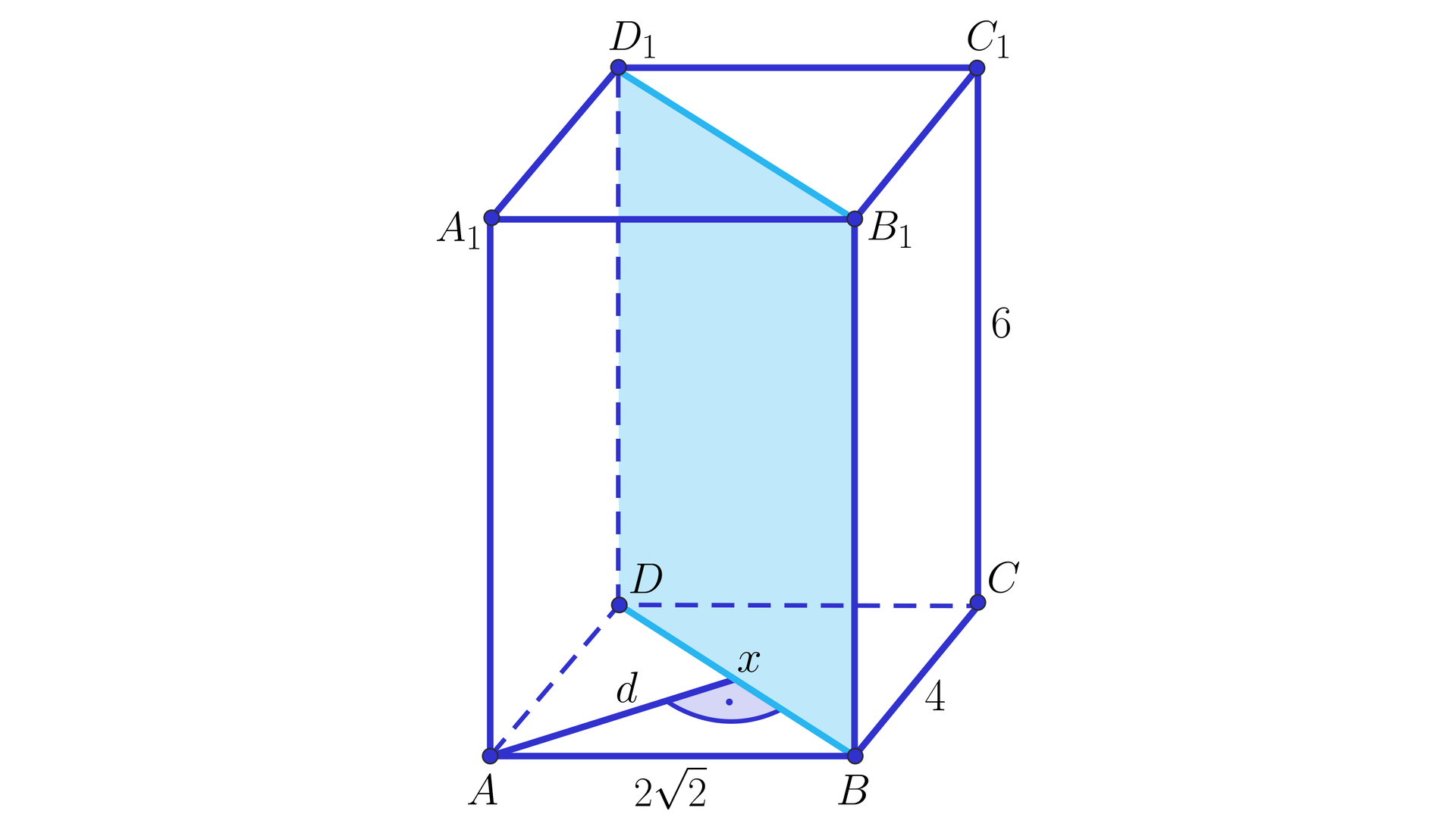
Zauważmy, że tylko proste oraz zawierają krawędzie tego prostopadłościanu, które są równoległe do płaszczyzny i nie należą do tej płaszczyzny.
Odległości tych prostych od płaszczyzny są takie same. Niech będzie szukaną odległością.
Wówczas:
.
Zatem .
Pole trójkąta jest równe:
oraz
.
Wobec tego:
.
Dany jest graniastosłup prawidłowy trójkątny , jak na poniższym rysunku oraz płaszczyzna, przechodząca przez środki krawędzi , , , graniastosłupa.
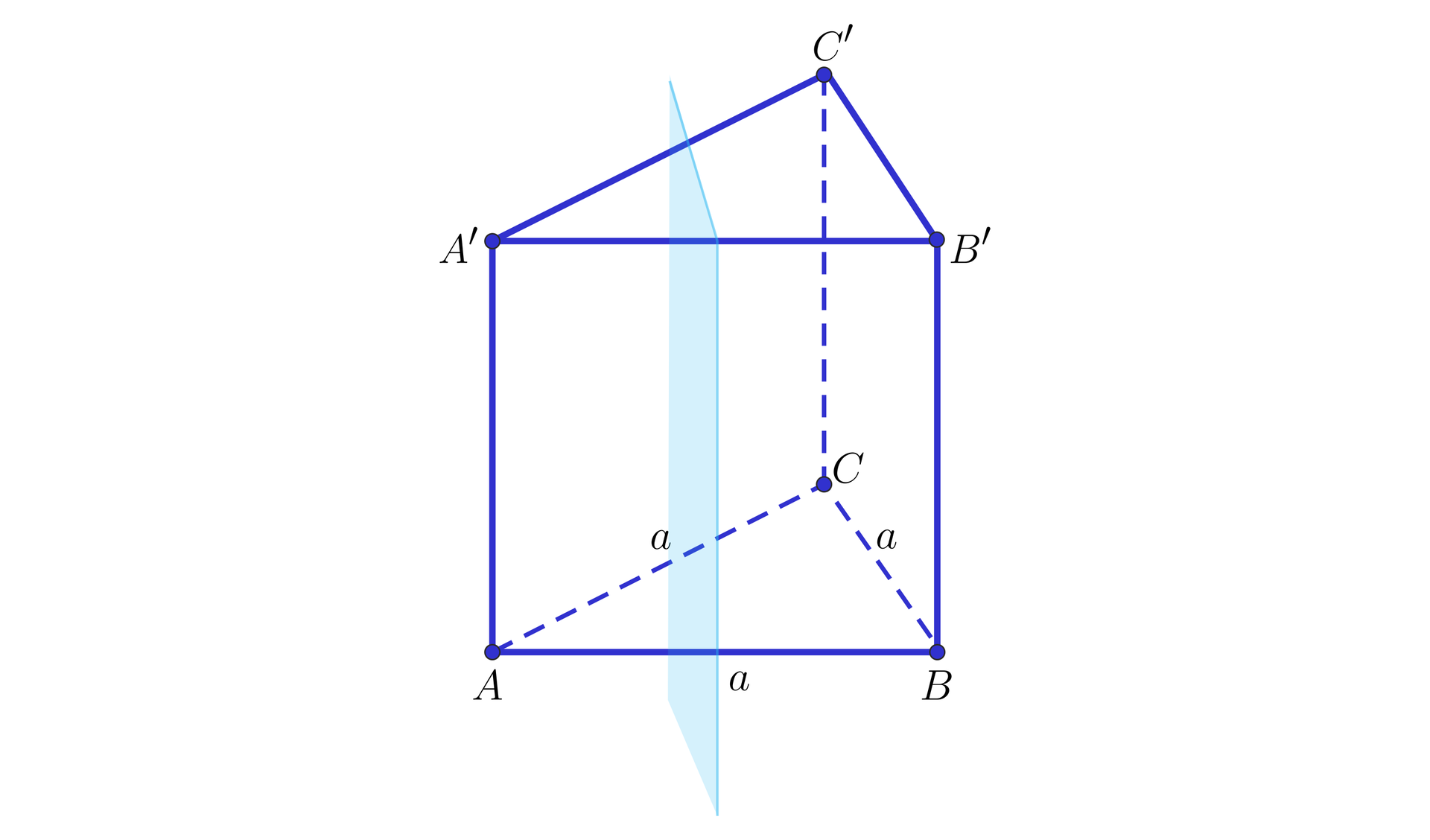
Wskażemy proste zawierające krawędzie graniastosłupa, które są równoległe do danej płaszczyzny, a następnie obliczymy odległości tych prostych od płaszczyzny, jeżeli długość krawędzi podstawy graniastosłupa jest równa .
Rozwiązanie
Proste równoległe do podanej płaszczyzny, zawierające krawędzie graniastosłupa, to: , oraz .
Zauważmy, że odległości tych prostych od podanej płaszczyzny są równe. Niech będzie szukaną odległością.
Rozpatrzmy trójkąt równoboczny, jak na poniższym rysunku:
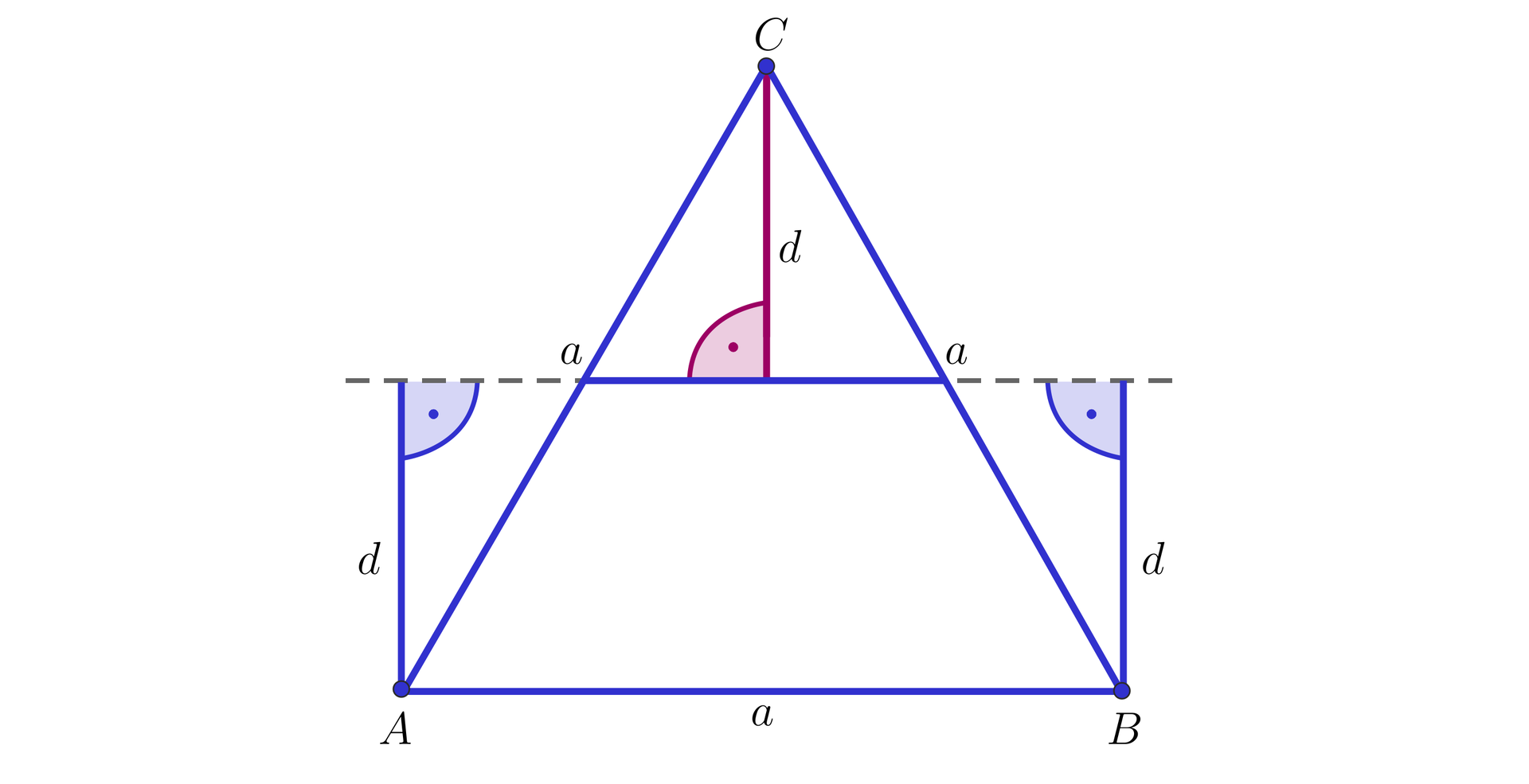
Szukana odległość jest równa połowie długości wysokości omawianego trójkąta.
Zatem .
Narzędzia użyte w poniższych przykładach wykraczają poza wymagania podstawy programowej, jednak są ich ciekawym uzupełnieniem.
Istnieje również definicja prostej równoległej do płaszczyzny, w której wymienione figury przedstawia się za pomocą wektorów.
Niech prosta będzie określona przez wektor do niej równoległy (wektor kierunkowy), a płaszczyzna przez wektor do niej prostopadły (wektor normalny).
Mówimy, że prosta jest równoległa do płaszczyzny wtedy, gdy wektory normalny i kierunkowy są do siebie prostopadłe, czyli ich iloczyn skalarnyiloczyn skalarny jest równy .
Iloczyn skalarny wektorów i obliczamy ze wzoru:
Sprawdzimy, czy prosta określona przez wektor kierunkowy oraz płaszczyzna o wektorze normalnym są do siebie równoległe.
Rozwiązanie
Obliczamy iloczyn skalarnyiloczyn skalarny wektorów i .
Zatem
.
Ponieważ , zatem prosta i płaszczyzna nie są równoległe.
Wyznaczymy dla jakich wartości parametru prosta określona przez wektor kierunkowy oraz płaszczyzna określona przez wektor normalny są równoległe.
Rozwiązanie
Do wyznaczenia wartości parametru sprawdzimy, kiedy zachodzi warunek .
Wobec tego:
.
Rozwiązujemy równanie .
Zatem .
Słownik
długość najkrótszej krzywej łączącej dane punkty
funkcja przyporządkowująca dwóm wektorom przestrzeni liniowej pewną wartość liczbową