Pole siatki czworościanu foremnego wynosi $32\sqrt{3} {\mathrm{cm}}^2$. Znajdź długość krawędzi tego czworościanu.

Rozwiązanie:

Pole siatki czworościanu $P=32\sqrt{3} {\mathrm{cm}}^2$.

Na siatkęsiatka czworościanusiatkę składają się $4$ trójkąty równoboczne, stąd pole jednej ściany czworościanu foremnego wynosi $P_{ś}=8\sqrt{3} {\mathrm{cm}}^2$.

Skorzystamy ze wzoru na pole trójkąta równobocznego: $P_{ś}=\frac{a^2\sqrt{3}}{4}=8\sqrt{3}$.

Długość krawędzi czworościanu wynosi zatem $a=\sqrt{32}=4\sqrt{2} \mathrm{cm}$.

Wysokość trójkąta równobocznego stanowiącego siatkę czworościanu foremnego ma długość $8\sqrt{3} \mathrm{cm}$. Wyznacz pole podstawy czworościanu foremnego.

Rozwiązanie:

Wysokość trójkąta równobocznego stanowiącego siatkę czworościanu foremnego stanowi dwie długości wysokości ściany czworościanu foremnego, trójkąta równobocznego będącego również podstawą czworościanu.

RDiygWeMvQcOv

Na ilustracji przedstawiono siatkę czworościanu, która wygląda następująco. Na każdym boku czerwonego trójkąta równobocznego zbudowano kolejny, niebieski trójkąt równoboczny. Zaznaczono wysokość trójkąta niebieskiego oraz czerwonego, długości obu wysokości oznaczono literą h.

Zatem wysokość podstawy czworościanu wynosi $h=4\sqrt{3} \mathrm{cm}$.

Ponieważ $h=\frac{a\sqrt{3}}{2}=4\sqrt{3}$, to długość boku trójkąta równobocznego $a=8\mathrm{c}\mathrm{m}$.

Zatem pole podstawy czworościanu foremnego $P=\frac{a^2\sqrt{3}}{4}=\frac{8^2}{4}\sqrt{3}=16\sqrt{3}{\mathrm{c}\mathrm{m}}^2$.

Sebastian wykonał z papieru kartonowego model czworościanu foremnego dla swojej siostry Zuzi. Siostrze bardzo spodobała się bryła i poprosiła brata, aby następnego dnia wykonał większy model. Sebastian postanowił zwiększyć długość krawędzi modelu czworościanu o $60\%$. Oblicz, o ile procent zwiększy się pole powierzchni siatki czworościanu, który wykona chłopiec.

Rozwiązanie:

Niech $a$ oznacza długość krawędzi czworościanu mniejszego, a $P_m$ pole siatki tego czworościanu.

Po zwiększeniu długości krawędzi o $60\%$ długość krawędzi czworościanu będzie wynosiła $1,6a$, a jego pole $P_d={\left(1,6\right)}^2{P}_m=2,56P_m$.

Wyznaczmy o ile zwiększy się pole: $P_d-P_m=2,56P_m-P_m=1,56P_m$, czyli pole siatki czworościanu zwiększy się o $\frac{1,56P_m}{P_m}\cdot 100\%=156\%$.

Czworościan foremny wpisano w sześcian o krawędzi długości $a$ tak, że każda krawędź czworościanu jest przekątną ściany tego sześcianu. Wyznacz stosunek pola powierzchni sześcianu do pola powierzchni czworościanu.

Rozwiązanie:

R11rLUZ88AT76

Na ilustracji przedstawiono sześcian o długości krawędzi oznaczonej literą a oraz podstawie dolnej A B C D i górnej E F G H. W sześcian wpisano czworościan foremny, w taki sposób, że wierzchołki A, C, F są wspólne dla obu brył. Przekątne H F, A H, C H, A F, A C, F C stanowią krawędzie czworościanu.

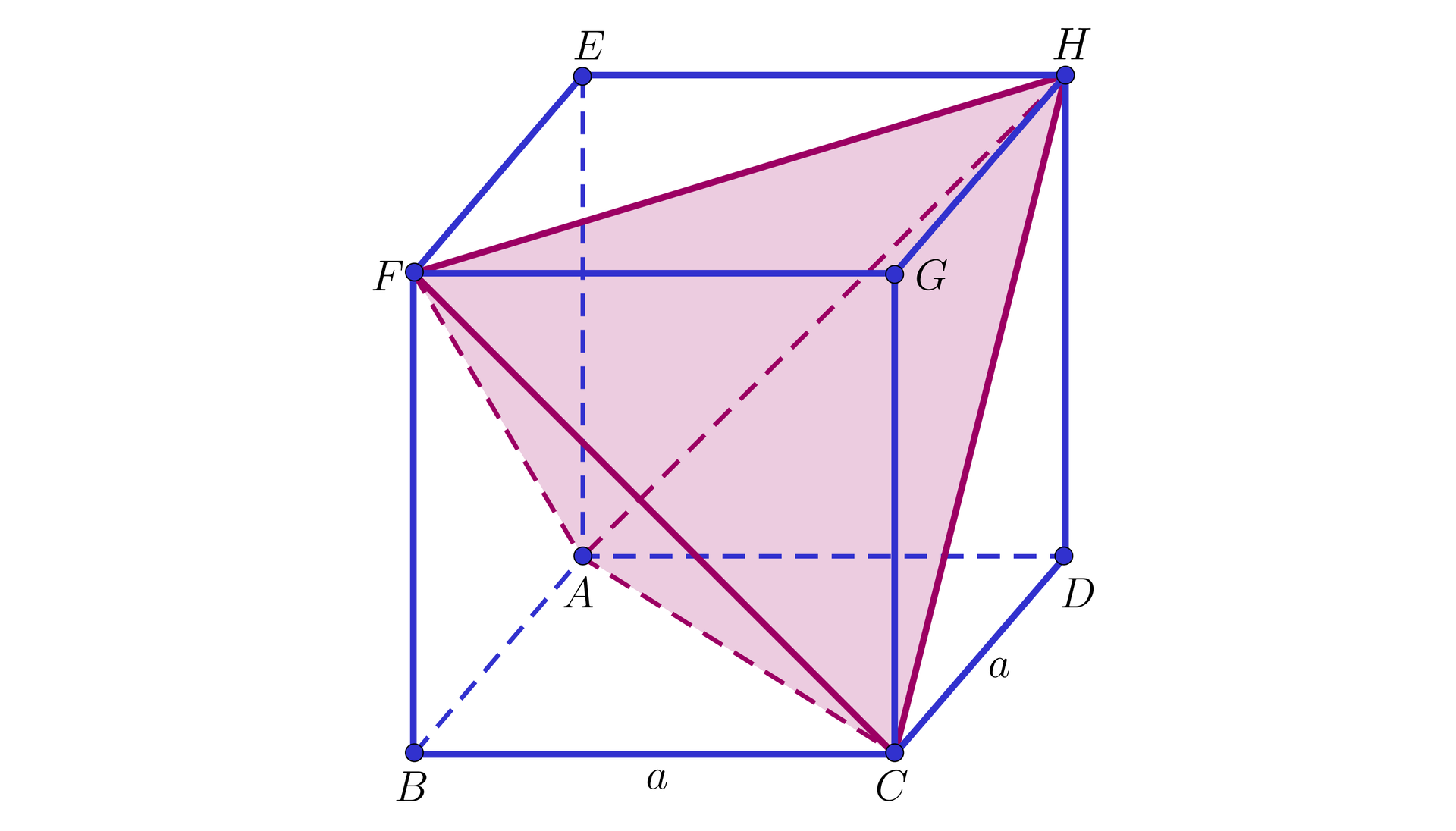
Pole powierzchni sześcianu wynosi $P_{sz}=6a^2$.

Ponieważ krawędź czworościanu jest przekątną ściany sześcianu, to długość krawędzi czworościanu równa jest $d=a\sqrt{2}$.

Pole powierzchni czworościanu foremnego wynosi $P_{cz}=4\frac{d^2\sqrt{3}}{4}={\left(a\sqrt{2}\right)}^2\sqrt{3}=2\sqrt{3}{a}^2$.

Stąd stosunek pola powierzchni sześcianu do pola powierzchni czworościanu foremnego wynosi $\frac{P_{sz}}{P_{cz}}=\frac{6a^2}{2\sqrt{3}{a}^2}=\sqrt{3}$.

Z czterech czworościanów foremnych zbudowano większy czworościan foremny w ten sposób, że na trzech małych czworościanach foremnych postawiono czwarty. Wysokość tak otrzymanej bryły wynosi $4\sqrt{6}$. Wewnętrzne strony pomalowano na kolor zielony, zaś zewnętrzne na kolor niebieski. Podstawa została niepomalowana. Oblicz pole powierzchni pomalowanej na kolor zielony i pole powierzchni pomalowanej na kolor niebieski.

Rozwiązanie:

Ros2FOyJcx4cm

Ilustracja przedstawia czworościan foremny zbudowany z czterech czworościanów foremnych o tych samych, ale mniejszych wymiarach. Na trzech czworościanach postawiono czwarty z nich, tworząc na każdej ścianie czworościanu lukę w kształcie trójkąta równobocznego. Oznacza to, że wnętrze powstałego czworościanu foremnego jest puste. Każdy z mniejszych czworościanów ma wierzchołki znajdujące się po środku krawędzi większego czworościanu lub w wierzchołku jego dolnej podstawy.

Wysokość małego czworościanu stanowi połowę wysokości otrzymanej bryły, czyli $H=2\sqrt{6}$.

Korzystając ze wzoru na wysokość czworościanu foremnegowysokość czworościanu foremnegowysokość czworościanu foremnego $H=\frac{a\sqrt{6}}{3}=2\sqrt{6}$. Stąd $a=6$.

Na kolor zielony pomalowano $4$ ściany, a na kolor niebieski $9$ ścian.

Pole powierzchni jednej ściany wynosi $P=\frac{a^2\sqrt{3}}{4}=\frac{6^2\sqrt{3}}{4}=\frac{36\sqrt{3}}{4}=9\sqrt{3}$.

Otrzymujemy zatem – pole powierzchni pomalowanej na zielono: $4\cdot 9\sqrt{3}=36\sqrt{3}$, zaś pole powierzchni pomalowanej na niebiesko: $9\cdot 9\sqrt{3}=81\sqrt{3}$.

figura płaska, powstająca w wyniku rozcięcia wielościanu wzdłuż pewnych krawędzi i rozłożenia ścian na płaszczyźnie

obliczamy ze wzoru: