Przeczytaj

W przestrzeni rozważamy trzy podstawowe obiekty: punkt, prostą, płaszczyznę. Przez dowolne dwa punkty można poprowadzić dokładnie jedną prostą. Przez dowolne trzy punkty można poprowadzić dokładnie jedną płaszczyznę. Problemy geometrii przestrzennej dają się często rozwiązać jako problemy planimetrii dzięki odpowiedniemu wyborowi płaszczyzny lub przekroju płaszczyznąprzekroju płaszczyzną.

Jeśli dwie płaszczyzny mają punkt wspólny, to częścią wspólną tych płaszczyzn jest prosta zwana krawędzią wspólną tych płaszczyzn. Prosta może mieć jeden punkt wspólny z płaszczyzną i wtedy mówimy, że prosta przebija płaszczyznę. Prosta może leżeć na płaszczyźnie lub nie mieć punktów wspólnych z płaszczyzną.

Aksjomat równoległości (postulat Euklidesa)

Dla prostej $l$ i punktu $B$ nienależącego do niej, istnieje w płaszczyźnie zawierającej prostą $l$ i punkt $B$ dokładnie jedna prosta zawierająca $B$ i niemająca punktów wspólnych z $l$ .

Z aksjomatu równoległości wynika, że jeśli prosta $l$ i punkt $B$ leżą na jednej płaszczyźnie, to istnieje w tej płaszczyźnie dokładnie jedna prosta $l'$ przechodząca przez punkt $B$ i niemająca punktów wspólnych z $l$ . Oznacza to, że prosta $l'$ jest równoległa do prostej $l$ .

R1MsFF8pysz2o

Ilustracja przedstawia płaszczyznę oraz dwie równoległe do siebie proste. Jedna z nich została namalowana linią ciągłą i jest podpisana literą l. Druga z nich została namalowana linią przerywaną i przechodzi przez punkt B leżący na płaszczyźnie.

Zatem jeśli ograniczymy rozważania do jednej płaszczyzny, to możemy korzystać z wszystkich własności prostych równoległych znanych z planimetrii, na przykład, że odległość między prostymi równoległymi jest równa odległości jednej z tych prostych od dowolnego punktu drugiej prostej. Między innymi możemy stosować twierdzenie Talesa i twierdzenie odwrotne do twierdzenia Talesa oraz twierdzenie o prostych równoległych przeciętych trzecią prostą. Zachodzi też własność, że jeżeli dwie proste są równoległe do trzeciej prostej, to są równoległe do siebie.

Przykład 1

Pokażemy, że krawędzie $A B$ i $E F$ sześcianu przedstawionego na rysunku zawarte są w prostych równoległych na płaszczyźnie wyznaczonej przez ścianę $A B F E$ .

RKNJCPWAzdzPc

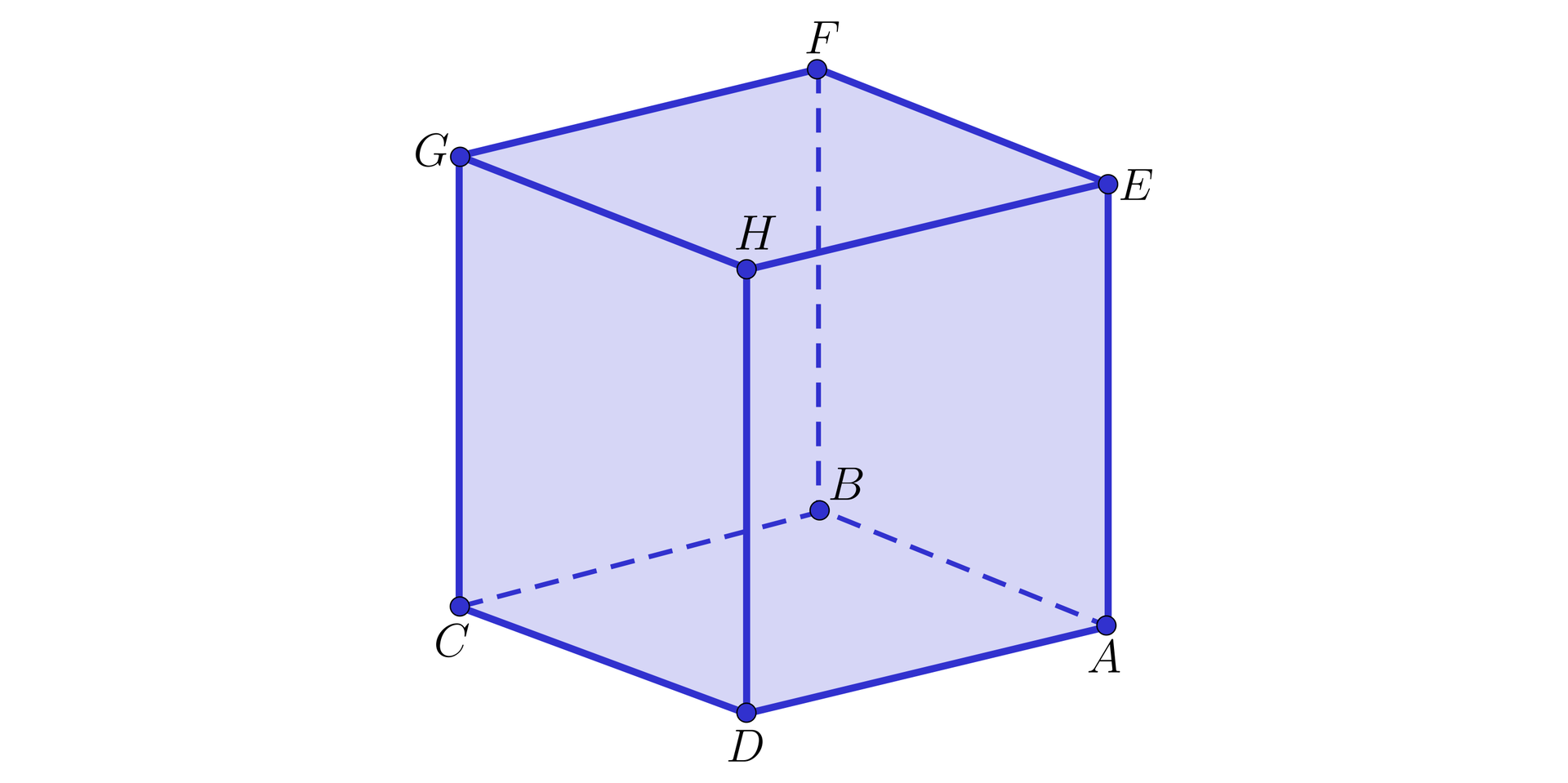
Ilustracja przedstawia sześcian o wierzchołkach A B C D E F G H.

Rozwiązanie

Rzeczywiście, krawędzie $A B$ i $E F$ leżą na płaszczyźnie $A B F E$ . Możemy skorzystac z własności planimetrii, więc wiemy, że ściana $A B F E$ sześcianu jest kwadratem i stąd boki $A B$ i $E F$ tego kwadratu są równoległe. Zatem boki te leżą na prostych równoległych zawierających te boki.

Na płaszczyźnie możliwe są tylko dwa położenia dwóch prostych: proste przecinające się (w jednym punkcie) albo proste równoległe, czyli takie, które nie mają punktów wspólnych lub pokrywają się.

Jeśli rozważamy dwie proste w przestrzeni, to mogą przeciąć się w jednym punkcie, pokrywać się lub nie mieć punktów wspólnych. W odróżnieniu od własności planimetrii proste, które nie mają punktów wspólnych nie muszą być równoległe.

Wykorzystujemy aksjomat równoległości do zdefiniowania prostych równoległych w przestrzeni. Mówimy, że dwie proste są równoległe, jeżeli leżą na jednej płaszczyźnie i są równoległe na tej płaszczyźnie. Przyjmujemy, że równe proste są równoległe. Podobnie jak w planimetrii, jeżeli proste $k$ , $l$ są równoległe, to piszemy $k ∥ l$ .

Na rysunku czerwona prosta jest prostą równoległą do prostej $D C$ i przechodzącą przez punkt $B$ , leży ona na płaszczyźnie wyznaczonej przez punkty $B$ , $C$ , $D$ . Niebieska prosta jest prostą równoległą do prostej $D C$ i przechodzącą przez punkt $A$ , leży ona na płaszczyźnie wyznaczonej przez punkty $A$ , $C$ , $D$ .

R13CK91EeKf57

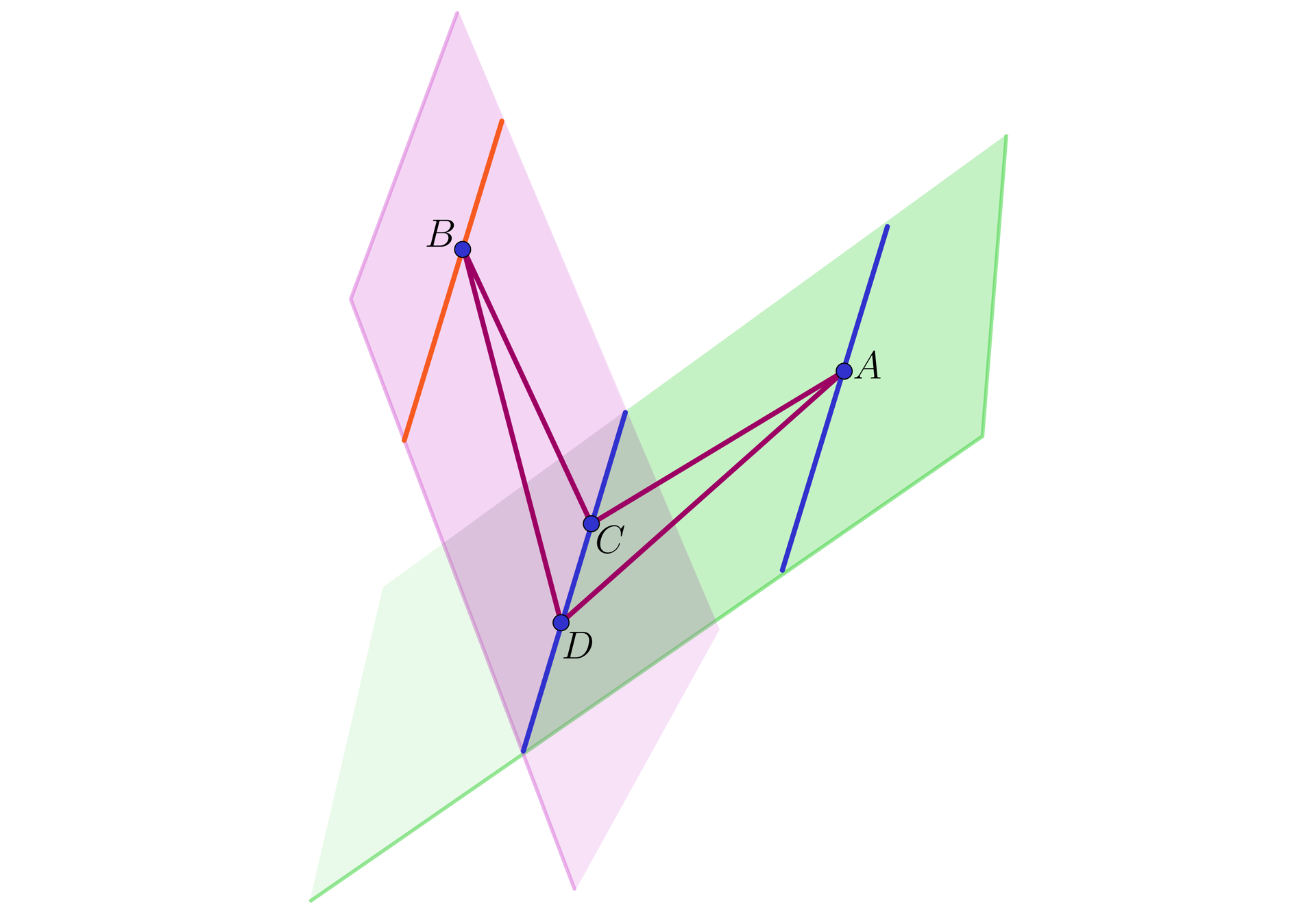
Ilustracja przedstawia dwie przecinające się pod kątem ostrym płaszczyzny. Na linii będącej linią przecięcia się płaszczyzn zaznaczono dwa punkty C oraz D. Na każdej z płaszczyzny zaznaczono linie równoległe do linii przecięcia się płaszczyzn, na jednej płaszczyźnie na linii równoległej zaznaczono punkt B, a na drugiej płaszczyźnie na linii równoległej zaznaczono punkt A. Na płaszczyznach zaznaczono następujące odcinki: na pierwszej BC oraz BD oraz na drugiej AC oraz AD.

Prosta równoległa do danej w przestrzeni

Własność: Prosta równoległa do danej w przestrzeni

Dla danej prostej $l$ i punktu B w przestrzeni istnieje dokładnie jedna prosta przechodząca przez B i równoległa do prostej $l$ .

Dowód

Jeżeli punkt $B$ należy do prostej $l$ , to prosta równoległa do $l$ i przechodząca przez punkt $B$ pokrywa się z prostą $l$ .

Załóżmy, że proste $k$ , $m$ są równoległe do prostej $l$ i przechodzą przez punkt $B$ nienależący do $l$ . Niech $π_{1}$ będzie płaszczyzną zawierającą $k$ i $l$ , a $π_{2}$ niech będzie płaszczyzną zawierającą $m$ i $l$ . Każda z tych płaszczyzn zawiera prostą $l$ i punkt $B$ , ale istnieje tylko jedna taka płaszczyzna, więc $π_{1} = π_{2}$ . Z aksjomatu równoległości wynika, że wtedy $k = m$ .

Z powyższej własności wnioskujemy, że jeśli dwie różne proste są równoległe do trzeciej prostej, to nie mają punktów wspólnych.

Przykład 2

Pokażemy, że krawędzie $A B$ i $G H$ sześcianu przedstawionego na rysunku zawarte są w prostych równoległych, a krawędzie $A B$ i $G F$ zawarte są w prostych, które nie mają punktów wspólnych, ale nie są równoległe.

RKFNBSj7xKtm6

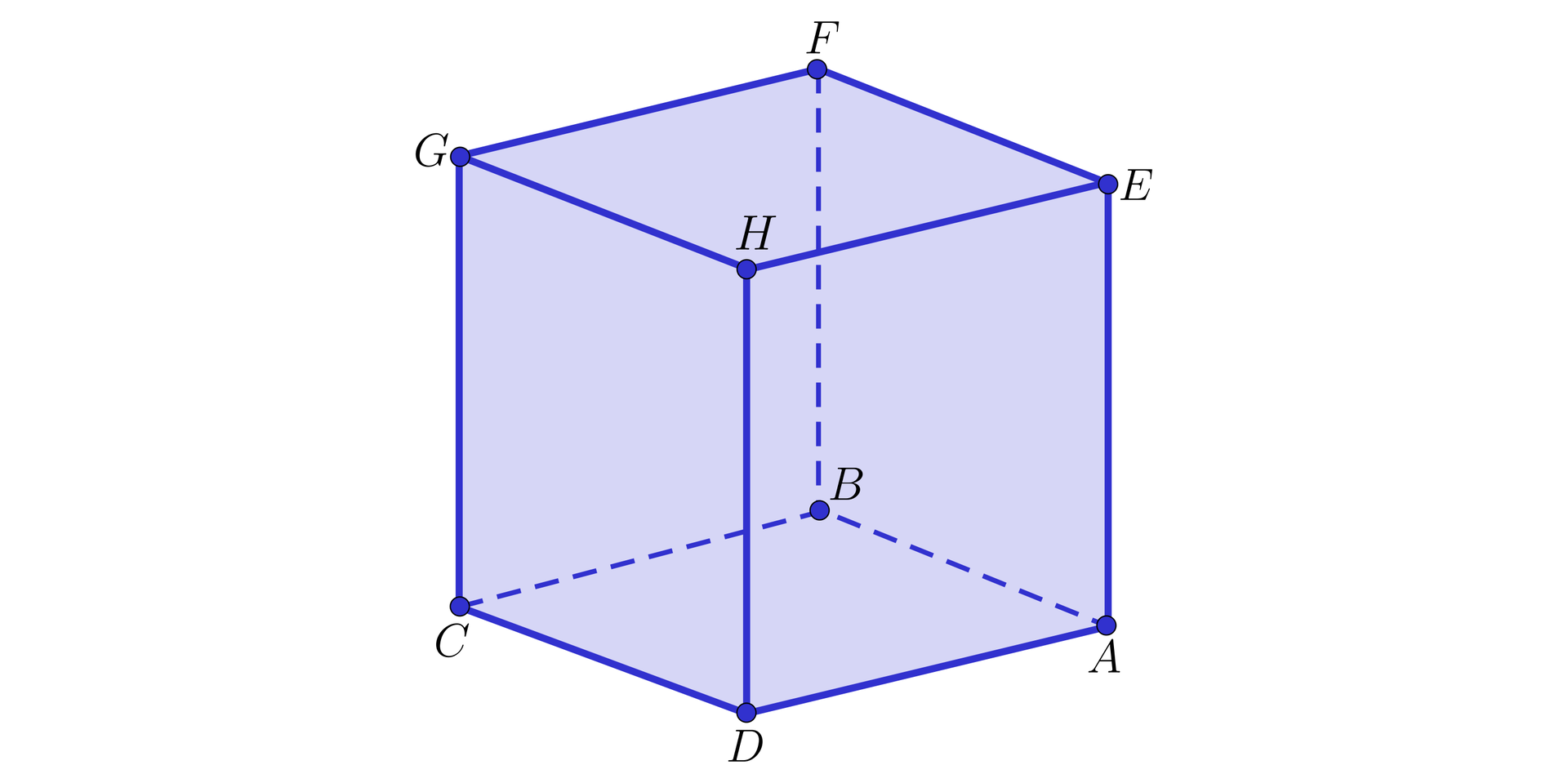
Rozwiązanie

Rzeczywiście, krawędzie $A B$ i $G H$ leżą na płaszczyźnie zawierającej przekrój $A B G H$ . Przekrój ten jest prostokątem, więc jego boki $A B$ i $G H$ są równoległe. Stąd proste zawierające te boki są równoległe.

Proste zawierające krawędzie $A B$ i $G F$ nie mają punktów wspólnych, bo leżą na płaszczyznach, które nie mają punktów wspólnych (wyznaczonych przez ściany $A B C D$ i $E F G H$ ). Nie istnieje natomiast płaszczyzna, która zawierałaby prostą $A B$ i prostą $G F$ jednocześnie.

Proste w przestrzeni, które nie mają punktów wspólnych i nie są równoległe nazywamy prostymi skośnymi.

Odległość punktu

P

od prostej

l

Definicja: Odległość punktu

P

od prostej

l

Jest to długość najkrótszego odcinka łączącego punkt $P$ z punktem na prostej. Ponieważ punkt $P$ i prosta $l$ leżą w jednej płaszczyźnie, to możemy skorzystać z własności planimetrii, która charakteryzuje odległość punktu $P$ od prostej $l$ jako długość odcinka $P P'$ , gdzie $P'$ jest punktem przecięcia prostej $l$ z prostą prostopadłą do $l$ poprowadzoną przez punkt $P$ .

Odległość między prostymi równoległymi w przestrzeni

Własność: Odległość między prostymi równoległymi w przestrzeni

Jeżeli proste są równoległe w przestrzeni, to odległość dowolnego punktu jednej prostej od drugiej prostej jest stała niezależnie od wyboru tego punktu.

Dowód

Jeżeli proste są równoległe, to leżą w jednej płaszczyźnie. Zatem wystarczy skorzystać z własności planimetrii, gdzie zachodzi omawiana własność.

Z powyższej własności wynika, że można mówić o odległości między prostymi równoległymi, która jest równa odległości dowolnego punktu na jednej prostej od drugiej prostej.

Płaszczyzna wyznaczona przez dwie różne proste równoległe

Własność: Płaszczyzna wyznaczona przez dwie różne proste równoległe

Istnieje dokładnie jedna płaszczyzna zawierająca dwie różne proste równoległe.

Dowód

Jeżeli proste $l$ , $l'$ są różne i równoległe, to dwa dowolne różne punkty $A$ , $B$ na prostej $l$ i punkt $C$ na prostej $l'$ nie leżą na jednej prostej, więc wyznaczają dokładnie jedną płaszczyznę. Ponieważ proste $l$ , $l'$ leżą na wspólnej płaszczyźnie zawierającej punkty $A$ , $B$ , $C$ , to jest tylko jedna płaszczyzna zawierająca te proste.

Z powyższej własności wynika, że jeśli dwie krawędzie figury przestrzennej są równoległe, to leżą na jednej płaszczyźnie. Stąd można wykonać przekrój płaszczyznowy tej figury poprowadzony przez krawędzie równoległe. W przypadku, gdy te krawędzie są sąsiednie, to można wyznaczyć płaszczyznę zawierająca ścianę tej figury.

Przykład 3

Na prostej $l$ zaznaczono punkty $A$ , $B$ tak, że $|A B| = 4$ . Punkt $C$ jest położony w przestrzeni tak, że $|A C| = |B C| = 4$ . Wyznaczymy odległość prostej $l$ od prostej $l'$ równoległej do $l$ poprowadzonej przez punkt $C$ .

Rozwiązanie

Zauważmy, że punkt $C$ nie leży na prostej $l$ , bo w przeciwnym przypadku, jeśli $|A C| = 4$ , to $|B C| = 0$ lub $|B C| = 8$ , co jest sprzeczne z założeniem.

Proste $l$ , $l'$ są równoległe, więc leżą na jednej płaszczyźnie. Stąd punkty $A$ , $B$ , $C$ też leżą na tej płaszczyźnie, więc tworzą trójkąt równoboczny o boku długości $4$ . Odległość punktu $C$ od prostej $l$ jest równa długości wysokości w trójkącie $A B C$ . Korzystając ze wzoru na wysokość w trójkącie równobocznym dostajemy, że odległość między prostymi wynosi $\frac{4 \sqrt{3}}{2} = 2 \sqrt{3}$ .

Prosta równoległa do danej prostej i płaszczyzna przechodząca przez daną prostą

Własność: Prosta równoległa do danej prostej i płaszczyzna przechodząca przez daną prostą

Jeżeli prosta $l$ leży na płaszczyźnie $π$ i punkt $A$ nie należy do $π$ , to prosta $l'$ równoległa do $l$ i przechodząca przez punkt $A$ nie ma punktów wspólnych z płaszczyzną $π$ .

Dowód

Wybieramy punkt $A$ , który nie należy do płaszczyzny $π$ . Na mocy aksjomatu równoległości istnieje prosta $l'$ przechodząca przez punkt $A$ i równoległa do $l$ . Gdyby punkt $B$ był punktem wspólnym prostej $l'$ i płaszczyzny $π$ , to należałby też do płaszczyzny $π_{1}$ wyznaczonej przez proste $l$ , $l'$ . Wtedy płaszczyzny $π$ , $π_{1}$ zawierają prostą $l$ i punkt $B$ , a taka płaszczyzna może być tylko jedna. Stąd $π = π_{1}$ co jest sprzeczne z założeniem, że $A$ nie należy do $π$ .

Z powyższej własności wynika, że jeśli różne proste $l$ , $l'$ są równoległe, to dowolna płaszczyzna zawierająca $l$ i różna od wspólnej płaszczyzny prostych $l$ , $l'$ nie ma punktów wspólnych z $l'$ .

Krawędź przecięcia płaszczyzny i płaszczyzny przechodzącej przez prostą

Własność: Krawędź przecięcia płaszczyzny i płaszczyzny przechodzącej przez prostą

Jeżeli prosta $l$ nie ma punktów wspólnych z płaszczyzną $π$ , to płaszczyzna wyznaczona przez prostą $l$ i dowolny punkt $A$ należący do płaszczyzny $π$ przecina płaszczyznę $π$ wzdłuż prostej równoległej do prostej $l$ i zawierającej punkt $A$ .

Dowód

Wybieramy dowolny punkt $A$ na płaszczyźnie $π$ i prowadzimy płaszczyznę przez prostą $l$ . Wtedy krawędź przecięcia tych płaszczyzn (prosta $l'$ ) oczywiście zawiera punkt $A$ i leży w tej samej płaszczyźnie co prosta $l$ . Ponadto, proste te nie mają punktów wspólnych, bo prosta $l'$ leży na płaszczyźnie, o której zakładamy, że nie ma punktów wspólnych z $l$ .

Proste równoległe do trzeciej prostej

Twierdzenie: Proste równoległe do trzeciej prostej

Jeżeli prosta $k$ jest równoległa do prostej $l$ , a prosta $l$ jest równoległa do prostej $m$ , to prosta $k$ jest równoległa do prostej $m$ .

Dowód

Zakładamy, że $k ∥ l$ i $l ∥ m$ . Chcemy pokazać, że $k ∥ m$ . Jeżeli $k$ , $l$ , $m$ leżą na jednej płaszczyźnie, to z własności planimetrii $k ∥ m$ . Załóżmy, że $k$ , $l$ , $m$ nie leżą na jednej płaszczyźnie. Niech $π_{1}$ będzie płaszczyzną poprowadzoną przez prostą $m$ i punkt $A$ leżący na prostej $k$ , a $π_{2}$ - płaszczyzną zawierającą prostą $l$ i punkt $A$ . Płaszczyzny te przecinają się wzdłuż prostej $n$ . Wtedy punkt $A$ należy do prostej $n$ .

R7M0sTKCGJUCn

Ilustracja przedstawia dwie przecinające się pod kątem ostrym płaszczyzny, są one podpisane π1 oraz π2. Na linii k, która jest linią przecięcia się płaszczyzn zaznaczono punk A. Linia k należy do prostej n. Na płaszczyźnie π1 znajduje się linia m. Na płaszczyźnie π2 znajduje się linia l.

Ponieważ prosta $l$ nie ma punktów wspólnych z płaszczyzną $π_{1}$ , to prosta $n$ jest równoległa do $l$ i zawiera punkt $A$ .

Z aksjomatu równoległości wynika, że może być tylko jedna taka prosta, więc $k = n$ .

Z drugiej strony, prosta $m$ nie ma punktów wspólnych z płaszczyzną $π_{2}$ , więc prosta $n$ jest równoległa do $m$ .

Stąd $k ∥ m$ .

Przykład 4

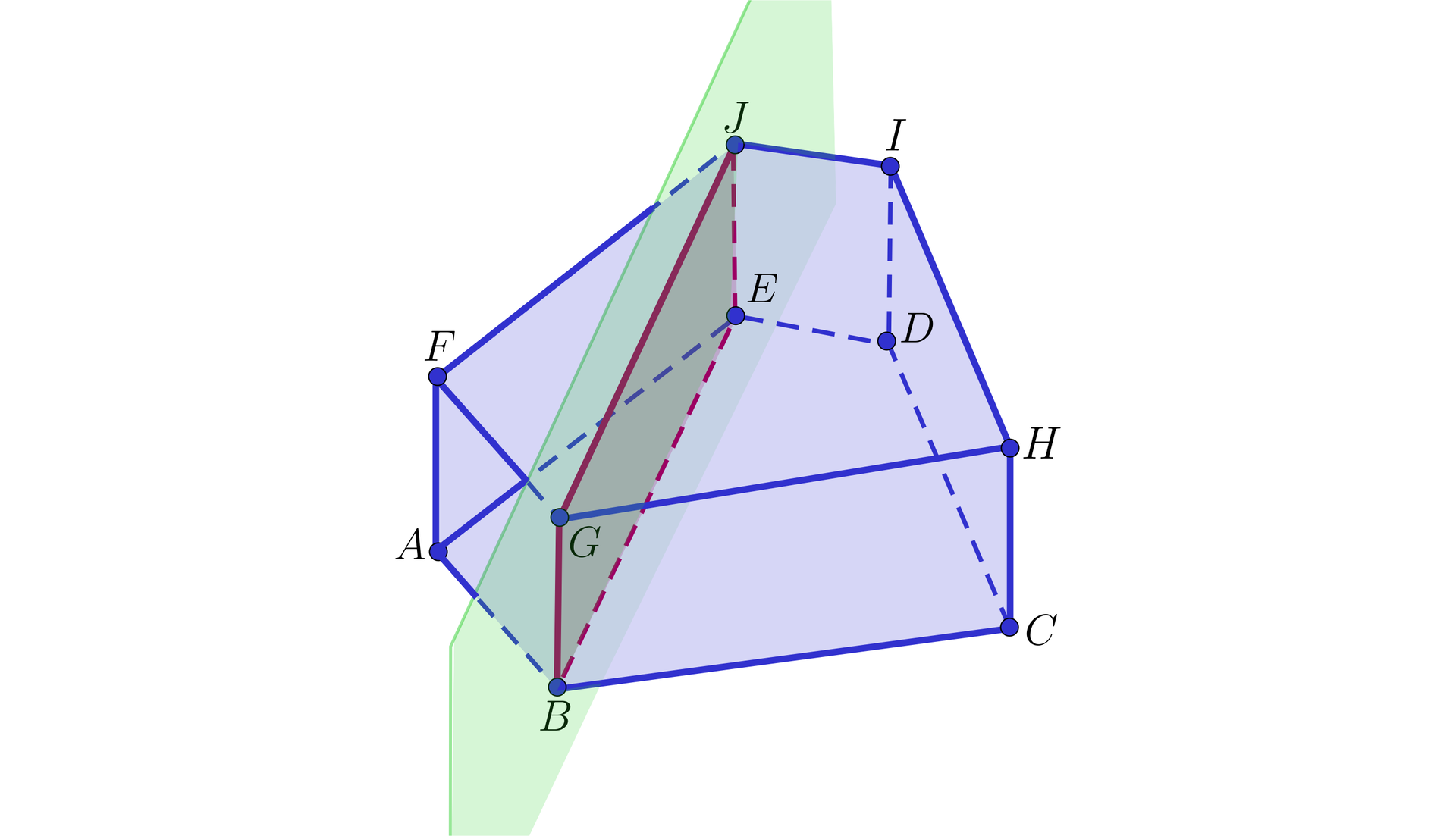
Pokażemy, że w graniastosłupie o podstawie pięciokąta wszystkie krawędzie boczne są parami równoległe.

Rf6JzvjKujjdF

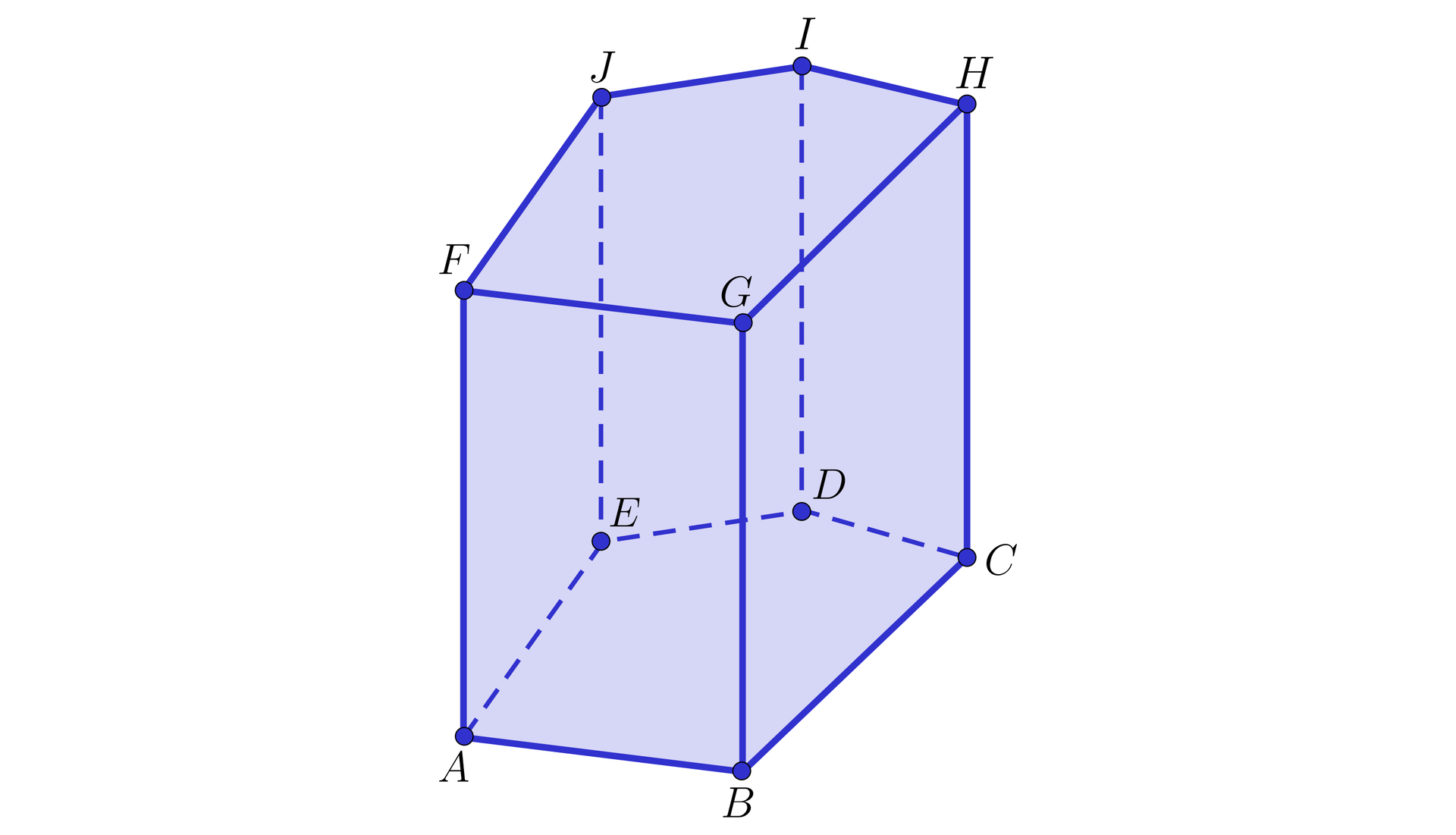
Ilustracja przedstawia pięciokąt o wierzchołkach A B C D E F G H I J.

Rozwiązanie

Z własności graniastosłupów wynika, że ściany boczne są równoległobokami, więc sąsiednie krawędzie są równoległe. Aby pokazać, że przeciwległe krawędzie, na przykład $A F$ i $C H$ są równoległe, korzystamy z powyższego twierdzenia, bo $A F ∥ B G$ , $B G ∥ C H$ i stąd $A F ∥ C H$ .

Przykład 5

Pokażemy, że w graniastosłupie o podstawie pięciokąta można wykonać przekrój płaszczyznowy dla każdej pary przeciwległych krawędzi bocznych.

Rozwiązanie

Ponieważ wszystkie krawędzie boczne są równoległe, to przez każdą parę przeciwległych krawędzi można poprowadzić płaszczyznę, czyli wykonać przekrój.

R12XN234du1Am

Ilustracja przedstawia pięciokąt, w którym wierzchołki A B C D E nalezą do dolnej podstawy a wierzchołki F G H I J należą do górnej podstawy. Przez wierzchołki B E G J przeprowadzono płaszczyznę. Wierzchołki B E J G tworzą prostokąt.

Prosta równoległa do prostej przebijającej płaszczyznę

Własność: Prosta równoległa do prostej przebijającej płaszczyznę

Niech $l$ będzie dowolną prostą, która przebija płaszczyznę $π$ w punkcie $A$ oraz niech $k$ będzie prostą równoległą do $l$ przechodzącą przez punkt $B$ . Wtedy prosta $k$ przebija płaszczyznę $π$ w punkcie leżącym na wspólnej krawędzi płaszczyzny $π$ i płaszczyzny wyznaczonej przez proste $k$ , $l$ .

Dowód

Niech $B$ będzie dowolnym punktem przestrzeni. Prowadzimy prostą $k$ równoległą do $l$ przechodzącą przez punkt $B$ . Proste $k$ , $l$ są równoległe, więc leżą na jednej płaszczyźnie $π_{1}$ . Wtedy płaszczyzny $π$ , $π_{1}$ mają punkt wspólny $A$ , więc mają wspólną prostą $m$ . Załóżmy, że prosta $k$ nie ma punktu wspólnego z prostą $m$ . Wtedy $k$ , $m$ są równoległe, bo leżą w jednej płaszczyźnie i nie mają punktów wspólnych. Stąd $l$ jest też równoległa do $m$ , a ponieważ $m$ i $l$ mają punkt wspólny, to $l = m$ i stąd $l$ leży na płaszczyźnie $π$ . To jest sprzeczne z założeniem, że $m$ przebija $π$ . Zatem prosta $k$ przebija płaszczyznę $π$ w punkcie leżącym na wspólnej krawędzi płaszczyzn $π$ , $π_{1}$ .

Jeżeli prosta $l$ przebija płaszczyznę $π$ i dany jest punkt $B$ w przestrzeni. Wtedy punkt $B'$ przebicia płaszczyzny $π$ prostą $k$ równoległą do $l$ i przechodzącą przez punkt $B$ nazywamy rzutem równoległym punktu $B$ na płaszczyznę $π$ w kierunku prostej $l$ .

Rzutem równoległym figury $F$ na płaszczyznę $π$ w kierunku prostej $l$ nazywamy figurę $F'$ złożoną z rzutów na tę płaszczyznę wszystkich punktów figury $F$ .

Najczęściej stosuje się rzut prostopadły (lub po prostu rzut) na płaszczyznę $π$ , który jest rzutem równoległym w kierunku prostej $l$ prostopadłej do płaszczyzny $π$ .

Pęk prostych równoległych

Zbiór prostych równoległych do danej prostej $l$ nazywamy pękiem prostych równoległych do $l$ .

Rozważmy pęk wszystkich prostych równoległych do $l$ . Ponieważ przez dowolny punkt w przestrzeni można poprowadzić prostą równoległą do $l$ , to każdy punkt przestrzeni należy do pęku wszystkich prostych równoległych do $l$ . Zatem przestrzeń jest pękiem wszystkich prostych równoległych do $l$ .

Rozważmy płaszczyznę $π$ i prostą $l$ leżącą na tej płaszczyźnie. Wtedy dla dowolnego punktu $A$ na tej płaszczyźnie można poprowadzić prostą równoległą do $l$ . Stąd wynika, że każdy punkt płaszczyzny leży na pewnej prostej równoległej do $l$ . Zatem płaszczyzna $π$ jest pękiem prostych równoległych do $l$ i leżących na płaszczyźnie $π$ .

Przykład 6

Pokażemy, że jeżeli nierównoległe proste $l$ , $k$ leżą na płaszczyźnie $π$ , to płaszczyzna $π$ jest pękiem prostych równoległych do $l$ i przecinających prostą $k$ .

Rozwiązanie

Na rysunku zaznaczono proste $l$ , $k$ i poprowadzono kilka prostych równoległych do $l$ przez wybrane punkty na prostej $k$ .

Rg9wV1Rk4DLDs

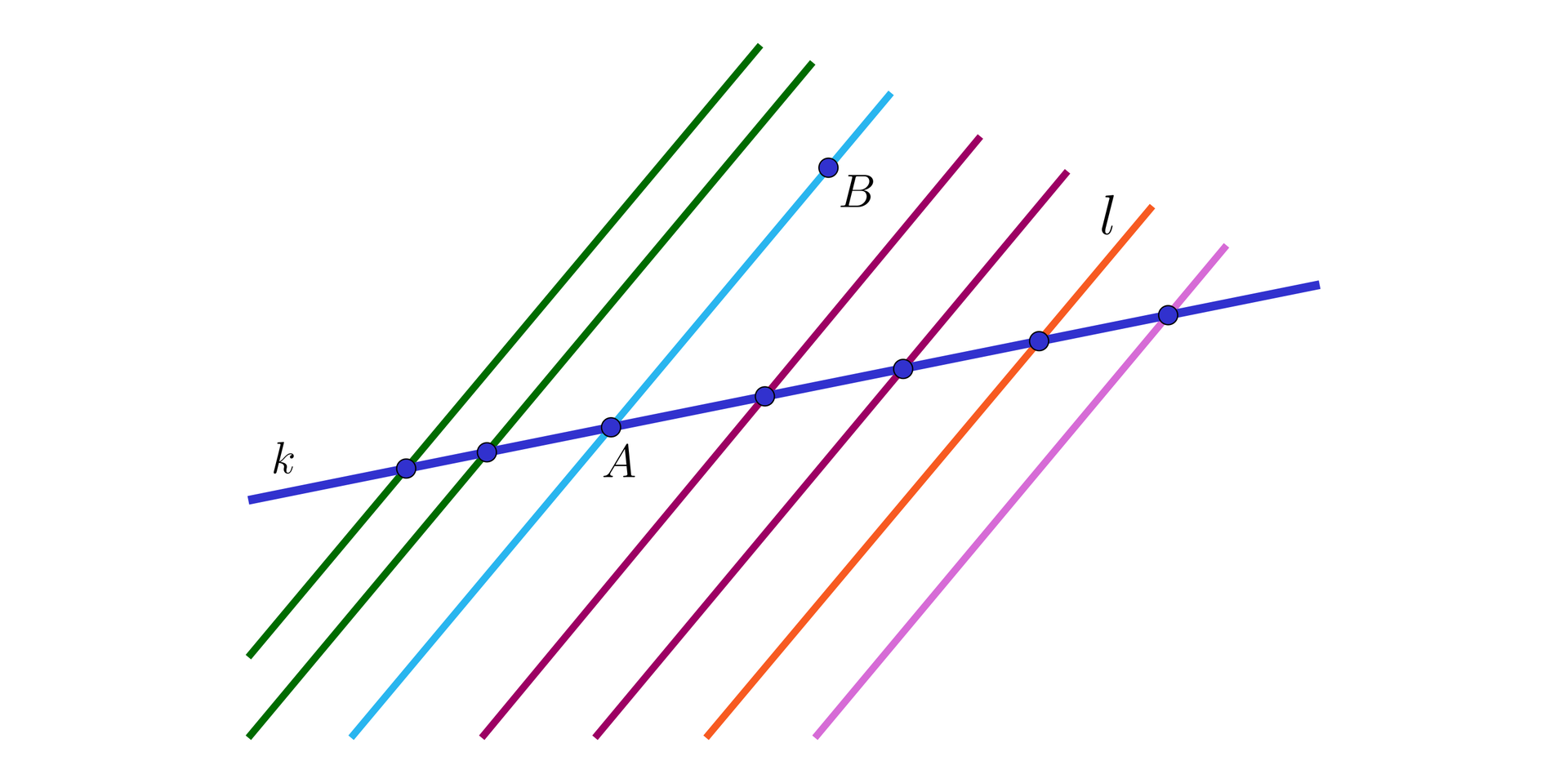
Ilustracja przedstawia siedem równoległych do siebie ukośnych prostych, przez wszystkie te proste poprowadzono prostą k. W miejscy przecięcia się trzeciej prostej z prostą k zaznaczono punkt A. Na tej samej prostej nad prostą k zaznaczono punkt B. Szóstą prostą podpisano literą l.

Na mocy aksjomatu równoległości taką konstrukcję można wykonać dla dowolnego punktu $A$ na prostej $k$ . Niech $B$ będzie dowolnym punktem płaszczyzny $π$ . Wtedy można przez punkt $B$ poprowadzić prostą $l'$ równoległą do $l$ . Ponieważ proste $l$ , $k$ nie są równoległe, to proste $l'$ , $k$ też nie są równoległe. Stąd prosta $l'$ przecina prostą $k$ w pewnym punkcie $B'$ , więc pokrywa się z prostą równoległą do $l$ poprowadzoną przez punkt $B'$ . Zatem płaszczyzna $π$ jest pękiem prostych równoległych do $l$ i przecinających prostą $k$ .

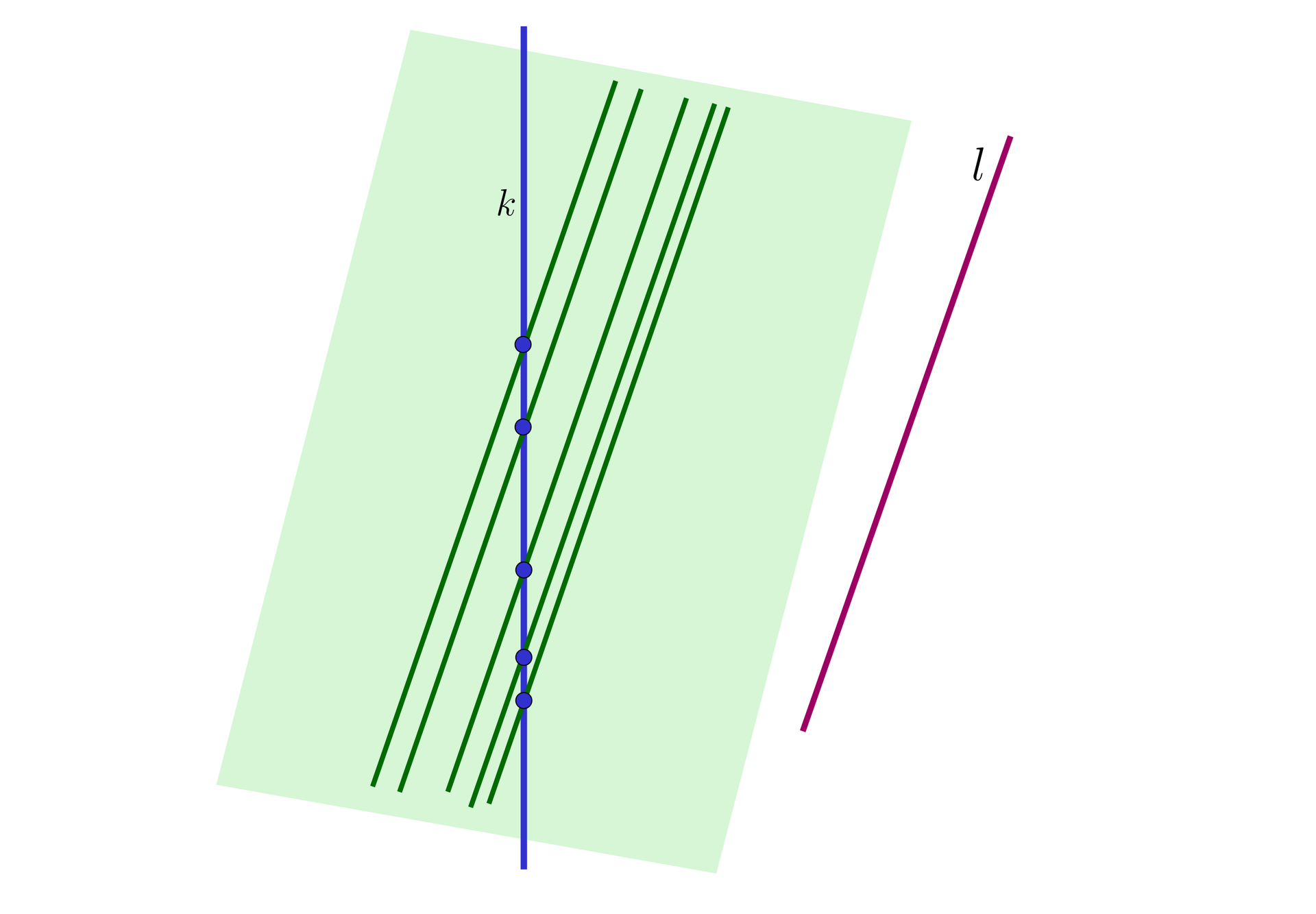
Rozważmy teraz dwie nierównoległe proste $l$ , $k$ w przestrzeni. Przez każdy punkt prostej $k$ prowadzimy prostą równoległą do $l$ . Wtedy uzyskany w ten sposób pęk prostych równoległych do $l$ tworzy płaszczyznę zawierającą prostą $k$ .

Na rysunku przedstawiono proste $l$ , $k$ i poprowadzono kilka prostych równoległych do $l$ przez wybrane punkty na prostej $k$ . Płaszczyzna powstała jako pęk prostych równoległych do $l$ i przecinających prostą $k$ zaznaczona jest na zielono.

RXmSPXYrTlav9

Ilustracja przedstawia płaszczyznę na której leży pięć równoległych do siebie prostych, przez wszystkie te proste poprowadzono prostą k, która ma z nimi jeden punkt wspólny. Obok płaszczyzny narysowano prostą l.

Kolejnym ważnym zastosowaniem pęku prostych równoległych jest tworzenie figur (brył) przestrzennych.

Na płaszczyźnie mamy pewną figurę płaską, na przykład trójkąt. Ustalamy prostą $l$ , która ma jeden punkt wspólny z płaszczyzną. W kolejnym kroku prowadzimy przez każdy punkt trójkąta prostą równoległą do $l$ . Uzyskany w ten sposób pęk prostych równoległych do $l$ tworzy nieskończoną belkę o przekroju trójkątnym.

Na rysunku zaznaczono kilka punktów trójkąta i poprowadzono proste równoległe do prostej $l$ .

Rtn4ixoBpay9p

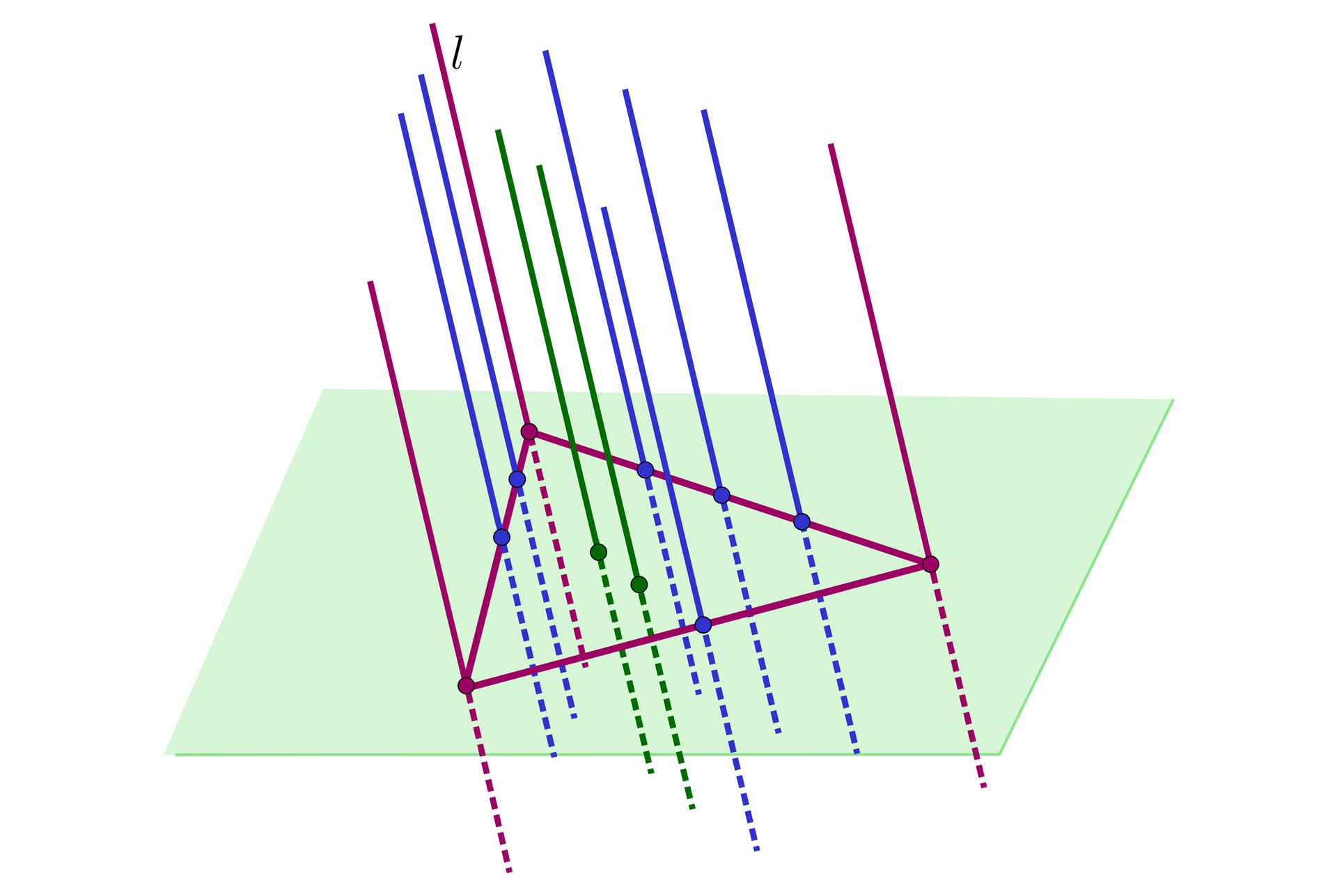
Ilustracja przedstawia płaszczyznę przez którą przechodzi jedenaście równoległych do siebie prostych. Trzy proste zaznaczone kolorem fioletowym są wierzchołkami trójkąta, który został zaznaczony na płaszczyźnie, jedna z fioletowych prostych jest podpisana literą l. Sześć prostych zaznaczonych kolorem niebieskim przecinają płaszczyznę na bokach zaznaczonego trójkąta, a dwie zielone proste przecinają płaszczyznę wewnątrz trójkąta.

Czerwone punkty są wierzchołkami tego trójkąta. Pęk prostych równoległych do $l$ poprowadzonych przez wierzchołki (czerwone proste) utworzy krawędzie powstałej bryły.

Punkty niebieskie i czerwone leżą na bokach trójkąta, więc pęk prostych równoległych do $l$ poprowadzonych przez wszystkie punkty na bokach trójkąta utworzy ściany powstałej bryły, czyli powierzchnię tej bryły.

Zielone punkty leżą we wnętrzu trójkąta. Wszystkie punkty trójkąta wyznaczają pęk prostych równoległych do $l$ , który stanowi całą bryłę.

Bryła, która powstaje w ten sposób jest nieskończonym pochylonym graniastosłupem (krawędzie boczne nie muszą być prostopadłe do podstawy).

Na rysunku zaznaczono kilka punktów koła i poprowadzono proste równoległe do prostej $l$ .

R1cwhU2JTFiZO

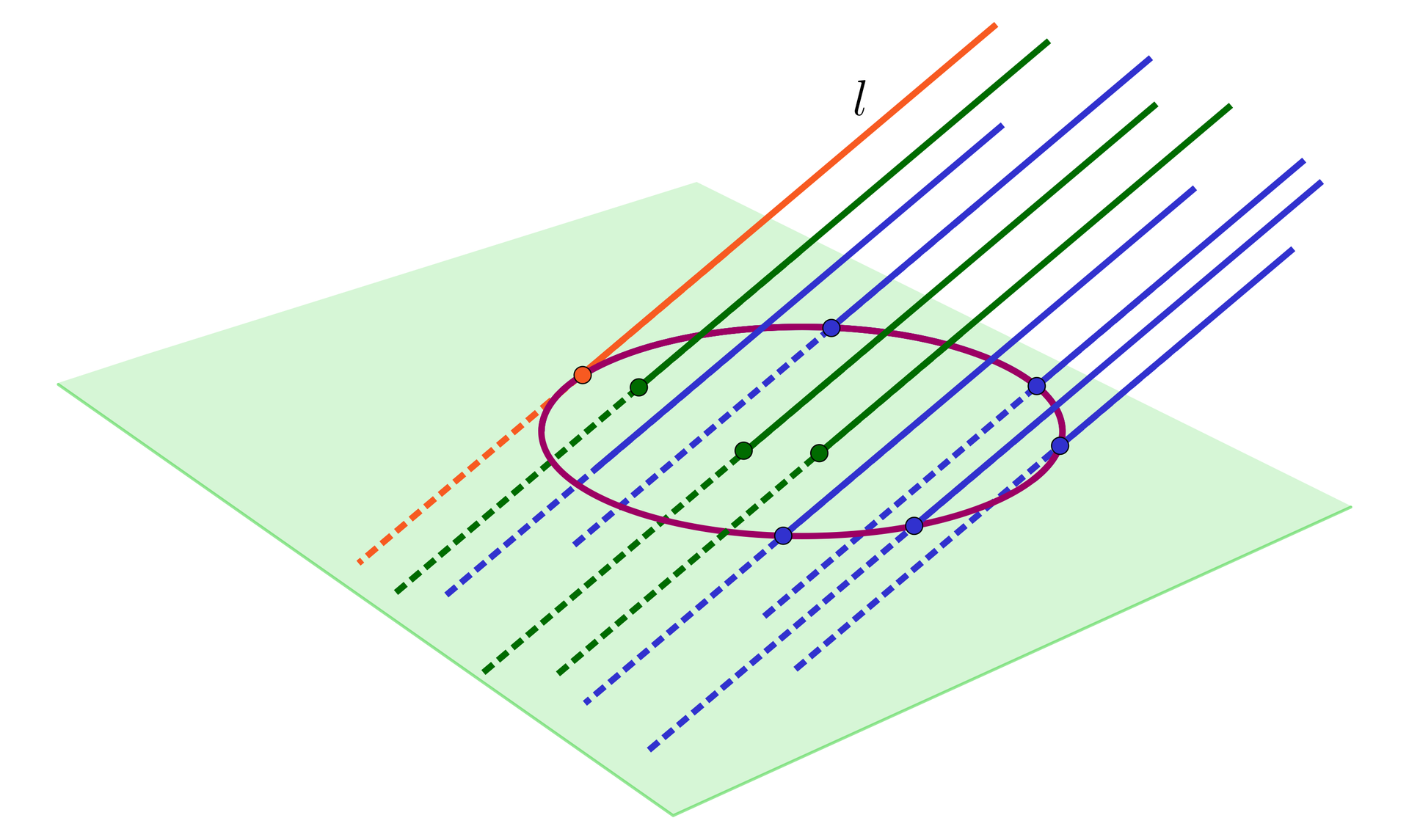
Ilustracja przedstawia płaszczyznę przez którą przechodzi dziesięć równoległych do siebie prostych. Jedna prosta zaznaczona kolorem pomarańczowym przechodzi przez okrąg który został zaznaczony na płaszczyźnie i jest podpisana literą l. Sześć prostych zaznaczonych kolorem niebieskim również przecinają płaszczyznę na okręgu , a trzy zielone proste przecinają płaszczyznę wewnątrz okręgu.

Pęk prostych równoległych do $l$ poprowadzonych przez wszystkie punkty koła utworzy nieskończoną owalną belkę (nieskończony pochylony walec). Punkty na okręgu wyznaczają pęk prostych równoległych do $l$ tworzący powierzchnię tej belki.

Można uzyskać również bryły i powierzchnie ograniczone biorąc fragment między dwiema płaszczyznami jak na rysunku. Figura na płaszczyźnie zielonej jest przekrojem nieskończonego walca tą płaszczyzną.

R1bdKeBrH6P8A

Ilustracja przedstawia dwie przecinające się pod kątem płaszczyzny. Obie płaszczyzny przecina dziesięć prostych w następujący sposób: Jedna prosta zaznaczona kolorem pomarańczowym przechodzi przez okręgi które zostały zaznaczone na obu płaszczyznach i jest podpisana literą l. Sześć prostych zaznaczonych kolorem niebieskim również przecinają obie płaszczyzny na okręgu , a trzy zielone proste przecinają płaszczyzny wewnątrz okręgów.

Z drugiej strony, każdy punkt tego przekroju powstał w wyniku rzutowania równoległego punktów danego koła na płaszczyznę zieloną w kierunku prostej $l$ .

W ten sposób dostajemy znane bryły, między innymi takie jak, walce i graniastosłupy.

Pęk prostych równoległych wyznaczonych przez dwie proste równoległe

Własność: Pęk prostych równoległych wyznaczonych przez dwie proste równoległe

Załóżmy, że dwie proste równoległe $k$ , $m$ leżą na płaszczyźnie $π_{1}$ . Prosta $l$ ma jeden punkt wspólny z płaszczyzną $π_{1}$ oraz ma jeden punkt wspólny z drugą płaszczyzną $π_{2}$ . Wtedy w przekroju pęku prostych równoległych do prostej $l$ wyznaczonego przez proste $k$ , $m$ płaszczyzną otrzymujemy proste równoległe.

Dowód

Zwróćmy uwagę na rysunek.

R18mY8uUEGznS

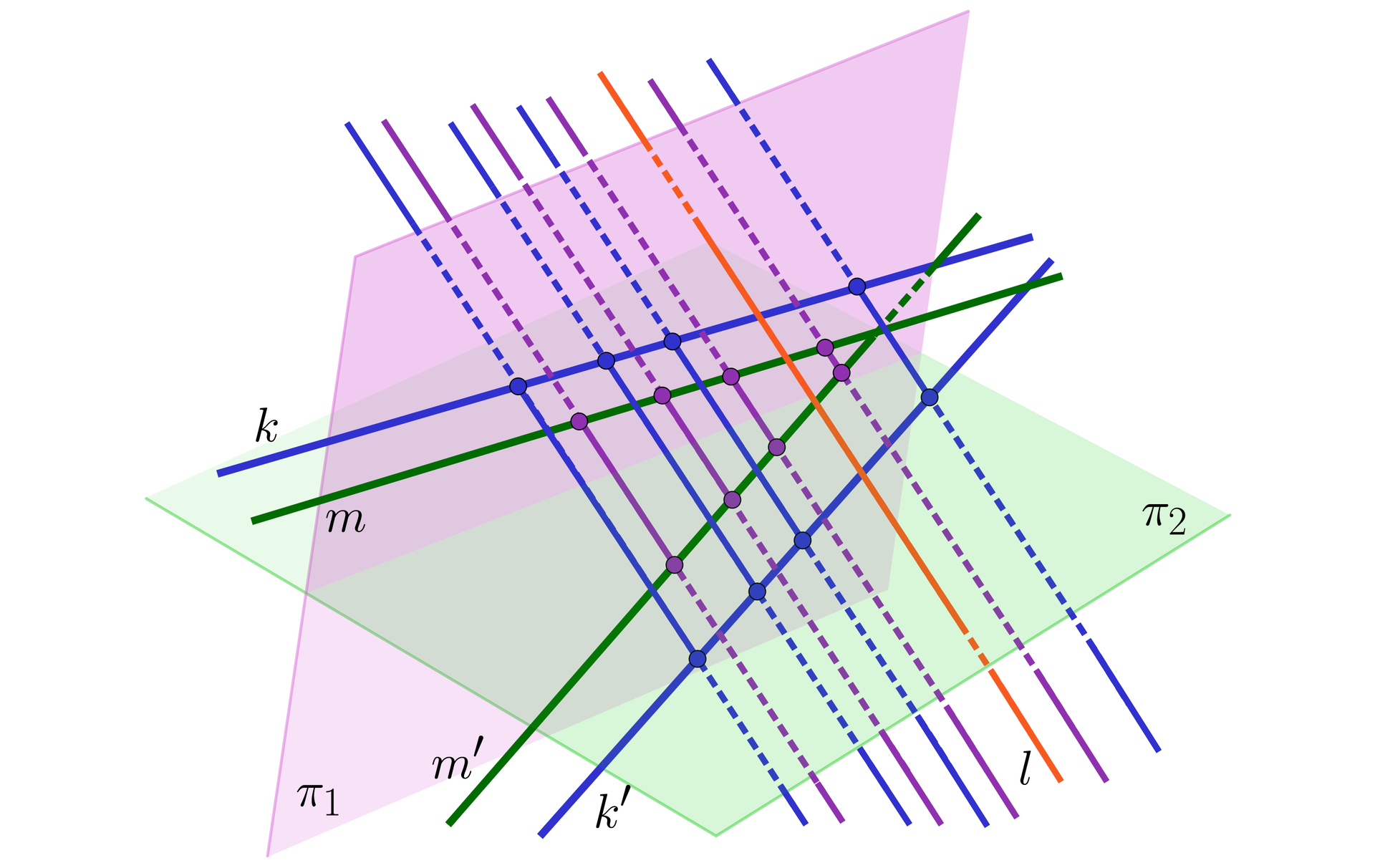
Ilustracja przedstawia dwie przecinające się pod kątem ostrym płaszczyzny, są one podpisane π1 oraz π2. Na płaszczyźnie π1 znajdują się dwie równoległe do siebie proste m oraz k. Przez obie płaszczyzny przechodzi prosta l, która ma z każdą z nich jeden punkt wspólny, oprócz prostej l przez płaszczyzny przechodzi osiem prostych równoległych do prostej l, na zmianę są to niebieskie i fioletowe proste. Na płaszczyźnie π2 znajdują się dwie proste m' oraz k'. Wszystkie niebieskie proste mają zaznaczone punkty wspólne na prostej k i prostej k', wszystkie zielone proste mają zaznaczone punkty wspólne z prostą m i prostą m'.

Rozważamy płaszczyznę, która jest pękiem prostych równoległych do prostej $l$ wyznaczonym przez prostą $k$ . Częścią wspólną tej płaszczyzny z $π_{2}$ jest prosta $k'$ . Podobnie, dla prostej $m$ otrzymujemy prostą $m'$ .

Załóżmy, że $P$ jest punktem wspólnym prostych $k'$ , $m'$ . Wtedy istnieje punkt $P'$ na prostej $k$ taki, że prosta $P P'$ należy do pęku prostych równoległych do prostej $l$ wyznaczonego przez prostą $k$ .

Podobnie, istnieje punkt $P''$ na prostej $m$ taki, że prosta $P''$ należy do pęku prostych równoległych do prostej $l$ wyznaczonego przez prostą $m$ . Stąd proste $P P'$ i $P P''$ są równoległe do $l$ i przechodzą przez punkt $P$ , więc $P P' = P P''$ . A ponieważ $P'$ i $P''$ są punktami przebicia prostej $P P'$ z płaszczyzną $π_{1}$ , to $P' = P''$ .

Stąd $k = m$ , bo są równoległe i mają punkt wspólny. Zatem $k' = m'$ .

Innymi słowy rzut równoległy prostych równoległych daje proste równoległe.

Słownik

przekrój bryły płaszczyzną (przekrój płaszczyznowy)

część wspólna bryły i płaszczyzny

Wprowadzenie

Animacja 3D

Aksjomat równoległości (postulat Euklidesa)

Pęk prostych równoległych

Słownik