Przeczytaj

W materiale omówimy wykres oraz własności funkcji kwadratowejfunkcji kwadratowej, gdy jest ona określona za pomocą wzoru w postaci kanonicznej $f (x) = a {(x - p)}^{2} + q$ , gdzie $a, p, q \in ℝ$ oraz $a \neq 0$ .

Naszkicujmy wykres funkcji kwadratowej określonej wzorem $f (x) = {(x - 3)}^{2} - 2$ .

Ze wzoru funkcji możemy odczytać, że:

$a = 1$ , zatem ramiona paraboliparabolaparaboli , która jest wykresem funkcji, są skierowane do góry,
wierzchołkiem paraboli, która jest wykresem tej funkcji, jest punkt o współrzędnych $(3, - 2)$ ,
osią symetrii paraboli jest prosta o równaniu $x = 3$ ,
zbiorem wartości funkcji jest przedział $⟨- 2, \infty)$ ,
funkcja jest malejąca w przedziale $(- \infty, 3⟩$ i rosnąca w przedziale $⟨3, \infty)$ ,
punkt przecięcia wykresu tej funkcji z osią $Y$ ma współrzędne $(0, 7)$ .

Wykres tej funkcji przedstawia się zatem następująco:

RMtOjUUSL5DG9

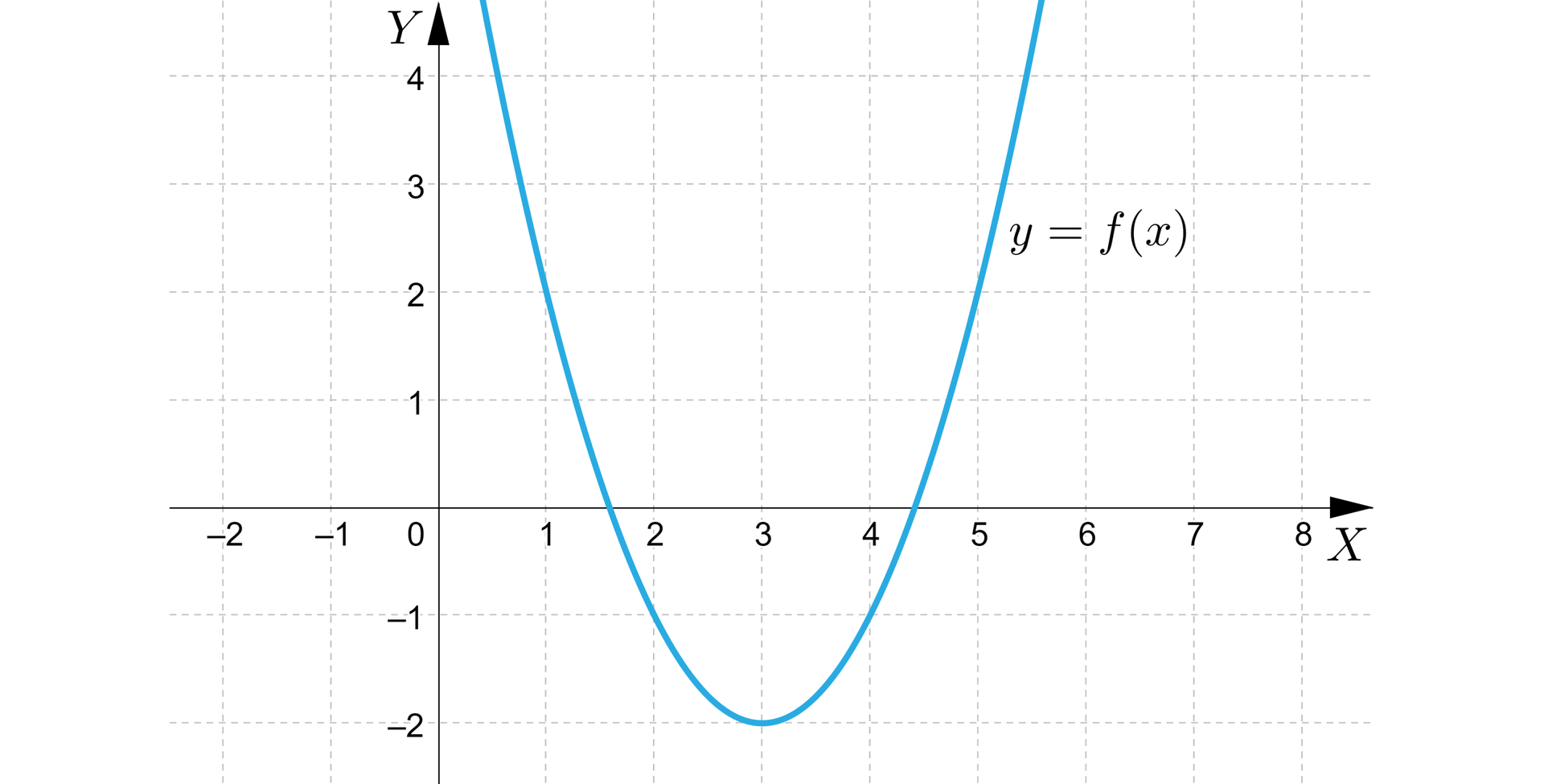
Ilustracja przedstawia poziomą oś X od minus dwóch do ośmiu i pionową oś Y od minus jedynki do pięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będącej parabola z ramionami skierowanymi w górę i wierzchołkiem w punkcie nawias trzy średnik minus dwa. Wykres funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias minus dwa średnik minus jeden koniec nawiasu oraz nawias cztery średnik minus jeden koniec nawiasu.

Ważne!

Wykres przedstawiony na rysunku możemy otrzymać poprzez przesunięcie wykresu funkcji określonej wzorem $g (x) = x^{2}$ o $3$ jednostki w prawo wzdłuż osi $X$ oraz $2$ jednostki w dół wzdłuż osi $Y$ .

Naszkicujmy wykres funkcji określonej wzorem $f (x) = - 2 {(x + 3)}^{2} + 4$ .

Ze wzoru funkcji możemy odczytać, że:

$a = - 2$ , zatem ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu,
wierzchołkiem paraboli, która jest wykresem tej funkcji, jest punkt o współrzędnych $(- 3, 4)$ ,
osią symetrii paraboli jest prosta o równaniu $x = - 3$ ,
zbiorem wartości funkcji jest przedział $(- \infty, 4⟩$ ,
funkcja jest rosnąca w przedziale $(- \infty, - 3⟩$ i malejąca w przedziale $⟨- 3, \infty)$ ,
punkt przecięcia wykresu tej funkcji z osią $Y$ ma współrzędne $(0, - 14)$ .

Wykres tej funkcji przedstawia się zatem następująco:

RBcpf94SulwcB

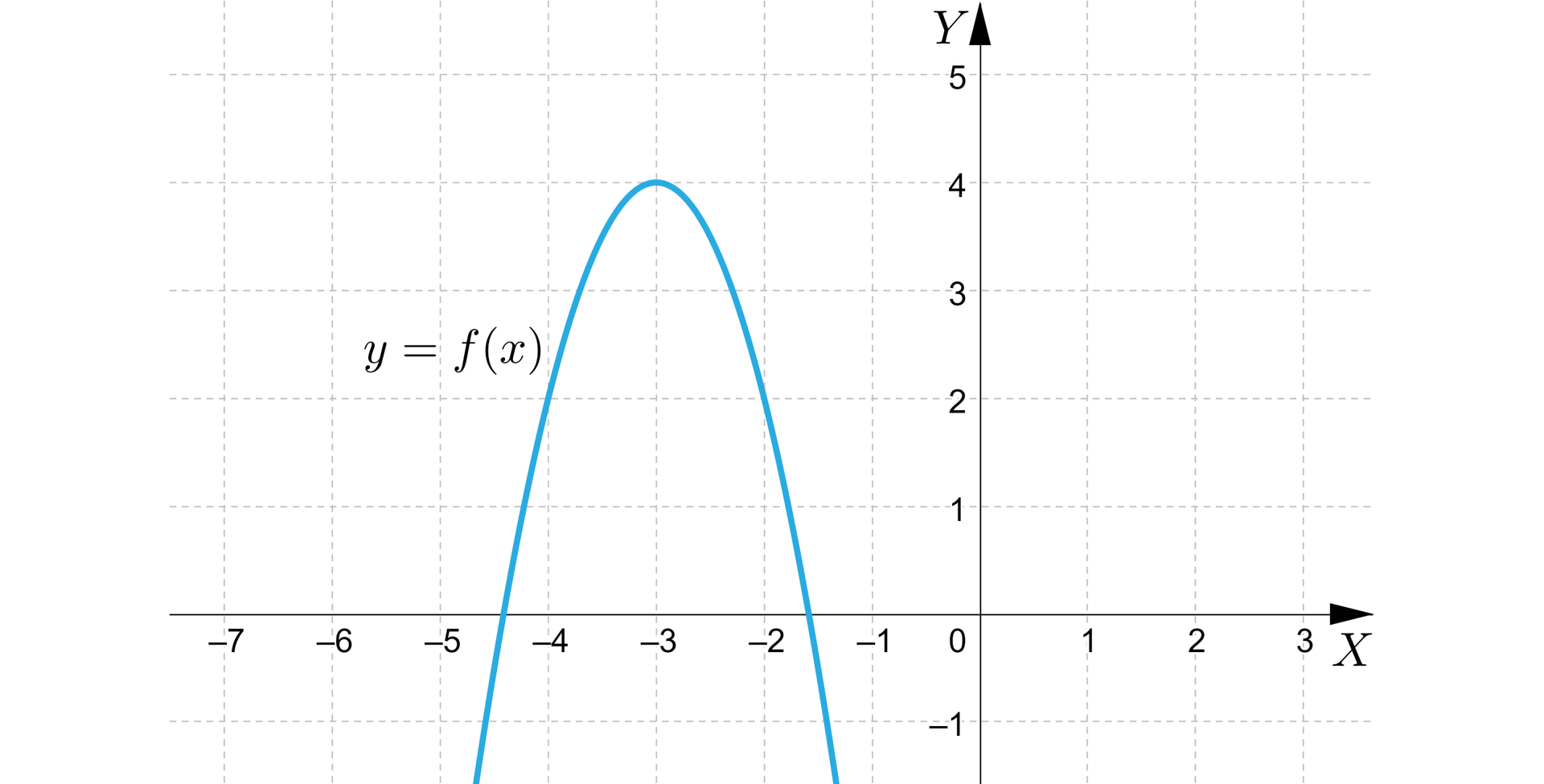
Ilustracja przedstawia poziomą oś X od minus siedmiu do trzech i pionową oś Y od minus jedynki do pięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będącej parabola z ramionami skierowanymi w dół i wierzchołkiem w punkcie nawias minus trzy średnik cztery. Wykres funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias minus cztery średnik dwa koniec nawiasu oraz nawias minus dwa średnik dwa koniec nawiasu.

Jeżeli chcemy naszkicować parabolę, będącą wykresem funkcji kwadratowej określonej wzorem w postaci kanonicznej $f (x) = a {(x - p)}^{2} + q$ , gdzie $a, p, q \in ℝ$ oraz $a \neq 0$ , to ze wzoru funkcji warto odczytać następujące własności:

dla $a > 0$ ramiona paraboli są skierowane do góry, dla $a < 0$ ramiona paraboli są skierowane do dołu,
dla $a > 0$ zbiorem wartości funkcji $f$ jest przedział $⟨q, \infty)$ , dla $a < 0$ zbiorem wartości funkcji jest przedział $(- \infty, q⟩$ ,
wierzchołkiem wykresu funkcji $f$ jest punkt o współrzędnych $W = (p, q)$ ,
osią symetrii wykresu funkcji $f$ jest prosta o równaniu $x = p$ ,
dla $a > 0$ funkcja $f$ jest malejąca w przedziale $(- \infty, p⟩$ oraz rosnąca w przedziale $⟨p, \infty)$ ,
dla $a < 0$ funkcja $f$ jest rosnąca w przedziale $(-\infty, p⟩$ oraz malejąca w przedziale $⟨p, \infty)$ .

Ważne!

Wykres przedstawiony na rysunku możemy otrzymać poprzez przesunięcie wykresu funkcji określonej wzorem $g (x) = - 2 x^{2}$ o $3$ jednostki w lewo wzdłuż osi $X$ oraz o $4$ jednostki w górę wzdłuż osi $Y$ .

Punkt przecięcia wykresu każdej funkcji kwadratowej $f$ z osią $Y$ ma współrzędne $(0, f (0))$ .

Przykład 1

Dana jest funkcja kwadratowa określona wzorem $f (x) = - 3 {(x + 2)}^{2} - 4$ . Wyznaczymy:

a) współrzędne wierzchołka paraboli, która jest wykresem tej funkcji,

b) oś symetrii paraboli, która jest wykresem tej funkcji,

c) przedziały monotoniczności tej funkcji.

Rozwiązanie:

a) Wierzchołek tej paraboli ma współrzędne $(- 2, - 4)$ .

b) Ze wzoru funkcji możemy odczytać, że pierwsza współrzędna wierzchołka paraboli, która jest wykresem funkcji to $p = - 2$ , zatem osią symetrii paraboli, która jest wykresem tej funkcji, jest prosta o równaniu $x = - 2$ .

c) Ponieważ $a = - 3$ , zatem ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu.

Zatem funkcja jest:

rosnąca w przedziale $(- \infty, - 2⟩$ ,
malejąca w przedziale $⟨- 2, \infty)$ .

Mając dany wykres funkcji kwadratowej, możemy wyznaczyć wzór tej funkcji.

Przykład 2

Na rysunku przedstawiono wykres funkcji kwadratowej określonej wzorem $f (x) = a {(x - p)}^{2} + q$ .

RBMBsFyFE1CjK

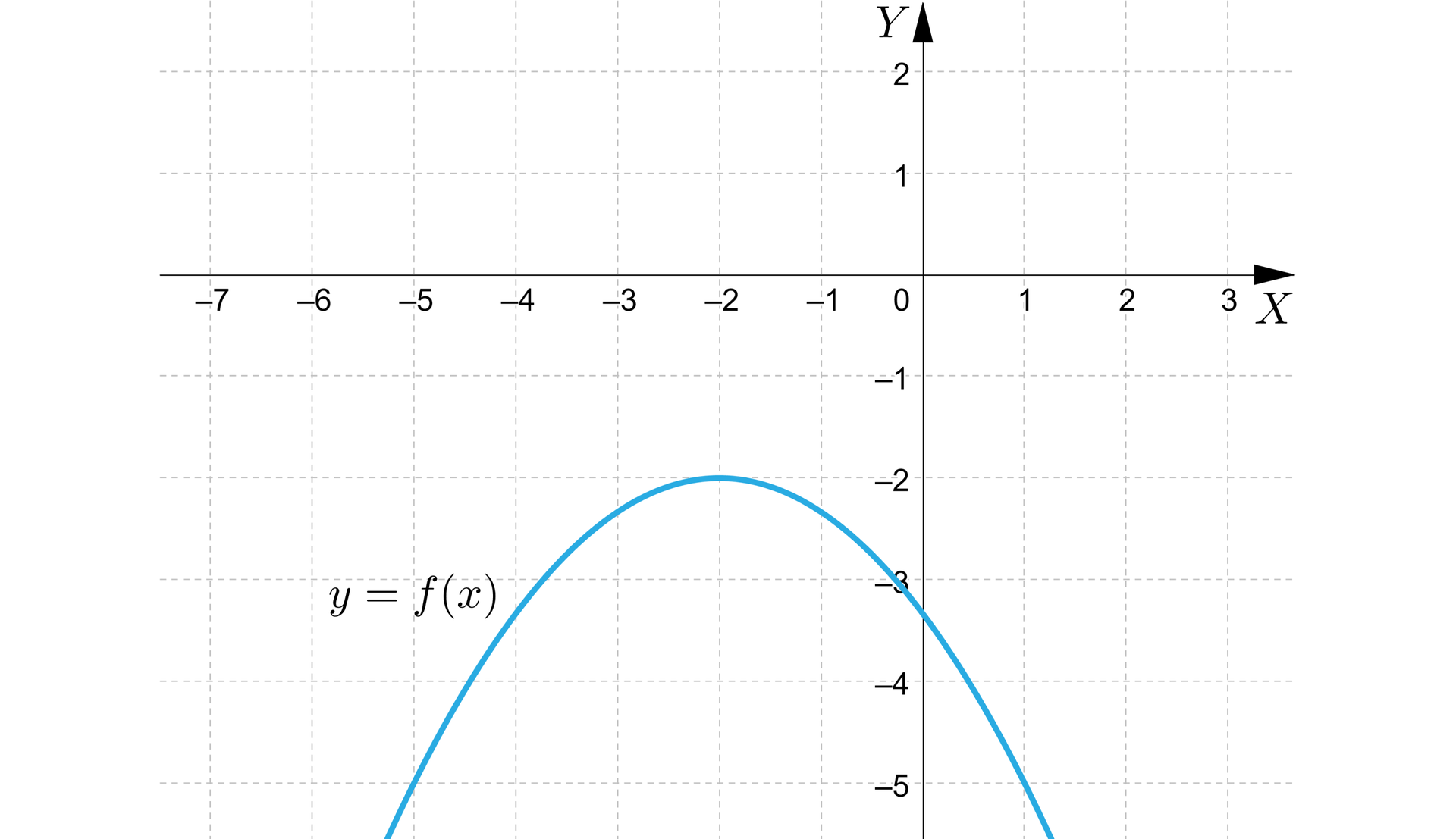
Ilustracja przedstawia poziomą oś X od minus siedmiu do trzech i pionową oś Y od minus pięciu do dwóch. Na rysunku zaznaczono także wykres funkcji kwadratowej będącej parabola z ramionami skierowanymi w dół i wierzchołkiem w punkcie nawias minus dwa średnik minus dwa. Wykres funkcji przechodzi przez punkty nawias minus pięć średnik minus pięć koniec nawiasu oraz nawias jeden średnik minus pięć koniec nawiasu.

Wyznaczymy wzór tej funkcji.

Rozwiązanie:

Zauważmy, że prosta o równaniu $x = - 2$ jest osią symetrii tej paraboli, zatem $p = - 2$ .

Zbiorem wartości funkcji jest przedział $(- \infty, - 2⟩$ , zatem $q = - 2$ .

Wzór funkcji możemy zapisać w postaci $f (x) = a {(x + 2)}^{2} - 2$ .

Z wykresu funkcji odczytujemy, że należy do niego punkt o współrzędnych $(1, - 5)$ .

Zatem aby wyznaczyć wartości współczynnika $a$ , rozwiązujemy równanie:

$- 5 = a \cdot {(1 + 2)}^{2} - 2$ , więc $a = - \frac{1}{3}$ .

Wzór funkcji przedstawionej na rysunku jest postaci $f (x) = - \frac{1}{3} {(x + 2)}^{2} - 2$ .

Jeżeli mamy dane współrzędne punktu, który należy do wykresu funkcji kwadratowej oraz przedziały monotoniczności lub równanie osi symetrii jej wykresu, wówczas możemy wyznaczyć wzór tej funkcji.

Przykład 3

Wykres funkcji kwadratowej określonej wzorem $f (x) = a {(x - p)}^{2} + q$ spełnia następujące warunki:

do wykresu należy punkt o współrzędnych $(5, 1)$ ,
osią symetrii paraboli, która jest wykresem tej funkcji, jest prosta o równaniu $x = 3$ ,
zbiorem wartości funkcji jest przedział $⟨- 1, \infty)$ .

Wyznaczymy wzór tej funkcji.

Rozwiązanie:

Ponieważ osią symetrii paraboli, która jest wykresem tej funkcji, jest prosta o równaniu $x = 3$ , zatem $p = 3$ .

Jeżeli zbiorem wartości funkcji jest przedział $⟨- 1, \infty)$ , to $q = - 1$ .

Zatem wzór tej funkcji zapisujemy w postaci $f (x) = a {(x - 3)}^{2} - 1$ .

Ponieważ punkt o współrzednych $(5, 1)$ należy do wykresu tej funkcji, zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$1 = a \cdot {(5 - 3)}^{2} - 1$ .

Zatem $a = \frac{1}{2}$ .

Wzór tej funkcji zapisujemy w postaci $f (x) = \frac{1}{2} {(x - 3)}^{2} - 1$ .

Przykład 4

Dana jest funkcja kwadratowa określona wzorem $f (x) = - 3 x^{2} + 6 x + 1$ .

Wyznaczymy:

a) równanie osi symetrii wykresu tej funkcji,

b) współrzędne wierzchołka paraboli, która jest wykresem tej funkcji,

c) przedziały monotoniczności tej funkcji.

Rozwiązanie:

Zauważmy, że wzór funkcji możemy zapisać w nastepującej postaci:

$f (x) = - 3 x^{2} + 6 x + 1 = - 3 (x^{2} - 2 x + 1) + 4 = - 3 {(x - 1)}^{2} + 4$ .

a) Ze wzoru funkcji możemy odczytać, że $p = 1$ , zatem osią symetrii paraboli, która jest wykresem tej funkcji jest prosta o równaniu $x = 1$ .

b) Wierzchołek paraboli, która jest wykresem tej funkcji ma współrzedne $(1, 4)$ .

c) Ponieważ $a = - 3$ , zatem ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu.

Funkcja jest:

rosnąca w przedziale $(- \infty, 1⟩$ ,
malejąca w przedziale $⟨1, \infty)$ .

Przykład 5

Określimy liczbę rozwiązań równania $f (x) = m$ , dla $m \in ℝ$ , gdy $f (x) = - 2 {(x + 5)}^{2} + 3$ .

Rozwiązanie:

Ponieważ $a = - 2$ , zatem ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu. Współrzędne wierzchołka tej funkcji wynoszą $(- 5, 3)$ .

Zatem równanie $f (x) = m$ , dla $m \in ℝ$ ma:

dwa rozwiązania, gdy $(- \infty, 3)$ ,
jedno rozwiązanie, gdy $m = 3$ ,
zero rozwiązań, gdy $m \in (3, \infty)$ .

Słownik

wzór funkcji kwadratowej w postaci kanonicznej

f (x) = a {(x - p)}^{2} + q

gdzie:

$p = \frac{- b}{2 a}$

$q = \frac{- ∆}{4 a}$

$∆ = b^{2} - 4 a c$

parabola

wykres funkcji kwadratowej

Wprowadzenie

Aplet

Słownik