Aplet
Polecenie 1
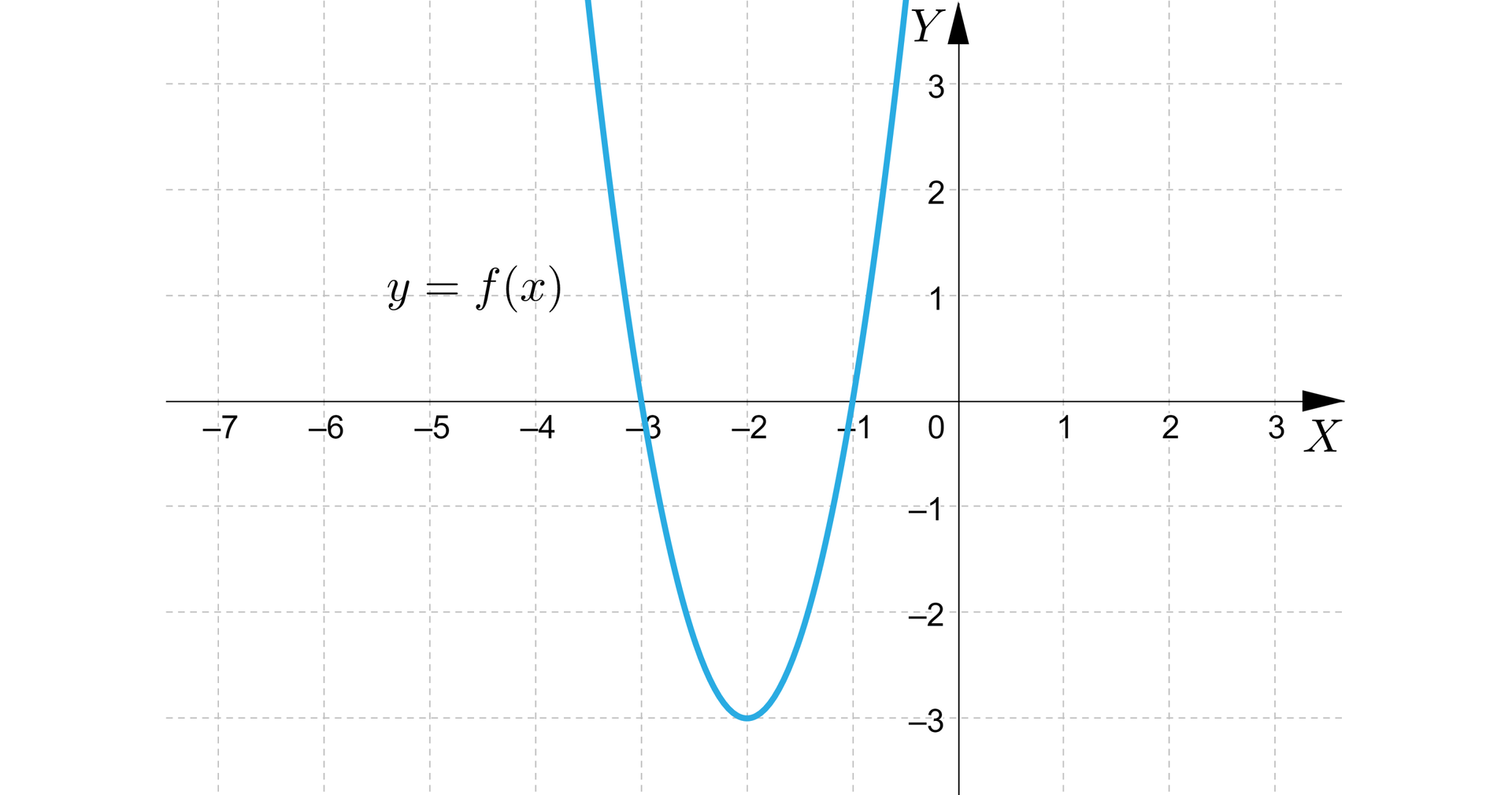
Uruchom aplet, a następnie wykonaj poniższe polecenie. Zwróć uwagę na współrzędne wierzchołka paraboli oraz własności funkcji, które można odczytać za pomocą wykresu.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DoB1uSdbq
Polecenie 2
Narysuj wykres funkcji kwadratowej określonej wzorem i określ kilka własności tej funkcji.