Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na poniższym rysunku przedstawiono parabolę.

R14aOP2qrbcf6

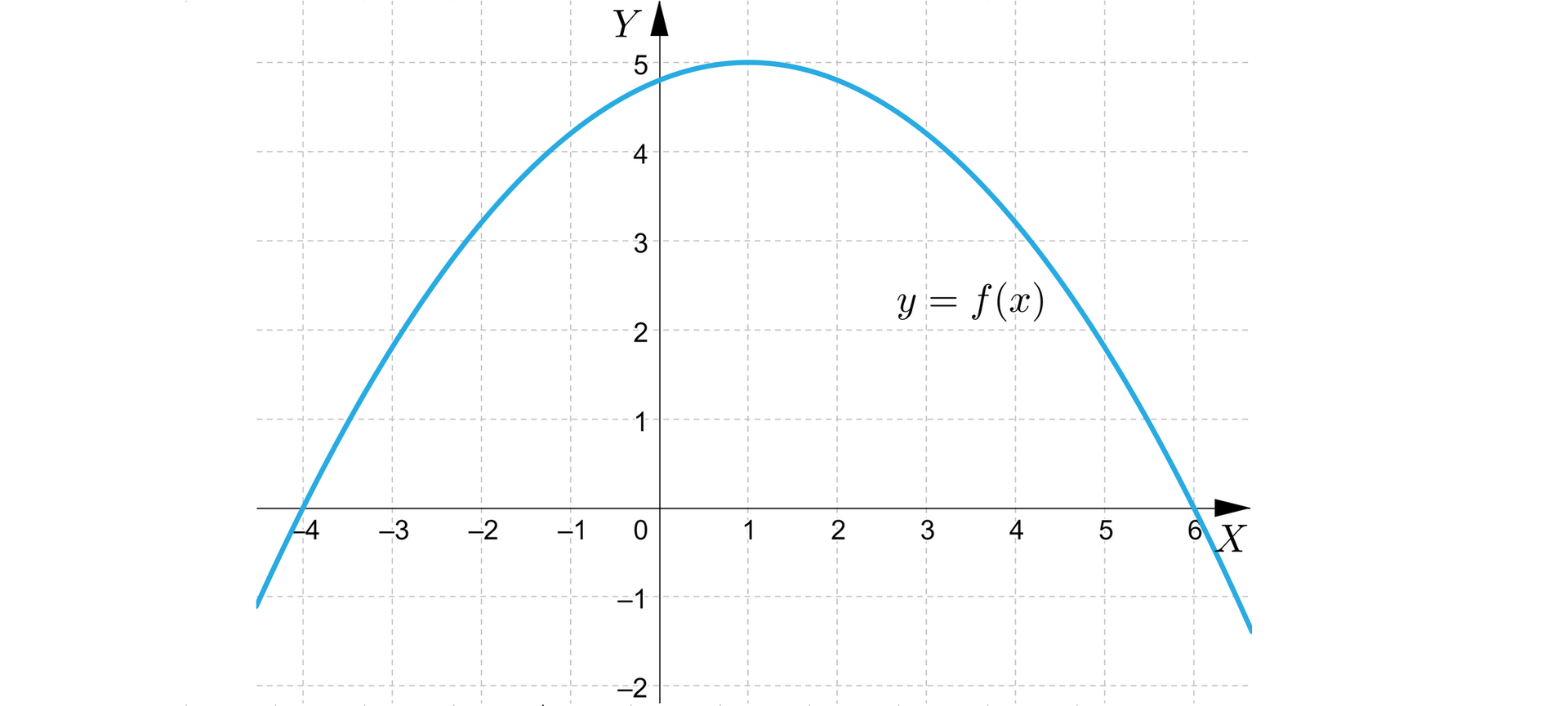
Ilustracja przedstawia poziomą oś X od minus czterech do sześciu i pionową oś Y od minus dwóch do pięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będący parabolą z ramionami skierowanymi w dół i z wierzchołkiem w punkcie nawias jeden średnik pięć. Wykres funkcji posiada dwa miejsca zerowe w punktach nawias minus cztery średnik zero koniec nawiasu i w punkcie nawias sześć średnik zero koniec nawiasu.

RgECV9UWZov13

Ćwiczenie 2

R2wjJ3V7dFZ8J

RJVspQQFE8uce

Dopasuj wzór do odpowiadającego mu wykresu funkcji kwadratowej.

f (x) = 2 {(x - 1)}^{2} - 3

Możliwe odpowiedzi: 1. Ilustracja przedstawia poziomą oś X od minus sześciu do dwóch i pionową oś Y od minus cztery do cztery. Na rysunku zaznaczono także wykres funkcji kwadratowej będący parabolą z ramionami skierowanymi w dół i wierzchołkiem w punkcie nawias minus dwa średnik cztery. Wykres funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias minus trzy średnik jeden koniec nawiasu oraz nawias minus jeden średnik jeden koniec nawiasu., 2. Ilustracja przedstawia poziomą oś X od minus dwóch do sześciu i pionową oś Y od minus cztery do cztery. Na rysunku zaznaczono także wykres funkcji kwadratowej będący parabolą z ramionami skierowanymi w górę i wierzchołkiem w punkcie nawias trzy średnik minus cztery. Wykres funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias dwa średnik minus jeden koniec nawiasu oraz nawias cztery średnik minus jeden koniec nawiasu., 3. Ilustracja przedstawia poziomą oś X od minus trzech do pięciu i pionową oś Y od minus cztery do cztery. Na rysunku zaznaczono także wykres funkcji kwadratowej będący parabolą z ramionami skierowanymi w górę i wierzchołkiem w punkcie nawias jeden średnik minus trzy. Wykres funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias zero średnik minus jeden koniec nawiasu oraz nawias dwa średnik minus jeden koniec nawiasu.

f (x) = - 3 {(x + 2)}^{2} + 4

f (x) = 3 {(x - 3)}^{2} - 4

Dopasuj wzór do odpowiadającego mu wykresu funkcji kwadratowej.

f (x) = 2 {(x - 1)}^{2} - 3

f (x) = - 3 {(x + 2)}^{2} + 4

f (x) = 3 {(x - 3)}^{2} - 4

Ćwiczenie 3

Na poniższym rysunku przedstawiono wykres funkcji kwadratowej.

Rm4U81KnDZxc9

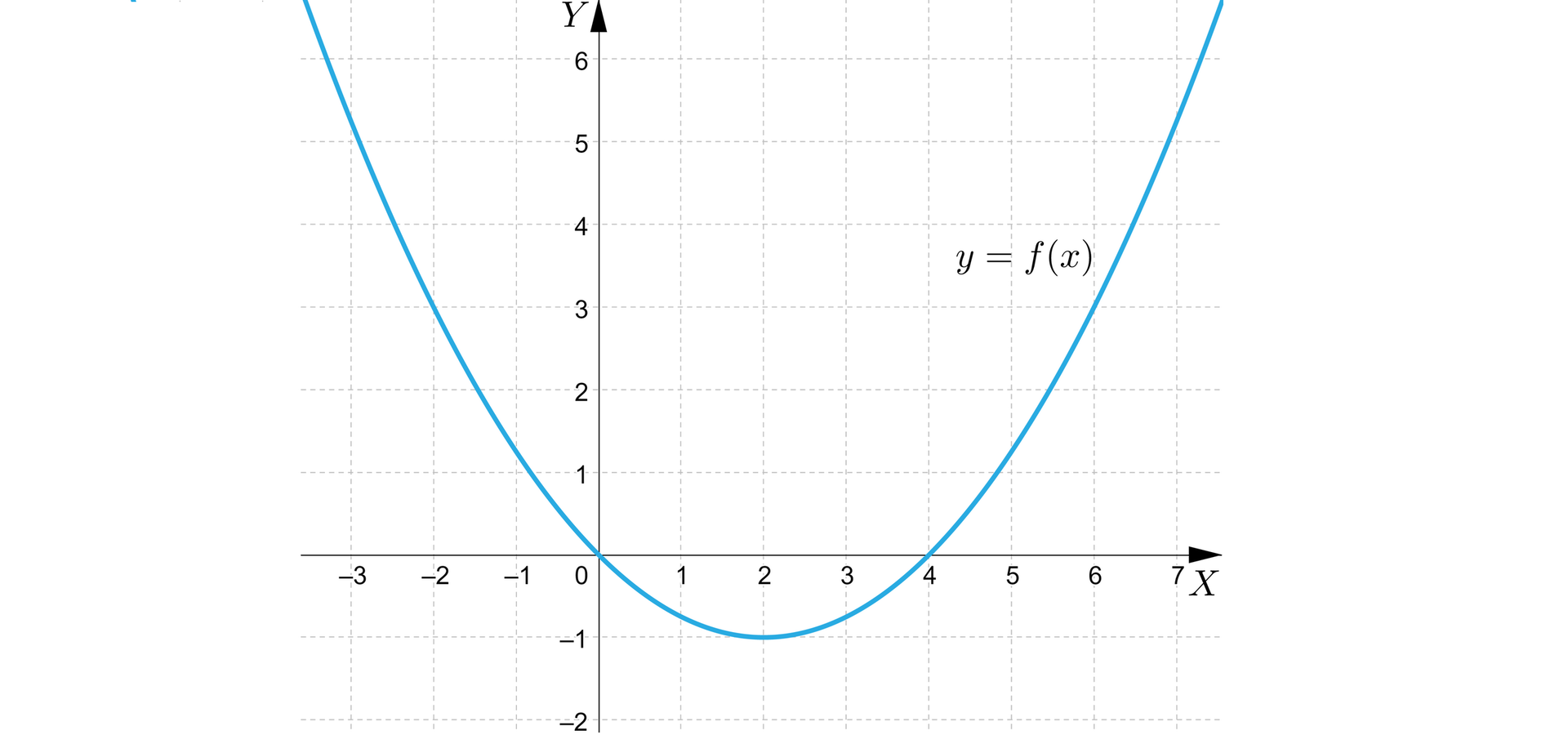
Ilustracja przedstawia poziomą oś X od minus trzech do siedmiu i pionową oś Y od minus dwóch do pięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będący parabolą z ramionami skierowanymi w górę i wierzchołkiem w punkcie nawias dwa średnik minus jeden koniec nawiasu. Wykres funkcji posiada dwa miejsca zerowe w punktach nawias zero średnik zero koniec nawiasu i w punkcie nawias cztery średnik zero koniec nawiasu.

R9UANwfFD0edg

Ćwiczenie 4

Na rysunku przedstawiono wykresy oznaczone odpowiednio: $I$ i $II$ .

Na rysunku przedstawiono wykresy oznaczone odpowiednio: jedynką rzymską i dwójką rzymską.

R1NNNGxpC34Rf

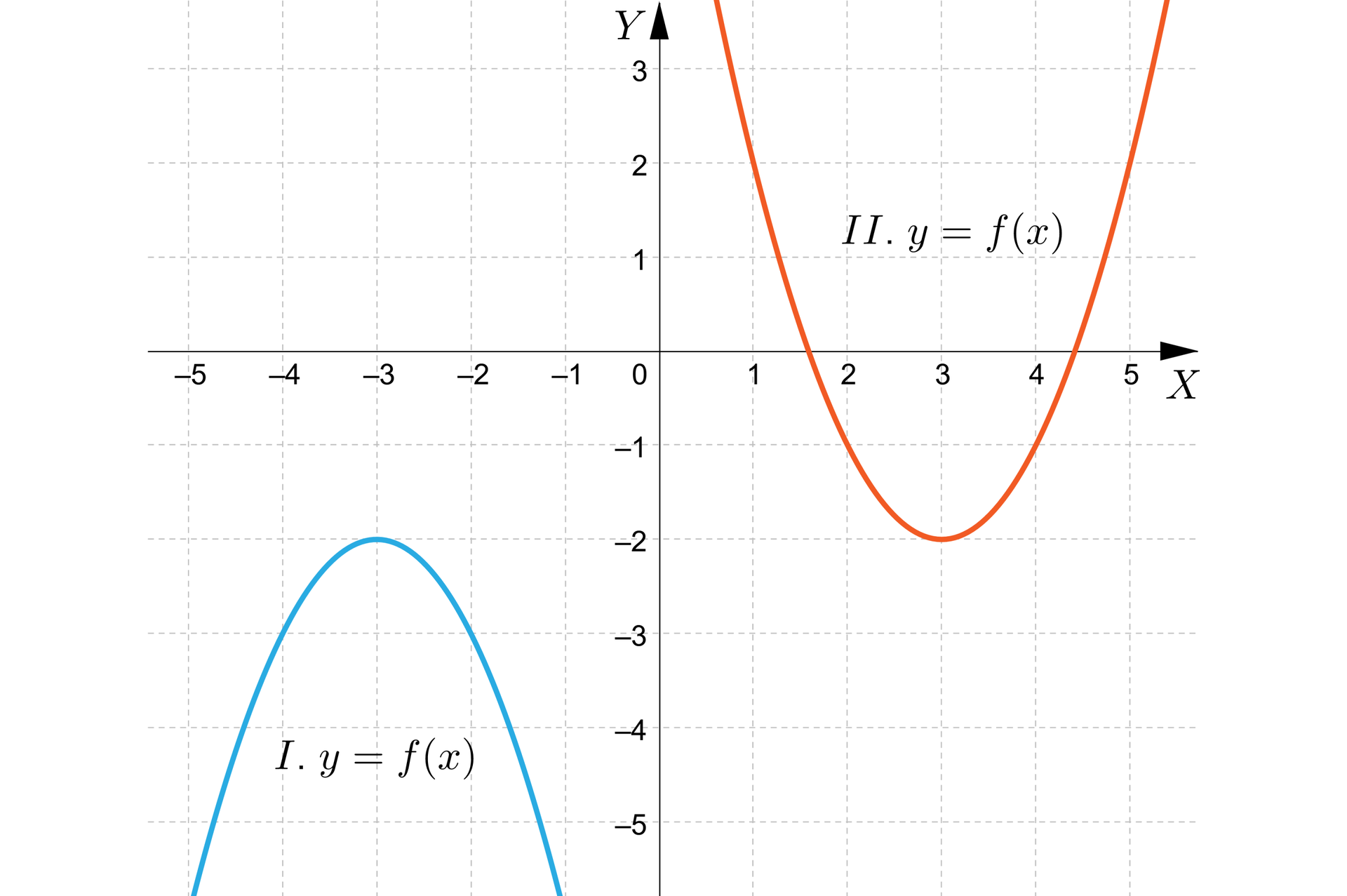
Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu i pionową oś Y od minus pięciu do trzech. Na rysunku zaznaczono także wykresy dwóch funkcji kwadratowych będące parabolami. Parabola oznaczona jedynką rzymską posiada ramiona skierowane w dół i wierzchołek w punkcie nawias minus trzy średnik minus dwa koniec nawiasu. Wykres funkcji przechodzi przez punkty nawias minus cztery średnik minus trzy koniec nawiasu i punkt nawias minus dwa średnik minus trzy koniec nawiasu. Parabola oznaczona dwójką rzymską posiada wierzchołek w puncie nawias trzy średnik minus dwa oraz ramiona skierowane w górę. Wykres drugiej funkcji posiada dwa miejsca zerowe i przechodzi przez punkty nawias jeden średnik dwa koniec nawiasu oraz nawias pięć średnik dwa koniec nawiasu.

Rqi0me6C1FQlo

Przyporządkuj własności do wykresów funkcji. Własności wykresu

I

: Możliwe odpowiedzi: 1. funkcję przedstawioną na rysunku można zapisać za pomocą wzoru

f (x) = - {(x + 3)}^{2} - 2

, 2. wierzchołek wykresu ma współrzędne

(- 3, - 2)

, 3. osią symetrii wykresu jest prosta o równaniu

x = 3

, 4. funkcję przedstawioną na rysunku można zapisać za pomocą wzoru

f (x) = {(x - 3)}^{2} - 2

, 5. wierzchołek wykresu ma współrzędne

(3, - 2)

, 6. osią symetrii wykresu jest prosta o równaniu

x = - 3

. Własności wykresu

II

: Możliwe odpowiedzi: 1. funkcję przedstawioną na rysunku można zapisać za pomocą wzoru

f (x) = - {(x + 3)}^{2} - 2

, 2. wierzchołek wykresu ma współrzędne

(- 3, - 2)

, 3. osią symetrii wykresu jest prosta o równaniu

x = 3

, 4. funkcję przedstawioną na rysunku można zapisać za pomocą wzoru

f (x) = {(x - 3)}^{2} - 2

, 5. wierzchołek wykresu ma współrzędne

(3, - 2)

, 6. osią symetrii wykresu jest prosta o równaniu

x = - 3

Przyporządkuj własności do wykresów funkcji.

osią symetrii wykresu jest prosta o równaniu <math><mi>x</mi><mo>=</mo><mn>3</mn></math>, wierzchołek wykresu ma współrzędne <math><mfenced><mrow><mo>-</mo><mn>3</mn><mo>,</mo><mo>-</mo><mn>2</mn></mrow></mfenced></math>, wierzchołek wykresu ma współrzędne <math><mfenced><mrow><mn>3</mn><mo>,</mo><mo>-</mo><mn>2</mn></mrow></mfenced></math>, osią symetrii wykresu jest prosta o równaniu <math><mi>x</mi><mo>=</mo><mo>-</mo><mn>3</mn></math>., funkcję przedstawioną na rysunku można zapisać za pomocą wzoru <math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><msup><mfenced><mrow><mi>x</mi><mo>-</mo><mn>3</mn></mrow></mfenced><mn>2</mn></msup><mo>-</mo><mn>2</mn></math>, funkcję przedstawioną na rysunku można zapisać za pomocą wzoru <math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mo>-</mo><msup><mfenced><mrow><mi>x</mi><mo>+</mo><mn>3</mn></mrow></mfenced><mn>2</mn></msup><mo>-</mo><mn>2</mn></math>

Własności wykresu $I$ :
Własności wykresu $II$ :

RdQUjlh8vCJeG2

Ćwiczenie 5

Wstaw w tekst odpowiednie liczby.

$4$ , $3$ , $- 3$ , $1$

Funkcja kwadratowa jest określona wzorem $f (x) = - 3 x^{2} + 6 x$ .
Wtedy:
- wierzchołek paraboli, która jest wykresem tej funkcji, ma współrzędne $($ ............ $,$ ............ $)$ ,
- postacią kanoniczną wzoru funkcji jest $f (x) =$ ............ $\cdot {(x - 1)}^{2} + 3$ ,
- równanie $f (x) =$ ............ nie ma rozwiązania.

R1P88nnviIbBA2

Ćwiczenie 6

Uzupełnij tekst odpowiednimi liczbami.

Wykresem funkcji kwadratowej jest parabola o wierzchołku $(2, - 3)$ , przechodząca przez punkt o współrzędnych $(1, 0)$ . Zatem:
- postać kanoniczną wzoru funkcji zapisujemy jako $f (x) =$ ............ $\cdot {(x - 2)}^{2} - 3$ ,
- osią symetrii tego wykresu jest prosta o równaniu $x =$ ............,
- zbiorem wartości funkcji jest przedział $⟨$ ............ $, \infty)$ .

Ćwiczenie 7

Wykresem funkcji kwadratowej jest parabola o wierzchołku w punkcie $(1, 2)$ . Wyznacz wzór tej funkcji w postaci kanonicznej, jeżeli wiadomo, że do wykresu tej funkcji należy punkt o współrzędnych $(3, - 4)$ .

Jeżeli wierzchołkiem paraboli, która jest wykresem tej funkcji, jest punkt o współrzędnych $(1, 2)$ , to wzór funkcji w postaci kanonicznej zapisujemy jako $f (x) = a \cdot {(x - 1)}^{2} + 2$ .

Ponieważ do wykresu tej funkcji należy punkt o współrzędnych $(3, - 4)$ , zatem, aby wyznaczyć wartość $a$ , rozwiązujemy równanie:

$- 4 = a \cdot {(3 - 1)}^{2} + 2$ .

Zatem $a = - \frac{3}{2}$ .

Wobec tego wzór funkcji w postaci kanonicznej zapisujemy jako $f (x) = - \frac{3}{2} {(x - 1)}^{2} + 2$ .

Ćwiczenie 8

Zapisz wzór funkcji $f (x) = - x^{2} + x$ w postaci kanonicznej, a następnie podaj:

zbiór wartości,
przedziały monotoniczności tej funkcji.

Obliczamy:

$p = \frac{- 1}{2 \cdot (- 1)} = \frac{1}{2}$ ,

$q = f (\frac{1}{2}) = - {(\frac{1}{2})}^{2} + \frac{1}{2} = \frac{1}{4}$ .

Zauważmy, że $a = - 1$ , zatem ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu.

Postać kanoniczna wyraża się wzorem $f (x) = - {(x - \frac{1}{2})}^{2} + \frac{1}{4}$ .

Zbiorem wartości funkcji jest przedział $(- \infty, \frac{1}{4}⟩$ .
Funkcja jest:
- rosnąca w przedziale $(- \infty, \frac{1}{2}⟩$ ,
- malejąca w przedziale $⟨\frac{1}{2}, \infty)$ .

Aplet

Dla nauczyciela