Przeczytaj

Na lekcji zapoznamy się z przykładami nierówności z funkcją tangens. Będziemy w szczególności rozwiązywać nierówności z wartością bezwzględną. Przypomnijmy zatem, jak rozwiązujemy takie nierówności.

Podstawową metodą jest rozważanie przypadków.

Zatem każdą wartość bezwzględną rozważamy w dwóch przypadkach w zależności od tego, jakiego znaku jest wyrażenie znajdujące się pod wartością bezwzględną.

Na przykład wyrażenie $| 2 x - 3 |$ można zapisać następująco:

$2 x - 3$ dla $x \geq \frac{3}{2}$

oraz

$3 - 2 x$ dla $x < \frac{3}{2}$ .

Przykład 1

Rozwiążemy nierówność $tg 2 x tg (\frac{π}{2} + x) \geq 0$ .

Rozwiązanie

Zapiszmy założenia.

Aby istniał $tg 2 x$ : $x \neq \frac{π}{4} + \frac{k π}{2}$ , gdzie $k \in ℤ$ .

Aby istniał $tg (\frac{π}{2} + x)$ : $\frac{π}{2} + x \neq \frac{π}{2} + k π$ , gdzie $k \in ℤ$ .

Rysujemy dwa wykresy funkcji $y = tg 2 x$ oraz $y = tg (\frac{π}{2} + x)$ i odczytujemy dla jakich argumentów we wspólnej dziedzinie funkcje $y = tg 2 x$ i $y = tg (\frac{π}{2} + x)$ mają ten sam znak lub jedna z nich przyjmuje wartość $0$ .

Wykres funkcji $y = tg 2 x$ otrzymujemy przekształcając wykres funkcji $y = tg x$ w powinowactwie o osi $Y$ i skali $\frac{1}{2}$ .

Wykres funkcji $y = t g (\frac{π}{2} + x)$ otrzymujemy przekształcając wykres funkcji $y = tg x$ w przesunięciu o wektor $[- \frac{π}{2}, 0]$ .

Okresem zasadniczym funkcji $y = tg 2 x$ jest $T_{1} = \frac{π}{2}$ . Okresem zasadniczym funkcji $y = tg (\frac{π}{2} + x)$ jest $T_{2} = π$ . Zatem możemy rozwiązać nierówność na przedziale o długości $π$ np. $(0, π⟩$ , a następnie uogólnić na całą dziedzinę.

R16lCkwVkOexU

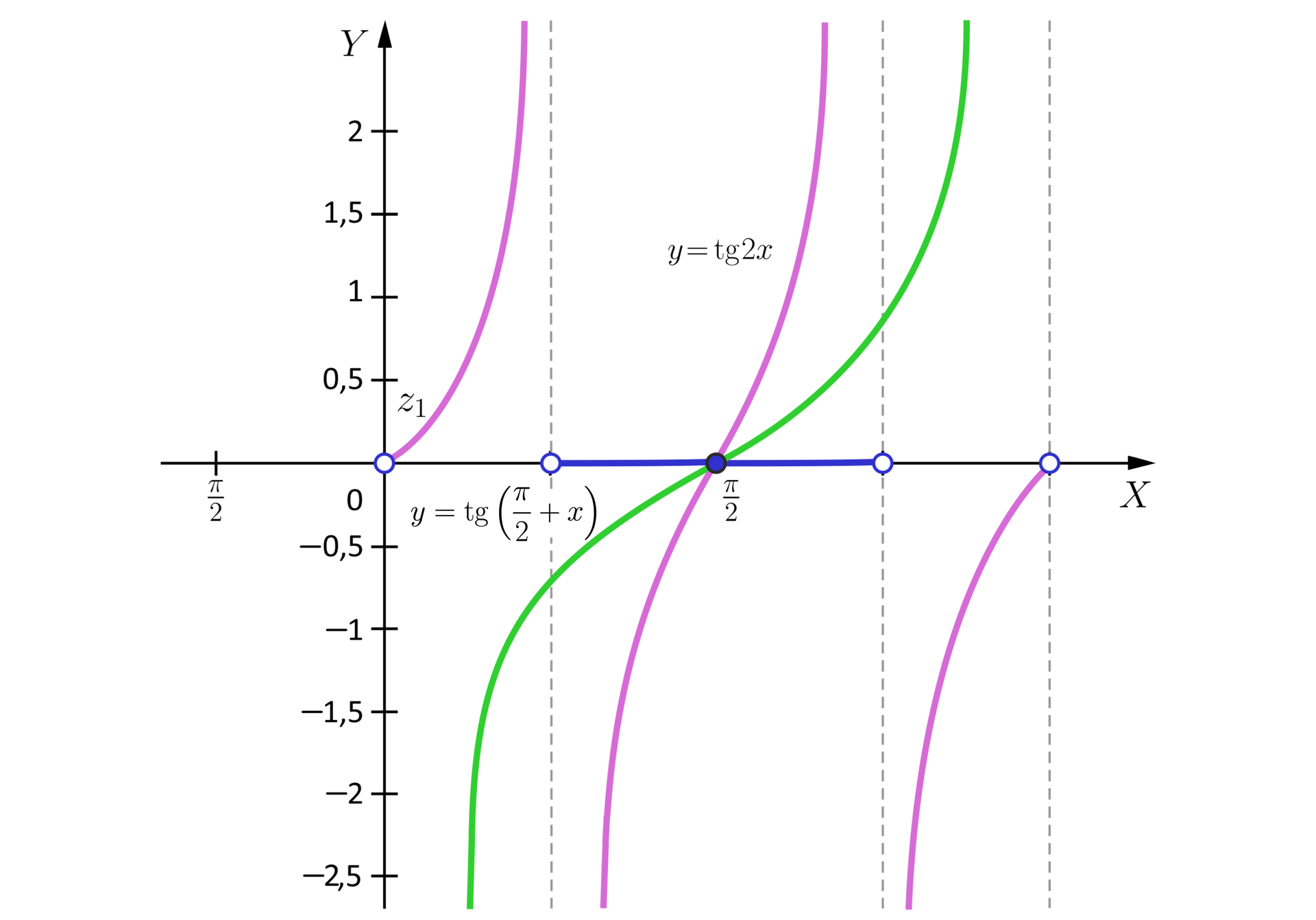
Rysunek przedstawia układ współrzędnych z poziomą osią X od minus pi drugich do pi oraz z pionową osią Y od minus trzech do dwóch. Na płaszczyźnie narysowany jest wykres funkcji y=tg2x oraz wykres funkcji y=tgπ2+x. Okresem zasadniczym pierwszej funkcji jest T1=π2, natomiast okresem funkcji drugiej jest T2=π. Oba wykresy przecinają się w punkcie π2; 0. Na poziomej osi X pogrubioną linią zaznaczono przedział π4; 3π4 będącym jednym z możliwych rozwiązań nierówności.

Z wykresów odczytujemy rozwiązanie nierównościrozwiązanie nierównościrozwiązanie nierówności $(\frac{π}{4} + k π, \frac{3 π}{4} + k π)$ , gdzie $k \in ℤ$ .

Przykład 2

Rozwiążemy nierówność $tg (π - x) |tg x| > 3$ .

Rozwiązanie

Najpierw, korzystając ze wzorów redukcyjnych zapiszmy, że $tg (π - x) = - tg x$ .

Nierówność przyjmuje postać $- tg x |tg x| > 3$ , czyli $tg x |tg x| < - 3$ .

Zauważmy, że jeżeli $tg x \geq 0$ , to nierówność nie jest spełniona dla żadnego argumentu.

Jeżeli $tg x < 0$ , to nierówność z zadania przyjmuje postać ${tg}^{2} x > 3$ . Zatem w połączeniu z założeniem $tg x < 0$ otrzymujemy nierówność $tg x < - \sqrt{3}$ .

Zatem rozwiązaniem jest zbiór $(- \frac{π}{2} + k π, - \frac{π}{3} + k π)$ , gdzie $k \in ℤ$ .

Przykład 3

Rozwiążemy nierówność $|tg x + 2| < 2 tg x + 1$ .

Rozwiązanie

Rozważmy dwa przypadki.

Przypadek 1

Niech $tg x + 2 \geq 0$ .

Wówczas nierówność przyjmuje postać $tg x + 2 < 2 tg x + 1$ .

Po uwzględnieniu założenia $tg x + 2 \geq 0$ dostajemy $1 < tg x$ .

Rozwiązaniem nierówności w przypadku 1. jest zbiór $(\frac{π}{4} + k π, \frac{π}{2} + k π)$ , gdzie $k \in ℤ$ .

Przypadek 2

Niech $tg x + 2 < 0$ .

Wówczas nierówność przyjmuje postać $- tg x - 2 < 2 tg x + 1$ .

Dostajemy $- 3 < 3 tg x$ , czyli $- 1 < tg x$ .

Przy założeniu, że $tg x + 2 < 0$ otrzymujemy sprzeczność.

Zatem rozwiązaniem nierówności jest zbiór $(\frac{π}{4} + k π, \frac{π}{2} + k π)$ , gdzie $k \in ℤ$ .

W przykładzie 4 zaprezentujemy metodę podstawiania. Metodę tę stosujemy wtedy, gdy nierówność np. trygonometryczną możemy sprowadzić do nierówności wielomianowej poprzez podstawienie w miejsce funkcji trygonometrycznej nowej zmiennej. Oczywiście, po zakończeniu rozwiazywania nierówności z nową zmienną, należy rozwiązać odpowiednie proste nierówności trygonometryczne.

Przykład 4

Rozwiążemy nierówność $\frac{2 tg x}{1 - {tg}^{2} x} > \sqrt{3}$ .

Rozwiązanie

Przenieśmy wyrażenie z prawej strony nierówności i sprowadźmy do wspólnego mianownika

$\frac{2 tg x - \sqrt{3} (1 - {tg}^{2} x)}{1 - {tg}^{2} x} > 0$ .

Nierówność jest równoważna nierówności

$(\sqrt{3} {tg}^{2} x + 2 tg x - \sqrt{3}) (1 - {tg}^{2} x) > 0$ .

Podstawmy $t = tg x$ .

Otrzymujemy nierówność wielomianową

$(\sqrt{3} t^{2} + 2 t - \sqrt{3}) (1 - t^{2}) > 0$ .

Znajdujemy pierwiastki trójmianu $\sqrt{3} t^{2} + 2 t - \sqrt{3}$ .

$Δ = 4 + 4 \cdot \sqrt{3} \cdot \sqrt{3} = 16$

$t = \frac{- 2 - 4}{2 \sqrt{3}} = - \sqrt{3}$ lub $t = \frac{- 2 + 4}{2 \sqrt{3}} = \frac{\sqrt{3}}{3}$

Zatem wielomian $W (t) = (\sqrt{3} t^{2} + 2 t - \sqrt{3}) (1 - t^{2})$ ma pierwiastki $1$ , $(- 1)$ , $(- \sqrt{3})$ , $\frac{\sqrt{3}}{3}$ .

Rysujemy wykres wielomianu $W (t)$ .

RNW4gIZ2KqzyC

Rysunek przedstawia układ współrzędnych z poziomą osią X od minus dwóch do dwóch oraz z pionową osią Y od minus dwóch do jedynki. Na płaszczyźnie narysowany jest wykres funkcji wielomianowej o równaniu y=Wt. Wykres posiada cztery miejsca zerowe, t1=-3, t2=-1, t3=33 oraz t4=1. Funkcja przyjmuje wartości dodanie jedynie w dwóch przedziałach. Pierwszy -3; -1 oraz drugi 33; 1. Zbiorem wartości jest przedział -∞; 1,5.

Rozwiązaniem nierówności $(\sqrt{3} t^{2} + 2 t - \sqrt{3}) (1 - t^{2}) > 0$ jest zbiór $(- \sqrt{3}, - 1) \cup (\frac{\sqrt{3}}{3}, 1)$ .

Zatem $- \sqrt{3} < tg x < - 1$ lub $\frac{\sqrt{3}}{3} < tg x < 1$ .

Stąd otrzymujemy rozwiązanie nierówności $\frac{2 tg x}{1 - {tg}^{2} x} > \sqrt{3}$ , $(- \frac{π}{3} + k π, - \frac{π}{4} + k π) \cup (\frac{π}{6} + k π, \frac{π}{4} + k π)$ , gdzie $k \in ℤ$ .

Słownik

rozwiązanie nierówności

zbiór wszystkich elementów dziedziny nierówności, które spełniają tę nierówność

Wprowadzenie

Animacja

Słownik