Przeczytaj
Siedem mostów królewieckich
Narodziny teorii grafów datuje się na rok 1736. Jeden z głównych matematyków – Leonhard Euler – zaprezentował wtedy pracę, w której przedstawił problem siedmiu mostów królewieckich (Koenigsberg Bridge Problem – od nazwy miasta Koenigsberg, jak wówczas nazywał się Królewiec).
Królewiec (dzisiejszy Kaliningrad w Rosji) to miasto położone nad rzeką Pregołą. W jej rozwidleniach znajdują się dwie wyspy. W czasach Eulera, czyli w XVIII w., w obrębie miasta istniało siedem mostów – jeden łączył obie wyspy, a pozostałe łączyły wyspy z brzegami rzeki. Specyficzne ułożenie mostów stało się przyczynkiem do narodzin pewnej zagadki. Oto ona:
Czy można przejść kolejno przez wszystkie siedem mostów w taki sposób, by każdy z nich przekroczyć dokładnie raz i wrócić do miejsca startu?

W 1736 r. Euler przedstawił artykuł zawierający rozwiązanie problemu siedmiu mostów królewieckich. Stwierdził, że wybór ścieżki – na lądzie lub wyspie – nie ma znaczenia. Spostrzeżenie to pozwoliło przeformułować problem w sposób abstrakcyjny z zastosowaniem teorii grafów.

Euler użył wielkich liter alfabetu łacińskiego do reprezentowania lądów, a za pomocą małych liter oznaczył mosty.
W języku matematycznym zagadnienie dotyczące mostów królewieckich jest równoznaczne z pytaniem: Czy w grafie, którego wierzchołki odpowiadają lądom, a krawędzie – mostom, istnieje cyklcykl, który przechodzi przez każdą krawędź dokładnie raz?
Gdyby taki cykl istniał, moglibyśmy bez odrywania ołówka narysować graf, przechodząc po każdej krawędzi jeden raz. Takie figury nazywamy jednobieżnymi lub unikursalnymi.
Tak prezentuje się graf przedstawiający mosty i lądy w Królewcu z czasów Eulera:
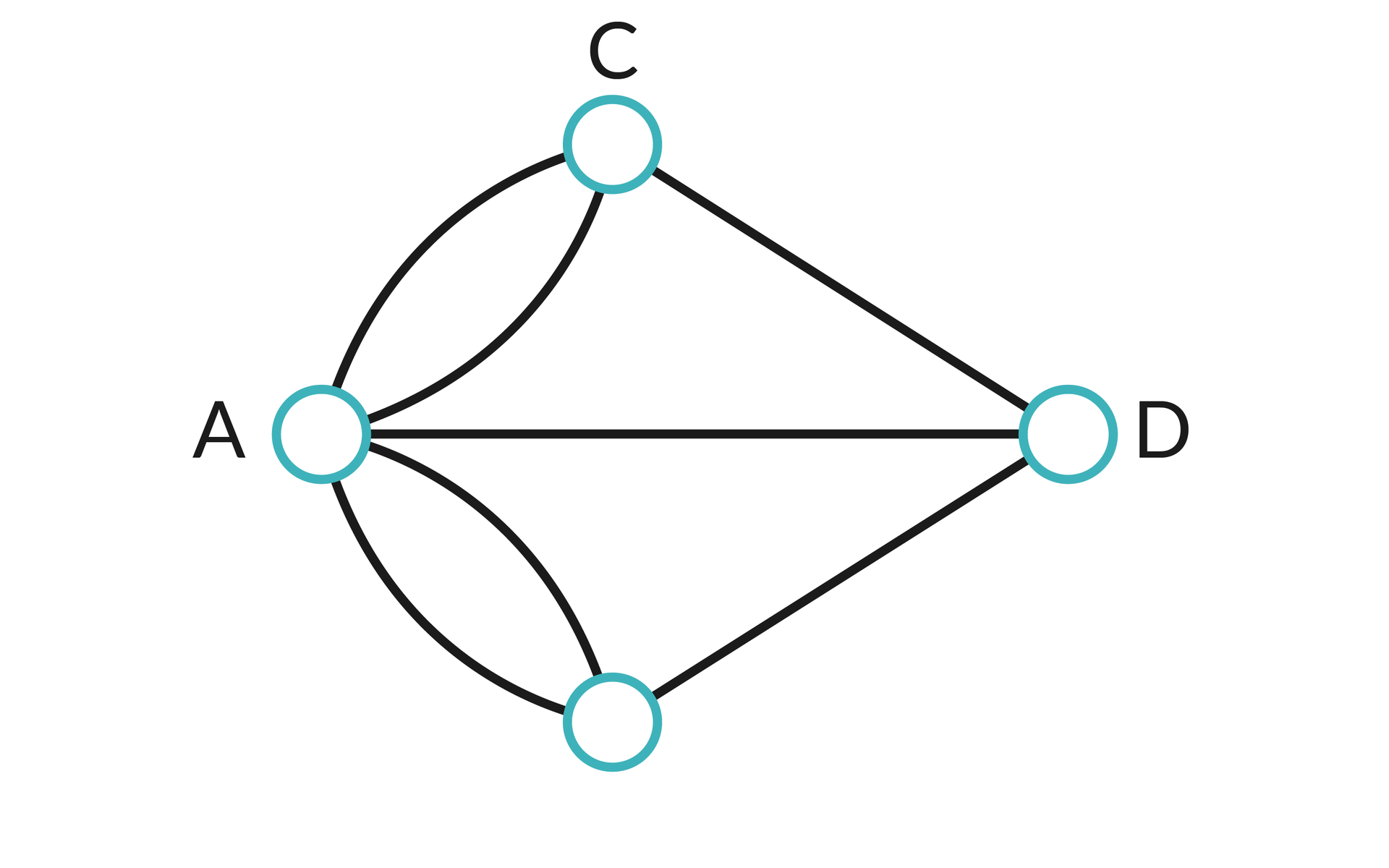
W teorii grafów taka ścieżkaścieżka zamknięta nazywana jest cyklem Eulera. Warunki istnienia takiego cyklu w grafie zostały przedstawione następującym twierdzeniem:
Spójny graf zawiera cykl Eulera wtedy i tylko wtedy, gdy każdy wierzchołek jest parzystego stopnia.
Wynika to z faktu, że za każdym razem, gdy wierzchołek zostanie odwiedzony przy przejściu przez jedną z krawędzi, przejście do kolejnego wierzchołka musi odbyć się inną krawędzią, aby pierwsza nie została powtórzona. Z tego powodu każdorazowe przejście przez wierzchołek w cyklu zwiększa liczbę odwiedzonych krawędzi o dwa. Oznacza to, że stopień każdego z wierzchołków musi być parzysty.
Warunkiem koniecznym istnienia cyklu Eulera jest spójność grafu. Gdyby graf nie był spójny, nie istniałaby możliwość odwiedzenia wszystkich jego wierzchołków w jednym cyklu.
Graf (będący multigrafemmultigrafem) przedstawiający problem mostów królewieckich zawiera cztery wierzchołki, z których każdy jest nieparzystego stopnia – zatem zgodnie z twierdzeniem, graf ten nie zawiera cyklu Eulera. Oznacza to, że nie można przejść przez siedem wspomnianych mostów w taki sposób, by każdy z nich przekroczyć dokładnie raz i wrócić do punktu początkowego.
Obecnie w Kaliningradzie (czyli dawnym Królewcu) na rzece Pregole istnieje pięć mostów, z czego tylko dwa pochodzą jeszcze z czasów Eulera. Gdyby przedstawić je za pomocą grafu, wówczas dwa węzły byłyby stopnia drugiego, a dwa pozostałe – stopnia trzeciego. Możliwe jest utworzenie ścieżki przechodzącej przez każdy z mostów jedynie raz, ale ze względu na nieparzyste stopnie dwóch wierzchołków nie będzie ona cyklem Eulera – zakończy się w innym wierzchołku niż wierzchołek początkowy.
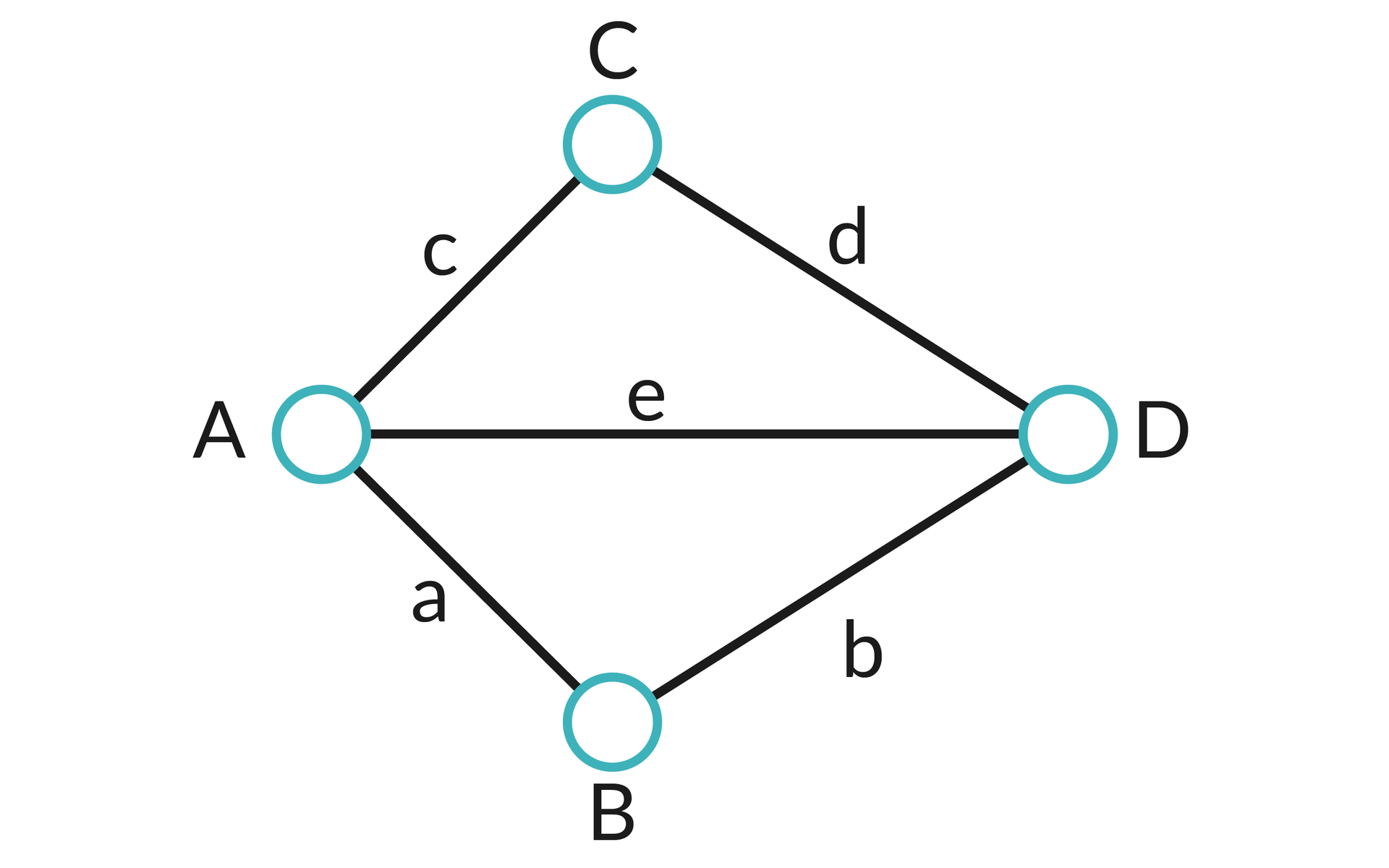
Algorytm sprawdzający, czy graf zawiera cykl Eulera – pseudokod
Wiemy już, że spójny graf zawiera cykl Eulera wtedy i tylko wtedy, gdy każdy wierzchołek jest parzystego stopnia. To, czy wierzchołki są parzystego stopnia, możemy odczytać z macierzy sąsiedztwa danego grafu.
Dla grafu przedstawiającego pięć mostów współczesnego Królewca macierz sąsiedztwa miałaby następującą postać:
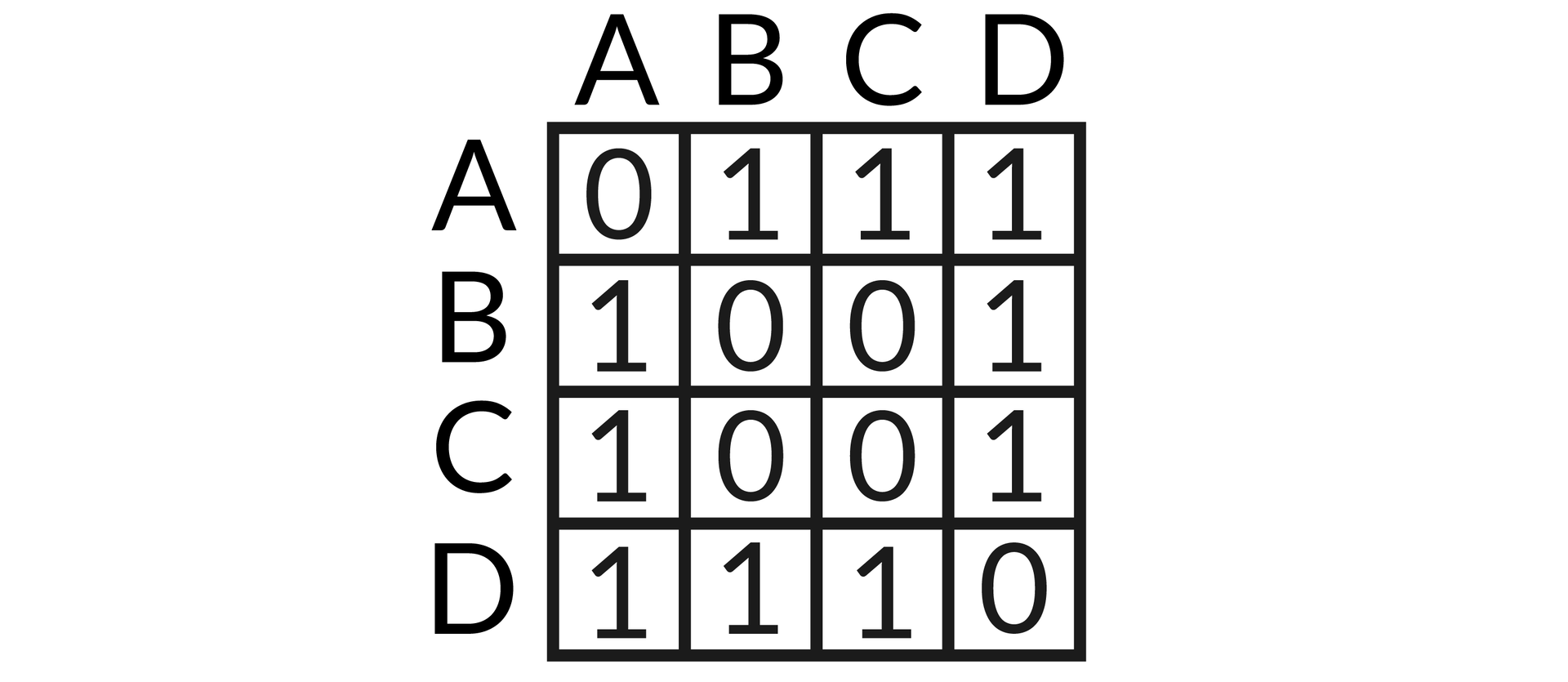
Poniżej znajduje się pseudokod funkcji sprawdzającej z użyciem macierzy sąsiedztwa, czy dany graf jest grafem eulerowskim. Jej argumentem jest macierz sąsiedztwa reprezentująca graf, na podstawie której sprawdzona zostanie parzystość stopni wierzchołków, oraz liczba wierzchołków grafu. Funkcja zwróci prawdziwy wynik jedynie w przypadku, gdy wejściowy graf jest spójny.
Specyfikacja problemu:
Dane:
macierzSasiedztwa– macierz sąsiedztwa grafu; tablica tablic (lista list) liczb naturalnych z przedziału <0,1>
Wynik:
komunikat informujący o tym, czy graf zawiera cykl Eulera
Zaczynamy od zapisania nagłówka funkcji istnienieCykluEulera, która jako argument przyjmuje macierz sąsiedztwa macierzSasiedztwa. W kolejnym kroku inicjalizujemy zmienną liczbaWierzcholkow jako rozmiar macierzy, czyli liczbę wierzchołków w grafie.
Następnie tworzymy tablicę (listę) stopnieWierzcholkow o długości liczbaWierzcholkow i wypełniamy ją wartościami początkowymi 0. Tworzymy również zmienną liczbaNieparzystych, której przypisujemy wartość 0. Zmienna będzie przechowywać liczbę wierzchołków o stopniu nieparzystym.
Zapisujemy pętlę, która będzie iterować po kolejnych wierzchołkach i zapisywać ich stopnie wierzchołków.
Wewnątrz tej pętli zapisujemy drugą pętlę, której zadaniem będzie sprawdzenie sąsiedztwa wierzchołka.
Dla każdego elementu tablicy (listy) stopnieWierzcholkow dodajemy wartość zmiennej macierzSasiedztwa[i][j] do wartości stopnia wierzchołka.
Po zakończeniu obu pętli obliczone zostają stopnie wszystkich wierzchołków.
Uruchamiamy pętlę, aby zliczyć wierzchołki o stopniu nieparzystym.
Sprawdzamy warunek stopnieWierzcholkow[i] mod 2 != 0. Jeśli warunek jest spełniony, zwiększamy wartość zmiennej liczbaNieparzystych o 1.
Po zakończeniu pętli zostaje obliczona liczba wierzchołków o stopniu nieparzystym.
Wykonujemy instrukcję warunkową. Sprawdzamy, czy wartość zmiennej liczbaNieparzystych wynosi 0 oraz czy wartość zmiennej liczbaWierzcholkow jest większa od 0. Jeśli tak, oznacza to, że wszystkie wierzchołki mają stopień parzysty, a więc graf zawiera cykl Eulera. Wypisujemy odpowiedni komunikat.
Jeśli warunek nie zostaje spełniony, graf nie zawiera cyklu Eulera. Wtedy również wypisujemy komunikat.
Algorytm kończy swoje działanie.
Dla tak skonstruowanego algorytmu dane wejściowe opisujące graf reprezentujący Królewiec współcześnie wyglądałyby następująco:
Zaimplementuj w wybranym języku programowania omówiony algorytm sprawdzający, czy w danym grafie znajduje się cykl Eulera.
Poniżej znajduje się pseudokod innej funkcji sprawdzającej, czy dany graf jest grafem eulerowskim. Tym razem korzystamy jednak z listy sąsiedztwa, a nie macierzy sąsiedztwa jak wcześniej.
Argumentami funkcji są lista sąsiedztwa reprezentująca graf, na podstawie której sprawdzona zostanie parzystość stopni wierzchołków, oraz liczba wierzchołków grafu. Funkcja zwróci prawdziwy wynik jedynie w przypadku, gdy wejściowy graf jest spójny.
Specyfikacja problemu:
Dane:
listaSasiedztwa– lista sąsiedztwa grafu; tablica tablic (lista list) łańcuchów znakówliczbaWierzcholkow– liczba wierzchołków w grafie; liczba naturalna
Wynik:
komunikat informujący o tym, czy graf zawiera cykl Eulera
tak skonstruowanego algorytmu dane wejściowe opisujące graf reprezentujący Królewiec współcześnie wyglądałyby następująco:
Zaimplementuj w wybranym języku programowania omówiony algorytm sprawdzający, czy w danym grafie znajduje się cykl Eulera.
Ogólniejszy algorytm decydujący o istnieniu cyklu Eulera w grafie powinien również sprawdzać spójność grafu wejściowego. Jeden ze sposobów badania spójności grafu z użyciem algorytmu DFS (czyli przeszukiwania grafu w głąb) został omówiony w e‑materiałach:
Stopień grafu, stopień wierzchołka, grafy spójne – implementacja w języku C++Stopień grafu, stopień wierzchołka, grafy spójne – implementacja w języku C++,
Stopień grafu, stopień wierzchołka, grafy spójne – implementacja w języku JavaStopień grafu, stopień wierzchołka, grafy spójne – implementacja w języku Java,
Stopień grafu, stopień wierzchołka, grafy spójne – implementacja w języku PythonStopień grafu, stopień wierzchołka, grafy spójne – implementacja w języku Python.
Algorytm sprawdzający, czy graf zawiera ścieżkę Eulera – pseudokod
Przeanalizujmy teraz algorytm sprawdzający, czy w grafie można wyznaczyć ścieżkę Eulera. Nazywamy w ten sposób ścieżkęścieżkę, która przechodzi przez każdą krawędź grafu dokładnie raz i która nie musi kończyć się w wierzchołku, w którym się zaczynała.
Graf, który nie zawiera cyklu Eulera, a jedynie ścieżkę Eulera, nazywamy grafem półeulerowskim. Aby graf można było nazwać półeulerowskim, musi on spełniać warunek zawarty w poniższym twierdzeniu.
Graf spójny nazywamy grafem półeulerowskim wtedy i tylko wtedy, gdy zawiera on dokładnie dwa wierzchołki stopnia nieparzystego.
Na tej podstawie wcześniej przedstawiony algorytm można zmodyfikować tak, aby sprawdzał zarówno, czy graf jest eulerowski, jak i półeulerowski.
Specyfikacja problemu:
Dane:
macierzSasiedztwa– macierz sąsiedztwa grafu; tablica tablic (lista list) liczb naturalnych z przedziału <0, 1>
Wynik:
komunikat informujący o tym, czy graf jest eulerowski, półeulerowski lub nie jest ani eulerowski, ani półeulerowski
Zaczynamy od zapisania nagłówka funkcji istnienieSciezkiEulera, która jako argument przyjmuje macierz sąsiedztwa macierzSasiedztwa. W kolejnym kroku inicjalizujemy zmienną liczbaWierzcholkow jako rozmiar macierzy, czyli liczbę wierzchołków w grafie.
Następnie tworzymy tablicę (listę) stopnieWierzcholkow o długości liczbaWierzcholkow i wypełniamy ją wartościami początkowymi 0.
Zapisujemy pętlę, która będzie iterować po kolejnych wierzchołkach i zapisywać dla nich stopnie wierzchołków.
Wewnątrz tej pętli zapisujemy drugą pętlę, której zadaniem będzie sprawdzenie sąsiedztwa wierzchołka.
Dla każdego elementu tablicy (listy) stopnieWierzcholkow zwiększamy ten element o wartość zmiennej macierzSasiedztwa[i][j].
Po zakończeniu obu pętli obliczone zostają stopnie wszystkich wierzchołków.
Inicjalizujemy zmienną liczbaNieparzystych wartością 0. Zmienna będzie przechowywać liczbę wierzchołków o stopniu nieparzystym.
Uruchamiamy pętlę, aby zliczyć wierzchołki o stopniu nieparzystym.
Sprawdzamy warunek stopnieWierzcholkow[i] mod 2 != 0. Jeśli warunek jest spełniony, zwiększamy wartość zmiennej liczbaNieparzystych o 1.
Po zakończeniu pętli zostaje obliczona liczba wierzchołków o stopniu nieparzystym.
Wykonujemy instrukcję warunkową. Sprawdzamy, czy wartość zmiennej liczbaNieparzystych wynosi 0. Jeśli tak, oznacza to, że wszystkie wierzchołki mają stopień parzysty, a więc mamy do czynienia z grafem eulerowskim. Wypisujemy odpowiedni komunikat.
Jeśli wartość zmiennej liczbaNieparzystych wynosi 2, oznacza to, że dokładnie dwa wierzchołki mają stopień nieparzysty, co oznacza, że graf zawiera ścieżkę Eulera i jest grafem półeulerowskim. Wypisujemy odpowiedni komunikat.
W przeciwnym razie, gdy żaden z powyższych warunków nie jest spełniony, graf nie zawiera ani cyklu Eulera, ani ścieżki Eulera, zatem graf nie jest ani eulerowski, ani półeulerowski. Wypisujemy odpowiedni komunikat
Algorytm kończy swoje działanie.
Przykładowe dane wejściowe odpowiadające obecnym mostom królewieckim wyglądałyby tak jak w poprzednim algorytmie:
Zaimplementuj w wybranym języku programowania omówiony algorytm wyszukiwania ścieżki Eulera w grafie.
Przeanalizujmy teraz algorytm sprawdzający, czy w grafie można wyznaczyć ścieżkę Eulera, ale wykorzystujący listę sąsiedztwa.
Specyfikacja problemu:
Dane:
listaSasiedztwa– lista sąsiedztwa grafu; tablica tablic (lista list) łańcuchów znakówliczbaWierzcholkow– liczba wierzchołków w grafie; liczba naturalna
Wynik:
komunikat informujący o tym, czy graf jest eulerowski, półeulerowski lub nie jest ani eulerowski, ani półeulerowski
Przykładowe dane wejściowe odpowiadające obecnym mostom królewieckim wyglądałyby tak jak w poprzednim algorytmie:
Zaimplementuj w wybranym języku programowania omówiony algorytm wyszukiwania ścieżki Eulera w grafie.
Wykorzystaliśmy funkcję długość(). Ma ona swoje odpowiedniki w językach programowania.
C++
Przykład:
Java
Przykład:
Python
Przykład:
Słownik
ścieżka zamknięta, która zaczyna się i kończy w tym samym wierzchołku
graf, w którym możliwe jest połączenie dwóch wierzchołków za pomocą kilku krawędzi lub w którym występują krawędzie łączące wierzchołek sam ze sobą
trasa łącząca kolejne wierzchołki grafu, w której wszystkie krawędzie są różne