Ciąg, w którym wyrazy są liczbami, nazywamy ciągiem liczbowym.

Ciągiem skończonym nazywamy funkcję określoną na zbiorze $\left\{1, 2, 3, ..., n\right\}$.

Rozważmy ciąg $\left(a_n\right)$, którego wyrazy są liczbami $k$–cyfrowymi równymi sumie $k$–tych potęg swoich cyfr.

Wyrazami tego ciągu są na przykład liczby:

$153=1^3+5^3+3^3$

$370=3^3+7^3+0^3$

$371=3^3+7^3+1^3$

$1634=1^4+6^4+3^4+4^4$

$9474=9^4+4^4+7^4+4^4$

$54748=5^5+4^5+7^5+4^5+8^5$

$9926315=9^7+9^7+2^7+6^7+3^7+1^7+5^7$

Liczby te zwane są liczbami narcystycznymi.

Okazuje się, że istnieją dokładnie cztery liczby $3$–narcystyczne, trzy liczby $4$–narcystyczne, trzy liczby $5$–narcystyczne.

Wyrazy ciągu $\left(a_n\right)$ spełniają warunek

${10}^{k-1}\le a_n\le k·9^k$.

Ponieważ ${10}^{k-1}>k·9^k$ dla $k\ge 61$, to stwierdzamy, że liczb narcystycznych jest skończona ilość.

Można udowodnić, że ciąg $\left(a_n\right)$, jest tylko $88$–wyrazowy.

Przykłady ciągów liczb pierwszych, których pierwszym wyrazem jest $3$.

$\left(3, 7, 11\right)$ – ciąg, w którym różnica między wyrazami jest równa $4$,

$\left(3, \mathrm{11,} 19\right)$ – ciąg, w którym różnica między wyrazami jest równa $8$,

$\left(\mathrm{3,} \mathrm{23,} 43\right)$ – ciąg, w którym różnica między wyrazami jest równa $20$.

Rozważmy ciąg liczb pierwszych, mniejszych od $100$, postaci $4k+1$.

Kilka początkowych wyrazów tego ciągu:

$5$, $13$, $17$, $29$, $37$, $41$, $73$, $89$

Każda z takich liczb jest sumą kwadratów dwóch liczb naturalnych.

$5=1^2+2^2$

$13=2^2+3^2$

$17=1^2+4^2$

$29=2^2+5^2$

$37=1^2+6^2$

$41=4^2+5^2$

$73=3^2+8^2$

$89=5^2+8^2$

Niech $a$ będzie okresem ułamka $\frac{1}{7}$.

$\frac{1}{7}=0,142857142857...=0,\left(142857\right)$

$a=142857$

Rozważmy sześciowyrazowy ciąg $\left(a_n\right)$ wielokrotności liczby $a$.

$a_1=142857·1=142857$

$a_2=142857·5=714285$

$a_3=142857·4=571428$

$a_4=142857·6=857142$

$a_5=142857·2=285714$

$a_6=142857·3=428571$

Każdy wyraz tego ciągu składa się z tych samych cyfr co liczba $a$. Cyfra $1$ w zapisie dziesiętnym kolejnych wyrazów ciągu jest kolejno cyfrą setek tysięcy, dziesiątek tysięcy, jedności tysięcy, itd.

Zaobserwujmy inną ciekawą własność wyrazów ciągu $\left(a_n\right)$.

Dodajemy odpowiednio pogrupowane  cyfry pierwszego wyrazu ciągu, mnożymy pierwszy wyraz przez $7$.

$1+4+2+8+5+7=27\Rightarrow 2+7=9$

$14+28+57=99$

$142+857=999$

$142857·7=999999$

Wyniki kolejnych działań, to liczby, w których każda cyfra jest równa $9$.

Ciąg $\left(a_n\right)$ określony jest wzorem ogólnym $a_n=3^n-1$.

Początkowe wyrazy ciągu:

$a_1=2$

$a_2=8$

$a_3=26$

$a_4=80$

Zauważmy, że każdy wyraz tego ciągu jest liczbą parzystą. Zatem tylko pierwszy wyraz ciągu jest liczbą pierwszą.

W przedziale $⟨1, 500⟩$ istnieje tylko dziesięć liczb naturalnych $n$ takich, że lustrzane odbicie liczby $a_n$ jest liczbą pierwszą. Są to liczby:

$1$, $6$, $27$, $43$, $53$, $61$, $64$, $174$, $216$, $268$

Na przykład:

$a_6=3^6-1=729-1=728$

Liczba lustrzana to $827$ – jest to liczba pierwsza.

Tylko jedna liczba $a_n$ jest potęgą liczby naturalnej, jest to liczba $3^2-1$.

Trójkąt Herona, to taki trójkąt, którego długości boków, obwód i pole wyrażają się liczbami całkowitymi.

Każdy trójkąt pitagorejski jest trójkątem Herona. Przykładem trójkąta Herona, który nie jest trójkątem prostokątnym, jest trójkąt o bokach $5$, $5$, $6$, którego pole jest równe $12$. Trójkąt ten bowiem powstał z dwóch trójkątów pitagorejskich o bokach długości $3$, $4$, $5$ i wspólnym boku długości $4$.

Przykłady trójwyrazowych ciągów, których wyrazy są długościami boków trójkąta Herona.

$\left(5, 4, 3\right)$ – obwód trójkąta $12$, pole trójkąta $6$,

$\left(5, 8, 5\right)$ – obwód trójkąta $18$, pole trójkąta $12$,

$\left(13, 12, 5\right)$ – obwód trójkąta $30$, pole trójkąta $30$,

$\left(13, 13, 10\right)$ – obwód trójkąta $36$, pole trójkąta $60$,

$\left(15, 14, 13\right)$ – obwód trójkąta $42$, pole trójkąta $84$.

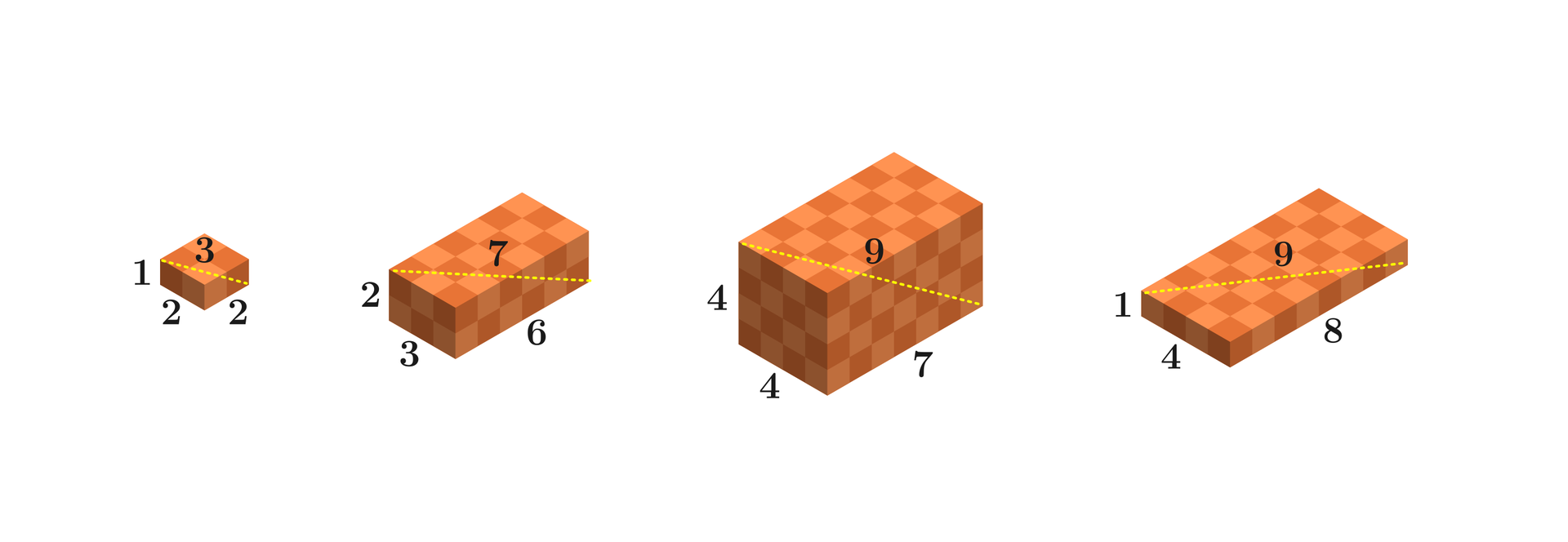
Ciąg czwórek pitagorejskich, to ciąg, którego wyrazami są takie liczby całkowite
$a$, $b$, $c$, $d$, że $a^2+b^2+c^2=d^2$.

Geometrycznie można zinterpretować liczby $a$, $b$, $c$, jako długości boków prostopadłościanu, którego przekątna ma długość $d$.

RSXu56auX5RBD

Ilustracja składa się z rysunków czterech prostopadłościanów. Pierwszy ma w podstawie kwadrat o boku 2, wysokość 1, a przekątna bryły ma długość trzy. Drugi prostopadłościan ma w podstawie prostokąt o bokach 3 i 6, wysokość 2, a przekątna bryły ma długość dwa. Trzeci prostopadłościan ma w podstawie prostokąt o bokach 4 i 7, wysokość 4, a przekątna bryły ma długość dziewięć. Czwarty prostopadłościan ma w podstawie prostokąt o bokach 4 i 8, wysokość 1, a przekątna bryły ma długość dziewięć.

Wzór opisujący czwórki pitagorejskie jest analogiczny do wzoru na stożek świetlny, którym posługują się fizycy. Przy okazji przypomnienie – stożek świetlny danego punktu czasoprzestrzeni, to zbiór punktów czasoprzestrzeni, których odległość czasoprzestrzenna od tego punktu wynosi zero.

Przykłady ciągów, których wyrazy są czwórkami pitagorejskimi.

$\left(\mathrm{2,} 3, \mathrm{6,} 7\right)$; $\left(\mathrm{4,} 4, \mathrm{7,} 9\right)$; $\left(\mathrm{6,} 6, \mathrm{7,} 11\right)$

$\left(2, \mathrm{10,} \mathrm{11,} 15\right)$; $\left(\mathrm{4,} \mathrm{13,} \mathrm{16,} 21\right)$; $\left(\mathrm{2,} \mathrm{10,} \mathrm{25,} 27\right)$

$\left(\mathrm{10,} \mathrm{10,} \mathrm{23,} 27\right)$; $\left(\mathrm{3,} \mathrm{16,} \mathrm{24,} 29\right)$; $\left(\mathrm{4,} 5, \mathrm{20,} 21\right)$

ciągiem skończonym nazywamy funkcję określoną na zbiorze $\left\{1, 2, 3, ..., n\right\}$