Graniastosłupem prawidłowym trójkątnym nazywamy graniastosłup prosty, którego podstawy są trójkątami równobocznymi.

Dany jest graniastosłup prostygraniastosłup prostygraniastosłup prosty czworokątny, którego podstawą jest romb o boku długości $4$ oraz kącie ostrym $60°$. Bryłę rozcięto wzdłuż krótszej przekątnej. Sprawdzimy, czy powstałe bryły to graniastosłupy prawidłowe trójkątne. Wyznaczymy sumę długości wszystkich krawędzi jednej z nowo powstałych brył wiedząc, że stosunek długości krawędzi podstawy do wysokości graniastosłupa wynosi $2:3$.

Rozwiązanie

Zaczniemy od wyznaczenia długości krószej przekątnej rombu.

R8URIWYIPydbO

Na ilustracji przedstawiono romb $ABCD$ o boku długości cztery. Kąty wewnętrzne przy przeciwległych wierzchołkach A i C mają miarę 60 stopni, natomiast katy wewnętrzne przy przeciwległych wierzchołkach B i D mają miarę 120 stopni. Zaznaczono krótszą przekątną rombu, łączącą wierzchołek B i D.

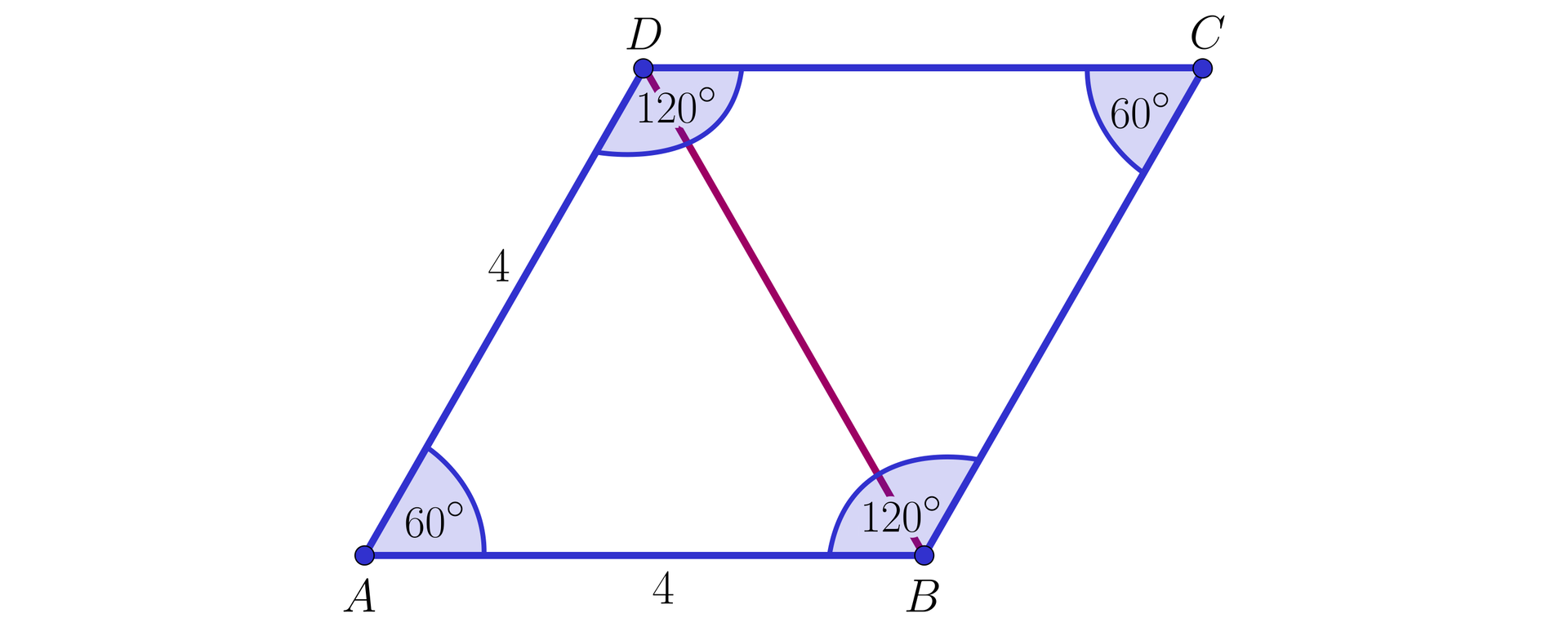
Zuważmy, że trójkąt $ABD$ jest równoboczny, ponieważ $\left|\measuredangle ABD\right|=\left|\measuredangle ADB\right|=60°$. Zatem $\left|BD\right|=4$.

Po rozcięciu bryły wzdłuż krótszej przekątnej rombu, podstawa podzieliła się na dwa trójkąty równoboczne, więc otrzymujemy w ten sposób dwa graniastosłupy prawidłowe trójkątne. Skoro stosunek długości krawędzi podstawy do wysokości bryły wynosi $2:3$, to

$\frac{a}{h}=\frac{2}{3}$, czyli $\frac{4}{h}=\frac{2}{3}$.

Wynika stąd, że $h=6$.

Suma krawędzi jednego graniastosłupa prawidłowego trójkątnego wynosi $3·6+6·4=18+24=42$.

Mamy dwa pudełka, w których znajdują się elementy budowy szkieletu graniastosłupa trójkątnego. W pierwszym pudełku są po dwa trójkąty równoboczne o bokach długości: $6 \text{cm}$, $3 \text{cm}$ oraz $2 \text{cm}$, natomiast w drugim pudełku są po trzy krawędzie boczne o długości: $4 \text{cm}$, $6 \text{cm}$, $14 \text{cm}$, $18 \text{cm}$, $20 \text{cm}$. Wyznaczymy na ile sposobów wybrane trójkąty z pierwszego pudełka oraz krawędzie z drugiego pudełka utworzą szkielet graniastosłupa prawidłowego trójkątnego.

Rozwiązanie

Aby utworzyć szkielet graniastosłupa prawidłowego trójkątnego muszą zachodzić jednocześnie dwa warunki:

• obydwa trójkąty równoboczne muszą mieć boki tej samej długości,

• trzy krawędzie boczne muszą mieć tę samą długość.

Zauważmy, że mamy $15$ możliwości spełniające warunki określone w treści zadania. Istotnie:

• jeżeli wybierzemy dwa trójkąty równoboczne o boku długości $6 \text{cm}$ to krawędzie mogą mieć długość $4 \text{cm}$, $6 \text{cm}$, $14 \text{cm}$, $18 \text{cm}$, $20 \text{cm}$,

• jeżeli wybierzemy dwa trójkąty równoboczne o boku długości $3 \text{cm}$ to krawędzie mogą mieć długość $4 \text{cm}$, $6 \text{cm}$, $14 \text{cm}$, $18 \text{cm}$, $20 \text{cm}$,

• jeżeli wybierzemy dwa trójkąty równoboczne o boku długości $2 \text{cm}$ to krawędzie mogą mieć długość $4 \text{cm}$, $6 \text{cm}$, $14 \text{cm}$, $18 \text{cm}$, $20 \text{cm}$.

Sprawdzimy, czy z drutu o długości $30$ można zbudować szkielet bryły będącej graniastosłupem prawidłowym trójkątnym, w którym długości krawędzi podstaw i długości krawędzi bocznych wyrażone są liczbą całkowitą dodatnią. Rozważymy wszystkie możliwości.

Rozwiązanie

Rozważmy graniastosłup prawidłowygraniastosłup prawidłowygraniastosłup prawidłowy trójkątny.

Niech $a\in {\mathrm{\mathbb{Z}}}_{+}$ oznacza długość krawędzi podstawy, a $b\in {\mathrm{\mathbb{Z}}}_{+}$ długość krawędzi bocznej rozważanego graniastosłupagraniastosłupgraniastosłupa.

Mamy $6$ krawędzi podstawy o długości $a$ oraz $3$ krawędzie boczne o długości $b$, zatem otrzymujemy równanie $6a+3b=30$, co daje: $2a+b=10$.

Zatem mamy następujące możliwości długości krawędzi graniastosłupa spełniające warunki zadania:

$\left\{\begin{array}{l}a=1\\ b=8\end{array}\right.$ lub $\left\{\begin{array}{l}a=2\\ b=6\end{array}\right.$ lub $\left\{\begin{array}{l}a=3\\ b=4\end{array}\right.$ lub $\left\{\begin{array}{l}a=4\\ b=2\end{array}\right.$

Mamy zatem cztery możliwe do zbudowania graniastosłupy prawidłowe trójkątne spełniające warunki zadania.

Graniastosłup prawidłowy sześciokątny rozcięto wzdłuż odcinków łączących środki co drugiej krawędzi podstawy. W wyniku rozcięcia otrzymano graniastosłup trójkątny.

RoYSuJFOV9DfK

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny, którego dolną podstawę oznaczono literami od A do F, natomiast górną odpowiednio literami z indeksem prim. Zaznaczono punkty stanowiące środki krawędzi podstaw. Punkt G na krawędzi $AB$, punkt H na krawędzi $CD$, punkt I na krawędzi $FI$ oraz w podstawie górnej punkty G prim, H prim, I prim. Zacieniowano trójkąty $GHI$ oraz $G\text{'}H\text{'}I\text{'}$.

a) Uzasadnimy, że jest to graniastosłup prawidłowy trójkątny.

b) Niech $a\in {ℝ}_{+}$ oznacza długość krawędzi podstawy graniastosłupa prawidłowego sześciokątnego. Obliczymy sumę długości wszystkich krawędzi podstaw nowo powstałego graniastosłupa trójkątnego.

Rozwiązanie

a) Zauważmy, że krawędzie podstawy nowo powstałego graniastosłupa trójkątnego stanowią dłuższą podstawę przystających trapezów równoramiennych $AGIF$, $GBCH$, $HDEI$, $A\text{'}G\text{'}I\text{'}F\text{'}$, $G\text{'}B\text{'}C\text{'}H\text{'}$, $H\text{'}D\text{'}E\text{'}I\text{'}$.

Zatem wszystkie te krawędzie podstaw są równe, więc podstawy są trójkątami równobocznymi

Stąd wynika, że nowo powstały graniastosłup jest graniastosłupem prawidłowym trójkątnym.

b) Rozpatrzmy jeden z takich trapezów równoramiennych $GIFA$.

RaJjUkLNd99bw

Na ilustracji przedstawiono trapez równoramienny, którego dolna podstawa jest dłuższa i oznaczona GI, natomiast górną oznaczono $AF$ i jej długość wynosi a. Długość ramion $AG$ oraz $FI$ wynosi $\frac{1}{2}a$. Z wierzchołka A opuszczono wysokość do podstawy, której spodek leży w punkcie K. Z wierzchołka F opuszczono wysokość do podstawy, której spodek leży w punkcie L. Odległość punktu K od G oraz L od I oznaczono x.

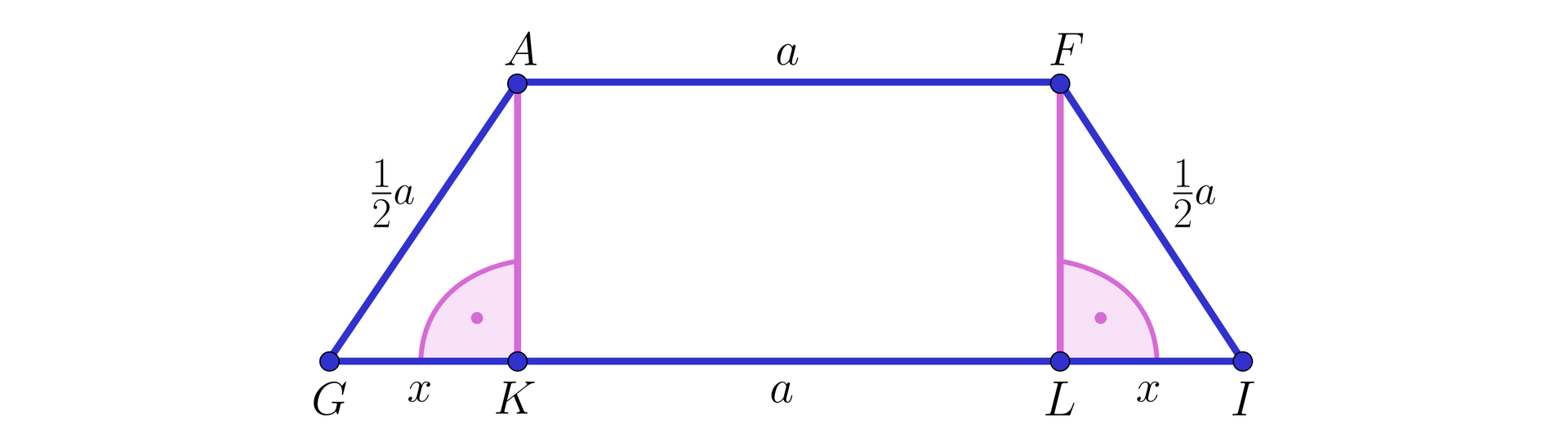
Zauważmy, że $\left|\sphericalangle GAF\right|=\left|\sphericalangle AFI\right|=120°$.

Oznaczymy: $\left|GK\right|=\left|LI\right|=x$ oraz $\left|AF\right|=\left|KL\right|=a$, stąd $\left|GA\right|=\left|FI\right|=\frac{1}{2}a$.

Z trójkąta $GKA$ mamy:

$\sin {30}^{\circ }=\frac{2x}{a}$.

Zatem: $\frac{2x}{a}=\frac{1}{2}$, co daje ostatecznie: $x=\frac{1}{4}a$.

Zatem długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego jest równa $a+2·\frac{1}{4}a=\frac{3}{2}a$, a suma długości wszystkich tych krawędzi wynosi $6·\frac{3}{2}a=9a$.

Graniastosłup prawidłowy sześciokątny rozcięto wzdłuż przekątnych podstaw przechodzących przez środki symetrii podstaw.

R1AWEGLYqbCMa

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny. Podstawę dolną sześciokąta oznaczono wielkimi literami alfabetu od A do F, natomiast górną literami od G do L. Zaznaczono 3 przekątne w podstawie górnej oraz dolnej. Środki przecięcia przekątnych podstawy dolnej i górnej połączono odcinkiem prostopadłym do płaszczyzny podstawy.

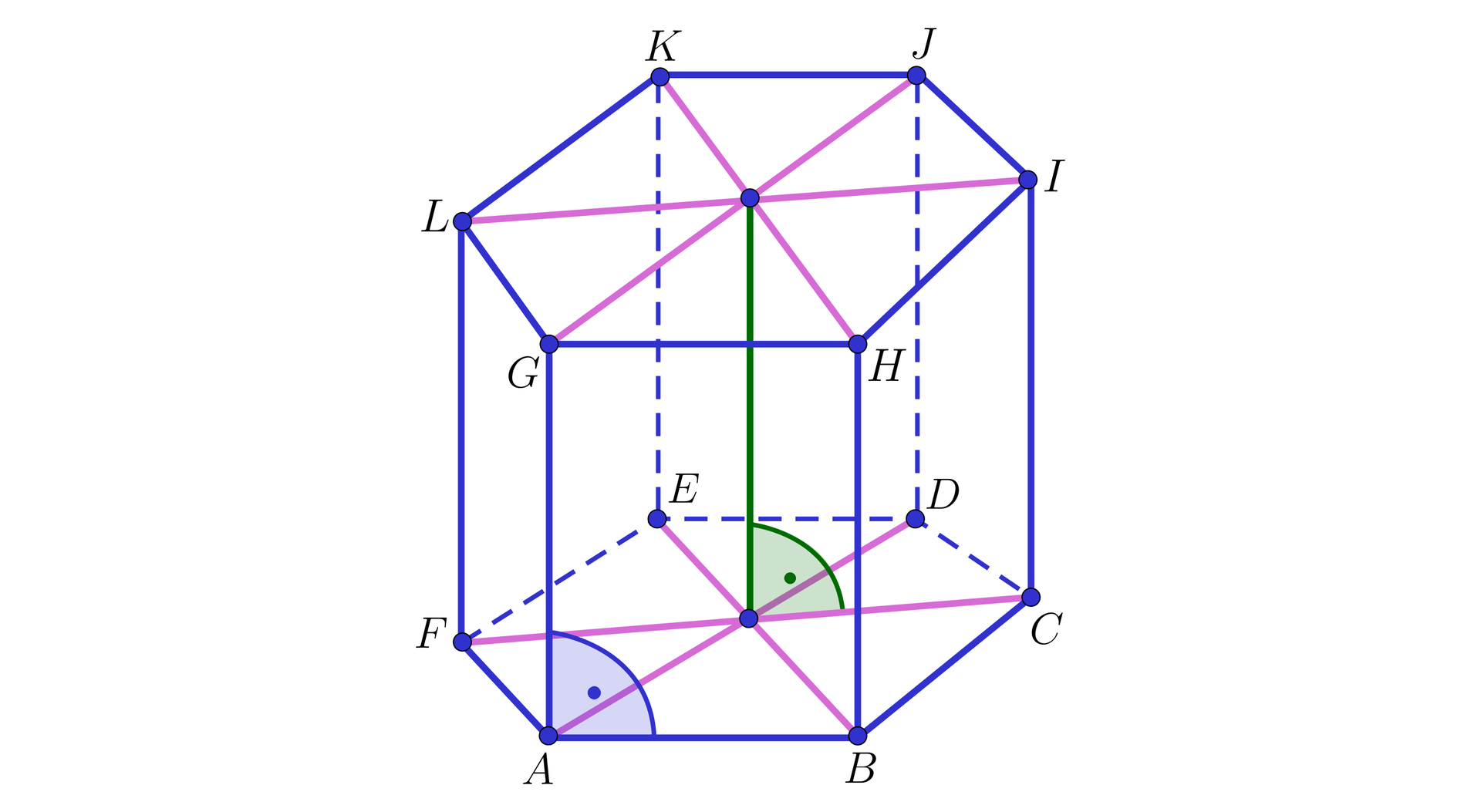
Następnie każdy z otrzymanych graniastosłupów prawidłowych trójkątnych pomalowano innym kolorem farby. Na ile sposobów, można “skleić” ze sobą dwa graniastosłupy prawidłowe trójkątne różnego koloru, aby otrzymać graniastosłup prosty czworokątny?

Rozwiązanie

1) W wyniku rozcięcia graniastosłupa prawidłowego sześciokątnego wzdłuż przekątnych przechodzących przez środki symetrii podstaw otrzymano $6$ graniastosłupów prawidłowych trójkątnych.

2) Oznaczmy kolory, jakimi pomalowano każdy z graniastosłupów prawidłowych trójkątnych, następująco $\left\{K_1, K_2, K_3, K_4, K_5, K_6\right\}$.

3) Zatem graniastosłupów prostych czworokątnych jest, tyle co dwuelementowych podzbiorów zbioru $\left\{K_1, K_2, K_3, K_4, K_5, K_6\right\}$.

4) Każdy taki podzbiór nazywamy dwuelementową kombinacją zbiorukombinacja zbiorukombinacją zbioru sześcioelementowego. Zatem $C_6^2=\frac{6!}{2!·4!}=15$.

wielościan, którego wszystkie wierzchołki leżą na dwóch płaszczyznach równoległych, zwanych płaszczyznami podstaw, dolnej i górnej, a którego wszystkie krawędzie nie leżące na tych płaszczyznach, zwane krawędziami bocznymi, są równoległe

graniastosłup, którego krawędzie boczne są prostopadłe do postaw

graniastosłup prosty, w którym podstawy są wielokątami foremnymi

każdy $k$-elementowy podzbiór zbioru $n$−elementowego $A$, gdzie $0⩽k⩽n$, nazywamy $k$−elementową kombinacją zbioru $A$; jeżeli $k⩽n$, to wszystkich $k$−elementowych kombinacji zbioru $n$−elementowego jest: $\frac{n!}{k!·\left(n-k\right)!}$