Układem równań liniowych z dwiema niewiadomymi nazywamy koniunkcję dwóch równań pierwszego stopnia z dwiema niewiadomymi.

Układ taki przyjmuje postać:

gdzie:
$x$ oraz $y$ – oznaczają niewiadome,
$a_1$, $a_2$, $b_1$ oraz $b_2$ – współczynniki przy niewiadomych odpowiednio $x$ oraz $y$, przy czym przynajmniej jedna z pary liczb $a_1$ i $a_2$ oraz $b_1$ i $b_2$ jest różna od zera,
$c_1$ i $c_1$ – nazywamy wyrazami wolnymi.

Rozwiązaniem układu równań liniowych z dwiema niewiadomymi jest każda  para liczb spełniających jednocześnie wszystkie równania danego układu równań.

Przy czym taki układ może mieć jedno rozwiązanie, nieskończenie wiele rozwiązań lub nie mieć rozwiązania.

Układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest dokładnie jedna para liczb, nazywamy układem oznaczonym.

W prostokątnym układzie współrzędnych narysujemy wykresy równań $x+y=5$ oraz $x-y=1$.

Przekształcimy każde z równań do postaci kierunkowej i znajdziemy po dwa rozwiązania każdego z nich.

$x+y=5$ i $x-y=1$

$y=-x+5$ i $-y=-x+1 \left|·\left(-1\right)\right.$

$y=-x+5$ i $y=x-1$

Wybieramy dowolny $x\in \mathrm{ℝ}$ i korzystając z równania obliczamy $y$.

$x=0\Rightarrow y=5$ i $x=0\Rightarrow y=-1$

$x=1\Rightarrow y=4$ i $x=1\Rightarrow y=0$

Otrzymujemy więc punkty należące odpowiednio do pierwszego oraz drugiego wykresu.

$\left(\mathrm{0,} 5\right)$, $\left(\mathrm{1,} 4\right)$ i $\left(0, -1\right)$, $\left(\mathrm{1,} 0\right)$

Zaznaczmy punktu w układzie współrzędnych, a następnie rysujemy wykresy tych równań.

R1OUd7aAwwuCh

Ilustracja przedstawia układ współrzędnych od 0 pięć do pięć. Zaznaczono wykres funkcji $x+y=5$ oraz $x-y=1$. Pierwsza funkcja ma miejsce zerowe w punkcie 5, a przecina oś y w punkcie pięć, a druga funkcja ma miejsce zerowe w punkcie jeden i przecina oś y w punkcie - jeden.

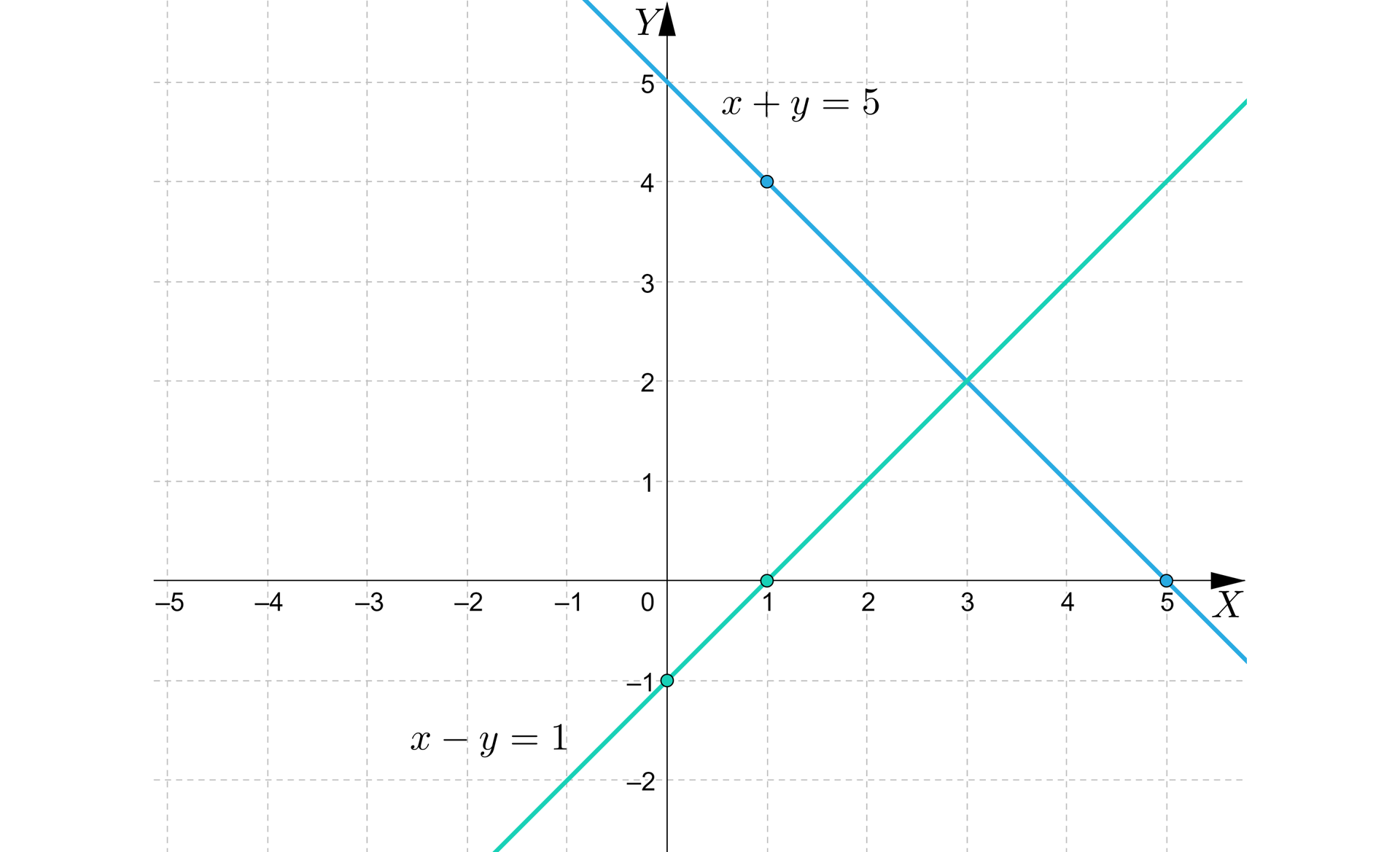
Otrzymany rysunek przedstawia interpretację geometryczną oznaczonego układu równań liniowych z dwiema niewiadomymiukład równań liniowych z dwiema niewiadomymiukładu równań liniowych z dwiema niewiadomymi. Wykresy równań składowych, to proste przecinające się w jednym punkcie. Współrzędne tego punktu spełniają pierwsze i drugie równanie. Spełniają więc układ równań, tworząc parę będącą rozwiązaniem układu równań.

RNOaf0ymUybhd

Ilustracja przedstawia układ współrzędnych od minus 5 do pięć. Zaznaczono wykres funkcji $x+y=5$ oraz $x-y=1$. Pierwsza funkcja ma miejsce zerowe w punkcie 5, a przecina oś y w punkcie pięć, a druga funkcja ma miejsce zerowe w punkcie jeden i przecina oś y w punkcie - jeden. Funkcja przecina się w pierwszej ćwiartce w punkcie trzy i dwa.

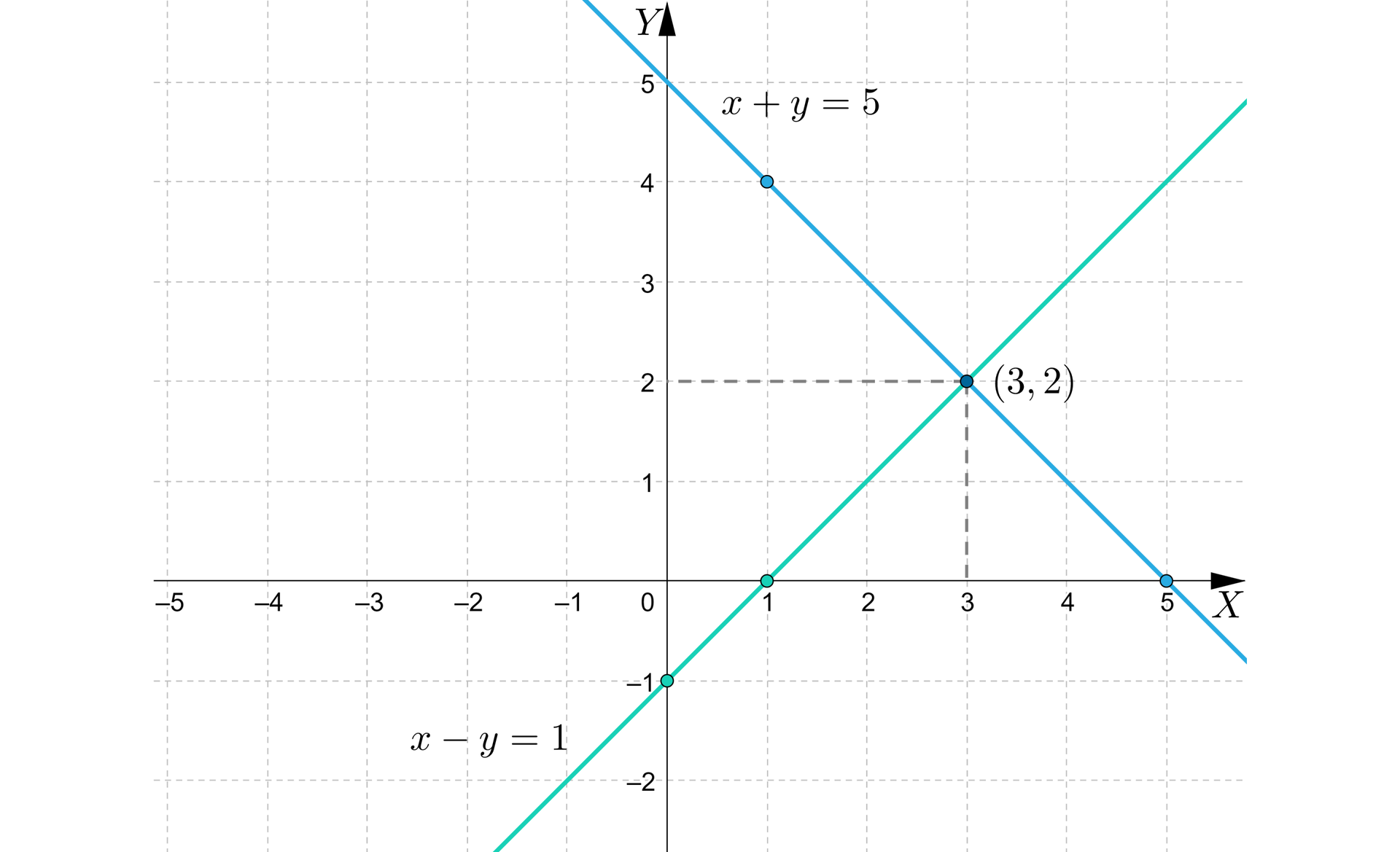
Na podstawie interpretacji geometrycznej możemy więc odczytać, że rozwiązaniem oznaczonego układu równańukład równań oznaczonyoznaczonego układu równań $\{\begin{array}{l}x+y=5\\ x-y=1\end{array}$ jest para liczb $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$.

Przedstawimy w prostokątnym układzie współrzędnych geometryczną interpretację układu równań $\left\{\begin{array}{l}2x-3y=9\\ -x+2y=-5\end{array}\right.$ i odczytamy z niej rozwiązanie tego układu.

$2x-3y=9$ i $-x+2y=-5$

$-3y=-2x+9 \left|:\left(-3\right)\right.$ i $2y=x-5 \left|:2\right.$

$y=\frac{2}{3}x-3$ i $y=\frac{1}{2}x-\frac{5}{2}$

$y=\frac{2}{3}x-3$ i $y=\frac{1}{2}x-2\frac{1}{2}$

Wyznaczamy po dwa punkty należące do wykresów równań.

$\left(0, -3\right)$, $\left(3, -1\right)$ i $\left(-1, -3\right)$, $\left(1, -2\right)$

Rysujemy wykresy równań składowych.

RkyeOCD2p3xZU

Ilustracja przedstawia układ współrzędnych od minus pięć do pięć. Zaznaczono na nim dwa wykresy funkcji liniowej. Pierwsza o wzorze $y=\frac{1}{2}x-2\frac{1}{2}$ zaznaczono na niej punkty minus jeden i minus trzy oraz jeden i minus dwa. Druga funkcja ma wzór $y=\frac{2}{3}x-3$ i przecina oś y w punkcie minus trzy. Wykresy dwóch funkcji przecinają się w czwartej ćwiartce w punkcie trzy i minus jeden.

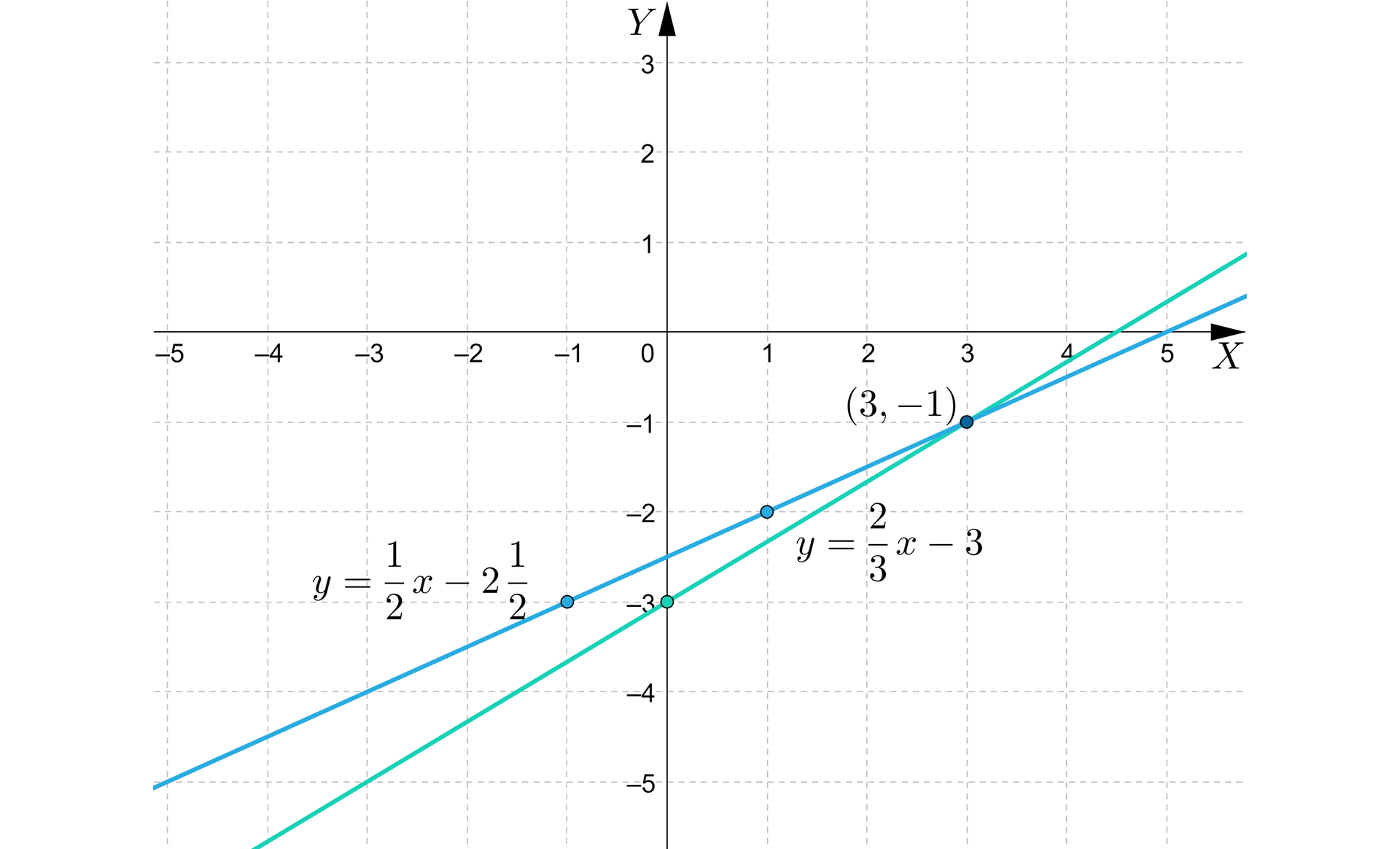
Wykresy przecinają się w punkcie o współrzędnych $\left(3, -1\right)$. Żeby mieć pewność, że liczby te są rozwiązaniem układu równańrozwiązanie układu równań liniowych z dwiema niewiadomymirozwiązaniem układu równań, wykonujemy sprawdzenie.

$L_1=2x-3y=2·3-3·\left(-1\right)=9=P_1$

$L_2=-x+2y=-3+2·\left(-1\right)=-5=P_2$

W obu równaniach otrzymaliśmy tożsamości, a zatem para liczb $\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right.$ jest rozwiązaniem tego układu równań.

Taki sposób rozwiązywania układów równań jest nazywany graficzną metodą rozwiązywania układów równań liniowych.

Rozwiążemy metodą graficzną układ równań

$\left\{\begin{array}{l}\frac{3·\left(x+y\right)}{2}-2·\left(y-x\right)=15 \\ {\left(x+3\right)}^2-2·{\left(y-1\right)}^2=23+x^2-2y^2\end{array}\right.$.

Przekształcamy każde z równań do postaci kierunkowej i znajdziemy po dwa rozwiązania każdego z nich.

$\frac{3·\left(x+y\right)}{2}-2·\left(y-x\right)=15 \left|·2\right.$ i ${\left(x+3\right)}^2-2·{\left(y-1\right)}^2=23+x^2-2y^2$

$3·\left(x+y\right)-4·\left(y-x\right)=30$ i $x^2+6x+9-2·\left(y^2-2y+1\right)=23+x^2-2y^2$

$3x+3y-4y+4x=30$ i $x^2+6x+9-2y^2+4y-2=23+x^2-2y^2$

$-y+7x=30$ i $6x+4y=23+2-9$

$-y=-7x+30$ i $4y=-6x+16 \left|:4\right.$

$y=7x-30$ i $y=-1,5x+4$

Wybieramy punkty, których współrzędne spełniają otrzymane równania.

$\left(4, -2\right)$, $\left(\mathrm{5,} 5\right)$ i $\left(\mathrm{0,} 4\right)$, $\left(\mathrm{2,} 1\right)$

RvqDT3xQ5uNia

Ilustracja przedstawia układ współrzędnych od minus 3 do sześciu. Pojawiają się dwa wykresy funkcji liniowych. Pierwszy o wzorze $y=-1,5x+4$, przecinający oś y w punkcie cztery. A drugi o wzorze $y=7x-30$, z zaznaczonym punktem pięć i pięć w pierwszej ćwiartce. Wykresy funkcji przecinają się w czwartej ćwiartce w punkcie cztery i minus dwa.

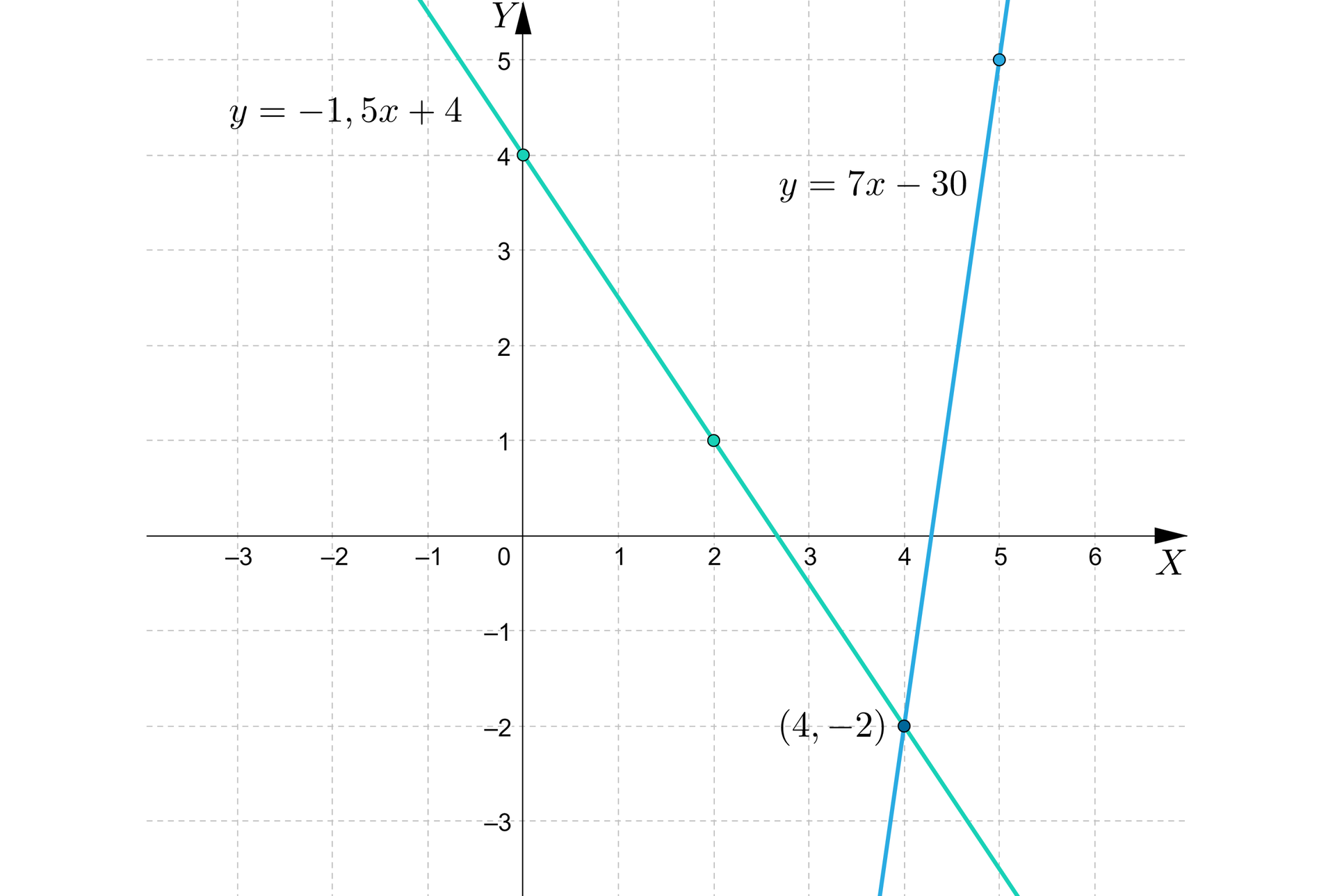
Wykresy przecinają się w punkcie o współrzędnych $\left(4, -2\right)$.

Sprawdzimy, czy prawidłowo odczytaliśmy rozwiązanie.

$L_1=\frac{3·\left(x+y\right)}{2}-2·\left(y-x\right)=\frac{3·\left(4-2\right)}{2}-2·\left(-2-4\right)=3+12=15=P_1$

$L_2={\left(x+3\right)}^2-2\cdot {\left(y-1\right)}^2={\left(4+3\right)}^2-2\cdot {\left(-2-1\right)}^2=49-18=31$

$P_2=23+x^2-2y^2=23+4^2-2·{\left(-2\right)}^2=23+16-8=31=L_2$

$L_1=P_1$ i $L_2=P_2$, a zatem para liczb $\left\{\begin{array}{l}x=4\\ y=-2\end{array}\right.$ jest rozwiązaniem tego układu równań.

Nie zawsze możemy łatwo  odczytać rozwiązanie na podstawie interpretacji geometrycznej.

Przedstawimy w prostokątnym układzie współrzędnych geometryczną interpretację układu równań $\left\{\begin{array}{l}5x+2y=3 \\ 4x-2y=-4\end{array}\right.$.

Przekształcamy każde z równań do postaci kierunkowej i znajdziemy po dwa rozwiązania każdego z nich.

$5x+2y=3$ i $4x-2y=-4$

$2y=-5x+3 \left|:2\right.$ i $-2y=-4x-4 \left|:\left(-2\right)\right.$

$y=-2,5x+1,5$ i $y=2x+2$

Wybieramy punkty.

$\left(-\mathrm{1,} 4\right)$, $\left(1, -1\right)$ i $\left(-\mathrm{1,} 0\right)$, $\left(\mathrm{1,} 4\right)$

RvrzlzrJgUVzb

Ilustracja przedstawia układ współrzędnych od minus pięciu do pięciu. Narysowano na nim dwa wykresy funkcji liniowej. Pierwsza o wzorze $y=-2,5x + 1,5$ z zaznaczonymi punktami minus jeden i cztery oraz jeden i minus jeden. Druga o wzorze $y=2x+2$ z miejscem zerowym wynoszącym minus jeden.

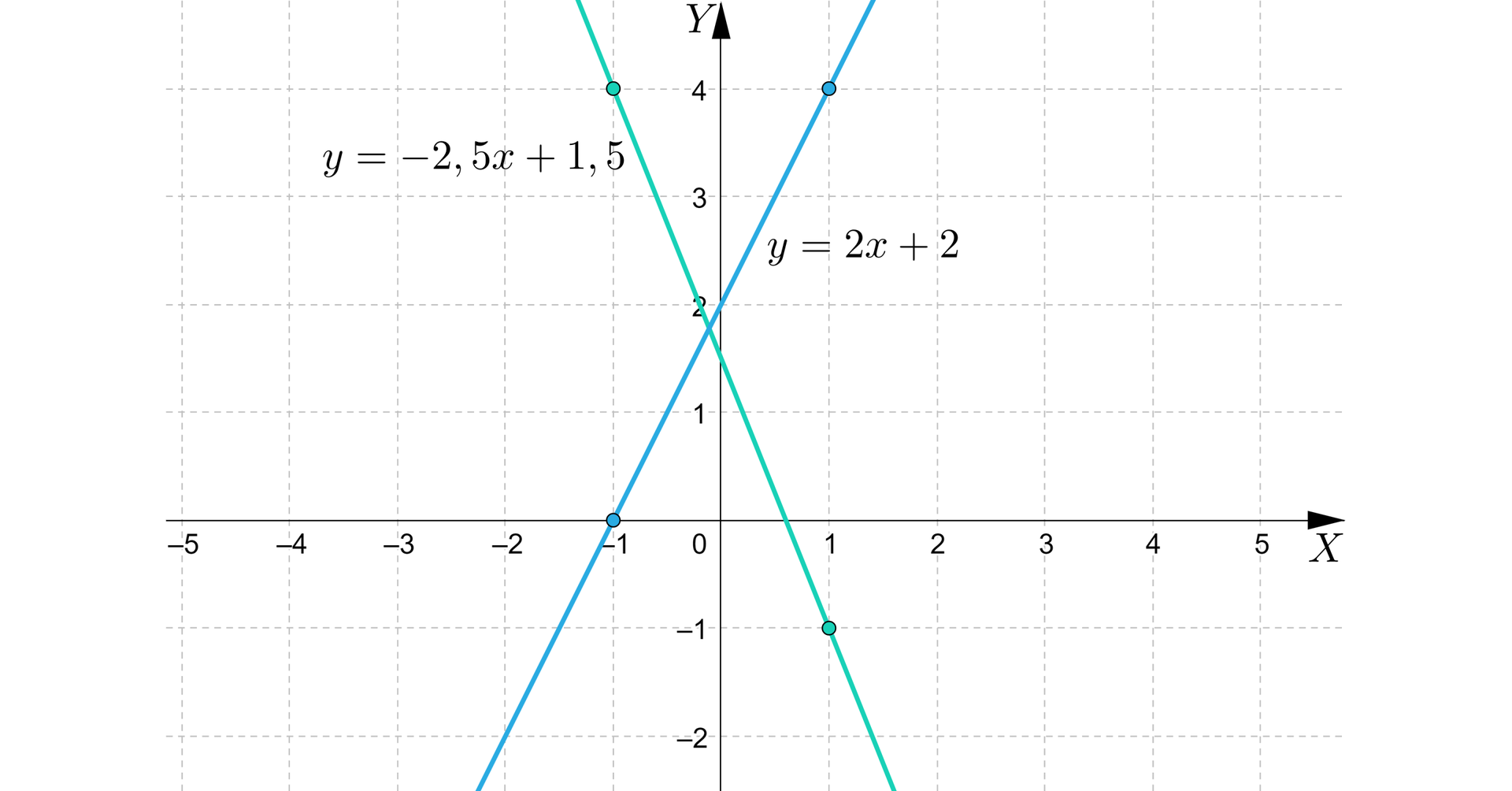
Graficzna metoda rozwiązywania układów równań wymaga dużej precyzji rysunku. A i tak nie zawsze jesteśmy w stanie odczytać rozwiązanie.

Rozwiązaniem tego układu równań jest para liczb $\left(-\frac{1}{9}, 1\frac{7}{9}\right)$ (sprawdź).

Aby znaleźć rozwiązanie należy skorzystać z jednej z metod algebraicznych, omówionych w innych materiałach.

Na rysunku przedstawiono interpretację geometryczną oznaczonego układu równańinterpretacja geometryczna oznaczonego układu równańinterpretację geometryczną oznaczonego układu równań liniowych z dwiema niewiadomymi. Zapiszemy ten układ równań.

R9rHAkrDnN5Cv

Ilustracja przedstawia układ współrzędnych od minus osiem do dwóch. Zaznaczono na nim dwa wykresy funkcji liniowej. Jedna o wzorze $y=a_{1}x+b_1$ mająca przecięcie z osią y w punkcie 4. Druga o wzorze $y=a_{2}x+b_2$ mająca przecięcie z osią y w punkcie minus trzy. Funkcje przecinają się w trzeciej ćwiartce w punkcie minus dwa i minus jeden.

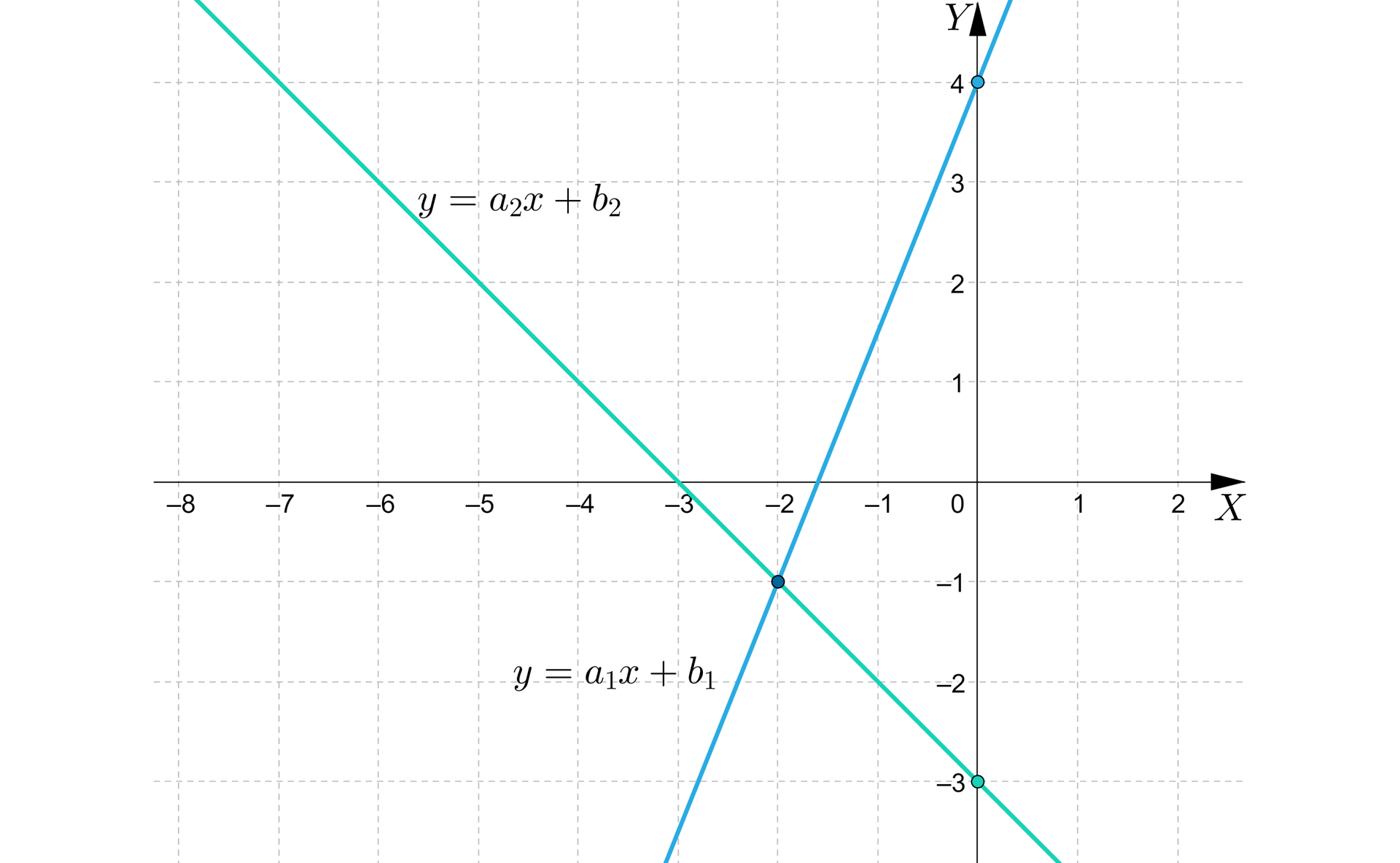
Na rysunku przedstawione są dwie proste, które są wykresami funkcji liniowych. Możemy więc opisać każdą z nich za pomocą wzoru $y=ax+b$.

Obie proste pochodzą przez punkt $\left(-2, -1\right)$.

Prosta $y=a_{1}x+b_1$ przecina oś $Y$ w punkcie $\left(\mathrm{0,} 4\right)$, a zatem, na podstawie własności funkcji liniowej wiemy, że $b_1=4$. Punkt $\left(-2, -1\right)$ należy do prostej, więc jego współrzędne spełnią jej równanie. Mamy zatem:

$a_1·\left(-2\right)+4=-1$

$-2a_1=-5 | :\left(-2\right)$

$a_1=2,5$

A zatem równanie tej prostej ma postać $y=2,5x+4$.

Prosta $y=a_{2}x+b_2$ przecinana oś $Y$ w punkcie $\left(0, -3\right)$, a zatem, na podstawie własności funkcji liniowej wiemy, że $b_2=-3$. Punkt $\left(-2, -1\right)$ należy do prostej, więc jego współrzędne spełnią jej równanie. Mamy zatem:

$a_2·\left(-2\right)-3=-1$

$a_2=-1$

A zatem równanie tej prostej ma postać $y=-x-3$.

Wykresy przedstawione na rysunku są więc ilustracją geometryczną układu równań liniowych $\left\{\begin{array}{l}y=2,5x+4\\ y=-x-3\end{array}\right.$.

Obliczymy pole trójkąta, którego wierzchołki znajdują się w punktach przecięcia prostych:

$k$ : $y-2=0$,
$l$ : $2x-y+8=0$,
$m$ : $x+y-5=0$.

Przekształcamy każde z równań do postaci kierunkowej i rysujemy ich wykresy.

$y-2=0$ i $2x-y+8=0$ oraz $x+y-5=0$

$y=2$ i $-y=-2x-8$ oraz $y=-x+5$

$y=2$ i $y=2x+8$ oraz $y=-x+5$

$\left(-\mathrm{1,} 2\right)$, $\left(\mathrm{1,} 2\right)$ i $\left(-\mathrm{2,} 4\right)$, $\left(\mathrm{0,} 8\right)$ oraz $\left(\mathrm{0,} 5\right)$, $\left(\mathrm{1,} 4\right)$

R16nRCVH9KO6n

Ilustracja przedstawia układ współrzędnych od minus cztery do pięciu. Zaznaczono na nim trzy wykresy funkcji liniowych. Pierwszy pionowy o wzorze $y=2$, drugi o wzorze $y=2x+8$ przecinający się z osią y w punkcie osiem, a trzeci wykres wyrażony wzorem $y=-x+5$ przecinający się z osią y w punkcie pięć.

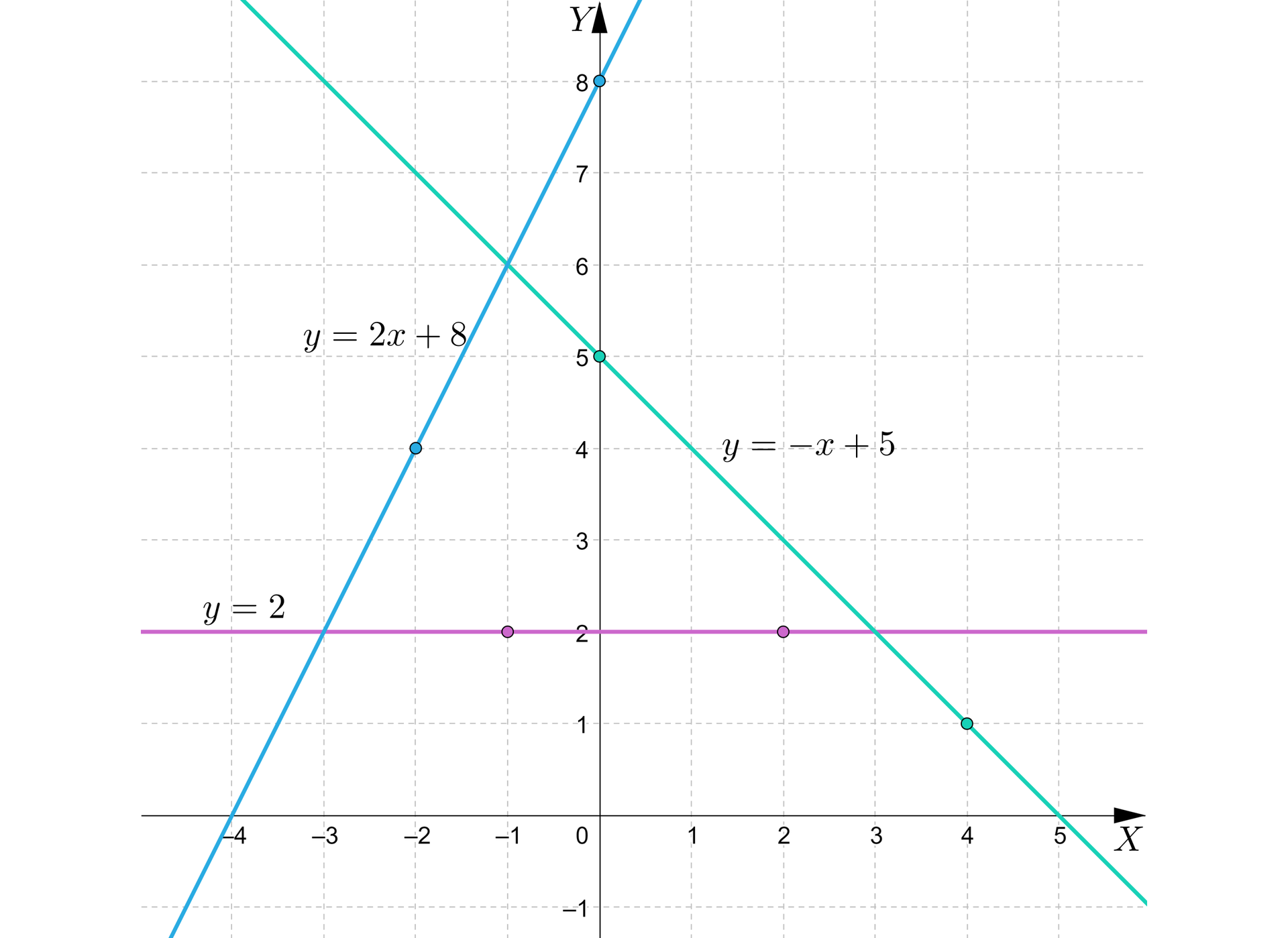
Wierzchołki figury – punkty przecięcia prostych, możemy wyznaczyć za pomocą odpowiednich układów równań.

Współrzędne punktu $B$, przecięcia się prostych $k$ oraz $m$, możemy wyznaczyć rozwiązując układ równań $\left\{\begin{array}{l}y=2\\ y=-x+5\end{array}\right.$.

Współrzędne punktu $A$, przecięcia się prostych $k$ oraz $l$, możemy wyznaczyć rozwiązując układ równań $\left\{\begin{array}{l}y=2\\ y=2x+8\end{array}\right.$.

Współrzędne punktu $C$, przecięcia się prostych $l$ oraz $m$, możemy wyznaczyć rozwiązując układ równań $\left\{\begin{array}{l}y=2x+8\\ y=-x+5\end{array}\right.$.

RVCN07WKWKrBQ

Ilustracja przedstawia układ współrzędnych od minus cztery do pięciu. Zaznaczono na nim trzy wykresy funkcji liniowych. Pierwszy pionowy o wzorze $y=2$, drugi o wzorze $y=2x+8$ przecinający się z osią y w punkcie osiem, a trzeci wykres wyrażony wzorem $y=-x+5$ przecinający się z osią y w punkcie pięć. Wykresy te tworzą trójkąt A B C o wysokości równej 4 jednostki. Wysokość upuszczona jest na podstawę o długości a.

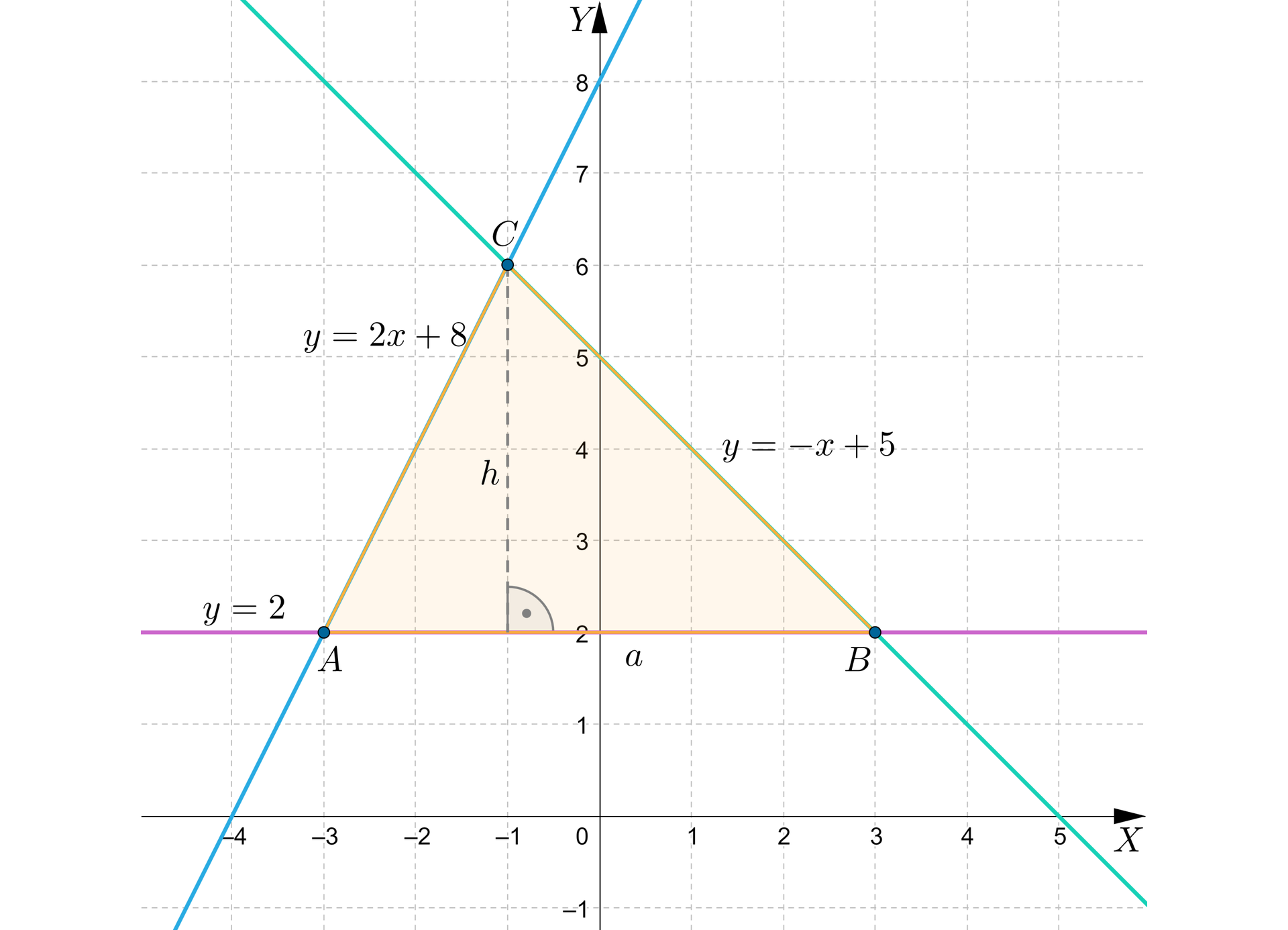
Odczytujemy z rysunku współrzędne wierzchołków:

$A=\left(-\mathrm{3,} 2\right)$,

$B=\left(\mathrm{3,} 2\right)$,

$C=\left(-\mathrm{1,} 6\right)$.

Odczytujemy długości odcinków $a=6\left[\mathrm{j}\right]$ oraz $h=4 \left[\mathrm{j}\right]$.

Obliczmy pole trójkąta podstawiając odczytane dane do wzoru:

$P=\frac{a·h}{2}=\frac{6·4}{2}=12$

Pole trójkąta $ABC$ jest równe $12 \left[{\mathrm{j}}^2\right]$.

układ równań postaci

każda para liczb spełniających każde z równań składowych w tym układzie

układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest dokładnie jedna para liczb

dwie proste przecinające się w punkcie, którego współrzędne tworzą parę liczb, bedącą  rozwiązaniem układu równań