Przeczytaj

Przypomnijmy definicję funkcji kwadratowej.

Funkcja kwadratowa

Definicja: Funkcja kwadratowa

Funkcję określoną na zbiorze $ℝ$ wzorem

f (x) = a x^{2} + b x + c

gdzie:
$a$ , $b$ , $c \in ℝ$ oraz $a \neq 0$

nazywamy funkcją kwadratową.

Funkcja kwadratowa ma wiele ciekawych własności, które mają zastosowanie w rozwiązywaniu problemów praktycznych.

W przedstawionych przykładach wykorzystamy niektóre własności funkcji kwadratowej:

istnienie wartości najmniejszej lub największej funkcji kwadratowej,

postać ogólną, kanoniczną, iloczynową wzoru funkcji kwadratowej,

miejsca zerowe oraz oś symetrii paraboli, która jest wykresem funkcji kwadratowej,

zastosowanie funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej w interpretowaniu zjawisk fizycznych.

Przykład 1

Zdjęcie oprawiono w ramę o zewnętrznych wymiarach $9 dm$ i $6 dm$ tak, że pole powierzchni widocznej części zdjęcia wynosi $18 {dm}^{2}$ . Obliczymy szerokość tej ramy.

Rozwiązanie:

Wykonujemy rysunek pomocniczy i wprowadźmy oznaczenia, jak na poniższym rysunku.

RHGLiLY851EvJ

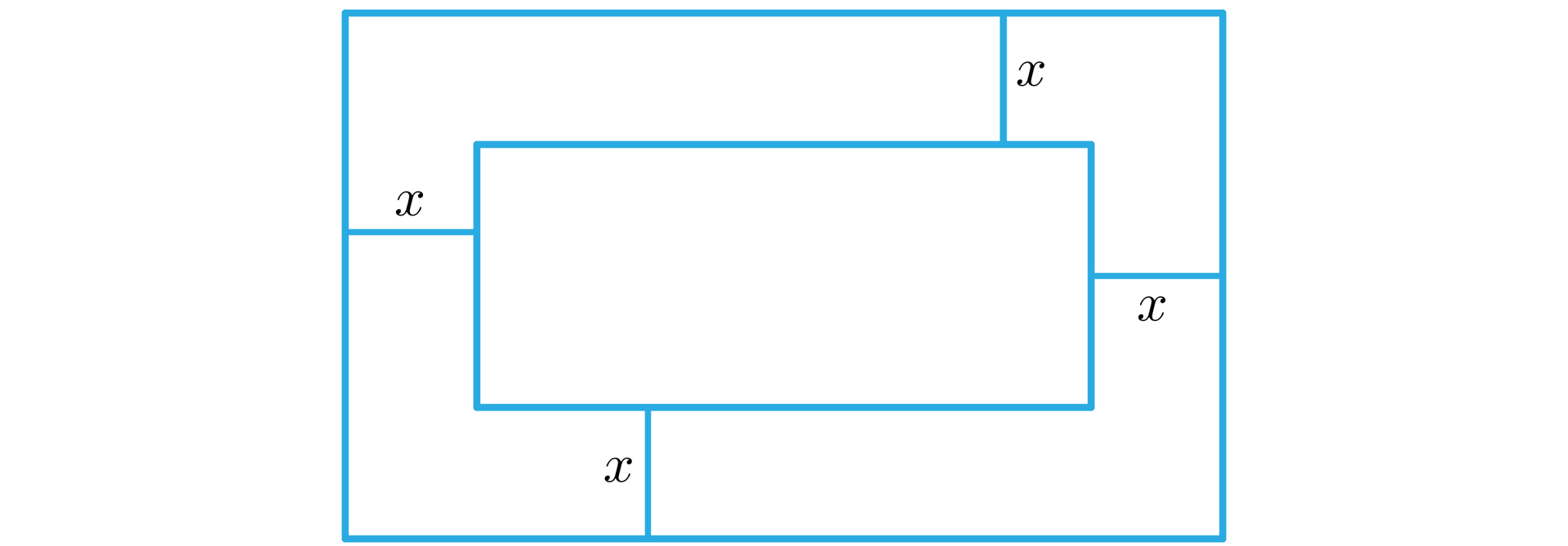
Jeżeli przez $x$ oznaczymy szerokość ramy w $d m$ , to $6 - x > 0$ oraz $9 - x > 0$ .

Zatem $x \in (0, 6)$ .

Do wyznaczenia wartości $x$ rozwiązujemy równanie:

$(9 - 2 x) \cdot (6 - 2 x) = 18$

$54 - 18 x - 12 x + 4 x^{2} - 18 = 0$

$2 x^{2} - 15 x + 18 = 0$

$∆ = 225 - 8 \cdot 18 = 81$

$x_{1} = \frac{15 - 9}{4} = \frac{6}{4} = \frac{3}{2}$

$x_{2} = \frac{15 + 9}{4} = \frac{24}{4} = 6$

Ponieważ $x \in (0, 6)$ , zatem rama ma szerokość $\frac{3}{2} dm$ .

Przykład 2

Drogę w ruchu jednostajnie przyspieszonym opisuje wzór $s = v_{0} \cdot t + \frac{a \cdot t^{2}}{2}$ , gdzie $v_{0}$ - prędkość poczatkowa ciała w $\frac{m}{s}$ , $a$ - przyspieszenie w $\frac{m}{s^{2}}$ , $s$ - długość przebytej drogi w $m$ , $t$ - czas trwania ruchu w $s$ . Wyznaczymy z tego wzoru czas trwania ruchu.

Rozwiązanie:

Do wyznaczenia czasu $t$ wykorzystamy podany wzór:

$s = v_{0} \cdot t + \frac{a \cdot t^{2}}{2}$

Wzór ten możemy przekształcić do następującej postaci:

$a t^{2} + 2 v_{0} t - 2 s = 0$

Wyznaczamy t:

$∆ = {(2 v_{0})}^{2} - 4 \cdot a \cdot (- 2 s) = 4 {v_{0}}^{2} + 8 a s$

$\sqrt{∆} = \sqrt{4 {v_{0}}^{2} + 8 a s} = 2 \sqrt{{v_{0}}^{2} + 2 a s}$

$t_{1} = \frac{- 2 v_{0} - 2 \sqrt{{v_{0}}^{2} + 2 a s}}{2} = - v_{0} - \sqrt{{v_{0}}^{2} + 2 a s} < 0$

$t_{2} = \frac{- 2 v_{0} + 2 \sqrt{{v_{0}}^{2} + 2 a s}}{2} = - v_{0} + \sqrt{{v_{0}}^{2} + 2 a s} > 0$

Zatem czas trwania ruchu ciała można wyznaczyć ze wzoru $t = - v_{0} + \sqrt{v_{0}^{2} + 2 a s}$ $[s]$ .

Przykład 3

Na rysunku przedstawiono schemat ulicznej latarni. Słup, podtrzymujący latarnię został zaprojektowany na kształt paraboli, będącej wykresem funkcji kwadratowej. Do latarni zamocowano pręt (w kolorze żółtym), jak na rysunku (bokowi jednej kratki odpowiada 1 m) .

R4rgkYzrZ05PU

Wyznaczymy długość pręta, który zamocowano do latarni.

Rozwiązanie:

Możemy przyjąć, że długość pręta jest równa odległości pomiędzy miejscami zerowymi pewnej funkcji kwadratowej, której wykres przedstawiono na rysunku.

Z paraboli, będącej wykresem funkcji kwadratowej odczytujemy współrzędne zaznaczonych punktów:

$(1, - 2)$ , $(2, \frac{3}{2})$ oraz $(5, 0)$ .

Jeżeli wykorzystamy postać ogólną wzoru funkcji kwadratowej $f (x) = a x^{2} + b x + c$ , to do wyznaczenia wartości $a$ , $b$ , $c$ rozwiązujemy układ równań:

$\{\begin{cases} - 2 = a \cdot 1^{2} + b \cdot 1 + c \\ \frac{3}{2} = a \cdot 2^{2} + b \cdot 2 + c \\ 0 = a \cdot 5^{2} + b \cdot 5 + c \end{cases}$

$\{\begin{cases} - 2 = a + b + c \\ 3 = 8 a + 4 b + 2 c \\ 0 = 25 a + 5 b + c \end{cases}$

Zatem $a = - 1$ , $b = \frac{13}{2}$ , $c = - \frac{15}{2}$ .

Jeżeli $p$ jest pierwszą współrzędną wierzchołka paraboli, która jest wykresem odpowiedniej funkcji kwadratowej oraz $x_{1}$ i $x_{2}$ są miejscami zerowymi funkcji kwadratowej, to:

$p = \frac{x_{1} + x_{2}}{2}$

Zatem do wyznaczenia wartości $x_{1}$ rozwiązujemy równanie:

$\frac{- \frac{13}{2}}{- 2} = \frac{x_{1} + 5}{2}$

$x_{1} = \frac{3}{2}$

Wobec tego szukana długość pręta wynosi:

$5 - \frac{3}{2} = 3, 5$ $[m]$

Przykład 4

Sklep sprzedaje dziennie $16$ zabawek. Zysk ze sprzedaży jednej sztuki wynosi $40 zł$ . Wiadomo, że obniżenie ceny o każde $5 zł$ , powoduje wzrost sprzedaży o $4$ sztuki dziennie. Obliczymy, ile powinna wynosić cena zabawki, aby zysk był największy.

Rozwiązanie:

Wprowadźmy następujące oznaczenia:

$x$ - liczba obniżek ceny zabawki,

$5 x$ - obniżka $x$ raz ceny zabawki za każdym razem o $5 z ł$

$4 x$ - wielkość opisująca wzrost liczby sprzedanych zabawek po $x$ obniżkach ceny zabawki

Niech funkcja $f$ wyraża dzienny zysk ze sprzedaży.

Zatem:

$f (x) = (40 - 5 x) \cdot (16 + 4 x)$ , gdzie $x \in ⟨ 0, 8 ⟩$

$f (x) = 640 + 160 x - 80 x - 20 x^{2} = - 20 x^{2} + 80 x + 640$

Wykres tej funkcji leży na paraboli o ramionach skierowanych do góry.

Zatem funkcja osiąga wartość największą w punkcie, który jest wierzchołkiem paraboli.

Wobec tego $p = \frac{- 80}{2 \cdot (- 20)} = 2$ .

Zatem należy dwukrotnie obniżyć cenę, aby zysk był największy.

Cena powinna wynosić:

$(40 - 5 \cdot 2) zł = 30 zł$

Przykład 5

Na wykresie przedstawiono zależność drogi od czasu w ruchu jednostajnie przyspieszonym prostoliniowym. Drogę w ruchu jednostajnie przyspieszonym prostoliniowym określamy wzorem $s (t) = \frac{a \cdot t^{2}}{2}$ , gdzie $s$ oznacza przebytą drogę w czasie $t$ , zaś $a$ – przyspieszenie. Zakładamy, że ciało przed rozpoczęciem ruchu znajdowało się w stanie spoczynku.

R1KSu0IdtPhU2

a) Na podstawie wykresu wyznaczymy wartość przyspieszenia $a$ .

b) Obliczymy długość drogi, jaką pokonało ciało w czasie $50 s$ .

Rozwiązanie:

a) Zauważmy, że do wykresu funkcji przedstawionego na rysunku należy punkt o współrzędnych $(1, 3)$ .

Zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$3 = \frac{a \cdot 1^{2}}{2}$

$a = 6 \frac{m}{s^{2}}$

b) Jeżeli $t = 50 s$ , to:

$s (50) = \frac{6 \cdot 50^{2}}{2} = 7500$

W ciągu $50 s$ ciało pokonało drogę długości $7500 m$ .

Przykład 6

Cena wynajmu autobusu na wycieczkę wynosi $1500 zł$ . Gdyby 5 uczestników zrezygnowało z wycieczki, to każdy z pozostałych zapłaciłby $10 zł$ więcej. Obliczymy, ilu uczestników zapisało się na wycieczkę.

Rozwiązanie:

Wprowadźmy następujące oznaczenia:

$x$ – liczba uczestników,

$y$ – koszt wynajmu autobusu na jednego uczestnika.

Do wyznaczenia wartości $x$ i $y$ rozwiązujemy układ równań:

$\{\begin{cases} x \cdot y = 1500 \\ (x - 5) \cdot (y + 10) = 1500 \end{cases}$

Zauważmy, że każde z równań możemy zapisać w postaci równania wymiernego.

$\{\begin{cases} y = \frac{1500}{x} \\ x y + 10 x - 5 y - 50 = 1500 \end{cases}$

$1500 + 10 x - 5 \cdot \frac{1500}{x} - 50 = 1500$

$10 x^{2} - 50 x - 7500 = 0$

$x^{2} - 5 x - 750 = 0$

$∆ = 25 + 4 \cdot 750 = 3025$

$x_{1} = \frac{5 - 55}{2} = - 25$

$x_{2} = \frac{5 + 55}{2} = 30$

Ponieważ $x > 0$ , zatem $x = 30$ .

Na wycieczkę zapisało się $30$ uczestników.

Słownik

funkcja kwadratowa

funkcja określona na zbiorze $ℝ$ wzorem

f (x) = a x^{2} + b x + c

gdzie:
$a$ , $b$ , $c \in ℝ$ oraz $a \neq 0$

Wprowadzenie

Infografika

Słownik