Przeczytaj

Układ równań drugiego stopnia z dwiema niewiadomymi

Definicja: Układ równań drugiego stopnia z dwiema niewiadomymi

Układ dwóch równań z dwiema niewiadomymi, z których przynajmniej jedno jest stopnia drugiego, nazywamy układem drugiego stopnia.

W szczególności układem równań drugiego stopnia jest układ składający się z równania liniowego oraz kwadratowego.

Przykład 1

Rozwiążmy układ równań drugiego stopnia z dwiema niewiadomymi:

a) $\{\begin{cases} y = x^{2} - 3 x + 8 \\ x + y = 11 \end{cases}$

Rozwiązanie:

Z drugiego równania wyznaczamy $y$ , ponieważ występuje w pierwszej potędze:

$\{\begin{cases} y = x^{2} - 3 x + 8 \\ y = 11 - x . \end{cases}$

Wyrażenie $11 - x$ wstawiamy w miejsce $y$ do pierwszego równania:

$\{\begin{cases} x^{2} - 3 x + 8 = 11 - x \\ y = 11 - x \end{cases}$

i porządkujemy pierwsze równanie skąd otrzymujemy:

$\{\begin{cases} x^{2} - 2 x - 3 = 0 \\ y = 11 - x . \end{cases}$

Otrzymaliśmy w ten sposób równanie kwadratowe z którego wyznaczymy rozwiązania o ile istnieją. Zaczynamy od wyznaczenia wyróżnika trójmianu kwadratowego:

$Δ = b^{2} - 4 a c = 4 + 12 = 16$ , $\sqrt{Δ} = 4$ .

Stąd wynika, że

$x_{1} = \frac{2 - 4}{2} = - 1$ oraz $x_{2} = \frac{2 + 4}{2} = 3$

Wyznaczając $y$ odpowiednio dla $x_{1}$ i $x_{2}$ dostajemy

$y_{1} = 11 - (- 1) = 12$ oraz $y_{2} = 11 - 3 = 8$ .

Odpowiedź:

Rozwiązaniem układu równań są pary liczb $\{\begin{cases} x = - 1 \\ y = 12 \end{cases}$ i $\{\begin{cases} x = 3 \\ y = 8 . \end{cases}$

b) $\{\begin{cases} y = x^{2} + 5 x - 3 \\ y = 3 x - 6 \end{cases}$

Rozwiązanie:

Z równania liniowego wyznaczamy niewiadomą $y$ .

Wyrażenie $3 x - 6$ wstawiamy w miejsce $y$ do pierwszego równania:

$\{\begin{cases} x^{2} + 5 x - 3 = 3 x - 6 \\ y = 3 x - 6 \end{cases}$

i porządkujemy pierwsze równanie skąd otrzymujemy:

$\{\begin{cases} x^{2} + 2 x + 3 = 0 \\ y = 3 x - 6 . \end{cases}$

Otrzymaliśmy w ten sposób równanie kwadratowe z którego wyznaczymy rozwiązania o ile istnieją. Zaczynamy od wyznaczenia wyróżnika trójmianu kwadratowego:

$Δ = b^{2} - 4 a c = 4 - 12 = - 8 < 0$ .

Wyróżnik trójmianu kwadratowego jest ujemny, zatem równanie nie posiada rozwiązań w zbiorze liczb rzeczywistych.

Odpowiedź:

Układ równań nie ma rozwiązań.

c) $\{\begin{cases} 4 x^{2} - y^{2} = 0 \\ 2 x - y = 0 \end{cases}$

Rozwiązanie:

Z drugiego równania układ wyznaczamy $y$

$\{\begin{cases} 4 x^{2} - y^{2} = 0 \\ y = 2 x . \end{cases}$

Wyrażenie $2 x$ wstawiamy w miejsce $y$ do pierwszego równania:

$\{\begin{cases} 4 x^{2} - 4 x^{2} = 0 \\ y = 2 x . \end{cases}$

porządkujemy pierwsze równanie i stąd otrzymujemy:

$\{\begin{cases} 0 = 0 \\ y = 2 x . \end{cases}$

Odpowiedź:

Układ równań ma nieskończenie wiele rozwiązań $\{\begin{cases} x \in ℝ \\ y = 2 x \end{cases}$ . Pary liczb, będące rozwiązaniami układu równań są współrzędnymi punktów, które leżą na prostej $y = 2 x$ .

Interpretacja geometryczna układów równań drugiego stopnia

Równanie liniowe $A x + B y + C = 0$ (jeśli współczynniki przy zmiennych nie są równocześnie równe $0$ ) jest równaniem prostej na płaszczyźnie, a równanie kwadratowe $y = a x^{2} + b x + c$ , $a \neq 0$ jest równaniem paraboli na płaszczyźnie. Zatem rozwiązanie układu równań, z których jedno jest liniowe, a drugie kwadratowe:

\{\begin{cases} A x + B y + C = 0 \\ a x^{2} + b x + c = 0 \end{cases}

wyznacza punkty przecięcia prostej i paraboliparabolaparaboli, o ile takie istnieją.

Przykład 2

Rozwiążemy układ równańukład równań z dwiema niewiadomymi i podamy jego interpretację geometryczną:

a) $\{\begin{cases} y = x^{2} + x - 2 \\ y = x - 2 \end{cases}$

Rozwiązanie:

Podany układ równań jest układem równań drugiego stopnia z dwoma niewiadomymi.

Możemy narysować wykresy podanych równań i znaleźć punkt przecięcia, o ile taki istnieje.

Wyznaczmy miejsca przecięcia z osią odciętych, paraboli opisanej równaniem $y = x^{2} + x - 2$ .

Rozpoczniemy od wyznaczania wyróżnika trójmianu kwadratowego:

$Δ = b^{2} - 4 a c = 1 - 4 \cdot (- 2) = 1 + 8 = 9$ , $\sqrt{Δ} = 3$ .

Wówczas

$x_{1} = \frac{- b - \sqrt{Δ}}{2 a} = \frac{- 1 - 3}{2} = - 2$ ,

$x_{2} = \frac{- b + \sqrt{Δ}}{2 a} = \frac{- 1 + 3}{2} = 1$ .

Wynika stąd, że parabola przecina oś $X$ w punktach $(- 2, 0)$ oraz $(1, 0)$ .

Parabola przecina oś $Y$ w punkcie $(0, - 2)$ .

Z równania kierunkowego prostej $y = x - 2$ odczytujemy, że prosta przecina oś $Y$ w punkcie $(0, - 2)$ oraz oś $X$ w punkcie $(2, 0)$ .

Punktem wspólnym obu wykresów jest punkt $P = (0, - 2)$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

RNPQ0MRfID81d

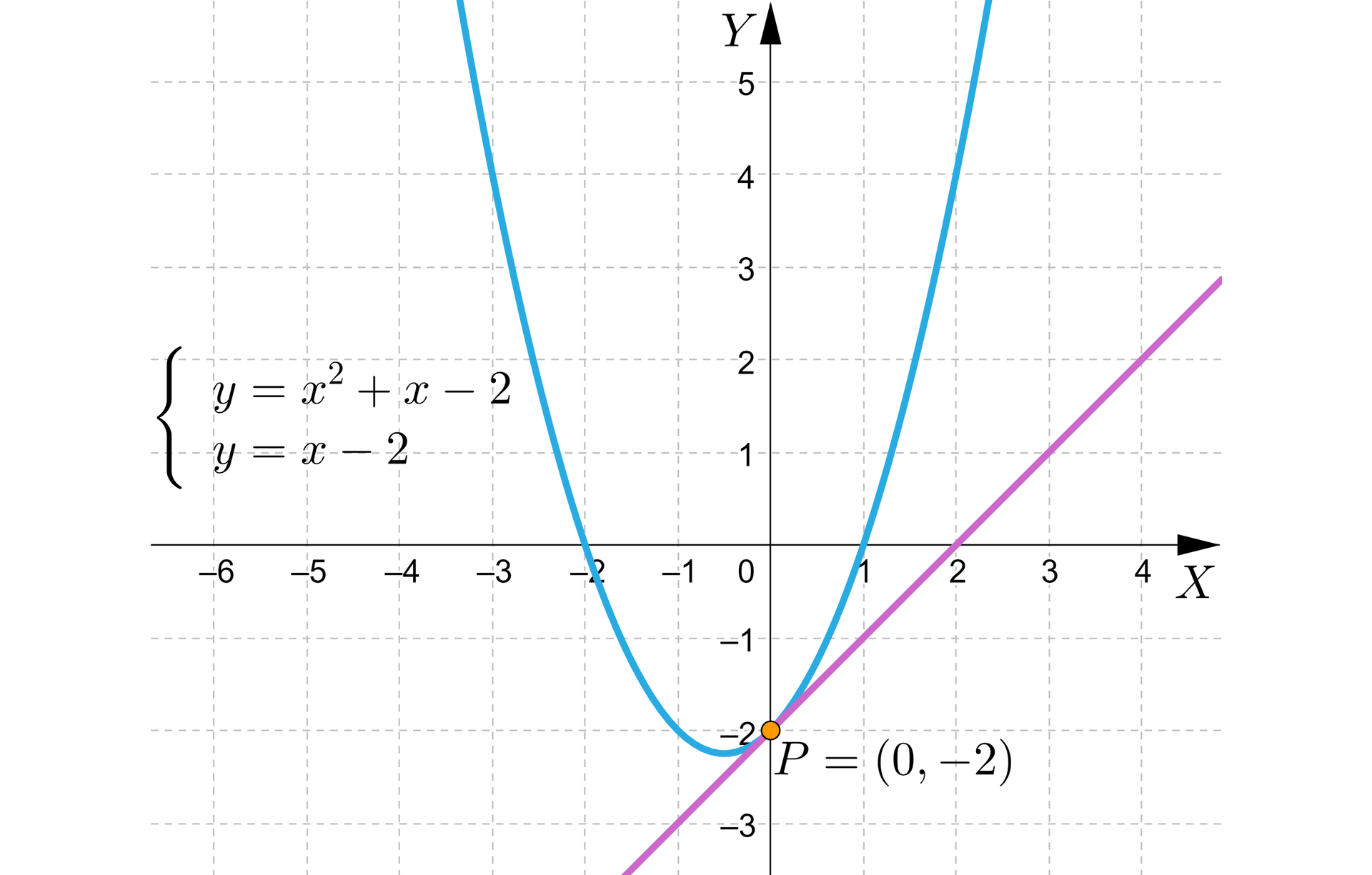
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do czterech, oraz z pionową osią Y od minus trzech do pięciu. Na płaszczyźnie narysowano wykresy dwóch funkcji. Wykres funkcji pierwszej to parabola o wierzchołku w punkcie P o współrzędnych 0;-2. Ramiona paraboli skierowane są w górę, oraz przecinają oś X w punkcie x=-2, oraz x=1. Wykres funkcji drugiej, stanowi linia przechodząca przez punkt P, oraz punkt o współrzędnych (2;0). Obok wykresu zapisano układ dwóch równań. Równanie pierwsze y=x2+x-2. Równanie drugie y=x-2.

Odpowiedź:

Rozwiązaniem układu równań jest para liczb, będąca odpowiednio współrzędnymi punktu $P = (0, - 2)$ .

b) $\{\begin{cases} y = x^{2} + x - 2 \\ y = x - 1 \end{cases}$

Rozwiązanie:

Zauważmy, że równanie paraboli jest takie samo jak w podpunkcie a), czyli wykres przecina oś $X$ w punktach $(- 2, 0)$ oraz $(1, 0)$ a oś $Y$ w punkcie $(0, - 2)$ .

Aby wykonać dokładny rysunek paraboli w układzie współrzędnych obliczamy współrzędne wierzchołka, czyli

$p = \frac{- b}{2 a} = \frac{- 1}{2}$ oraz $q = \frac{- Δ}{4 a} = \frac{- 9}{4} = - 2 \frac{1}{4}$ , bo

$Δ = b^{2} - 4 a c = 1 - 4 \cdot (- 2) = 1 + 8 = 9$ .

Z równania kierunkowego prostej $y = x - 1$ odczytujemy, że prosta przecina oś odciętych dla $x = 1$ oraz przecina oś $Y$ w punkcie $(0, - 1)$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

R1Vuoaf8bzuVS

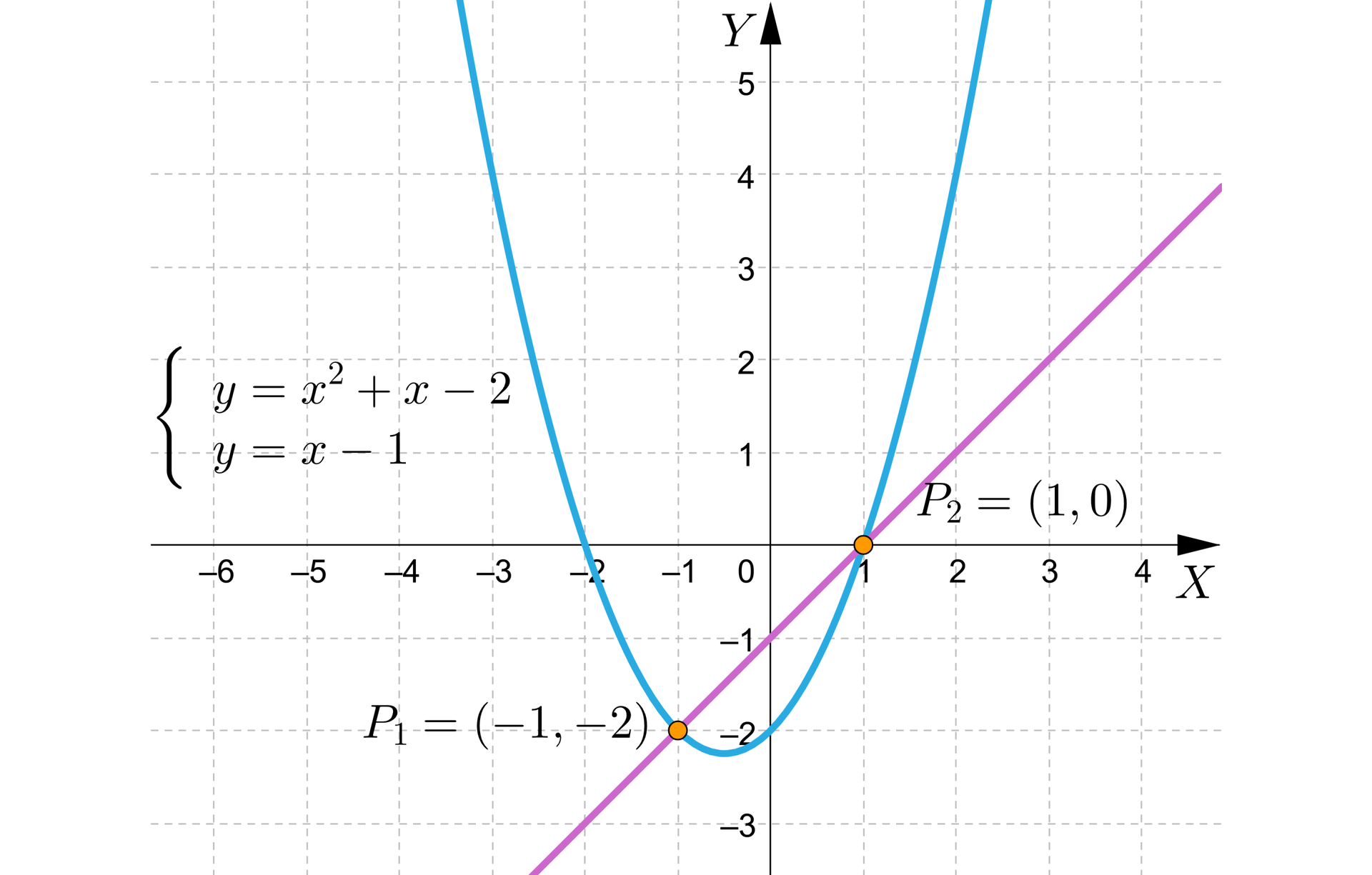
Widać z rysunku, że parabola i prosta mają dwa punkty wspólne. Współrzędne tych punktów odczytujemy z wykresu, czyli $P_{1} = (- 1, - 2)$ oraz $P_{2} = (1, 0)$ .

Sprawdzamy, czy rozwiązując podany układ algebraicznie dostaniemy takie samo rozwiązanie.

Wyznaczamy niewiadomą $y$ z drugiego równania i wyrażenie $x - 1$ wstawiamy w miejsce $y$ do pierwszego równania:

$\{\begin{cases} x^{2} + x - 2 = x - 1 \\ y = x - 1 . \end{cases}$

porządkujemy pierwsze równanie skąd otrzymujemy:

$\{\begin{cases} x^{2} - 1 = 0 \\ y = x - 1 . \end{cases}$

Otrzymaliśmy w ten sposób równanie kwadratowe $x^{2} - 1 = 0$ , które rozwiązujemy następująco

$x^{2} = 1$ ,

$|x| = 1$ ,

$x_{1} = - 1$ i $x_{2} = 1$ .

Wyznaczamy odpowiednio niewiadomą $y$ dla $x_{1}$ i $x_{2}$ , czyli

$y_{1} = - 1 - 1 = - 2$ oraz $y_{2} = 1 - 1 = 0$

Rozwiązaniem układu równań są pary liczb postaci $(- 1, - 2)$ oraz $(1, 0)$ .

Odpowiedź:

Rozwiązaniem układu równań są dwie pary liczb, będące współrzędnymi punktów, odpowiednio $P_{1} = (- 1, - 2)$ oraz $P_{2} = (1, 0)$ .

Przypomnijmy, że okrągokrągokrąg o środku $S = (a, b)$ i promieniu $r > 0$ ma równanie:

{(x - a)}^{2} + {(y - b)}^{2} = r^{2}

Układ równań opisujący prostą i okrąg

\{\begin{cases} A x + B y + C = 0 \\ {(x - a)}^{2} + {(y - b)}^{2} = r^{2} \end{cases}

ma:

dokładnie dwa rozwiązania wtedy i tylko wtedy, gdy prosta przecina okrąg w dwóch punktach,

dokładnie jedno rozwiązanie wtedy i tylko wtedy, gdy prosta jest styczna do okręgu

nie ma rozwiązań wtedy i tylko wtedy, gdy prosta i okrąg > nie mają punktów wspólnych.

Przykład 3

Rozwiążemy układ równań z dwiema niewiadomymi, gdzie jedno z równań jest równaniem okręgu, a drugie jest równaniem liniowym, wykorzystując interpretację geometryczną:

a) $\{\begin{cases} x^{2} + y^{2} = 4 \\ x - y - 4 = 0 \end{cases}$

Rozwiązanie:

Pierwsze równanie opisuje okrąg o środku w punkcie $S = (0, 0)$ oraz promieniu $r = 2$ .

Przekształcamy równanie prostej w postaci ogólnej do równania prostej w postaci kierunkowej:

$- y = - x + 4$ .

Mnożąc stronami przez $(- 1)$ dostajemy

$y = x - 4$ .

Z równania kierunkowego prostejprostaprostej odczytujemy, że prosta przecina oś $Y$ w punkcie $(0, - 4)$ oraz oś odciętych dla $x = 4$ .

Poniższy rysunek przedstawia ilustrację graficzną układu:

R1c5ZK5DgopBg

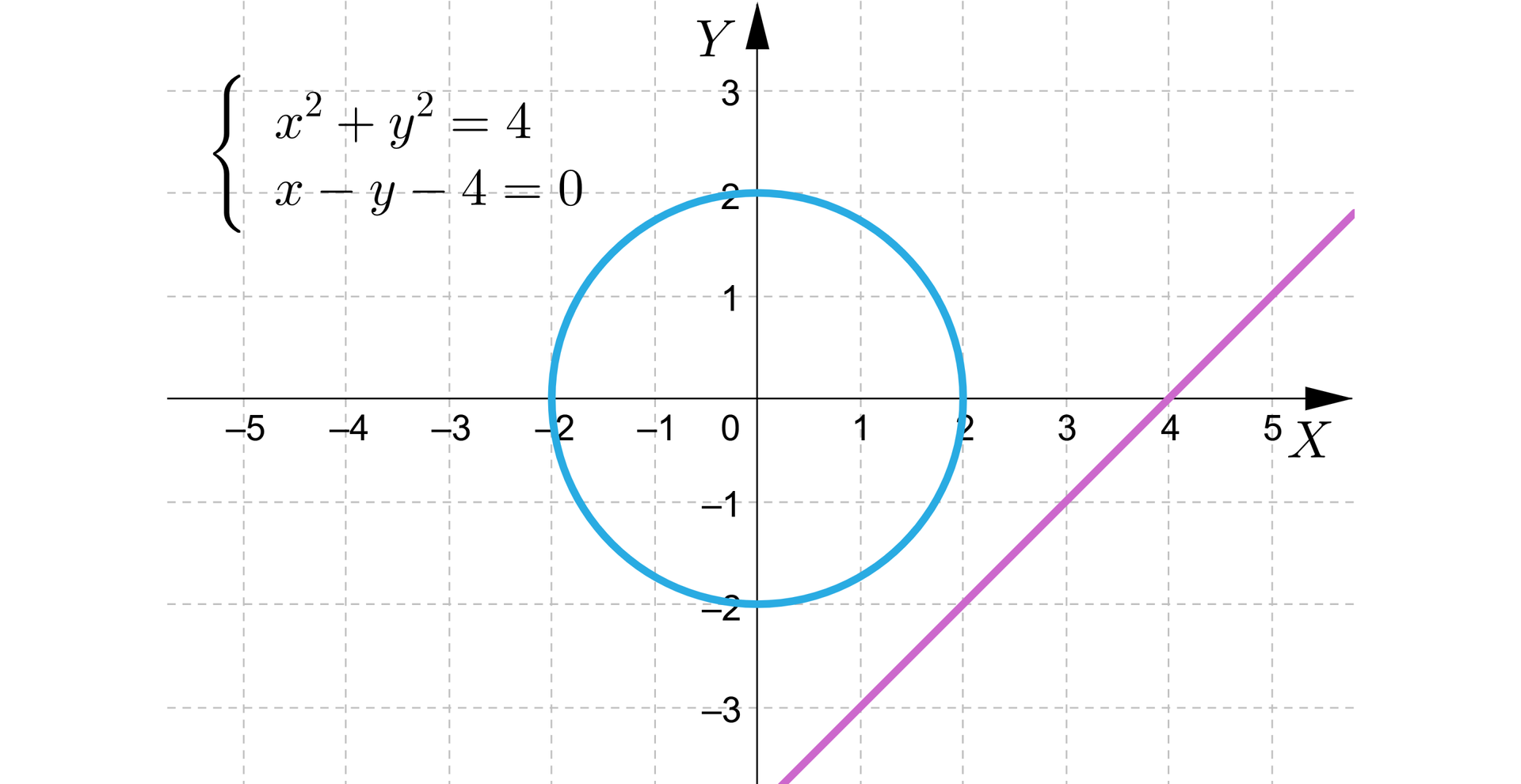
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do pięciu, oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie narysowano wykresy dwóch funkcji. Wykres funkcji pierwszej stanowi okrąg o środku w punkcie 0;0, oraz promieniu równym dwa. Wykres funkcji drugiej to prosta przechodząca przecinająca oś Y w punkcie 0;-4 oraz oś X dla x=4. Obok zapisano układ dwóch równań. Równanie pierwsze x2+y2=4. Równanie drugie x-y-4=0.

Wykresy nie posiadają punktów wspólnych, zatem układ równań nie ma rozwiązania.

Odpowiedź:

Układ nie posiada rozwiązań.

b) $\{\begin{cases} x^{2} + y^{2} = 4 \\ x - y - 2 \sqrt{2} = 0 \end{cases}$

Rozwiązanie:

Pierwsze równanie opisuje okrąg o środku w punkcie $S = (0, 0)$ i promieniu $r = 2$ .

Przekształcamy równanie prostej w postaci ogólnej do równania prostej w postaci kierunkowej:

$- y = - x + 2 \sqrt{2}$ .

Mnożąc obie strony przez $(- 1)$ dostajemy

$y = x - 2 \sqrt{2}$ .

Z równania kierunkowej prostej odczytujemy, że prosta przecina oś $Y$ w punkcie $(0, - 2 \sqrt{2})$ i oś odciętych dla $x = 2 \sqrt{2}$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

R15Fo31KAAiT6

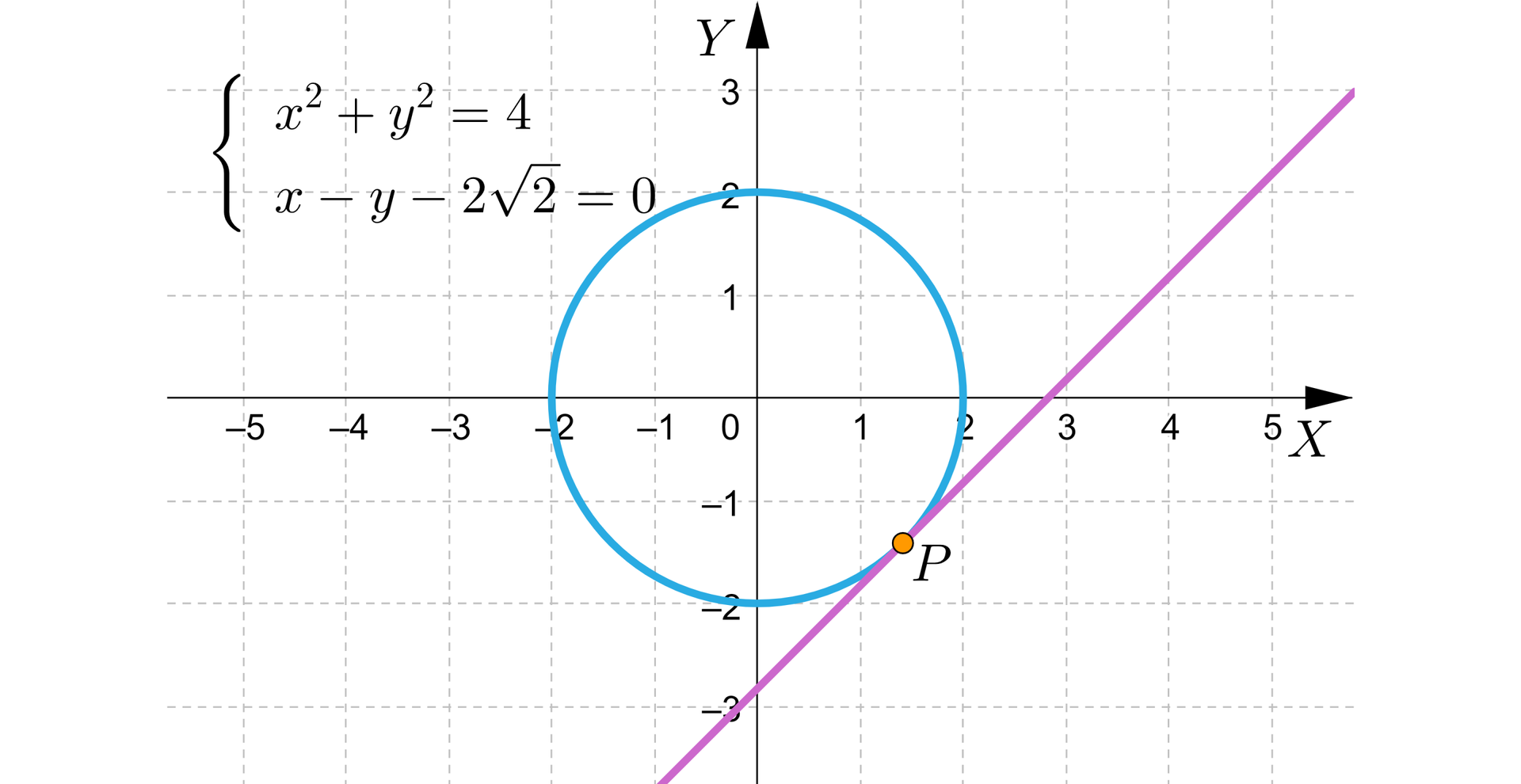
Odczytujemy z rysunku, że wykresy posiadają jeden punkt wspólny - prosta jest styczna do okręgu w punkcie $P$ .

Współrzędne punktu $P$ są trudne do odczytania, więc wyznaczamy rozwiązanie układu metodą algebraiczną.

Korzystając z postaci równania kierunkowego prostej, zapisujemy układ równań następująco:

$\{\begin{cases} x^{2} + y^{2} = 4 \\ y = x - 2 \sqrt{2} . \end{cases}$

Wyrażenie $x - 2 \sqrt{2}$ wstawiamy w miejsce $y$ do pierwszego równania:

$\{\begin{cases} x^{2} + {(x - 2 \sqrt{2})}^{2} = 4 \\ y = x - 2 \sqrt{2} \end{cases}$

i porządkujemy pierwsze równanie, korzystając ze wzorów skróconego mnożenia:

$\{\begin{cases} x^{2} + x^{2} - 4 \sqrt{2} x + 8 = 4 \\ y = x - 2 \sqrt{2} \end{cases}$ ,

skąd otrzymujemy

$\{\begin{cases} 2 x^{2} - 4 \sqrt{2} x + 4 = 0 \\ y = x - 2 \sqrt{2 .} \end{cases}$

Rozwiążemy równanie kwadratowe $2 x^{2} - 4 \sqrt{2} x + 4 = 0$ , zaczynając od wyznaczenia wyróżnika trójmianu kwadratowego

$Δ = b^{2} - 4 a c = 32 - 32 = 0$ .

Wynika stąd, że istnieje tylko jedno rozwiązanie równania kwadratowego $x_{0} = \frac{- b}{2 a} = \frac{4 \sqrt{2}}{4} = \sqrt{2}$ .

Wyznaczamy wartość drugiej niewiadomej $y_{0} = \sqrt{2} - 2 \sqrt{2} = - \sqrt{2}$ .

Zatem prosta $x - y - 2 \sqrt{2} = 0$ jest styczna do okręgu o równaniu $x^{2} + y^{2} = 4$ w punkcie $P = (\sqrt{2}, - \sqrt{2})$ .

Odpowiedź:

Rozwiązaniem układu równań jest para liczb $\{\begin{cases} x = \sqrt{2} \\ y = - \sqrt{2} \end{cases}$ .

c) $\{\begin{cases} x^{2} + y^{2} = 4 \\ x - y - 2 = 0 \end{cases}$

Rozwiązanie:

Pierwsze równanie opisuje okrąg o środku w punkcie $S = (0, 0)$ i promieniu $r = 2$ .

Przekształcamy równanie prostej w postaci ogólnej do równania prostej w postaci kierunkowej i otrzymujemy

$y = x - 2$ .

Z równania prostej w postaci kierunkowej odczytujemy, że prosta przecina oś $Y$ w punkcie $(0, - 2)$ a oś odciętych dla $x = 2$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

RNCLvIBFUJcEv

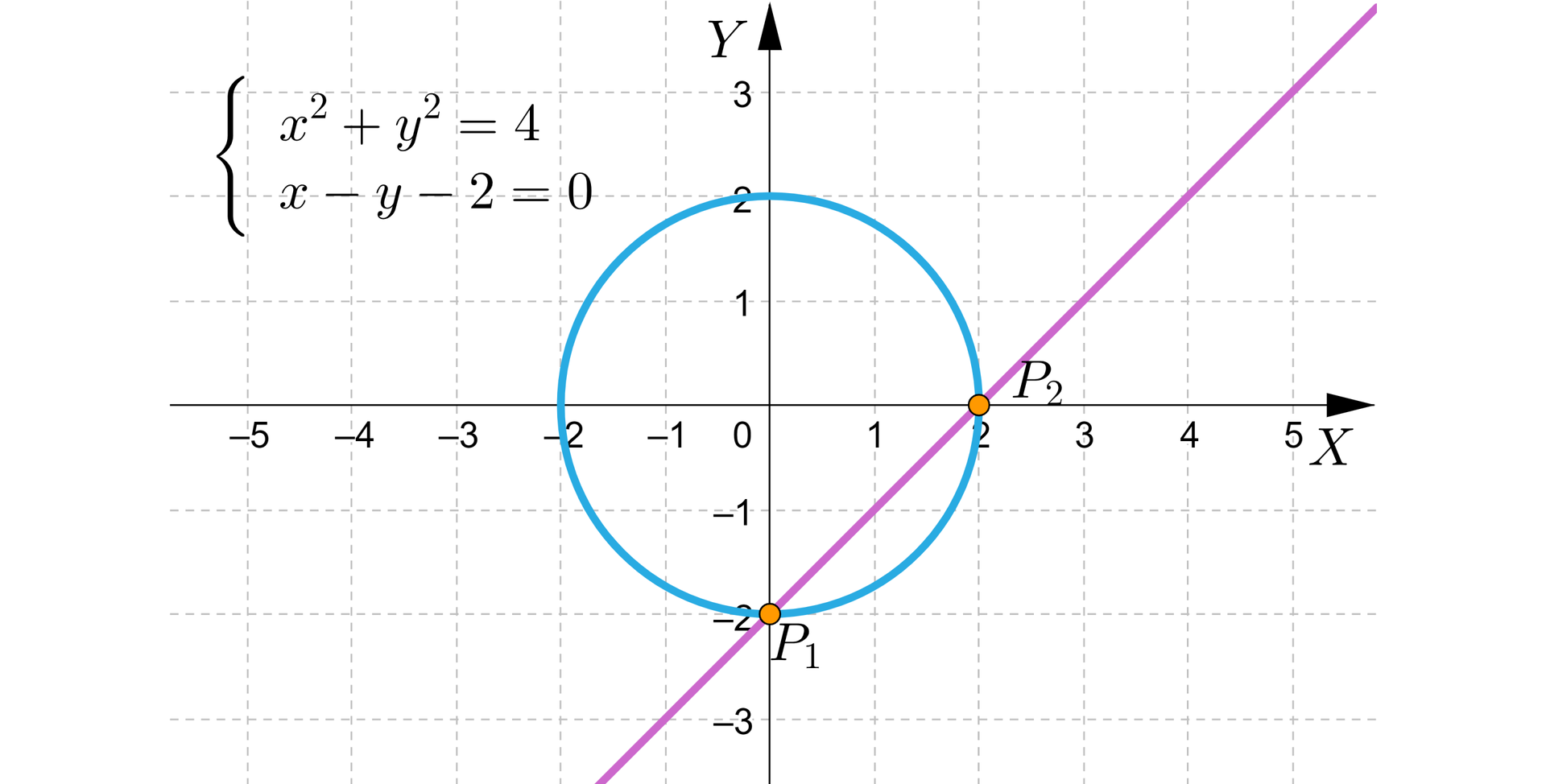
Odczytujemy z wykresu, że prosta przecina okrąg w dwóch punktach: $P_{1} = (0, - 2)$ i $P_{2} = (2, 0)$ . Wynika stąd, że układ równań ma dwa rozwiązania.

Przejdziemy do rozwiązania podanego układu równań metodą algebraiczną.

Skorzystamy z postaci równania kierunkowego prostej, aby zapisać układ równańukład równań

$\{\begin{cases} x^{2} + y^{2} = 4 \\ y = x - 2 . \end{cases}$

Z drugiego równania układu wyznaczamy $y$ i wyrażenie $x - 2$ wstawiamy w miejsce $y$ do pierwszego równania:

$\{\begin{cases} x^{2} + {(x - 2)}^{2} = 4 \\ y = x - 2 \end{cases}$

porządkujemy pierwsze równanie stosując wzór skróconego mnożenia

$\{\begin{cases} x^{2} + x^{2} - 4 x + 4 = 4 \\ y = x - 2 \end{cases}$

i stąd otrzymujemy

$\{\begin{cases} 2 x^{2} - 4 x = 0 \\ y = x - 2 . \end{cases}$

Rozwiązujemy równanie kwadratowe $2 x^{2} - 4 x = 0$ korzystając z wyłączenia czynnika przed nawias, czyli

$2 x (x - 2) = 0$ ,

$x_{1} = 0$ i $x_{2} = 2$ .

Wyznaczamy odpowiednie wartości niewiadomej $y$ dla $x_{1}$ oraz $x_{2}$ , czyli $y_{1} = 0 - 2 = - 2$ i $y_{2} = 2 - 2 = 0$ . Otrzymujemy w ten sposób dwie pare liczb, które pokrywają się z odczytanymi z wykresu współrzędnymi punktów.

Odpowiedź:
Rozwiązanie układu równań: $\{\begin{cases} x = 0 \\ y = - 2 \end{cases} \lor \{\begin{cases} x = 2 \\ y = 0 \end{cases}$ .

Wykresem równania $x y = a$ określonego dla $x \in ℝ ∖ \{0\}$ oraz $a \neq 0$ na płaszczyźnie jest hiperbolahiperbolahiperbola, więc układ opisujący odpowiednio hiperbolę i prostą

\{\begin{cases} A x + B y + C = 0 \\ x y = a \end{cases}

ma:

dokładnie dwa rozwiązania wtedy i tylko wtedy, gdy prosta przecina hiperbolę w dwóch punktach,

dokładnie jedno rozwiązanie wtedy i tylko wtedy, gdy prosta ma jeden punkt wspólny z hiperbolą,

nie ma rozwiązań wtedy i tylko wtedy, gdy prosta i hiperbola nie mają punktów wspólnych.

Przykład 4

Rozwiążemy układ równań z dwiema niewiadomymi, gdzie jedno z równań jest równaniem hiperboli, a drugie jest równaniem liniowym, wykorzystując interpretację geometryczną:

a) $\{\begin{cases} x y = 1 \\ 4 x + y = 0 \end{cases}$

Rozwiązanie:

Równanie hiperboli przekształcamy do postaci $y = \frac{1}{x}$ . Asymptotami wykresu są proste o równaniu $x = 0$ oraz $y = 0$ .

Równanie prostej w postaci ogólnej przekształcamy do równania prostej w postaci kierunkowej $y = - 4 x$ .

Prosta przechodzi przez początek układu współrzędnych. Dla dokładnego narysowania wykresu potrzebny jest drugi punkt, więc dla $x = 1$ otrzymujemy punkt o współrzednych $(1, - 4)$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

R1OXIXjosLxIF

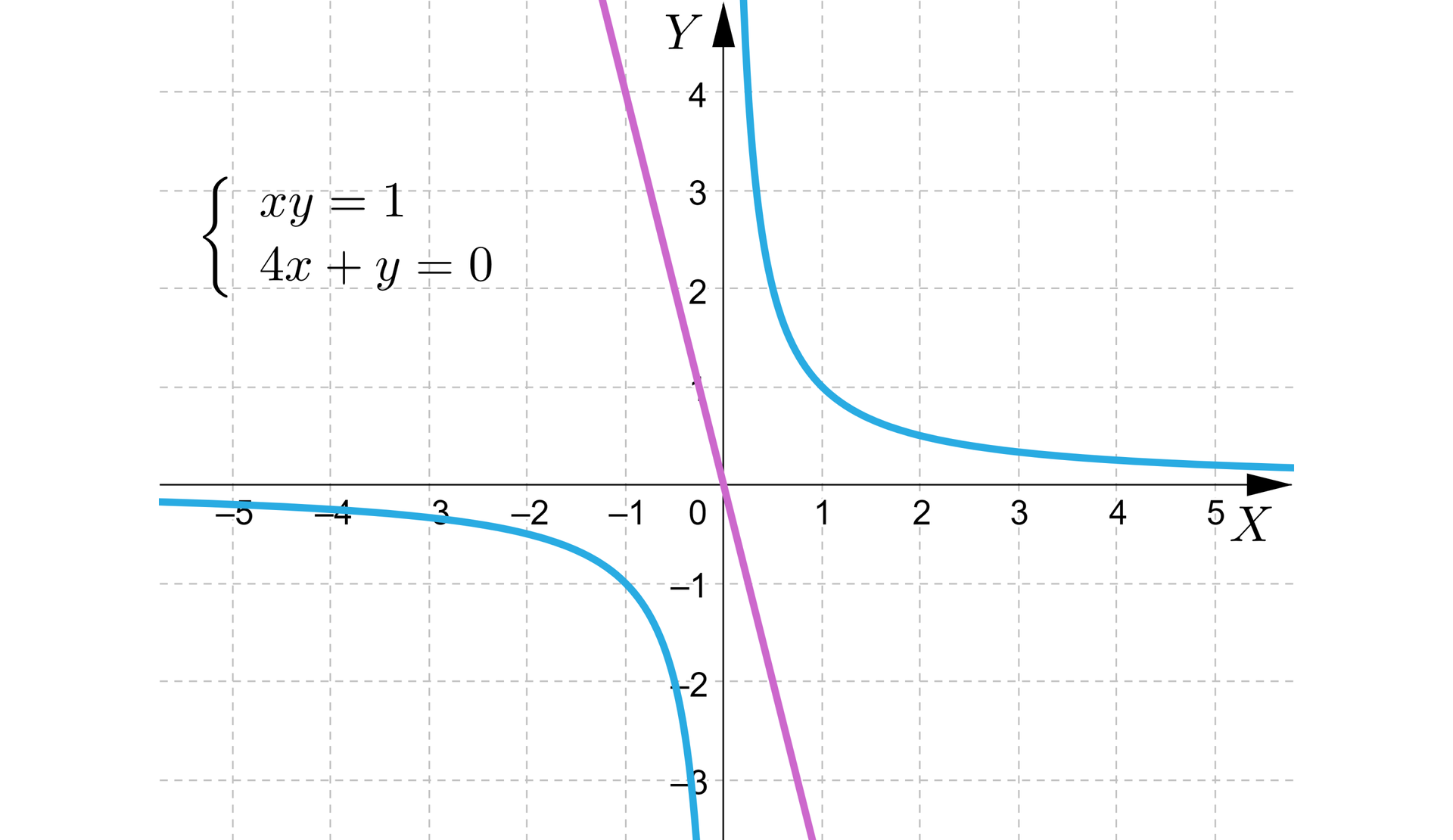
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do pięciu, oraz z pionową osią Y od minus trzech do czterech. Na płaszczyźnie narysowano wykresy dwóch funkcji. Wykres funkcji pierwszej to hiperbola, której gałęzie znajdują się w pierwszej oraz trzeciej ćwiartce układu współrzędnych. Wykres funkcji drugiej stanowi prosta, przechodząca przez środek układu współrzędnych, oraz punkt o współrzędnych -1;4. Obok zapisano układ dwóch równań. Równanie pierwsze xy=1. Równanie drugie 4x+y=0.

Odczytujemy z rysunku, że wykresy prostej i hiperboli nie przecinają się. Wynika stąd, że układ nie ma rozwiązań.

Odpowiedź:
Układ jest sprzeczny.

b) $\{\begin{cases} x y = 1 \\ 4 x + y - 4 = 0 \end{cases}$

Rozwiązanie:

Równanie hiperboli przekształcamy do postaci $y = \frac{1}{x}$ . Asymptoptami wykresu są proste o równaniu $x = 0$ oraz $y = 0$ .

Równanie prostejprostaprostej w postaci ogólnej przekształcamy do równania prostej w postaci kierunkowej $y = - 4 x + 4$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

RTtMWl9FMMQoQ

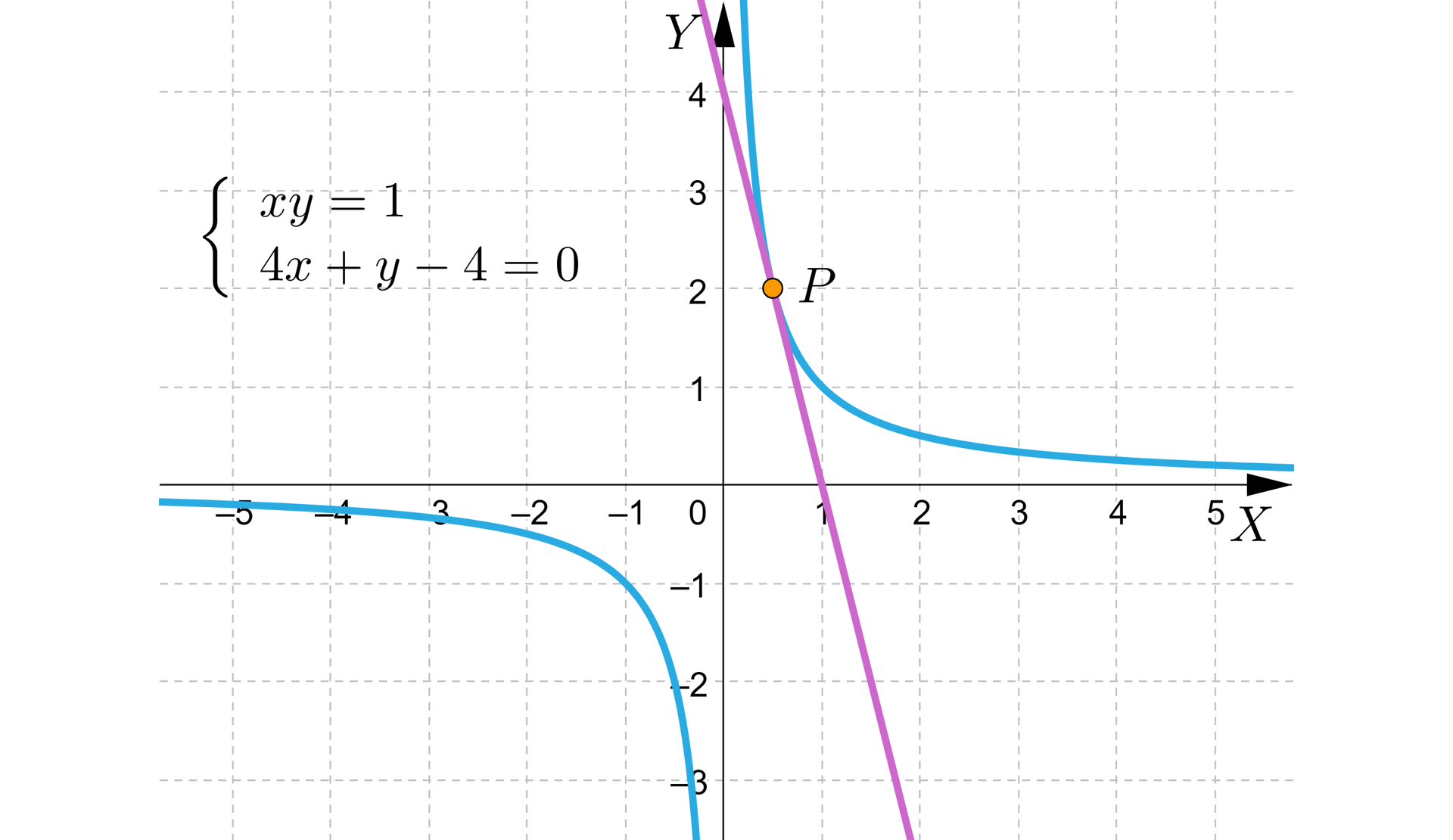
Z podanego rysunku możemy odczytać, że punktem wspólnym hiperboli i prostej jest punkt $P = (\frac{1}{2}, 2)$ .

Sprawdzamy, czy poprawnie odczytaliśmy współrzedne punktu rozwiązując układ równań algebraicznie. Zapisujemy układ równań korzystając z równania kierunkowej prostej:

$\{\begin{cases} x y = 1 \\ y = - 4 x + 4 . \end{cases}$

Wyznaczamy niewiadomą $y$ z drugiego równania i wyrażenie $- 4 x + 4$ wstawiamy w miejsce $y$ do pierwszego równania

$\{\begin{cases} x (- 4 x + 4) = 1 \\ y = - 4 x + 4 . \end{cases}$

Porządkujemy pierwsze równanie skąd otrzymujemy

$\{\begin{cases} - 4 x^{2} + 4 x = 1 \\ y = - 4 x + 4 . \end{cases}$

Rozwiązujemy równanie kwadratowe $- 4 x^{2} + 4 x - 1 = 0$ .

Wyłączamy $(- 1)$ przed nawias i otrzymujemy $- (4 x^{2} - 4 x + 1) = 0$ .

Korzystamy ze wzoru skróconego mnożenia aby zapisać równanie kwadratowe w postaci $- {(2 x - 1)}^{2} = 0$ .

Rozwiązaniem równania jest liczba $x = \frac{1}{2}$ . Wyznaczamy wartość drugiej niewiadomej

$y = - 4 \cdot \frac{1}{2} + 4 = - 2 + 4 = 2$ .

Odczytane współrzędne punktu $P$ pokrywają się z algebraicznym rozwiązaniem.

Odpowiedź:
Rozwiązaniem układu równań jest para liczb:

$\{\begin{cases} x = \frac{1}{2} \\ y = 2 . \end{cases}$

Prosta o równaniu $4 x + y - 4 = 0$ ma z hiperbolą $x y = 1$ jeden punkt wspólny $P = (\frac{1}{2}, 2)$ .

c) $\{\begin{cases} x y = 1 \\ 4 x + y - 5 = 0 \end{cases}$

Rozwiązanie:

Równanie hiperboli przekształcamy do postaci $y = \frac{1}{x}$ . Asymptoptami wykresu są proste o równaniu $x = 0$ oraz $y = 0$ .

Równanie prostej w postaci ogólnej przekształcamy do równania prostej w postaci kierunkowej

$y = - 4 x + 5$ .

Poniższy rysunek przedstawia ilustrację graficzną układu.

RtLryV8u4D4x0

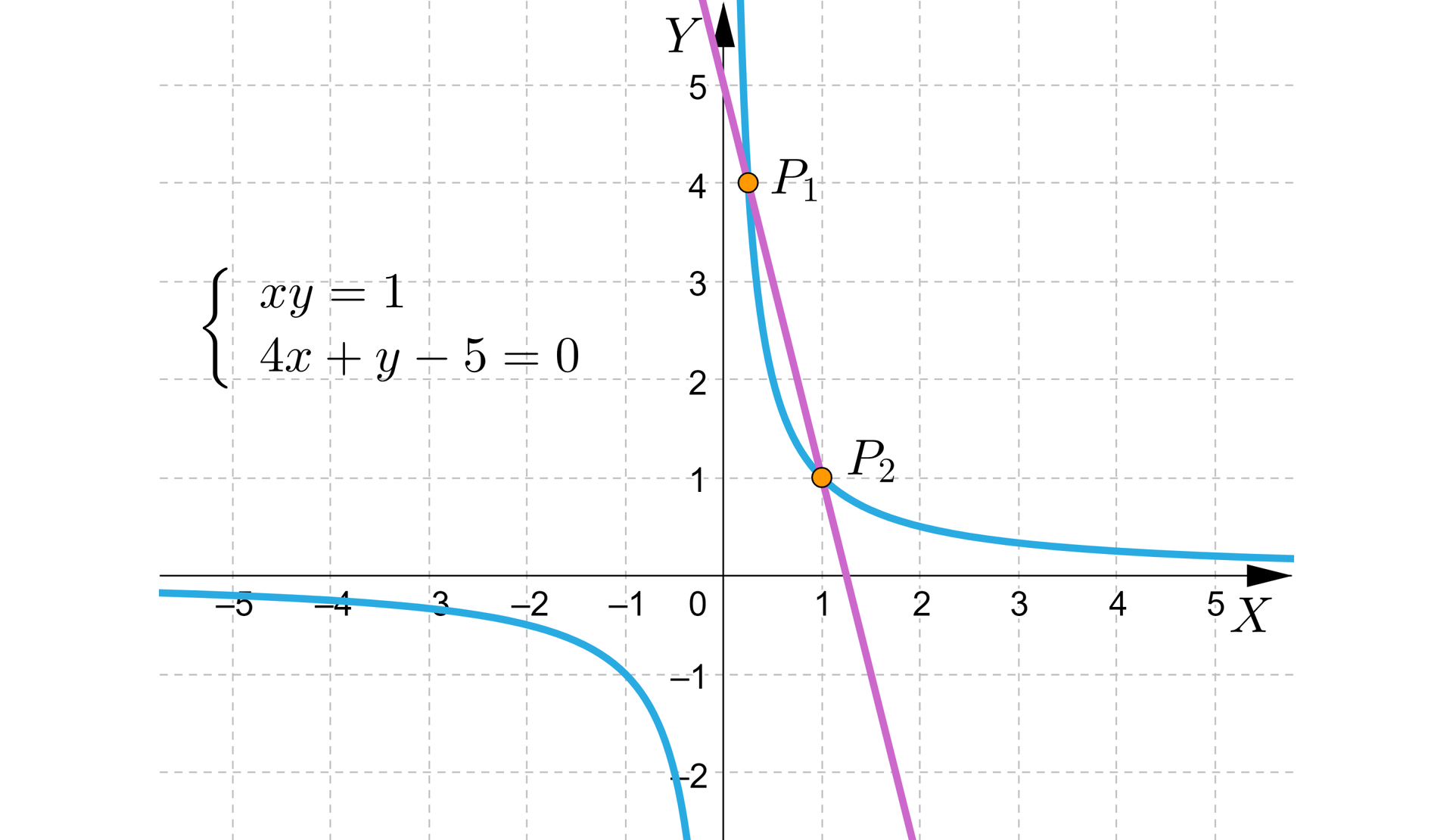
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do pięciu, oraz z pionową osią Y od minus dwóch do pięciu. Na płaszczyźnie narysowano wykresy dwóch funkcji. Wykres funkcji pierwszej to hiperbola, której gałęzie znajdują się w pierwszej oraz trzeciej ćwiartce układu współrzędnych. Wykres przechodzi przez punkt P1 o współrzędnych 14;1, oraz punkt P2 o współrzędnych 1;1. Wykres funkcji drugiej stanowi prosta przechodząca przez punkt P1, oraz P2. Obok wykresu zapisano układ dwóch równań. Równanie pierwsze xy=1. Równanie drugie 4x+y-5=0.

Z rysunku odczytujemy współrzędne punktów wspólnych hiperboli i prostej $P_{1} = (\frac{1}{4}, 1)$ oraz $P_{2} = (1, 1)$ .

Sprawdzamy, czy poprawnie odczytaliśmy współrzedne punktów rozwiązując układ metodą algebraiczną. Korzystamy z równania prostej w postaci kierunkowej aby zapisać układ równań

$\{\begin{cases} x y = 1 \\ y = - 4 x + 5 . \end{cases}$

Z drugiego równania wyznaczamy $y$ i wyrażenie $- 4 x + 5$ wstawiamy w miejsce $y$ do pierwszego równania

$\{\begin{cases} x (- 4 x + 5) = 1 \\ y = - 4 x + 5 . \end{cases}$

Porządkujemy pierwsze równanie skąd otrzymujemy

$\{\begin{cases} - 4 x^{2} + 5 x = 1 \\ y = - 4 x + 5 . \end{cases}$

Rozwiążemy równanie kwadratowe $- 4 x^{2} + 5 x = 1$ zaczynając od przeniesienia składnika liczbowego na lewą stronę, czyli

$- 4 x^{2} + 5 x - 1 = 0$ .

Liczymy wyróżnik trójmianu kwadratowego

$Δ = b^{2} - 4 a c = 25 - 4 \cdot (- 4) \cdot (- 1) = 9$ , stąd $\sqrt{Δ} = 3$ .

Rozwiązaniami równania kwadratowego są

$x_{1} = \frac{- b - \sqrt{Δ}}{2 a} = \frac{- 5 - 3}{- 8} = 1$ oraz $x_{2} = \frac{- b + \sqrt{Δ}}{2 a} = \frac{- 5 + 3}{- 8} = \frac{1}{4}$ .

Wyznaczamy wartości niewiadomej $y_{1} = - 4 + 5 = 1$ oraz $y_{2} = - 1 + 5 = 4$ .

Rozwiązania pokrywają się ze współrzędnymi punktów $P_{1}$ i $P_{2}$ .

Odpowiedź:

Rozwiązaniem układu równań są dwie pary liczb $(\frac{1}{4}, 4)$ i $(1, 1)$ .

Słownik

układ równań drugiego stopnia z dwiema niewiadomymi

układ dwóch równań z dwiema niewiadomymi, z których co najmniej jedno jest stopnia drugiego

parabola

parabola jest wykresem funkcji kwadratowej:

f (x) = a x^{2} + b x + c

a \neq 0

okrąg

okrąg to zbiór punktów płaszczyzny, których odległość od ustalonego punktu $S$ , zwanego środkiem okręgu jest równa ustalonej liczbie $r$ , zwanej promieniem okręgu; równaniem okręgu na płaszczyźnie jest

{(x - a)}^{2} + {(y - b)}^{2} = r^{2}

gdzie $a$ i $b$ są współrzędnymi środka okręgu, a $r$ jest jego promieniem

hiperbola

hiperbolą nazywamy zbiór punktów płaszczyzny spełniających równanie $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ , $a$ , $b > 0$ ; w szczególności hiperbola jest obrazem krzywej opisanej równaniem $x y = k$ określonym dla $x \in ℝ ∖ \{0\}$ oraz $k \neq 0$

prosta

prostą nazywamy zbiór punktów opisanych równaniem ogólnym

A x + B y + C = 0

gdzie $A$ i $B$ nie mogą być jednocześnie równe zeru; w szczególności prosta jest wykresem funkcji liniowej $f (x) = a x + b$ , gdzie $a \neq 0$ ; równanie postaci $y = a x + b$ nazywamy równaniem kierunkowym prostej

Wprowadzenie

Animacja

Interpretacja geometryczna układów równań drugiego stopnia

Słownik