Okrąg to zbiór punktów płaszczyzny, które są równo oddalone od jednego wybranego punktu, zwanego środkiem okręgu.

Popatrzmy na poniższy obrazek i przypomnijmy, jakie ważne pojęcia z nim się wiążą.

RRT3c57VejT5v

Ilustracja przedstawia okrąg o środku O i promieniu r; Narysowano dwie styczne do okręgu przecinające się w punkcie S. Jedna z prostych jest styczna do okręgu w punkcie P, a druga w punkcie Q. Narysowano też trzecią prostą przecinającą styczne, okrąg w punktach B i C oraz środek O. Zaznaczono dwie cięciwy: B A oraz B C, przy czym B C jest jednocześnie średnicą okręgu. W okręgu zaznaczono dwa promienie: O A oraz O Q, przy czym zaznaczono kąt prosty między promieniem O Q oraz odcinkiem S Q leżącym na stycznej.

Rozwiązanie

Jeżeli za środek okręgu przyjmiemy punkt $O$, to odległość tego środka od dowolnego punktu okręgu jest równa promieniowipromień okręgupromieniowi $r$:
($\left|OA\right|=r$, $\left|OB\right|=r$, $\left|OC\right|=r$).

Odcinek łączący dwa punkty okręgu, przechodzący przez jego środek nazywamy średnicą okręgu. Średnica okręguśrednica okręguŚrednica okręgu jest jednocześnie najdłuższą cięciwą i jej długość jest równa $2r$: $\left(\left|BC\right|=2r\right)$.

Cięciwa okręgucięciwa okręguCięciwa okręgu to dowolny odcinek łączący dwa punkty leżące na okręgu (na naszej ilustracji przykładowa cięciwa to odcinek $BA$).

Prosta zawierająca cięciwę to sieczna okręgusieczna okręgusieczna okręgu; ma ona dwa punkty wspólne z okręgiem (np. prosta przechodząca przez punkty $B$ i $C$ czy też prosta przechodząca przez punkty $A$ i $B$).

Prosta, która ma tylko jeden punkt wspólny z okręgiem, to styczna do okręgustyczna do okręgustyczna do okręgu. Z każdego punktu leżącego na zewnątrz okręgu można poprowadzić dwie styczne do tego okręgu (w naszym przykładzie to prosta przechodząca przez punkty $S$ i $P$ oraz prosta przechodząca przez punkty $S$ i $Q$).

Punkty $P$ i $Q$ to punkty styczności. Odcinki $SP$ i $SQ$ są równe.

Promień poprowadzony ze środka okręgu do punktu styczności jest prostopadły do stycznej w tym punkcie.

Jaką wspólną ważną własność mają okręgi? Jak ją odkryć?

Rozwiązanie

W każdym okręgu stosunek długości okręgu do jego średnicy równa się tej samej liczbie niewymiernej $\pi$, której najbardziej popularne i najczęściej używane przybliżenie to $3,14$.

Liczba $\pi$ to najsłynniejsza stała w matematyce; powinien ją znać każdy uczeń kończący szkołę podstawową. Historia tej liczby oraz historia określania coraz większej liczby cyfr w jej rozwinięciu dziesiętnym (czyli znajdowania coraz dokładniejszych jej przybliżeń) jest bogata i fascynująca. Możemy przeczytać o niej wiele w różnych źródłach. My skupmy się teraz na pytaniu: jak odkryć tę ważną własność okręgu?

Można przeprowadzić eksperyment matematyczny: zmierzyć (np. nitką, którą później rozwiniemy wzdłuż linii z podziałką) dowolny okrągły przedmiot, potem znaleźć jego średnicę (podpowiedź jak to zrobić w poniższym rysunku, gdzie dwie proste prostopadłe mogą być wyznaczone np. przez naroże stołu):

R1LtEOmiHg5X9

Ilustracja przedstawia cztery proste. Dwie z nich zaznaczono żółtą linią przerywaną, są one prostopadłe. Dwie kolejne narysowano niebieską linią przerywaną, one również są prostopadłe. Wszystkie cztery proste przecinają się w taki sposób, że wycinają na płaszczyźnie kwadrat. W kwadrat wpisany jest okrąg. Zaznaczono środek okręgu.

i podzielić dwie liczby przez siebie. Oczywiście pamiętajmy, że wykonanie jednego eksperymentu, czy też wykonanie wielu eksperymentów przez wielu uczniów nie stanowi dowodu, ale pozwala postawić hipotezę dotyczącą stosunku długości okręgu do jego średnicy.

Czy istnieją okręgi w szczególny sposób związane z innymi figurami geometrycznymi?

Rozwiązanie

Tak. Chyba najbardziej znanym przykładem jest tutaj okrąg dziewięciu punktów, czyli okrągokrągokrąg, który przechodzi przez dziewięć charakterystycznych punktów dowolnego trójkąta. Punktami tymi są: środki boków, spodki trzech wysokości oraz punkty dzielące na połowy trzy odcinki, które łączą wierzchołki tego trójkąta z jego ortocentrum, czyli punktem przecięcia jego wysokości:

RXiZo1vzmyHbq

Ilustracja przedstawia trójkąt, w którym wykreślono wysokości. Zaznaczono punkty na bokach figury, na które upuszczono wysokości. Zaznaczono także środki boków. Poprowadzono okrąg przez wyróżnione sześć punktów. Zaznaczono na okręgu również punkty, w których wysokości przecinają się z okręgiem.

Bardzo ciekawa jest historia odkrycia tego okręgu. W $1822$ roku Karl Wilhelm Feuerbach, którego nazwiskiem nazywa się czasem okrąg dziewięciu punktów, zauważył, że sześć charakterystycznych punktów trójkąta – środki boków oraz spodki wysokości – leżą na wspólnym okręgu. Krótko potem matematyk Olry Terquem niezależnie udowodnił istnienie takiego okręgu i jako pierwszy zauważył, że leżą na nim również środki odcinków łączących wierzchołki z ortocentrum. Jako pierwszy użył on nazwy „okrąg dziewięciu punktów”.

Czy na powierzchniach innych niż płaszczyzna też istnieją okręgi?

Rozwiązanie

Tak, na przykład na powierzchni kuli też można skonstruować okręgi. Przekrój kuli  płaszczyzną przechodzącą przez jej środek,  wyznacza na jej powierzchni okrąg wielki. Inne przekroje  wyznaczają na jej powierzchni okręgi o promieniach mniejszych niż promień kuli, jak obrazuje to poniższy rysunek.

R1a7xGijoHhR0

Ilustracja przedstawia kulę, wewnątrz której wykreślono dwa przekroje poprzeczne: jeden w górnej części kuli i drugi przechodzący przez środek O. Przekroje są kołami.

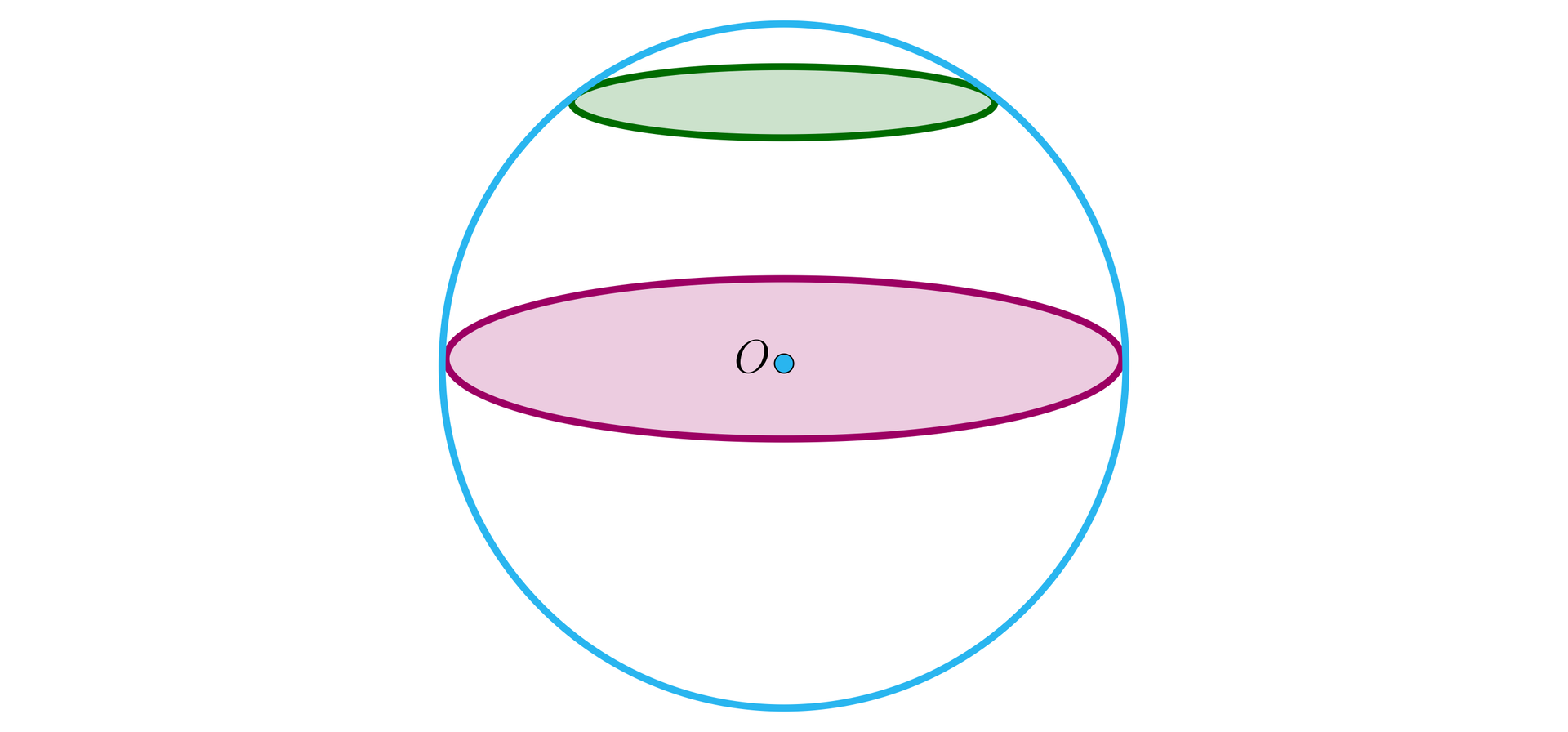
Okręgi widzimy też na globusie, który jest modelem kuli ziemskiej. Przykładem okręgu wielkiego jest równik, okręgów małych – równoleżniki:

R1XVrQ5u6GsBP

Ilustracja przedstawia Kulę Ziemską, na którą naniesiono okręgi będące równoleżnikami. Największy z nich podpisano jako równik.

Rozważmy sytuację: Mamy dwa różne punkty na płaszczyźnie: $A$ i $B$. Wiemy, że najkrótsza droga między nimi, to droga zawarta w prostej przechodzącej przez nie. Czy, gdy będziemy przedłużać w nieskończoność końce linii, w której zawarta jest najkrótsza droga między dwoma punktami, końce tej linii spotkają się gdziekolwiek?

Rozwiązanie

Odpowiedź jest prosta. Nie, ponieważ „długość” prostej jest nieskończona.

Trójkąt sferyczny to część powierzchni kuli, zawarta między trzema łukami kół wielkich przecinających się parami.

RG2miA5exyssz

Ilustracja przedstawia kulę, na której narysowano trzy równoleżniki znajdujące się pod różnymi kątami. Równoleżniki przecinają się, tworząc trójkąt sferyczny A B C. Różni się on tym od trójkąta płaskiego, że jest wypukły, a jego boki są nie odcinkami, a łukami.

zbiór wszystkich punktów na płaszczyźnie, których odległość od ustalonego punktu (zwanego środkiem okręgu), jest równa zadanej odległości (zwanej promieniem okręgu)

odległość punktu okręgu od jego środka

cięciwa przechodząca przez środek okręgu

odcinek łączący dwa punkty leżące na okręgu

prosta mająca z okręgiem dokładnie jeden punkt wspólny

prosta przecinająca okrąg w dwóch punktach

okrąg wielki na sferze

część powierzchni kuli, zawarta między trzema łukami kół wielkich przecinających się parami