Przeczytaj
Wzajemne położenie dwóch okręgów
Rozważmy dwa okręgi, których środkami są punkty i , a ich promienie są równe odpowiednio i .
Przyjmiemy wówczas następujące definicje.
Powiemy, że okręgi i są styczne zewnętrznie, jeżeli mają jeden punkt wspólny i koła ograniczone tymi okręgami nie mają żadnych innych punktów wspólnych. Punkt wspólny tych okręgów nazywamy ich punktem styczności.

Powiemy, że okręgi i są styczne wewnętrznie, jeżeli mają jeden punkt wspólny, a koła ograniczone tymi okręgami mają nieskończenie wiele punktów wspólnych.
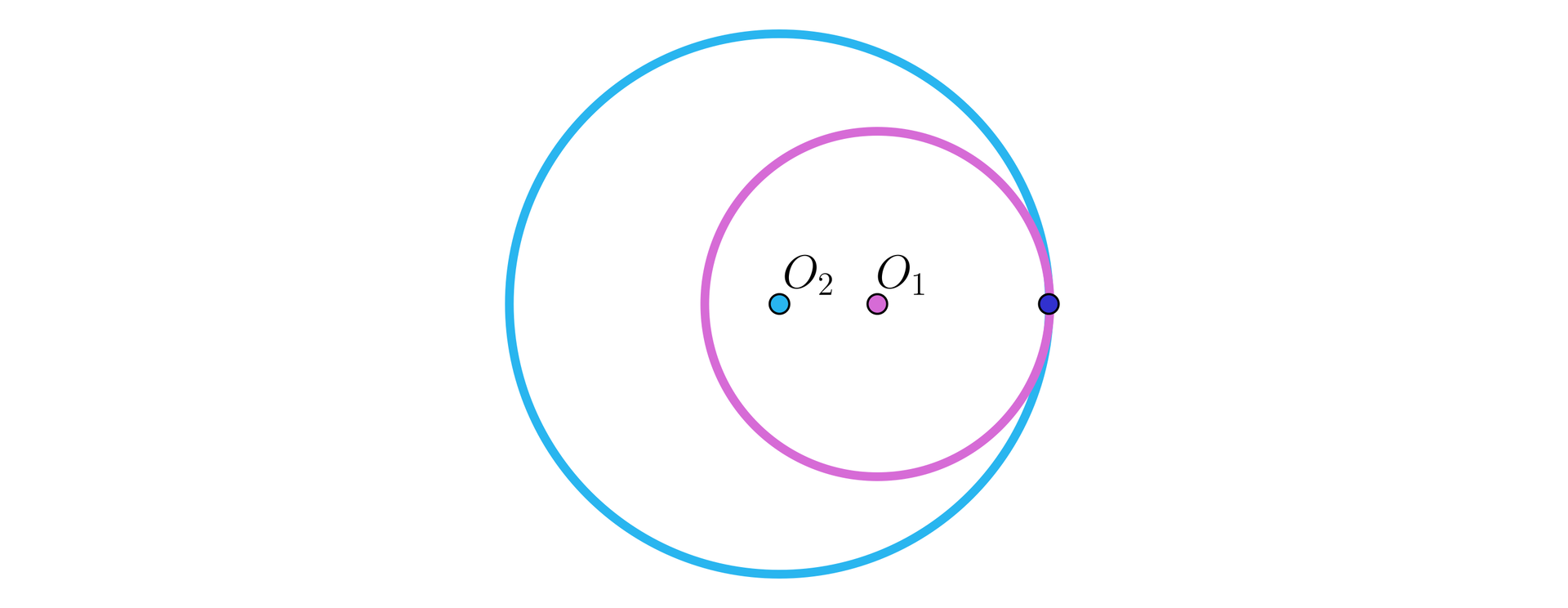
Zauważmy, że nie istnieją okręgi o równych promieniach, które byłyby styczne wewnętrznie.
Zauważmy, że okręgi mogą mieć dwa punkty wspólne – powiemy wówczas, że okręgi te przecinają się.
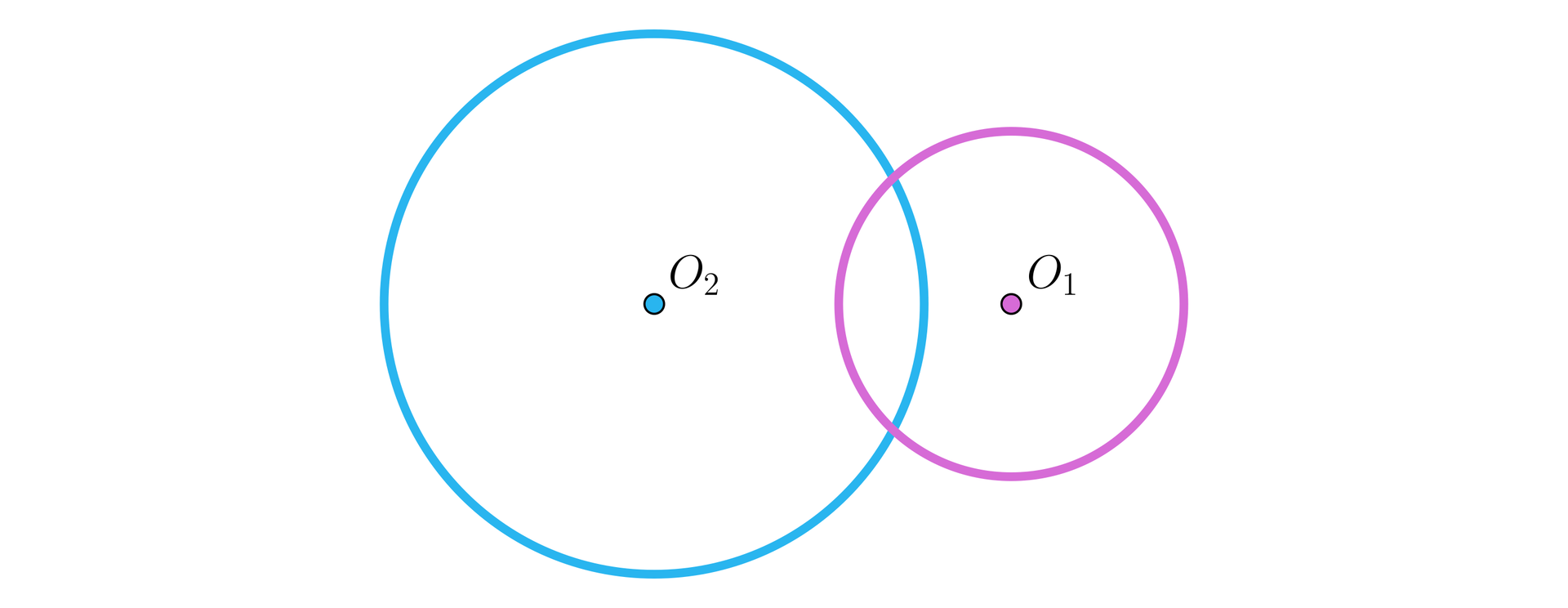
Dwa okręgi mogą nie mieć żadnego punktu wspólnego – mamy wówczas dwa istotnie różne położenia takich okręgów, podobnie jak w przypadku okręgów stycznych. Jednym z położeń jest takie, w którym koła ograniczone tymi okręgami nie mają punktów wspólnych – powiemy wówczas, że każdy z tych okręgów leży na zewnątrz drugiego.

Drugim położeniem, przy którym dwa okręgi nie mają punktów wspólnych jest takie, w którym koło, ograniczone jednym z okręgów, leży wewnątrz drugiego z kół.

Jeżeli jeden z okręgów leży wewnątrz drugiego z okręgów w taki sposób, że ich środki się pokrywają, to powiemy, ze okręgi te są współśrodkowe.
Wzajemne położenie dwóch okręgów charakteryzują poniższe twierdzenia, które ze względu na ich intuicyjny charakter, przyjmujemy bez dowodu.
Jeżeli odległość środków dwóch okręgów jest większa od sumy ich promieni, to każdy z tych okręgów leży na zewnątrz drugiego.
Jeżeli odległość środków dwóch okręgów jest równa sumie ich promieni, to okręgi te są styczne zewnętrznie.
Jeżeli odległość środków dwóch okręgów, o różnych promieniach, jest równa wartości bezwzględnej różnicy tych promieni, to okręgi te są styczne wewnętrznie.
Jeżeli odległość środków dwóch okręgów jest mniejsza od wartości bezwzględnej różnicy ich promieni, to okrąg o mniejszym promieniu leży wewnątrz okręgu o większym promieniu.
Jeżeli odległość środków dwóch okręgów jest większa od wartości bezwzględnej różnicy ich promieni, a mniejsza od sumy promieni, to okręgi te przecinają się.
Zauważmy, że prawdziwe są również twierdzenia odwrotne do każdego z powyższych twierdzeń.
Moglibyśmy zapisać każde z powyższych twierdzeń bez konieczności wykorzystywania pojęcia wartości bezwzględnej, o ile wprowadzimy porządek w długościach promieni. Sformułujemy wówczas powyższe twierdzenia jako odpowiednie warunki równoważne.
Dane są okręgi o środkach w punktach i i promieniach i , gdzie . Wtedy:
okręgi i są styczne zewnętrznie wtedy i tylko wtedy, gdy ;
okręgi i , o różnych promieniach, są styczne wewnętrznie wtedy i tylko wtedy, gdy ;
okręgi i przecinają się w dwóch punktach wtedy i tylko wtedy, gdy ;
każdy z okręgów i leży na zewnątrz drugiego wtedy i tylko wtedy, gdy ;
okrąg leży wewnątrz okręgu wtedy i tylko wtedy, gdy .
Okazuje się, że już w czasach starożytnych badano zagadnienie szczególnego położenia większej liczby okręgów. Już w wieku Apoloniusz z Pergi badał istnienie okręgu stycznego do trzech danych okręgów. Co prawda, rozwiązanie postawionego przez Apoloniusza problemu zawdzięczamy Kartezjuszowi, ale to Frederick Soddy, laureat Nagrody Nobla w dziedzinie chemii, zasłużył na to, by jego imieniem nazwać okręgi styczne do trzech danychokręgi styczne do trzech danych, wzajemnie stycznych okręgów. A swoją drogą ciekawe, jak bez znajomości dokonań Kartezjusza radzili sobie budowniczowie gotyckich zabytków, w szczególności twórcy maswerkówmaswerków.
Dwa okręgi o środkach w punktach i i promieniach i przecinają się w punktach i .
Pokażemy, że ich wspólna cięciwa jest prostopadła do odcinka łączącego środki okręgów.
Rozwiązanie:
Zauważmy, że trójkąty i są przystające na mocy cechy .

Zauważmy, że wówczas kąty i są równe, zatem jest dwusieczną w trójkącie równoramiennym i tym samym zawiera wysokość tego trójkąta. Stąd teza.
Dany jest okrąg o środku i promieniu .
Wyznaczymy liczbę okręgów o promieniu potrzebnych do otoczenia danego okręgu, tj. stycznych zewnętrznie do danego okręgu i takich, że każde dwa sąsiednie są styczne zewnętrznie, jak na rysunku.
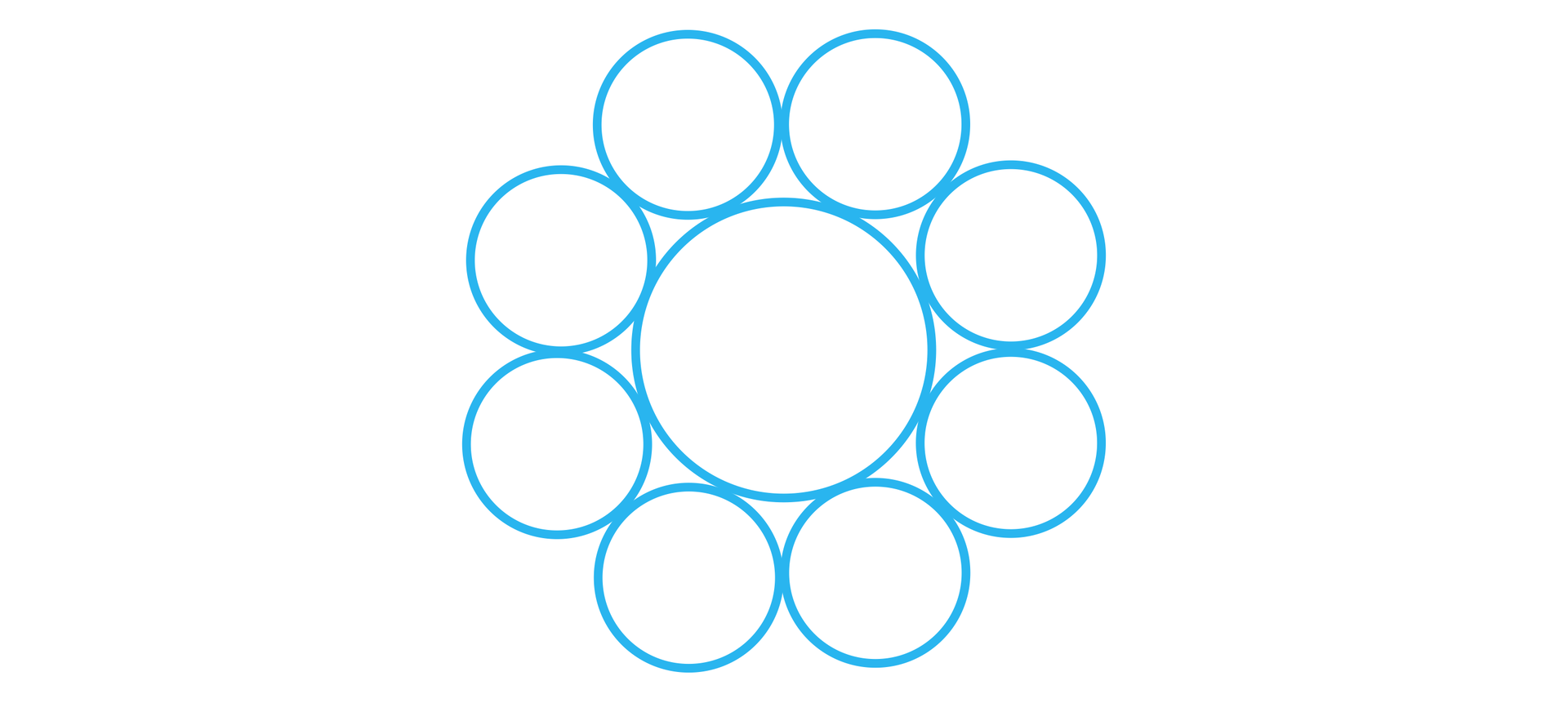
Rozwiązanie:
Rozważmy dany okrąg o środku i promieniu i dwa sąsiednie okręgi o zadanej własności, o środkach w punktach odpowiednio i , jak na rysunku.

Zauważmy, że wówczas trójkąt jest trójkątem równobocznym.
Zatem .
Oznacza to, że do otoczenia danego okręgu powinniśmy sześciokrotnie odmierzyć taki sam kąt i dorysować okręgi, z których dwa się „powtórzą”.
Stąd liczba okręgów niezbędnych do otoczenia jest równa .
Dane są dwa współśrodkowe okręgi o promieniach odpowiednio i .
Wyznaczymy promień okręgu, który jest styczny do danych okręgów.
Rozwiązanie:
Model, który narzuca się przy rozwiązaniu naszego problemu, jest przedstawiony na poniższym rysunku.
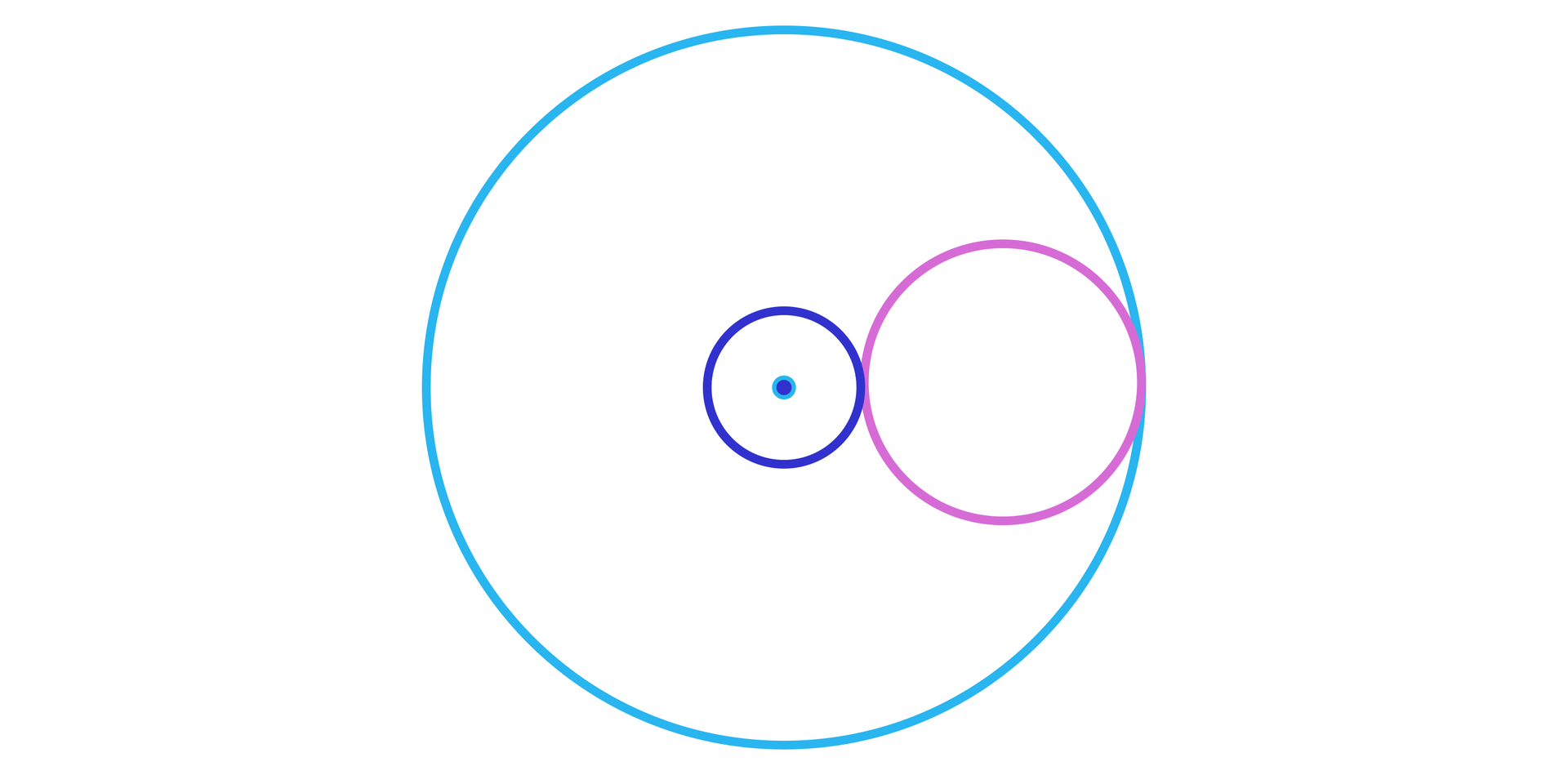
Jeśli przez oznaczymy szukany promień, to mamy spełnioną równość: .
Stąd .
Mniej oczywistym jest model, w którym szukany okrąg jest styczny w sposób przedstawiony na poniższym rysunku.
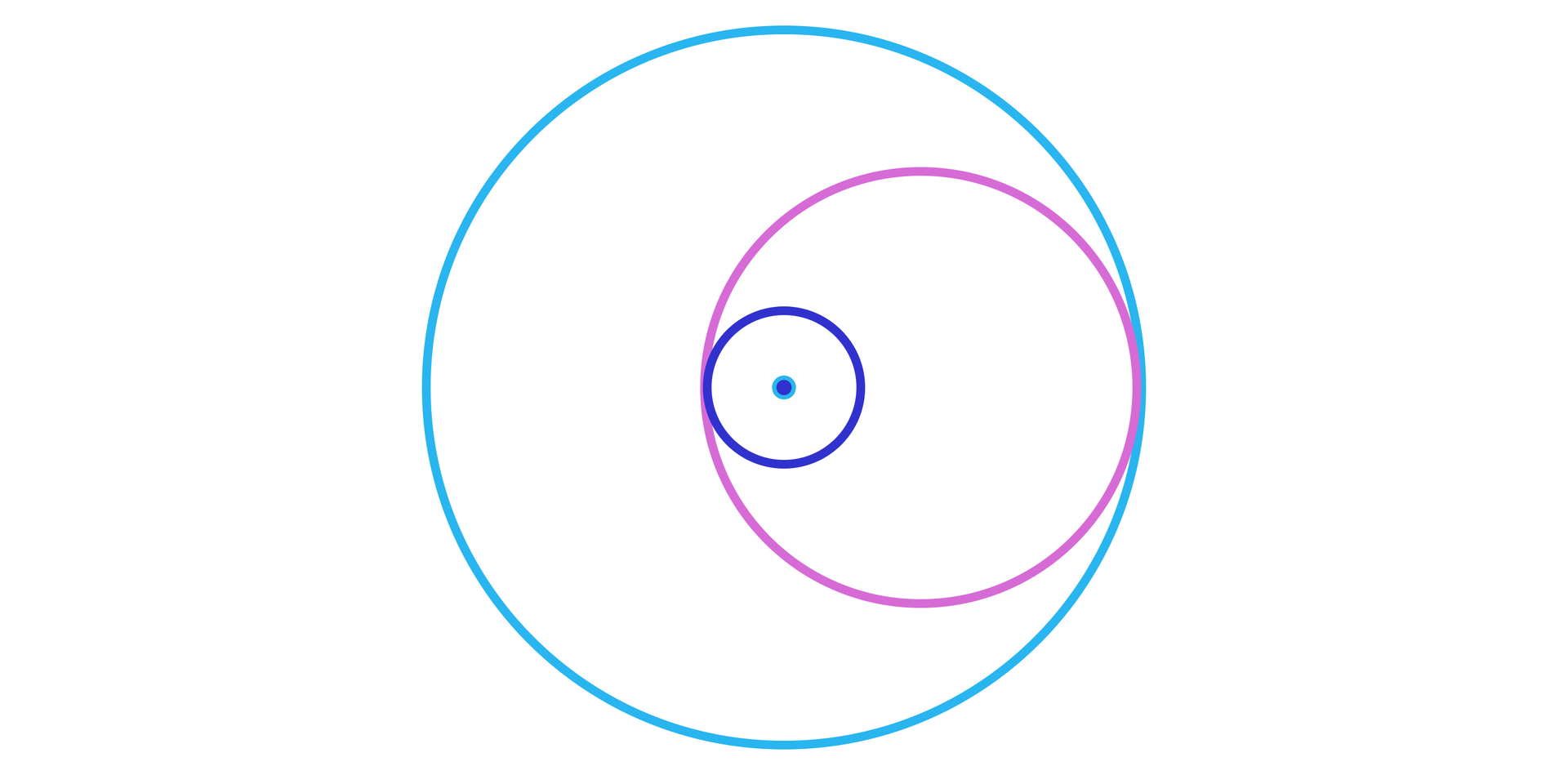
Wówczas otrzymujemy: .
Stąd .
Słownik
geometryczny wzór architektoniczny o charakterze dekoracyjnym, wykuty z kamienia lub zrobiony z cegieł, używany do wypełnienia górnej części gotyckiego okna, witrażu, rozety itp.
dwa okręgi styczne do danych trzech okręgów są nazywane okręgami Soddy’ego