1. $\frac{W_1\left(x\right)}{W_2\left(x\right)}>0 \iff W_1\left(x\right)·W_2\left(x\right)>0 \wedge W_2\left(x\right)\ne 0$,

2. $\frac{W_1\left(x\right)}{W_2\left(x\right)}<0 \iff W_1\left(x\right)·W_2\left(x\right)<0 \wedge W_2\left(x\right)\ne 0$,

3. $\frac{W_1\left(x\right)}{W_2\left(x\right)}\ge 0 \iff W_1\left(x\right)·W_2\left(x\right)\ge 0 \wedge W_2\left(x\right)\ne 0$,

4. $\frac{W_1\left(x\right)}{W_2\left(x\right)}\le 0 \iff W_1\left(x\right)·W_2\left(x\right)\le 0 \wedge W_2\left(x\right)\ne 0$.

Rozwiążmy nierówność $\frac{x}{x^2-3x}-\frac{3x-9}{x^2-9}<0$.

Rozwiązanie

Podajmy konieczne założenia

$x^2-3x\ne 0$, $x^2-9\ne 0$

$x\left(x-3\right)\ne 0$, $\left(x-3\right)\left(x+3\right)\ne 0$

$x\ne 0$, $x\ne 3$, $x\ne -3$

$D=\mathrm{ℝ}\setminus \left\{-3;0;3\right\}$.

Zapisujemy  mianowniki w   postaci iloczynowej

$\frac{x}{x\left(x-3\right)}-\frac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}<0$.

Skracamy ułamki

$\frac{1}{x-3}-\frac{3}{x+3}<0$.

Pomnożymy obie strony nierówności przez ${\left(x-3\right)}^2·{\left(x+3\right)}^2$, ponieważ ${\left(x-3\right)}^2·{\left(x+3\right)}^2>0$ dla $x\in D=\mathrm{ℝ}\setminus \left\{-3;0;3\right\}$.

Zauważmy, że nie możemy mnożyć obustronnie przez wyrażenie $\left(x-3\right)·\left(x+3\right)$, bo dane wyrażenie przyjmuje w dziedzinie nierówności wymiernejdziedzina nierówności wymiernejdziedzinie nierówności wymiernej $D=\mathrm{ℝ}\setminus \left\{-3;0;3\right\}$ zarówno wartości ujemne, jak też dodatnie.

$\frac{1}{x-3}-\frac{3}{x+3}<0|\cdot {\left(x-3\right)}^2\cdot {\left(x+3\right)}^2$ dla $x\in D=\mathrm{ℝ}\setminus \left\{-3;0;3\right\}$.

$\left(x-3\right){\left(x+3\right)}^2-3{\left(x-3\right)}^2\left(x+3\right)<0$.

Wyłączamy wspólny czynnik przed nawias $\left(x-3\right)\left(x+3\right)\left[x+3-3\left(x-3\right)\right]<0$.

Stąd

$\left(x-3\right)\left(x+3\right)\left(x+3-3x+9\right)<0$,

$\left(x-3\right)\left(x+3\right)\left(-2x+12\right)<0$,

$-2\left(x-3\right)\left(x+3\right)\left(x-6\right)<0$.

Wielomian $W\left(x\right)=-2\left(x-3\right)\left(x+3\right)\left(x-6\right)$ ma trzy pierwiastkipierwiastek wielomianupierwiastki jednokrotne: $\left(-3\right)$, $3$ oraz $6$.

Teraz przystępujemy do utworzenia „siatki znaków”.

RqY6cf9FytIuU

Tabela przedstawia analizę znaków nierówności $-2\left(x-3\right)\left(x+3\right)\left(x-6\right)<0$. Rozpatrujemy dziewięć kolumn z następującymi nagłówkami: 1. $\left(-\infty ,-3\right)$, 2. minus 3, 3. $\left(-3,0\right)$, 4. zero, 5. $\left(0,3\right)$, 6. trzy, 7. $\left(3,6\right)$, 8. sześć, 9. $\left(6,\infty \right)$. W pierwszym wierszu rozpatrujemy dwumian liniowy x plus trzy. Zapisujemy odpowiednie symbole pod kolejnymi nagłówkami kolumn: Pod pierwszym nagłówkiem minus, pod drugim 0, pod trzecim plus, pod czwartym nic, pod piątym plus, pod szóstym nic, pod siódmym plus, pod ósmym nic i pod dziewiątym plus. W drugim wierszu rozpatrujemy dwumian liniowy x minus 3. Zapisujemy odpowiednie symbole pod kolejnymi nagłówkami kolumn: Pod pierwszym nagłówkiem minus, pod drugim nic, pod trzecim minus, pod czwartym nic, pod piątym minus, pod szóstym zero, pod siódmym plus, pod ósmym nic i pod dziewiątym plus. W trzecim wierszu rozpatrujemy dwumian liniowy x minus 6. Zapisujemy odpowiednie symbole pod kolejnymi nagłówkami kolumn: Pod pierwszym nagłówkiem minus, pod drugim nic, pod trzecim minus, pod czwartym nic, pod piątym minus, pod szóstym nic, pod siódmym minus, pod ósmym zero i pod dziewiątym plus. W czwartym wierszu rozpatrujemy minus dwa. Zapisujemy odpowiednie symbole pod kolejnymi nagłówkami kolumn: Pod pierwszym nagłówkiem minus, pod drugim nic, pod trzecim minus, pod czwartym nic, pod piątym minus, pod szóstym nic, pod siódmym minus, pod ósmym nic i pod dziewiątym minus. W ostatnim wierszu rozpatrujemy cały wielomian $W\left(x\right)=-2\left(x-3\right)\left(x+3\right)\left(x-6\right)$. Pod pierwszym nagłówkiem mamy plus, pod drugim x, pod trzecim minus, pod czwartym x, pod piątym minus, pod szóstym x, pod siódmym plus, pod ósmym zero, pod dziewiątym minus.

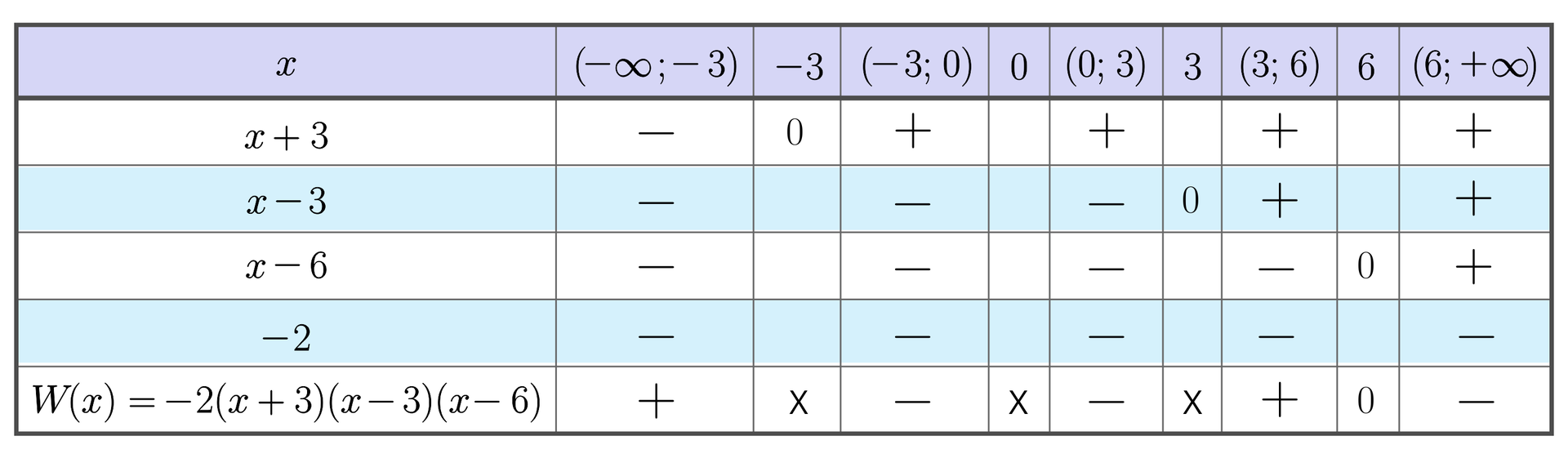
Z tabeli odczytujemy rozwiązanie nierówności.

Odpowiedź: Zbiorem rozwiązań nierówności jest zbiór $\left(-3;0\right)\cup \left(0;3\right)\cup \left(6;+\infty \right)$.

Rozwiążmy nierówność $\frac{x-1}{x^2-4x-5}-\frac{x+3}{x+1}\ge \frac{2}{x-5}$.

Rozwiązanie

Podajmy konieczne założenia

$x^2-4x-5\ne 0$, $x+1\ne 0$, $x-5\ne 0$

$\left(x+1\right)\left(x-5\right)\ne 0$, $x\ne -1$, $x\ne 5$

$x\ne -1$, $x\ne 5$

$D=\mathrm{ℝ}\setminus \left\{-1;5\right\}$.

Zapisujemy mianowniki w postaci iloczynowej

$\frac{x-1}{\left(x+1\right)\left(x-5\right)}-\frac{x+3}{x+1}\ge \frac{2}{x-5}$.

Przenosimy wyrażenia na jedną stronę nierówności

$\frac{x-1}{\left(x+1\right)\left(x-5\right)}-\frac{x+3}{x+1}-\frac{2}{x-5}\ge 0$.

Sprowadzamy ułamki do wspólnego mianownika

$\frac{x-1}{\left(x+1\right)\left(x-5\right)}-\frac{\left(x+3\right)\left(x-5\right)}{\left(x+1\right)\left(x-5\right)}-\frac{2\left(x+1\right)}{\left(x+1\right)\left(x-5\right)}\ge 0$,

$\frac{x-1-\left(x+3\right)\left(x-5\right)-2\left(x+1\right)}{\left(x+1\right)\left(x-5\right)}\ge 0$,

$\frac{x-1-\left(x^2-2x-15\right)-2x-2}{\left(x+1\right)\left(x-5\right)}\ge 0$,

$\frac{x-1-x^2+2x+15-2x-2}{\left(x+1\right)\left(x-5\right)}\ge 0$.

Zapisujemy nierówność wielomianową w postaci iloczynowej

$-\left(x-4\right)\left(x+3\right)\left(x+1\right)\left(x-5\right)\ge 0$.

Wielomian $W\left(x\right)=-\left(x-4\right)\left(x+3\right)\left(x+1\right)\left(x-5\right)$ ma cztery pierwiastkipierwiastek wielomianupierwiastki jednokrotne: $\left(-3\right)$, $\left(-1\right)$, $4$, $5$.

Uwzględniając dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej $D=\mathrm{ℝ}\setminus \left\{-1;5\right\}$ rozwiązaniem nierówności jest zbiór $\left.⟨-3;-1\right)\cup \left.⟨4;5\right)$

R1Ww7RVWyolx2

Na ilustracji przedstawiono wykres funkcji wielomianowej, biegnącej w następujący sposób. Od minus nieskończoności biegnie pod osią $X$, a następnie w zamalowanym punkcie -3 przebija nad oś. Biegnie w górę, po czym odbija w dół i w niezamalowanym punkcie -1 przebija pod oś $X$, biegnie w dół, następnie odbija w górę i w zamalowanym punkcie 4 przebija nad oś. Biegnie w górę, odbija w dół i przebija pod oś $X$ w niezamalowanym punkcie pięć. Pod osią biegnie do plus nieskończoności.

Odpowiedź: Rozwiązanie nierówności:  $x\in \left.⟨-3;-1\right)\cup \left.⟨4;5\right)$.

Obliczmy największą liczbę całkowitą spełniającą nierówność

$\frac{2x+3}{x^2-6x}-\frac{2}{6+x}>\frac{3x}{x^2-36}$.

Zakodujmy kolejno cyfrę setek, dziesiątek i jedności sześcianu otrzymanego wyniku.

Rozwiązanie

Podajmy konieczne założenia

$x^2-6x\ne 0$, $6+x\ne 0$, $x^2-36\ne 0$

$x\left(x-6\right)\ne 0$, $6+x\ne 0$, $\left(x-6\right)\left(x+6\right)\ne 0$

$x\ne 0$, $x\ne 6$, $x\ne -6$

$D=\mathrm{ℝ}\setminus \left\{-6;0;6\right\}$.

Przenosimy wyrażenia na jedną stronę nierówności:

$\frac{2x+3}{x^2-6x}-\frac{2}{6+x}-\frac{3x}{x^2-36}>0$.

Zapisujemy mianowniki w  postaci iloczynowej

$\frac{2x+3}{x\left(x-6\right)}-\frac{2}{6+x}-\frac{3x}{\left(x-6\right){\displaystyle \left(x+6\right)}}>0$.

Sprowadzamy ułamki do wspólnego mianownika

$\frac{\left(2x+3\right)\left(x+6\right)}{x\left(x-6\right)\left(x+6\right)}-\frac{2x\left(x-6\right)}{x\left(x-6\right)\left(x+6\right)}-\frac{3x^2}{x\left(x-6\right)\left(x+6\right)}>0$,

$\frac{2x^2+15x+18-2x^2+12x-3x^2}{x\left(x-6\right)\left(x+6\right)}>0$,

$\frac{-3x^2+27x+18}{x\left(x-6\right)\left(x+6\right)}>0$.

Zapisujemy nierówność wielomianową w postaci iloczynowej

$x\left(-3x^2+27x+18\right)\left(x-6\right)\left(x+6\right)>0$,

$-3x\left(x-\frac{9+\sqrt{105}}{2}\right)\left(x-\frac{9-\sqrt{105}}{2}\right)\left(x-6\right)\left(x+6\right)>0$.

Wielomian $P\left(x\right)=-3x\left(x-\frac{9+\sqrt{105}}{2}\right)\left(x-\frac{9-\sqrt{105}}{2}\right)\left(x-6\right)\left(x+6\right)$ ma pięć pierwiastków jednokrotnych: $\left(-6\right)$, $\frac{9-\sqrt{105}}{2}$, $0$, $6$, $\frac{9+\sqrt{105}}{2}$.

Uwzględniając dziedzinę nierówności wymiernej $D=\mathrm{ℝ}\setminus \left\{-6;0;6\right\}$ rozwiązaniem nierówności jest zbiór $x\in \left(-\infty ;-6\right)\cup \left(\frac{9-\sqrt{105}}{2};0\right)\cup \left(6;\frac{9+\sqrt{105}}{2}\right)$.

R1kS4jAlnMSXp

Na ilustracji przedstawiono wykres funkcji wielomianowej, biegnącej w następujący sposób. Od minus nieskończoności biegnie nad osią $X$, po czym w niezamalowanym punkcie minus 6 przebija pod oś $X$. Biegnie w dół, obija w górę i przebija nad oś $X$ w zamalowanym punkcie $\frac{9-\sqrt{105}}{2}$. Biegnie w górę i odbija w dół, tworząc ostry wierzchołek i w niezamalowanym punkcie 0 przebija pod oś. Biegnie w dół, odbija w górę i w niezamalowanym punkcie 6 przebija nad oś. Następnie biegnie w górę, odbija w dół i w zamalowanym punkcie $\frac{9+\sqrt{105}}{2}$ przebija pod oś $X$ i biegnie do plus nieskończoności.

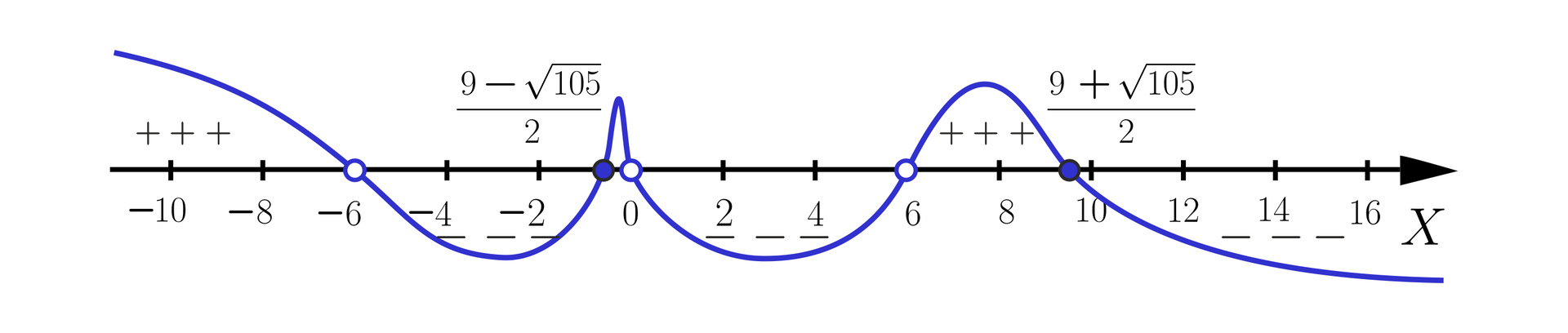
Zatem największą liczbę całkowitą spełniającą nierówność jest liczba $9$. Wówczas $9^3=729$.

Odpowiedź: $729$.

Rozwiążmy nierówność $\left|\frac{3}{2x-1}-\frac{x}{x-2}\right|\le 1$.

Rozwiązanie

$D=\mathrm{ℝ}\setminus \left\{\frac{1}{2};2\right\}$.

Rozwiążmy nierówności:$\frac{3}{2x-1}-\frac{x}{x-2}\ge -1\wedge \frac{{\displaystyle 3}}{{\displaystyle 2x-1}}-\frac{{\displaystyle x}}{{\displaystyle x-2}}\le 1$.

Przenieśmy wszystkich wyrażenia na jedną stronę $\frac{3}{2x-1}-\frac{x}{x-2}+1\ge 0\wedge \frac{{\displaystyle 3}}{{\displaystyle 2x-1}}-\frac{{\displaystyle x}}{{\displaystyle x-2}}-1\le 0$.

Sprowadźmy ułamki algebraiczne do wspólnego mianownika

$\frac{3\left(x-2\right)}{\left(2x-1\right)\left(x-2\right)}-\frac{x\left(2x-1\right)}{\left(2x-1\right)\left(x-2\right)}+\frac{\left(2x-1\right)\left(x-2\right)}{\left(2x-1\right)\left(x-2\right)}\ge 0\wedge \frac{{\displaystyle 3\left(x-2\right)}}{{\displaystyle \left(2x-1\right)\left(x-2\right)}}-\frac{{\displaystyle x\left(2x-1\right)}}{{\displaystyle \left(2x-1\right)\left(x-2\right)}}-\frac{\left(2x-1\right)\left(x-2\right)}{\left(2x-1\right)\left(x-2\right)}\le 0$

$\frac{3x-6}{\left(2x-1\right)\left(x-2\right)}-\frac{2x^2-x}{\left(2x-1\right)\left(x-2\right)}+\frac{2x^2-4x-x+2}{\left(2x-1\right)\left(x-2\right)}\ge 0\wedge \frac{{\displaystyle 3x-6}}{{\displaystyle \left(2x-1\right)\left(x-2\right)}}-\frac{{\displaystyle 2x^2-x}}{{\displaystyle \left(2x-1\right)\left(x-2\right)}}-\frac{2x^2-4x-x+2}{\left(2x-1\right)\left(x-2\right)}\le 0$

$\frac{3x-6-2x^2+x+2x^2-5x+2}{\left(2x-1\right)\left(x-2\right)}\ge 0\wedge \frac{{\displaystyle 3x-6-2x^2+x-2x^2+5x-2}}{{\displaystyle \left(2x-1\right)\left(x-2\right)}}\le 0$

$\frac{-x-4}{\left(2x-1\right)\left(x-2\right)}\ge 0\wedge \frac{{\displaystyle -4x^2+9x-8}}{{\displaystyle \left(2x-1\right)\left(x-2\right)}}\le 0$.

Zapiszmy nierówności w postaci równoważnych nierówności iloczynowych

$\left(-x-4\right)\left(2x-1\right)\left(x-2\right)\ge 0\wedge \left(-4x^2+9x-8\right)\left(2x-1\right)\left(x-2\right)\le 0$,

$-2\left(x+4\right)\left(x-\frac{1}{2}\right)\left(x-2\right)\ge 0\wedge 2\left(-4x^2+9x-8\right)\left(x-\frac{1}{2}\right)\left(x-2\right)\le 0$.

Wielomian $R_1\left(x\right)=-2\left(x+4\right)\left(x-\frac{1}{2}\right)\left(x-2\right)$ ma trzy pierwiastki jednokrotne: $\left(-4\right)$,$\frac{1}{2}$,$2$.

Uwzględniając dziedzinę $D=\mathrm{ℝ}\setminus \left\{\frac{1}{2};2\right\}$ sporządzamy wykres funkcji $R_1$.

R1XHuykbqxfLR

Na ilustracji przedstawiono wykres funkcji wielomianowej, biegnącej w następujący sposób. Od minus nieskończoności biegnie nad osią $X$, po czym w zamalowanym punkcie cztery przebija pod oś. Biegnie w dół, odbija w górę i w niezamalowanym punkcie $\frac{1}{2}$ przebija nad oś. Następnie biegnie w górę, odbija w dół i w niezamalowanym punkcie 2 przebija pod oś i biegnie do plus nieskończoności.

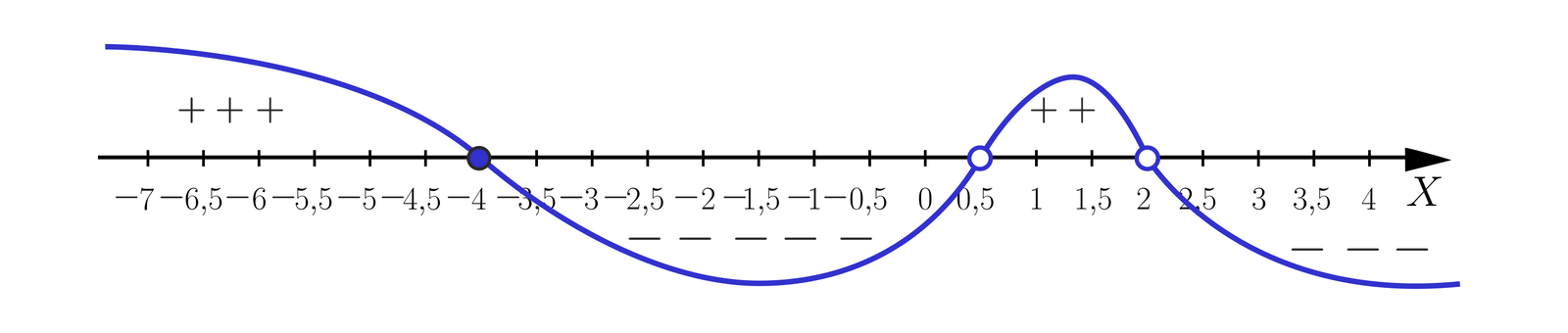
Rozwiązaniem pierwszej nierówności wielomianowej, gdzie $x\in D=\mathrm{ℝ}\setminus \left\{\frac{1}{2};2\right\}$ jest zbiór $\left(-\infty ;- 4\right.⟩\cup \left(\frac{1}{2};2\right)$.

Wielomian $R_2\left(x\right)=2\left(-4x^2+9x-8\right)\left(x-\frac{1}{2}\right)\left(x-2\right)$ ma dwa pierwiastki jednokrotne: $\frac{1}{2}$, $2$.

Uwzględniając dziedzię $D=\mathrm{ℝ}\setminus \left\{\frac{1}{2};2\right\}$ sporządzamy wykres wielomianu $R_2$.

R18mB261frkH4

Na ilustracji przedstawiono wykres funkcji wielomianowej, biegnącej w następujący sposób. Od minus nieskończoności, biegnie pod osią $X$, po czym w niezamalowanym punkcie pięć dziesiątych przebija nad oś $X$. Biegnie w górę, odbija w dół, przebija pod oś $X$ w niezamalowanym punkcie dwa i biegnie do plus nieskończoności.

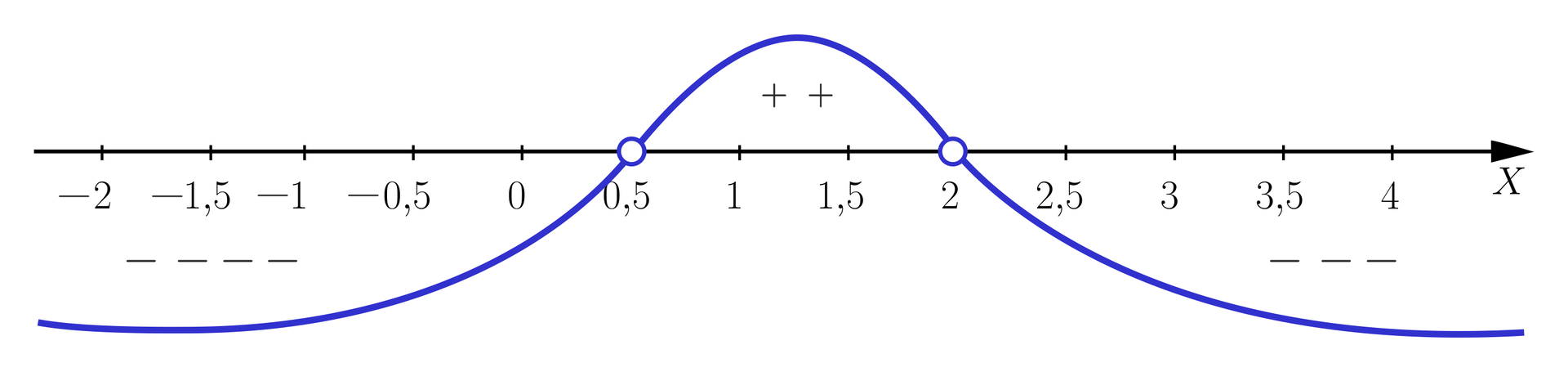
Rozwiązaniem drugiej nierówności wielomianowej, gdzie $x\in D=\mathrm{ℝ}\setminus \left\{\frac{1}{2};2\right\}$ jest zbiór $\left(-\infty ;\frac{1}{2}\right)\cup \left(2;+\infty \right)$.

Wyznaczamy iloczyn rozwiązań nierówności:

$\left[\left(-\infty ;- 4\right.⟩\cup \left(\frac{1}{2};2\right)\right]\cap \left[\left(-\infty ;\frac{1}{2}\right)\cup \left(2;+\infty \right)\right]=\left(-\infty ;- 4\right.⟩$.

Odpowiedź: Rozwiązaniem nierówności jest zbiór $\left(-\infty ;- 4\right.⟩$.

dziedziną nierówności wymiernej są wszystkie liczby rzeczywiste za wyjątkiem pierwiastków wielomianu $W_2\left(x\right)$ znajdującego się w mianowniku danego wyrażenia $\frac{W_1\left(x\right)}{W_2\left(x\right)}$

$D=\mathrm{ℝ} \setminus \left\{x: W_2\left(x\right)=0\right\}$

pierwiastkiem wielomianu $W\left(x\right)$ nazywamy liczbę rzeczywistą $a$, dla której $W\left(a\right)=0$