Przeczytaj

Jednokładność

Definicja: Jednokładność

R1ZQoghpHrj0L

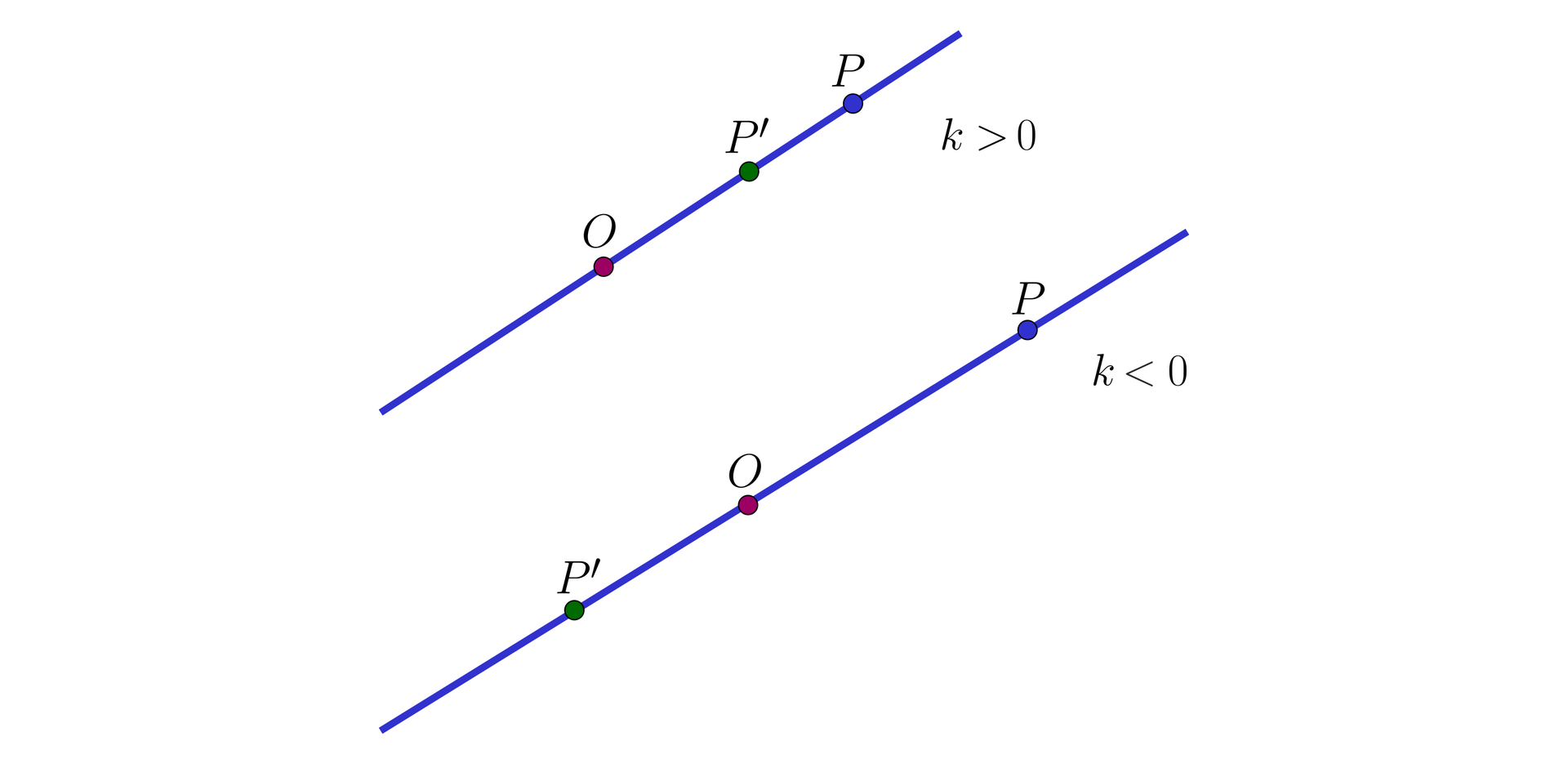
Na ilustracji przedstawiono dwie proste ukośne, równoległe do siebie. Nad pierwszą prostą, widoczna jest informacja k>0. Przebiega przez punkty, kolejno od dołu, O, P', P. Nad drugą prostą widoczna jest informacja k<0. Przebiega przez punkty, kolejno od dołu P', O, P.

Obrazem punktu $P$ w jednokładności o środku $O$ i skali $k$ jest punkt $P'$ taki, że punkty $O$ , $P$ , $P'$ są współliniowe i $|O P'| = |k| \cdot |O P|$ , przy czym jeśli $k > 0$ to punkty $P$ i $P'$ są po tej samej stronie środka $O$ , a jeśli $k < 0$ , to punkty $P$ i $P'$ są po różnych stronach środka $O$ .

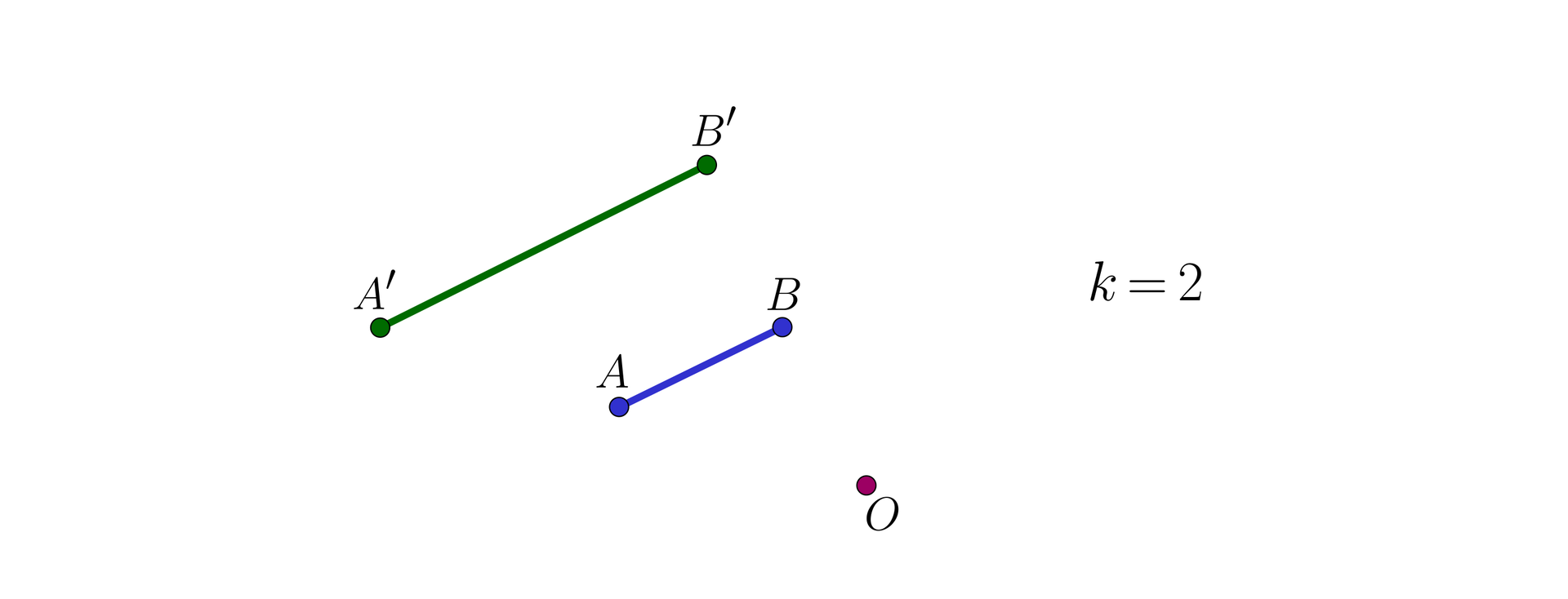
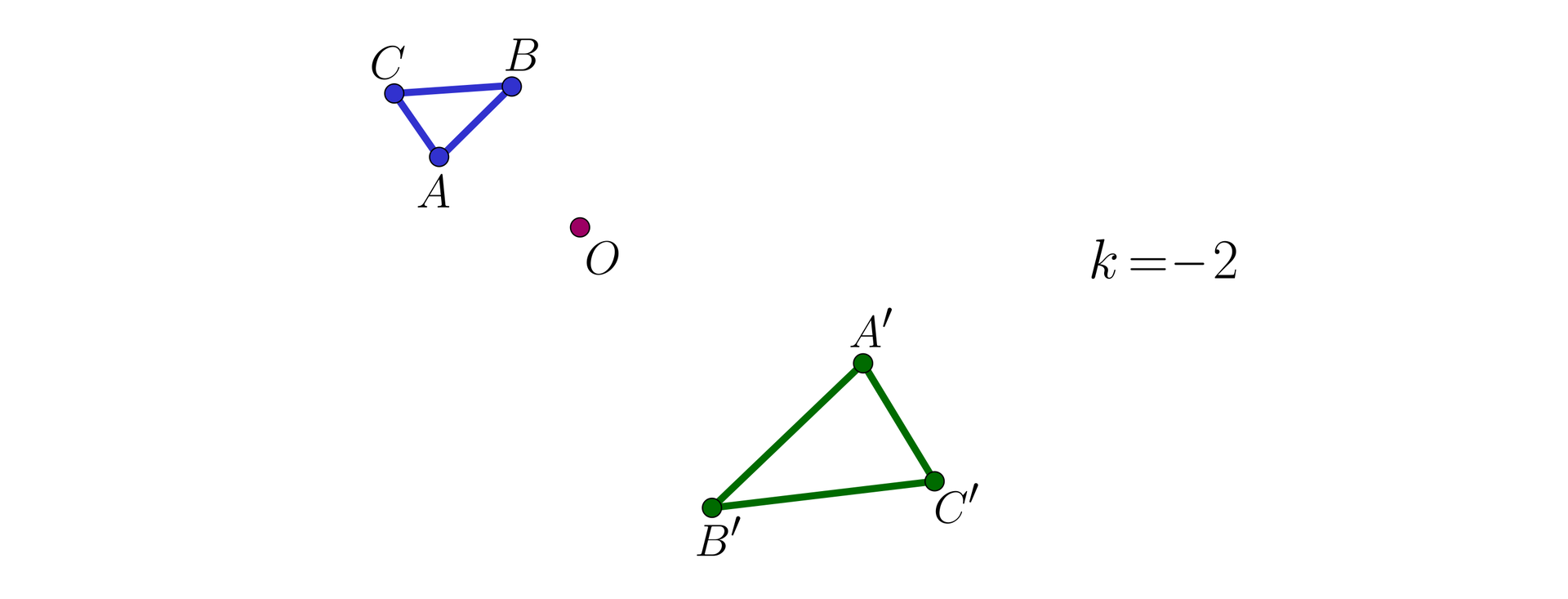
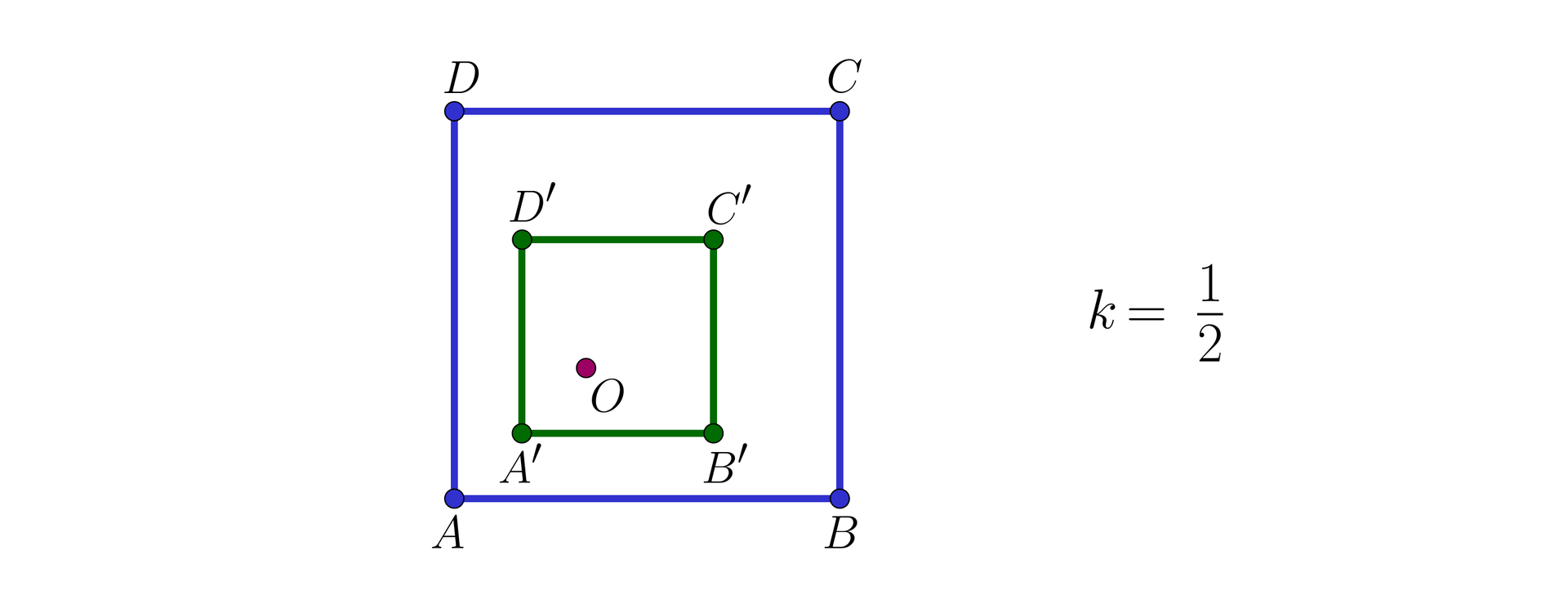
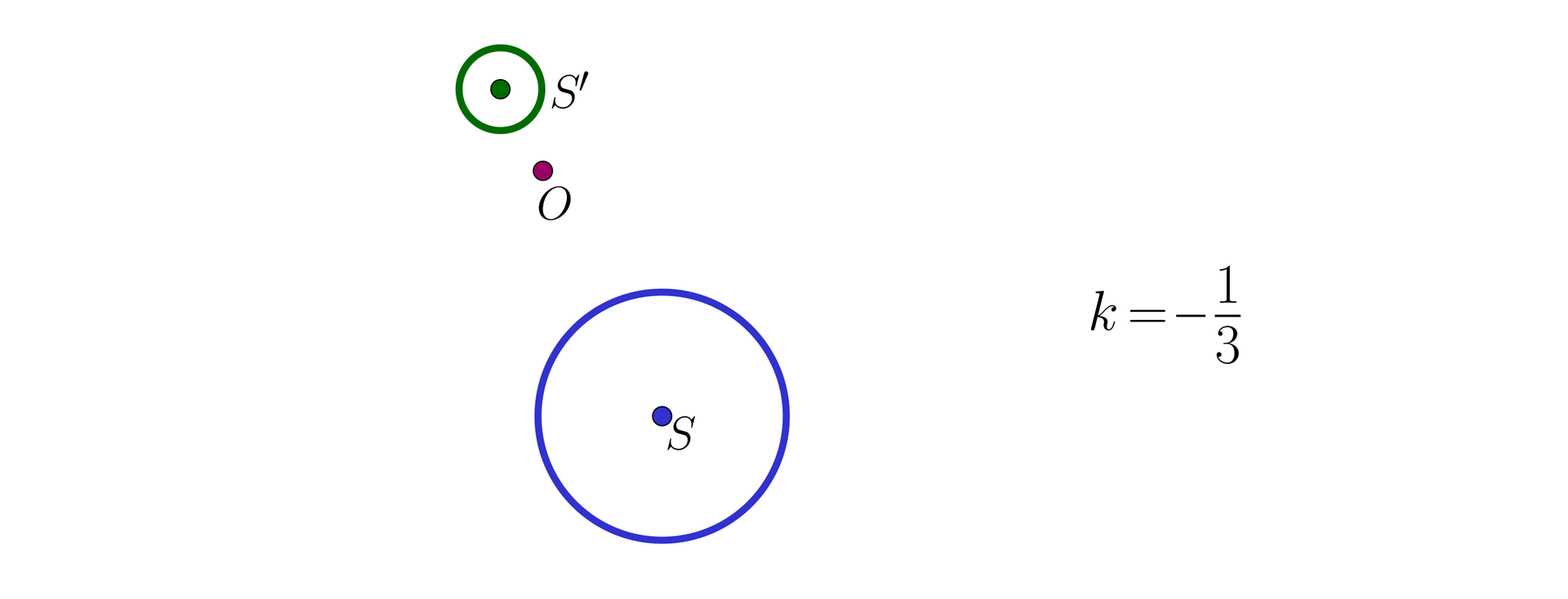
Na rysunkach podane są pary figur jednokładnychjednokładnośćjednokładnych.

RD5X7MmN6AZoj

Na ilustracji przedstawiono zielony odcinek A'B'. Pod odcinkiem A'B' znajduje się równoległy do niego, granatowy, krótszy odcinek AB. Poniżej, znajduje się punkt O, leżący w linii prostej z B' oraz AB. Po prawej stronie znajduje się informacja k=2.

RbrTvdhMuVI5z

Na ilustracji przedstawiono granatowy trójkąt ABC, znajdujący się w lewym górnym rogu. W prawym dolnym rogu, znajduje się większy, zielony trójkąt A'B'C'. Pomiędzy trójkątami znajduje się punkt O, leżący w linii prostej z wierzchołkiem A oraz A'. Po prawej stronie znajduje się informacja k=-2.

RcBp20UM7Uj7F

Na ilustracji przedstawiono granatowy kwadrat ABCD. Wewnątrz kwadratu ABCD, znajduje się mniejszy, zielony kwadrat A'B'C'D'. W dolnej części kwadratu A'B'C'D' znajduje się punkt O. Po prawej stronie znajduje się informacja k=12.

RlQIdm322KJrP

Na ilustracji znajduje się zielony okrąg o środku w punkcie S'. Poniżej, po prawej stronie znajduje się większy granatowy okrąg, o środku w punkcie S. Pomiędzy okręgami, bliżej zielonego, znajduje się punkt O. Po prawej stronie znajduje się informacja k=-13.

Własności jednokładności

Twierdzenie: Własności jednokładności

Jednokładność przekształca odcinek na równoległy do niego.
Obrazem odcinka $A B$ w jednokładności o środku $O$ i skali $k$ jest odcinek $A' B'$ taki, że $|A' B'| : |A B| = |k|$ , równoważnie $|A' B'| = |k| \cdot |A B|$
Jednokładność przekształca kąt na kąt o tej samej mierze.

Dowód

Do dowodu własności $1 .$ – $3 .$ w przypadku, gdy $k > 0$ zastosujemy twierdzenie Talesa i twierdzenie odwrotne do twierdzenia Talesa.

Na rysunku przedstawiony jest trójkąt $A B C$ i jego obraz $A' B' C'$ w jednokładności o środku $O$ i skali $k > 0$ .

Rl7icIMeuMkVf

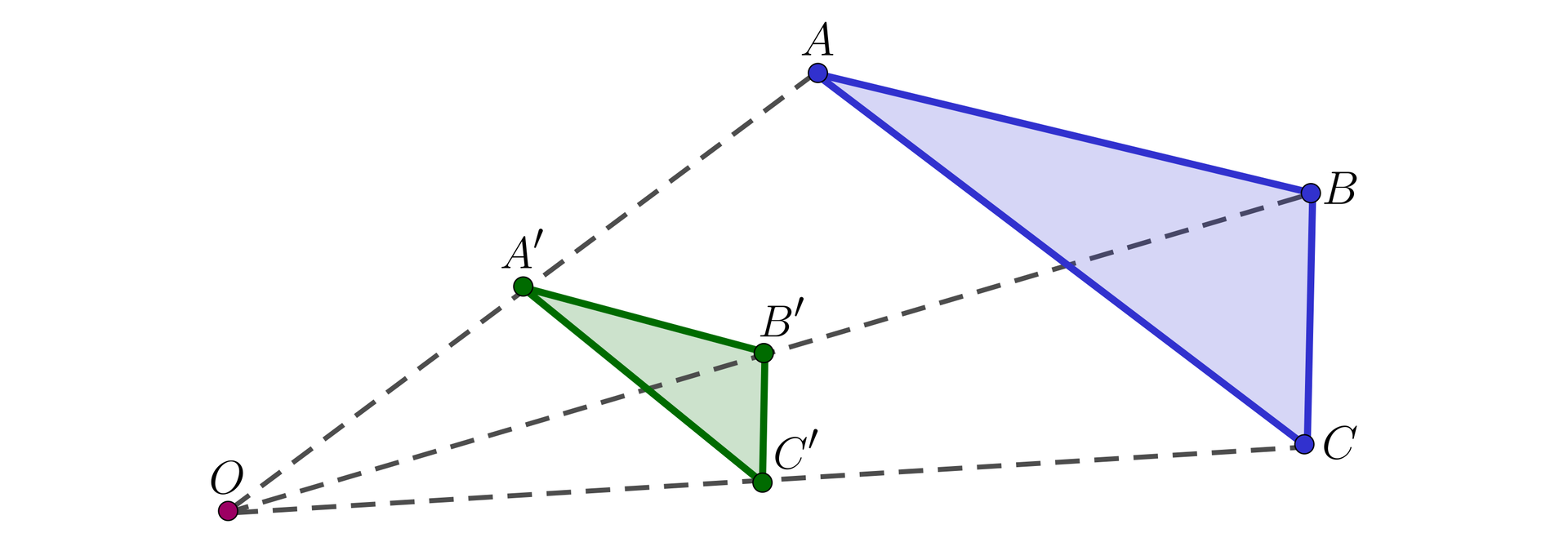
Na ilustracji przedstawiono, kolejno od lewej. Punkt O, zielony trójkąt A'B'C', oraz większy granatowy trójkąt ABC. Z punktu O, poprowadzono trzy linie proste, przerywane. Pierwsza linia łączy punkt O z wierzchołkiem A' oraz A. Druga linia łączy punkt O z wierzchołkiem B' oraz B. Trzecia linia łączy punkt O z wierzchołkiem C' oraz C.

Aby pokazać własność $1.$ zauważmy, że $\frac{|O A|}{|O A'|} = \frac{1}{k} = \frac{|O B|}{|O B'|}$ , więc na mocy odwrotnego twierdzenia Talesa $A' B' ∥ A B$ .
Z twierdzenia Talesa $\frac{|O A|}{|A B|} = \frac{|O A'|}{|A' B'|} = \frac{k |O A|}{|A' B'|}$ . Stąd $\frac{|A' B'|}{|A B|} = \frac{k |O A|}{|O A|} = k$ , co pokazuje własność $2$ .
Niech $α$ oznacza kąt $C A B$ , a $β$ – kąt $C' A' B'$ . Ponieważ z $1.$ wynika, że $A' B' ∥ A B$ oraz $A' C' ∥ A C$ , to kąty $O A' B'$ i $O A B$ są równe jako kąty odpowiadające. Również kąty $O A' C'$ i $O A C$ są odpowiadające, więc też równe. Stąd $α$ i $β$ są różnicami równych kątów, więc są równe.

W przypadku, gdy $k < 0$ stosujemy analogiczne rozumowanie z wykorzystaniem uogólnienia twierdzenia Talesa.

Przykład 1

Pokażemy, że wielokąty jednokładne mają odpowiednie kąty równe oraz równe stosunki odpowiednich boków.

Rozwiązanie

Rzeczywiście, z własności $3$ wynika, że kąty przekształcane są na kąty równej miary, a własność $2$ mówi, że stosunki odpowiednich boków są równe skali podobieństwa, więc też równe. Oznacza to, że każde dwa wielokąty jednokładne są też podobne.

Oczywiście twierdzenie odwrotne nie jest prawdziwe – wielokąty, które mają równe odpowiednie kąty oraz równe stosunki odpowiednich boków nie są jednokładne o ile odpowiednie boki nie są równoległe. Ta własność odróżnia pojęcie jednokładności i podobieństwa.

Własności relacji podobieństwa

Przypomnijmy własności relacji podobieństwa:

Każda figura jest podobna do siebie.
Relacja podobieństwa jest symetryczna, to znaczy, że jeśli jedna figura jest podobna do drugiej, to druga figura jest też podobna do pierwszej.
Relacja podobieństwa jest przechodnia, to znaczy, jeżeli jedna figura podobna jest do drugiej, a druga figura podobna do trzeciej, to również pierwsza figura podobna jest do trzeciej.

Skala podobieństwa i jej własności

Jeżeli figura $F_{1}$ jest podobna do figury $F_{2}$ , to stosunki odpowiednich odcinków $a_{1}$ i $a_{2}$ w tych figurach są równe. Stosunek $k = \frac{a_{1}}{a_{2}}$ nazywamy skalą podobieństwa figury $F_{1}$ do figury $F_{2}$
Jeśli jedna figura jest podobna do drugiej w skali k, to druga figura jest podobna do pierwszej w skali $\frac{1}{k}$ .
Jeśli jedna figura jest podobna do drugiej w skali $k$ , a druga figura jest podobna do trzeciej w skali $l$ , to pierwsza figura jest podobna do trzeciej w skali $k \cdot l$

Cechy podobieństwa trójkątów

W tej części przypomnimy cechy podobieństwa trójkątówcechy podobieństwa trójkątówcechy podobieństwa trójkątów. Zauważmy, że z własności jednokładności wynika, że jeśli dwa trójkąty są jednokładne, to boki jednego trójkąta są proporcjonalne do odpowiednich boków drugiego trójkąta (własność jednokładności) oraz miary kątów jednego trójkąta są równe miarom kątów drugiego trójkąta, jak również, dwa boki jednego trójkąta są proporcjonalne do odpowiednich dwóch boków drugiego trójkąta, a kąty między nimi zawarte mają równe miary.

Cechy podobieństwa trójkątów, to warunki konieczne i wystarczające na to, aby dwa trójkąty były podobne. Znane są trzy cechy podobieństwa trójkątów.

bok – bok – bokcecha podobieństwa bok – bok – bokbok – bok – bok (bbb) jeżeli boki jednego trójkąta są proporcjonalne do odpowiednich boków drugiego trójkąta, to trójkąty są podobne.
kąt – kąt– kątkąt – kąt– kąt (kkk): jeżeli miary dwóch kątów jednego trójkąta są równe miarom dwóch kątów drugiego trójkąta, to trójkąty są podobne.
bok – kąt – bokbok – kąt – bok (bkb): jeżeli dwa boki jednego trójkąta są proporcjonalne do odpowiednich dwóch boków drugiego trójkąta, a kąty między nimi zawarte mają równe miary, to trójkąty są podobne.

Przykład 2

Pokażemy, że jeśli punkty $D$ , $E$ leżą na bokach trójkąta $A B C$ tak, że odcinek $D E$ jest równoległy do boku $B C$ to trójkąty $A B C$ i $A D E$ są jednokładne.

Rozwiązanie

Popatrzmy na rysunek.

R193h2olIrIQf

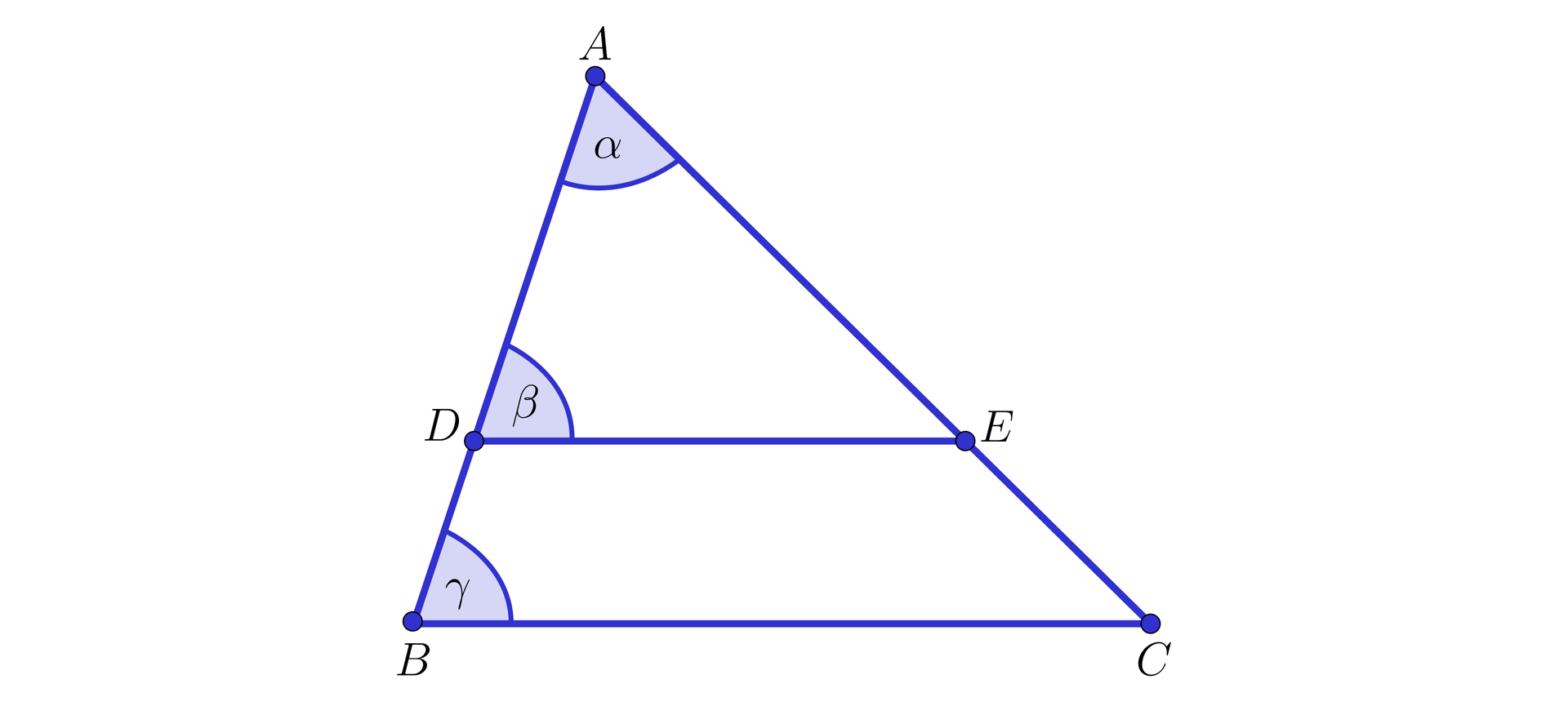
Na ilustracji przedstawiono trójkąt ABC. Na boku AB, zaznaczono punkt D. Na boku AC zaznaczono punkt E. Prosta DE jest równoległa do podstawy BC trójkąta. Wewnątrz trójkąta ADE, zaznaczono kąty. Przy wierzchołku A, zaznaczono kąt alfa. Przy wierzchołku D, zaznaczono kąt beta. Wewnątrz trójkąta ABC, przy wierzchołku B zaznaczono kąt gamma.

Trójkąty $A B C$ i $A D E$ mają wspólny kąt $α$ . Poza tym kąty $β$ i $γ$ są równe jako kąty odpowiadające.

Zatem spełniona jest cecha podobieństwa kkk, a stąd trójkąty $A B C$ i $A D E$ są podobne. Ponadto proste $D E$ i $B C$ , $A D$ i $A B$ oraz $A E$ i $A C$ są równoległe, więc rozważane trójkąty są też jednokładne.

Przykład 3

Na rysunku przedstawiono dwa trójkąty $A B C$ i $A D E$ , które mają wspólny wierzchołek $A$ , wierzchołki $A$ , $B$ , $D$ i wierzchołki $A$ , $C$ , $E$ są współliniowepunkty współliniowewspółliniowe oraz boki $B C$ i $D E$ są równoległe.

R1Wvi25AwWhJ4

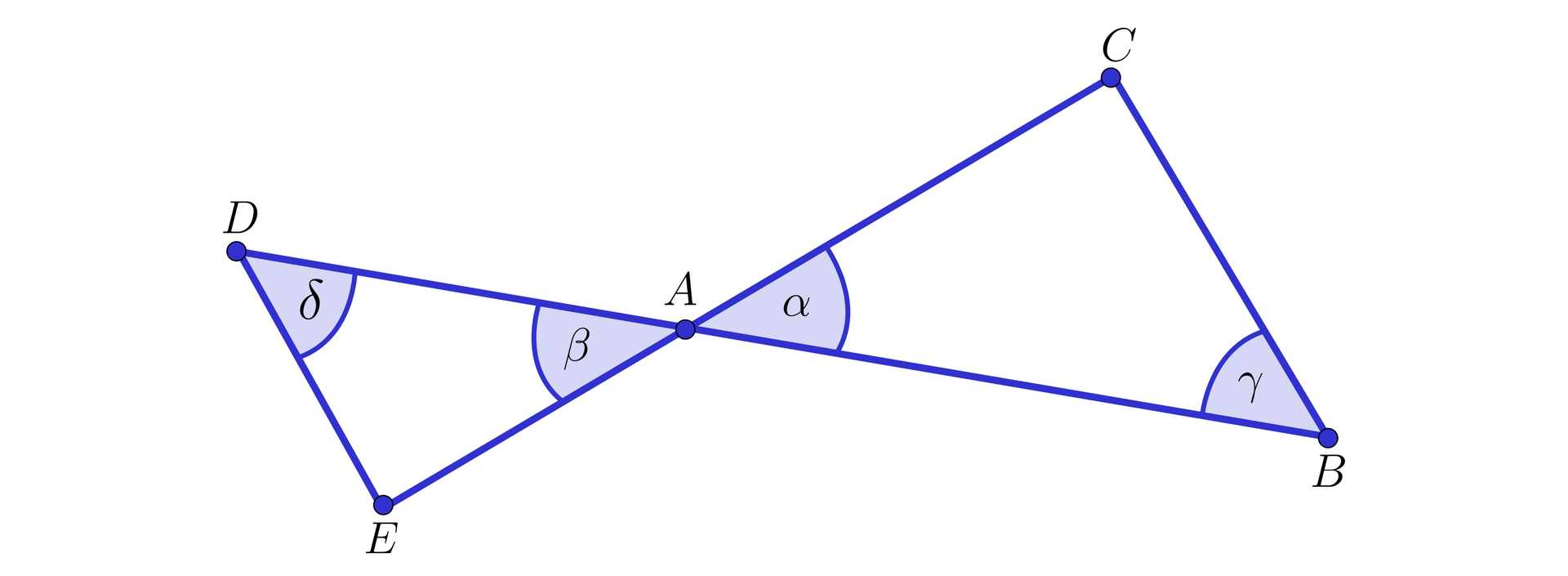
Na ilustracji przedstawiono dwa trójkąty ABC i ADE o wspólnym wierzchołku A. Wierzchołki E, A, C i wierzchołki A, C, E są współliniowe. Bok DE jest równoległy do boku BC. W trójkącie ABC zaznaczono kąty. Zaznaczono kąt alfa przy wierzchołku A, oraz kąt gamma przy wierzchołku B. W trójkącie ADE zaznaczono kąty. Kąt beta przy wierzchołku A, oraz kąt delta przy wierzchołku D.

Pokażemy, że trójkąty $A B C$ i $A D E$ są podobne.

Rozwiązanie

Skorzystamy z cechy podobieństwa kkk. Po pierwsze, kąty $α$ , $β$ są równe jako kąty wierzchołkowe. Po drugie, kąty $γ$ i $δ$ są równe jako kąty naprzemianległe.

Zatem spełniona jest cecha kkk, a stąd trójkąty $A B C$ i $A D E$ są podobne. Ponadto odpowiadające sobie boki w obu trójkątach są równoległe, co oznacza, że trójkąty są jednokładne

Twierdzenie Talesa wynika z podobieństwa trójkątów

Popatrzmy na dwie wersje twierdzenia Talesa.

Jeżeli proste $C A$ i $D B$ są równoległe, to prawdziwe są następujące równości:

R15kopoXKK5a9

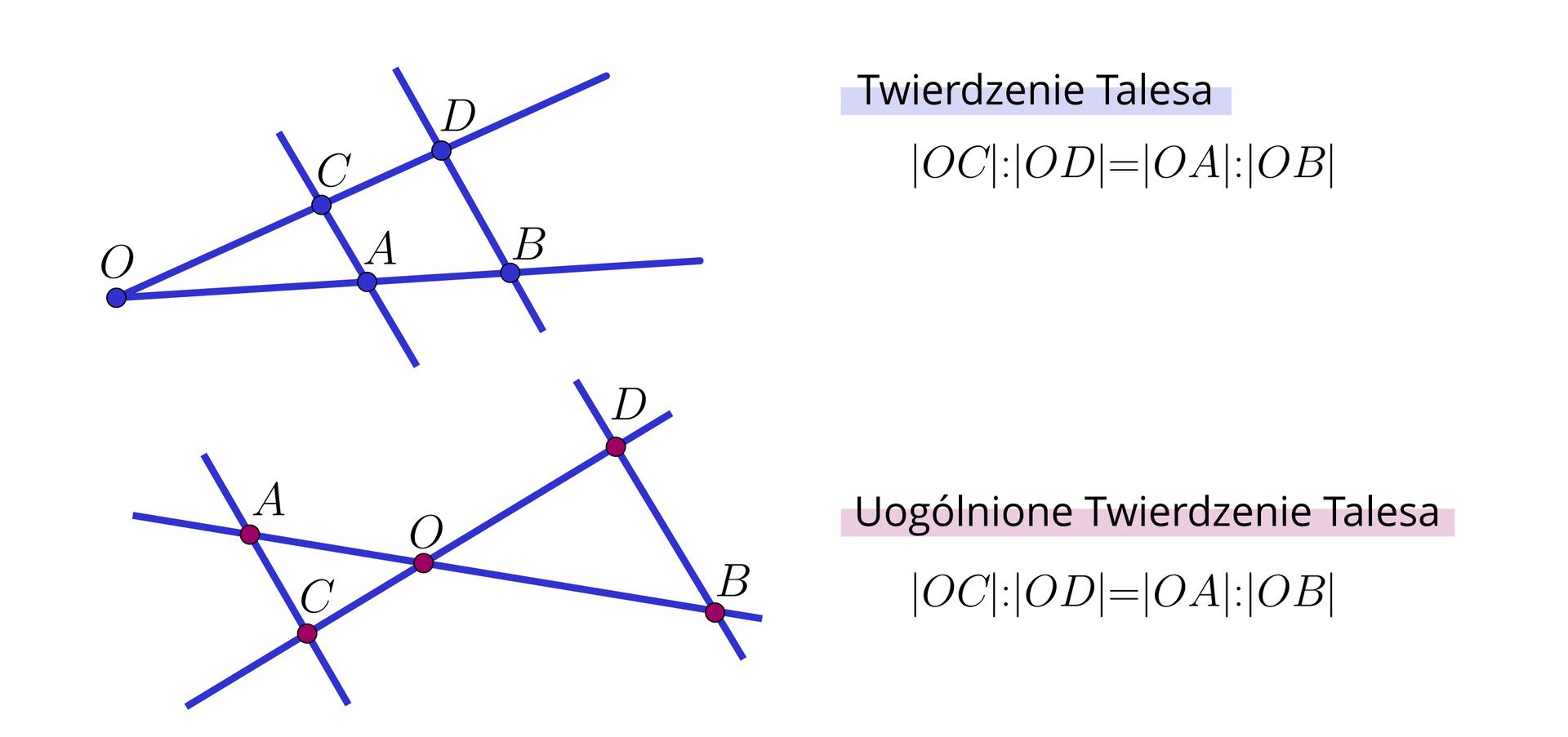
Na ilustracji przedstawiono dwa rysunki. Na rysunku pierwszym przedstawiono dwie proste równoległe AC i BD, przecinające ramiona kąta. Ramiona kąta, wychodzą z punktu O. Obok widoczny napis. Twierdzenie Talesa. OCw stosunku doOD=OAw stosunku doOB. Na rysunku drugim przedstawiono dwie proste równoległe, które przecinają ramiona kątów wierzchołkowych. Widoczne są dwa trójkąty ACO i BDO, o wspólnym wierzchołku O. Obok widoczny napis. Uogólnione Twierdzenie Talesa. OCw stosunku doOD=OAw stosunku do OB.

W przykładzie $2$ pokazaliśmy, że trójkąty $O A C$ i $O B D$ w wersji podstawowej twierdzenia Talesa są jednokładne. Natomiast w przykładzie $3$ pokazaliśmy, że trójkąty $O A C$ i $O B D$ w wersji uogólnionej twierdzenia Talesa są jednokładne.

W takim razie stosunki odpowiednich boków są równe, w szczególności $|O C| : |O D| = |O A| : |O B|$ w obu wersjach twierdzenia Talesa, co dowodzi tych twierdzeń. Stąd też mamy wniosek, że $|O C| : |O D| = |O A| : |O B| = |A C| : |B D|$ .

Twierdzenie odwrotne do twierdzenia Talesa wynika z podobieństwa trójkątów

Przy oznaczeniach z rysunku do Twierdzenia Talesa załóżmy, że $|O C| : |O D| = |O A| : |O B|$ . Ponieważ trójkąty $O A C$ i $O B D$ mają równe kąty przy wierzchołku $O$ , to z cechy kbk wynika ich podobieństwo. Stąd kąt przy wierzchołku $D$ jest równy kątowi przy wierzchołku $C$ , a to dowodzi równoległości odcinków $D B$ i $A C$ .

Przykład 4

Na przedstawionym rysunku odcinki $D E ∥ B C$ . Z twierdzenia Talesa wynika również, że

Trójkąty $A G E$ i $A F C$ są podobne
Trójkąty $A D G$ i $A B F$ są podobne
Trójkąty $A D E$ i $A B C$ są podobne

R110Z0Iscj6Rb

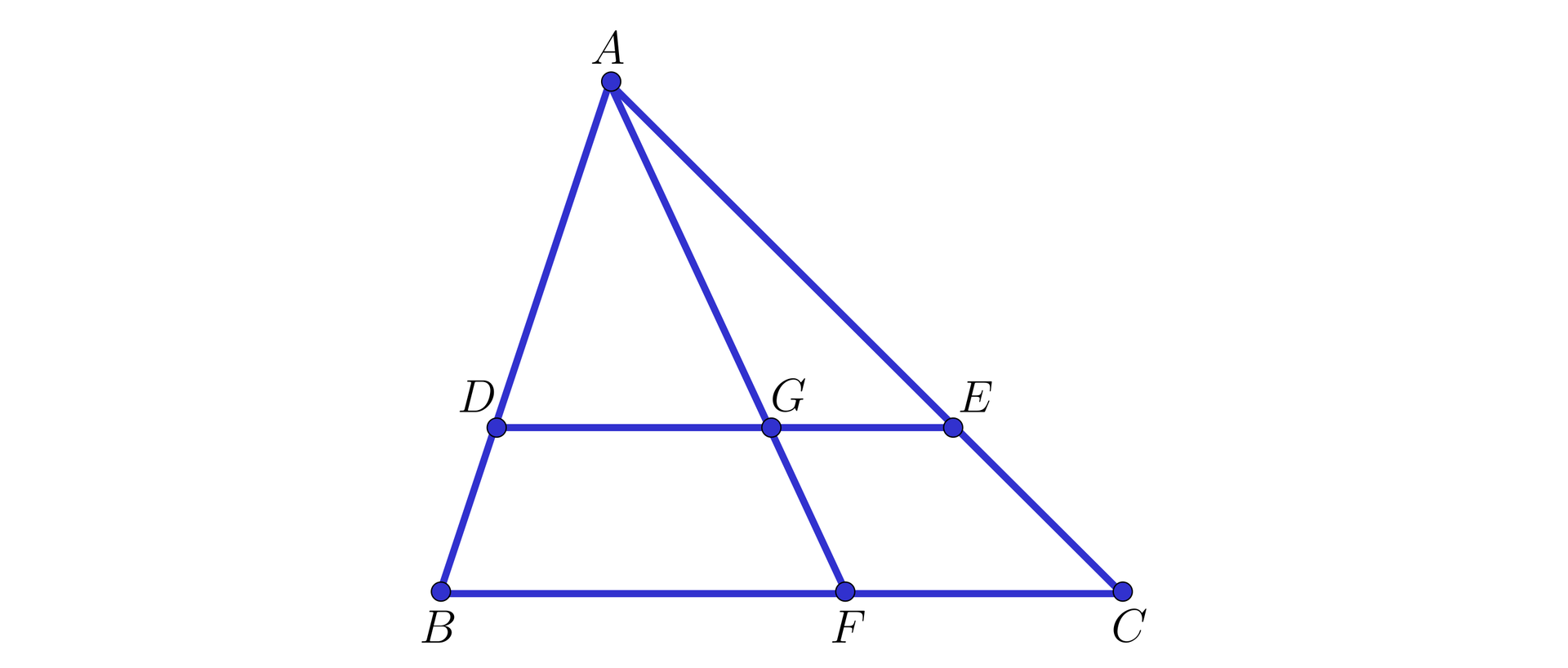
Na ilustracji przedstawiono trójkąt ABC. Na boku AB zaznaczono punkt D. Na boku AC zaznaczono punkt E. Odcinek DE jest równoległy do podstawy BC i znajduje się na około jednej trzeciej wysokości trójkąta. Na podstawie trójkąta zaznaczono punkt F. Poprowadzono prostą AF. Prosta AF przecina prostą DE w punkcie G.

Wyznaczymy długości odcinków $G E$ i $D G$ mając dane długości: $|A E| = 15$ , $|E C| = 9$ , $|F C| = 6$ , $|B F| = 24$ .

Rozwiązanie

$|G E| = \frac{|F C| \cdot |A E|}{|A C|} = \frac{15 \cdot 6}{15 + 9} = 3, 75$

$|D E| = \frac{|B C| \cdot |A E|}{|A C|} = \frac{(24 + 6) \cdot 15}{15 + 9} = 18, 75$

$|D G| = |D E| - |G E| = 15$

Perspektywa w malarstwie

Perspektywa w malarstwie to sposób uzyskania wrażenia głębi na płaskim rysunku. Linie poziome zbiegają się na horyzoncie a linie pionowe zmniejszają się proporcjonalnie do odległości, ale pozostają równoległe. Główną zasadą perspektywy jest to, że pionowe obiekty równej wysokości i równooddalone od siebie przekształca na trapezytrapeztrapezy podobne.

RZ0lBc3F22DrJ

Przedstawiono fotografię pomostu wysuniętego w stronę morza. Zaznaczono linie wzdłuż barier pomostu. Linie przebiegają równolegle i zbiegają się na horyzoncie. — Na obrazie przedstawiona jest fotografia molo w Juracie wraz z zaznaczonymi przykładowymi liniami zbiegającymi się na horyzoncie i odcinkami równoległymi
Źródło: dostępny w internecie: commons.wikimedia.org, licencja: CC BY-SA 3.0.

Przykład 5

Rysunek został wykonany w zgodnie z regułami perspektywy. Latarnie $Q$ , $M$ , $N$ przedstawione na rysunku, mają w rzeczywistości równe wysokości.

Rt0ae6xoz3mpU

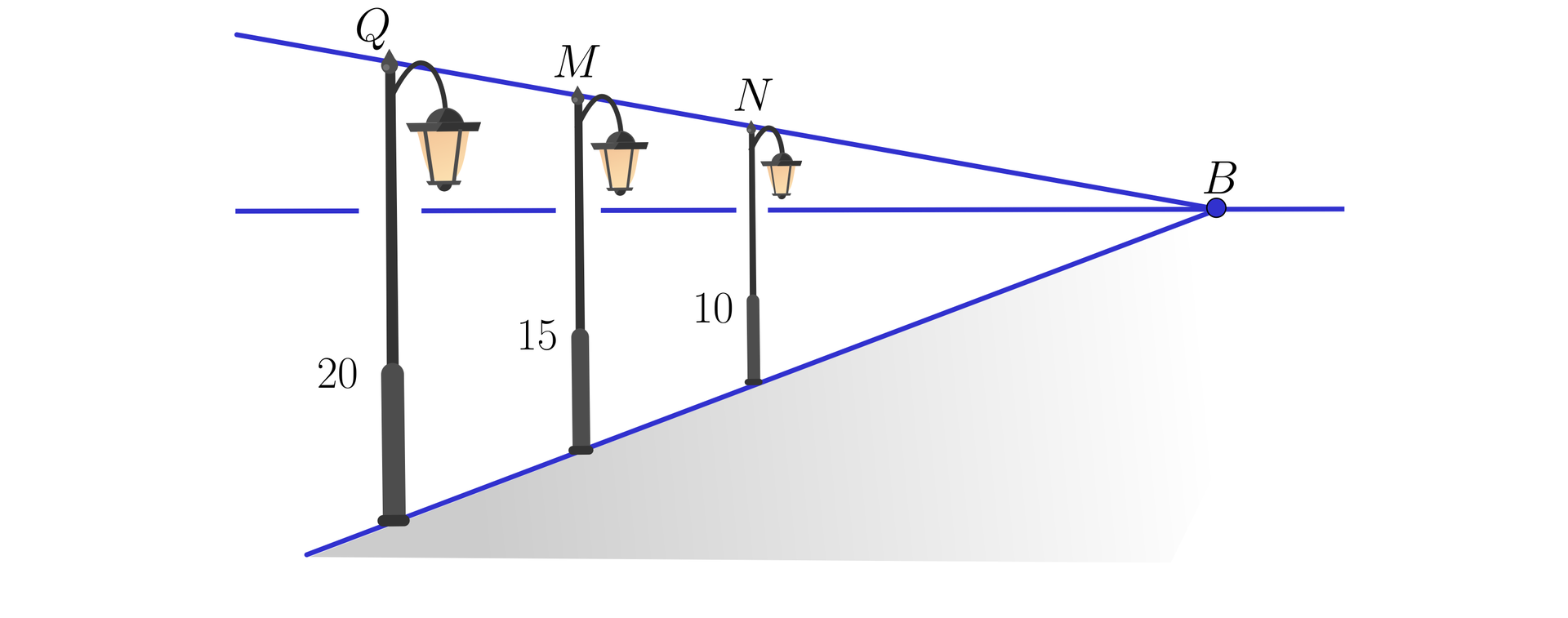
Na ilustracji przedstawiono ramiona wychodzące z punktu B. Przedstawiono 3 latarnie, od lewej kolejno, Q, M, i N, które łączą oba ramiona. Najdalej od punktu B znajduje się latarnia oznaczona literą Q. Ma wysokość dwadzieścia. Następnie znajduje się latarnia oznaczona literą M. Ma wysokość piętnaście. Najbliżej punktu B, znajduje się latarnia oznaczona literą N i ma wysokość dziesięć. Zaznaczono poziomą linie, przecinającą punkt B oraz przedstawione latarnie.

Pokażemy, że w rzeczywistości odległość między latarniami $Q$ i $M$ jest inna niż między $M$ i $N$ .

Niech $Q'$ , $M'$ , $N'$ oznaczają punkty przy podstawie latarni. Gdyby odległości między latarniami $Q$ i $M$ oraz $M$ i $N$ były równe, to trapezy $Q' Q M M'$ oraz $M' M N N'$ byłyby podobne. Wtedy stosunki odpowiednich boków, w szczególności podstaw byłyby równe.

Obliczmy $\frac{|Q' Q|}{|M' M|} = \frac{20}{15} = \frac{4}{3}$ , $\frac{|M' M|}{|N' N|} = \frac{15}{10} = \frac{3}{2}$ . Te stosunki nie są równe, więc w rzeczywistości odległość między latarniami $Q$ i $M$ jest inna niż między $M$ i $N$ .

Załóżmy, że w rzeczywistości przed latarnią $Q$ stoi latarnia $R$ tej samej wysokości, w tej samej linii co latarnie $Q$ i $M$ oraz taka, że odległości między $Q$ , $R$ i $Q$ , $M$ są równe.

Wyznaczymy wysokość obrazu latarni $R$ .

Stosując analogiczne oznaczenia wyznaczymy długość odcinka $R R'$ w oparciu o podobieństwo trapezów $Q' Q M M'$ oraz $R' R M M'$ .

$\frac{|Q' Q|}{|M' M|} = \frac{|R' R|}{|Q' Q|}$ , stąd $|R' R| = \frac{{|Q' Q|}^{2}}{|M' M|} = \frac{20 \cdot 20}{15} = \frac{80}{3} = 26 \frac{2}{3}$

Wyznaczymy długość odcinków $R Q$ , $Q M$ i $M N$ przyjmując, że na rysunku odcinek $B N$ ma długość $30$ .

Z twierdzenia Talesa $\frac{|B N|}{10} = \frac{|B M|}{15} = \frac{|B Q|}{20} = \frac{3 |B R|}{80}$ . Stąd $|B R| = \frac{80 |B N|}{30}$ , $|B Q| = \frac{20 |B N|}{10}$ .

Zatem $|Q R| = |B R| - |B Q| = (\frac{8}{3} - 2) |B N| = \frac{2 \cdot 30}{3} = 20$ .

Wtedy $|B M| = |B N| + |M N| = \frac{15 \cdot |B N|}{10}$ . Stąd $|M N| = \frac{15 \cdot |B N|}{10} - |B N| = \frac{1}{2} |B N| = 15$ .

Podobnie, $|M Q| = \frac{20 |B N|}{10} - |B N| - |M N| =$ $= 2 |B N| - |B N| - \frac{1}{2} |B N| = \frac{1}{2} |B N| = 15$ .

Przykład 6

Na szczeblach drabiny położono poziomo deski w równych odległościach jak na rysunku.

R9dczBmpEPZU5

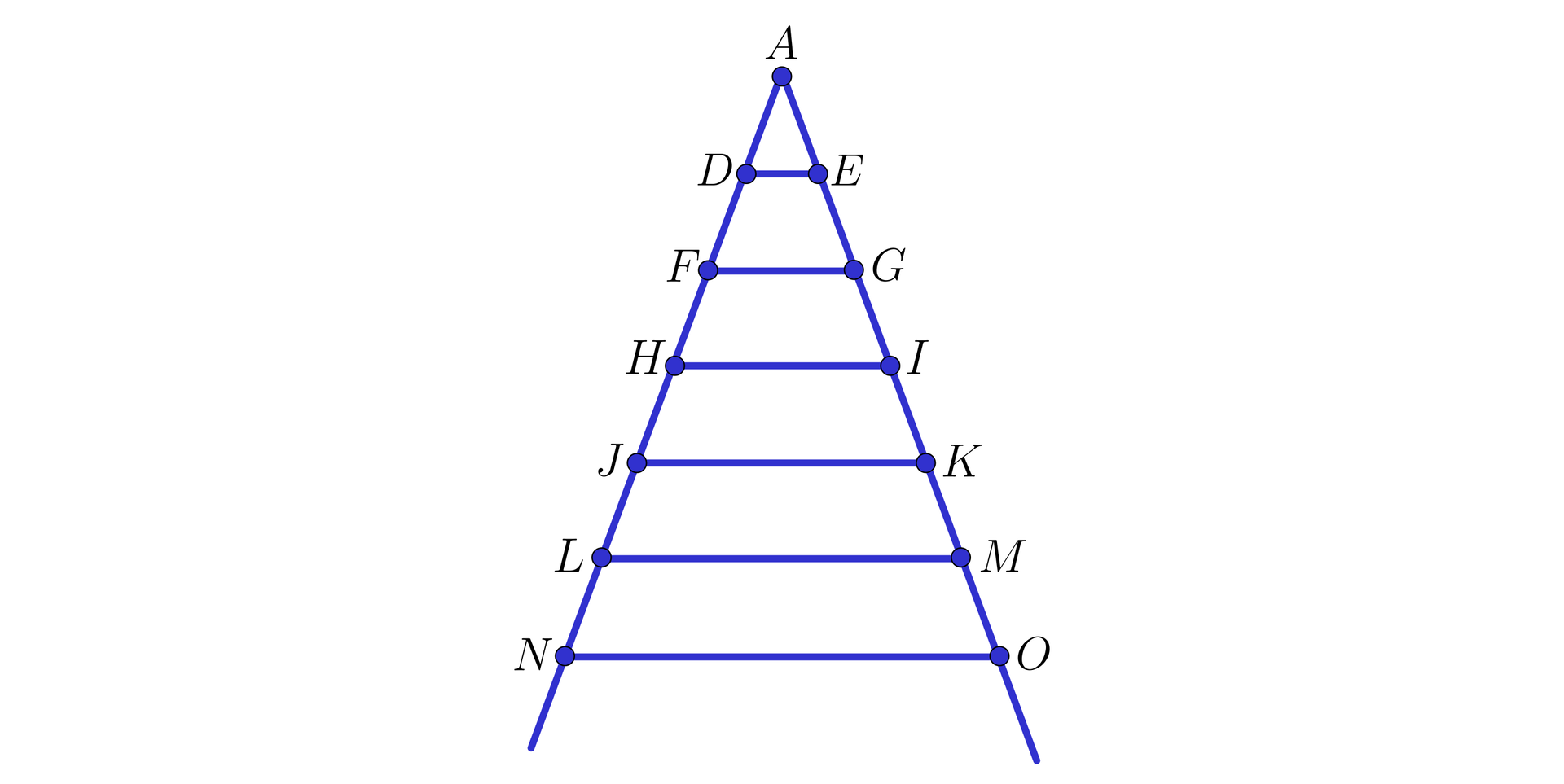
Na ilustracji przedstawiono kąt ostry o wierzchołku A. Poprowadzono odcinki łączące ramiona kąta. Kolejno, zaczynając od odcinka znajdującego się najbliżej wierzchołka A, zaznaczono. Odcinek DE. Odcinek FG. Odcinek HI. Odcinek JK. Odcinek LM. Odcinek NO. Wszystkie odcinki są do siebie równoległe.

Pokażemy, że wszystkie trójkąty o wierzchołku $A$ są podobne do trójkąta $A D E$ .

Rozwiązanie

Rzeczywiście, wszystkie odcinki (deski drabiny) są równolegle do siebie, więc z twierdzenia Talesa każdy z trójkątów o wierzchołku $A$ jest podobny do trójkąta $A D E$ .

Dla zainteresowanych

Spośród trapezów utworzonych na drabinie wybierzemy trapez podobny do trapezu $E D H I$ .

Zakładamy, że drabina tworzy trójkąt równoramienny, więc wszystkie trapezy są równoramienne oraz odcinki $A N$ i $A O$ są równe i każdy z nich jest podzielony na $6$ równych odcinków długości $x$ . Niech $y$ oznacza długość odcinka $D E$ . Wtedy z twierdzenia Talesa $|F G| = 2 y$ , $|H I| = 3 y$ itd., więc każdy odcinek poziomy ma długość $m y$ , gdzie $m \in \{1, 2, 3, 4, 5, 6\}$ .

R9dczBmpEPZU5

Z własności prostych równoległych, wszystkie trapezy na rysunku mają odpowiednie kąty równe. Wystarczy więc sprawdzić warunek, że stosunki odpowiednich boków są równe.

Jeśli trapez $X Y Z T$ jest podobny do trapezu $E D H I$ , to istnieje $k$ takie, że

$|X Y| = k |D E| = k y$ , $|Z T| = k |H I| = 3 k y$ , $|X Z| = k |D H| = 2 k x$

Z drugiej strony, krótsza podstawa $|X Y| = k y = m y$ , gdzie $m \in \{1, 2, 3, 4, 5\}$ , więc $k \in \{1, 2, 3, 4, 5\}$ .

Jeśli $k = 1$ , to dostajemy trapez $E D H I$ . Jeśli $k = 2$ , to $|Z T| = 6 y$ i wtedy dostajemy trapez $F G N O$ . Trzeba jeszcze sprawdzić ramiona tego trapezu: $|F N| = 4 x = 2 \cdot 2 x = 2 k x$ .

Pokazaliśmy, że trapez $F G N O$ jest podobny do trapezu $E D H I$ .

Innych trapezów podobnych nie ma, bo jeśli $k > 2$ , to $3 k > 6$ , a odcinka poziomego takiej długości nie ma na rysunku.

Słownik

jednokładność

o środku $O$ i skali $k \neq 0$ jest to przekształcenie płaszczyzny, które dowolnemu punktowi $P$ przyporządkowuje taki punkt $P'$ , że $|O P| = |k| \cdot |O P'|$

cechy podobieństwa trójkątów

warunki konieczne i wystarczające na to, aby dwa trójkąty były podobne

cecha podobieństwa bok – bok – bok

jeżeli boki jednego trójkąta są proporcjonalne do odpowiednich boków drugiego trójkąta, to trójkąty są podobne

cecha podobieństwa kąt – kąt – kąt

jeżeli miary dwóch kątów jednego trójkąta są równe miarom dwóch kątów drugiego trójkąta, to trójkąty są podobne

cecha podobieństwa bok – kąt – bok

jeżeli dwa boki jednego trójkąta są proporcjonalne do odpowiednich dwóch boków drugiego trójkąta, a kąty między nimi zawarte są przystające, to trójkąty są podobne

cechy przystawania trójkątów

to warunki konieczne i wystarczające na to, aby dwa trójkąty były przystające

cecha przystawania bok‑bok‑bok

przystawanie odpowiednich boków

cecha przystawania bok‑kąt‑bok

przystawanie dwóch boków i kąta między nimi

cecha przystawania kąt‑bok‑kąt

przystawanie dwóch kątów i boku będącego ramionami kątów

cecha przystawania bok‑bok‑kąt

przystawanie dwóch boków i kąta naprzeciw dłuższego z nich

cecha przystawania bok‑kąt‑kąt

przystawanie dwóch kątów i boku leżącego naprzeciw wskazanego spośród nich

trapez

czworokąt, który ma co najmniej jedną parę boków równoległych

równoległobok

czworokąt, który ma dwie pary boków równoległych

punkty współliniowe

co najmniej $3$ punkty, które leżą na jednej prostej

Wprowadzenie

Symulacja interaktywna

Własności relacji podobieństwa

Skala podobieństwa i jej własności

Cechy podobieństwa trójkątów

Twierdzenie Talesa wynika z podobieństwa trójkątów

Twierdzenie odwrotne do twierdzenia Talesa wynika z podobieństwa trójkątów

Perspektywa w malarstwie

Słownik