Przeczytaj

Rozważmy trójkąt o wierzchołkach w punktach $A = (x_{A}; y_{A})$ , $B = (x_{B}; y_{B})$ , $C = (x_{C}; y_{C})$ . Zauważmy, że jeśli odcinek $B C$ jest równoległy do osi $X$ , to równanie prostej przechodzącej przez wierzchołek $A$ zawierającej wysokość tego trójkąta to $x = x_{A}$ .

RzEcgglYEGsXS

Ilustracja przedstawia układ współrzędnych z poziomą osią X od -5 do pięć oraz z pionową osią Y od -1 do sześć. W pierwszej i w drugiej ćwiartce zaznaczono trzy punkty: A=xA;yA, B=xB;yB, C=xC;yC. Połączono punkty, tworząc trójkąt A B C. Odcinek B C jest równoległy do osi X. Zaznaczono pionową prostą przebiegającą przez punkt A, która pokrywa się z wysokością trójkąta upuszczoną na poziomą podstawę B C.

Jeśli odcinek $B C$ nie jest równoległy do osi $X$ , to współczynnik kierunkowy prostej $B C$ jest równy ilorazowi różnicy drugich współrzędnych punktów $C$ i $B$ przez różnicę pierwszych współrzędnych tych punktów (w tej samej kolejności), czyli $\frac{y_{C} - y_{B}}{x_{C} - x_{B}}$ .

RodbIhdXzZRvY

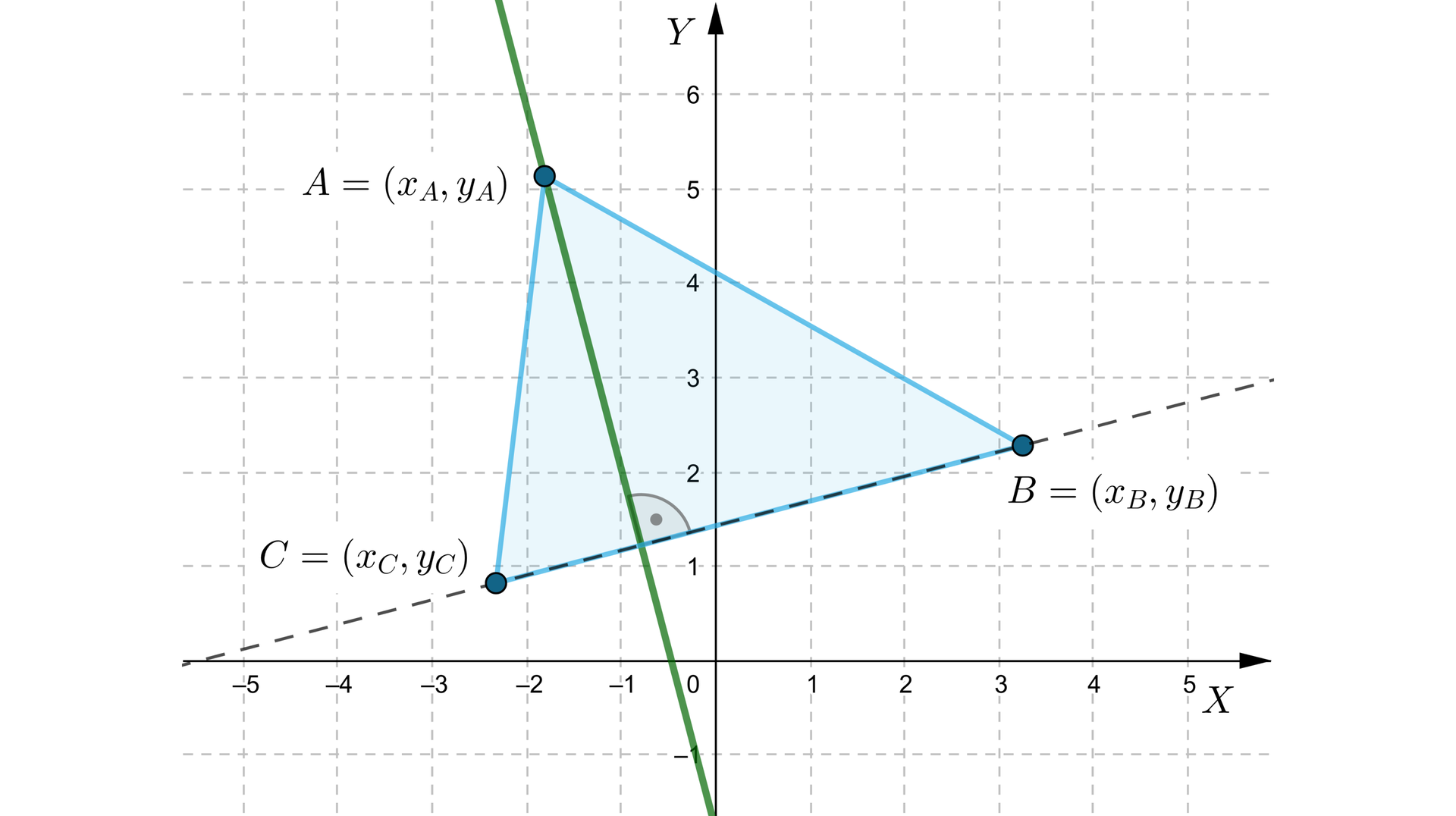
Ilustracja przedstawia układ współrzędnych z poziomą osią X od -5 do pięć oraz z pionową osią Y od -1 do sześć. W pierwszej i drugiej ćwiartce zaznaczono trzy punkty: A=xA;yA, B=xB;yB, C=xC;yC. Połączono ze sobą punkty, tworząc trójkąt A B C. Przerywaną linią zaznaczono ukośną prostą, która przechodzi przez punkty B oraz C. Zaznaczono ukośną prostą, która pokrywa wysokość trójkąta upuszczoną na podstawę B C i przechodzącą przez punkt A.

Ponieważ prosta zawierająca wysokość poprowadzoną z punktu $A$ jest prostopadła do prostej $B C$ , więc jej współczynnik kierunkowy jest równy $- \frac{x_{C} - x_{B}}{y_{C} - y_{B}}$ . Po zastosowaniu wzoru na równanie prostej o danym współczynniku kierunkowym przechodzącej przez dany punkt, otrzymujemy równanie prostej
$y - y_{A} = - \frac{x_{C} - x_{B}}{y_{C} - y_{B}} (x - x_{A})$ ,
co po przekształceniu daje równanie
$(y_{C} - y_{B}) (y - y_{A}) = - (x_{C} - x_{B}) (x - x_{A})$ .

Sprawdźmy jeszcze otrzymany ostatecznie wzór obejmuje również przypadek, gdy odcinek $B C$ jest równoległy do osi $X$ . Wówczas $y_{B} = y_{C}$ i $x_{B} \neq x_{C}$ (w przeciwnym razie nie otrzymalibyśmy trójkąta), więc roważany wzór przyjmuje postać
$(y_{C} - y_{C}) (y - y_{A}) = - (x_{C} - x_{B}) (x - x_{A})$
$0 = - (x_{C} - x_{B}) (x - x_{A})$
$x = x_{A}$ .

Zatem wzór
$(y_{C} - y_{B}) (y - y_{A}) = - (x_{C} - x_{B}) (x - x_{A})$
opisuje prostą zawierającą wysokość trójkątawysokość trójkątawysokość trójkąta o wierzchołkach
$A = (x_{A}; y_{A})$ , $B = (x_{B}; y_{B})$ , $C = (x_{C}; y_{C})$
przechodzącą przez punkt $A$ niezależnie od położenia punktów $A$ , $B$ , $C$ w prostokątnym układzie współrzędnych.

Przykład 1

Wyznaczymy równanie prostej zawierającej wysokość trójkątawysokość trójkątawysokość trójkąta o wierzchołkach $A = (- 1; - 3)$ , $B = (8; 3)$ , $C = (2; 6)$ przechodzącej przez punkt $A$ .

Możemy wykorzystać otrzymany wzór.

$(y_{C} - y_{B}) (y - y_{A}) = - (x_{C} - x_{B}) (x - x_{A})$
$(6 - 3) (y + 3) = - (2 - 8) (x + 1)$
$3 (y + 3) = 6 (x + 1)$
$3 y + 9 = 6 x + 6$
$y + 3 = 2 x + 2$
$y = 2 x - 1$

Możemy też powtórzyć całą drogę, która doprowadziła nas do tego wzoru:

współczynnik kierunkowy prostej $B C$ jest równy
$\frac{6 - 3}{2 - 8} = \frac{3}{- 6} = - \frac{1}{2}$ ,
współczynnik kierunkowy prostej zawierającej wysokość poprowadzoną do boku $B C$ jest równy $2$ ,
korzystając ze wzoru na równanie prostej o danym współczynniku kierunkowym przechodzącej przez dany punkt, otrzymujemy równanie
$y + 3 = 2 (x + 1)$ ,
co po przekształceniu daje równanie
$y = 2 x - 1$ .

R16183b1LbJfG

Ilustracja przedstawia dwuwymiarowy układ współrzędnych z osią poziomą X od -4 do dziewięć oraz osią pionową Y od -4 do osiem. Zaznaczono punkty: A=-1;-3, B=8;3 oraz C=2;6. Połączono te trzy punkty, tworząc trójkąt A B C. Przez punkty B C poprowadzono przerywaną linią prostą. Zaznaczono prostą, która pokrywa wysokość trójkąta upuszczoną na bok B C, przechodzącą przez punkt A.

Przykład 2

Wyznaczymy współrzędne punktu przecięcia wysokości (tzw. ortocentrum) trójkąta o wierzchołkach $A = (- 1; - 3)$ , $B = (8; 3)$ , $C = (2; 6)$ .

W poprzednim przykładzie wyznaczyliśmy równanie prostej zawierającej wysokość poprowadzoną z wierzchołka $A$ : $y = 2 x - 1$ .

Wyznaczmy równanie prostej zawierającej wysokość poprowadzoną z wierzchołka $B$ :

$(6 - (- 3)) (y - 3) = - (2 - (- 1)) (x - 8)$
$9 (y - 3) = - 3 (x - 8)$
$y = - \frac{1}{3} x + \frac{17}{3}$

Na mocy twierdzenia, które orzeka, że wszystkie trzy proste zawierające wysokości trójkąta przecinają się w jednym punkcie, wystarczy, że wyznaczymy współrzędne punktu wspólnego dwóch z nich. W tym celu wystarczy rozwiązać układ złożony z równań dwóch prostych zawierających wysokości:

$\{\begin{cases} y = - \frac{1}{3} x + \frac{17}{3} \\ y = 2 x - 1 \end{cases}$

Z układu wynika równanie

$- \frac{1}{3} x + \frac{17}{3} = 2 x - 1$ ,

które można przekształcić następująco

$- x + 17 = 6 x - 3$
$- 7 x = - 20$
$x = \frac{20}{7}$

Dla $x = \frac{20}{7}$ , mamy
$y = 2 \cdot \frac{20}{7} - 1 = \frac{33}{7}$ .
Zatem ortocentrum trójkątaortocentrum trójkątaortocentrum trójkąta $A B C$ ma współrzędne $(\frac{20}{7}; \frac{33}{7})$ .

Słownik

wysokość trójkąta

odcinek o jednym końcu w wierzchołku tego trójkąta o drugim końcu na prostej zawierającej przeciwległy bok prostopadły do tego boku

ortocentrum trójkąta

punkt przecięcia prostych zawierających wysokości trójkąta

Wprowadzenie

Aplet

Słownik