Przeczytaj
Przypomnijmy, że z definicji figur podobnych wynika, że jeśli trójkąt jest obrazem trójkąta w podobieństwie o skali , przy czym punkty , i są obrazami punktów odpowiednio , i w tym podobieństwie, to

Równości te możemy zapisać w postaci
Możemy zatem powiedzieć, że skala podobieństwa trójkątów to stosunek długości boku trójkąta będącego obrazem do boku trójkąta wyjściowego. Pokażemy, że skalę podobieństwa trójkątów możemy wyznaczyć, obliczając stosunek długości innych odpowiadających sobie wielkości w tych trójkątach, na przykład obwodów tych trójkątów.
Ponieważ
więc
Podobnie możemy wykazać, że skala podobieństwa trójkąta do trójkąta jest równa stosunkowi opowiadających sobie wysokości tych trójkątów lub stosunkowi długości odpowiadających sobie środkowych.
Zauważmy też, że jeżeli skala podobieństwa trójkąta do trójkąta jest równa , to skala podobieństwa trójkąta do trójkąta jest równa .
Pokażemy teraz ważną własność pól trójkątów podobnych.
Stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa tych trójkątów.
Niech będzie skalą podobieństwa trójkąta do trójkąta .
Wówczas i .
Oznaczmy .
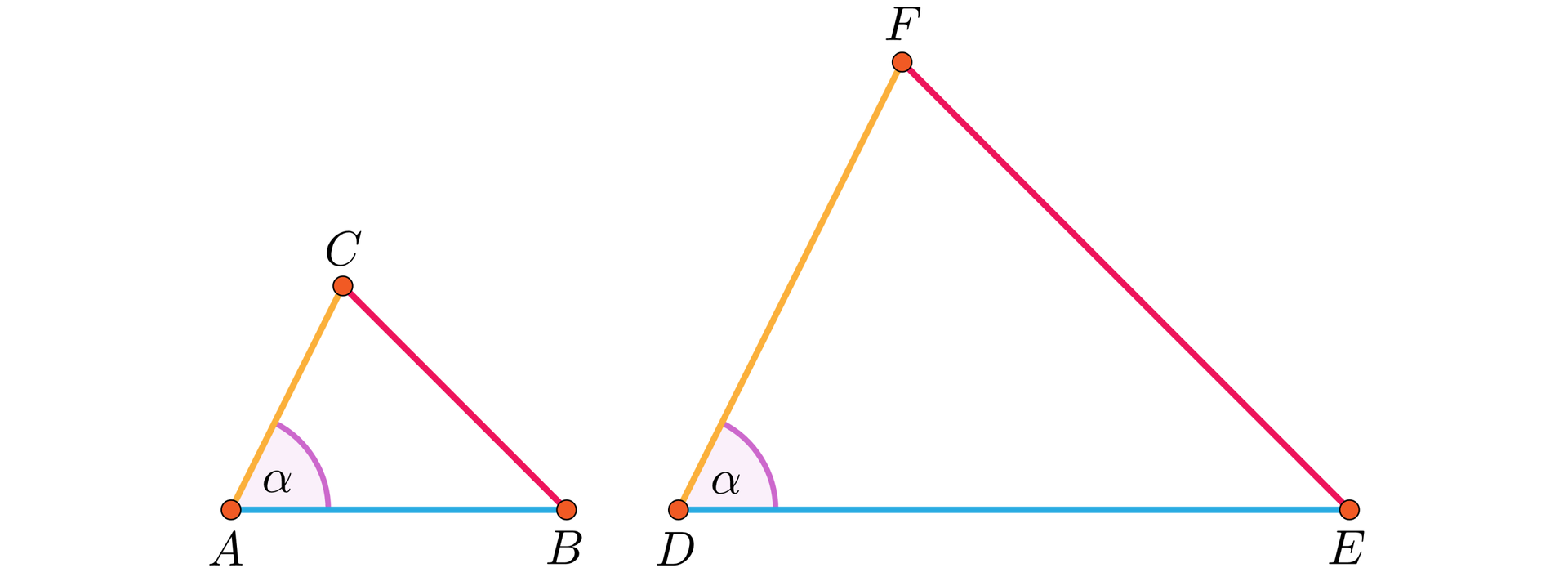
Stosunek pól trójkątów i jest równy
To kończy dowód.
Ta sama własność jest też prawdziwa w przypadku dowolnych figur podobnych. Jej dowód w przypadku wielokątów wynika z faktu, że każdy wielokąt można podzielić na parami rozłączne trójkąty.
Nie trudno też zauważyć, że stosunek objętości brył podobnych jest równy sześcianowi ich skali podobieństwa.
Szczególnym przypadkiem figur podobnych są figury przystające. Skala ich podobieństwa jest równa .
Relacja podobieństwa figur jest:
Zwrotna, tzn. każda figura jest podobna do samej siebie. Możemy to zapisać .
Symetryczna, tzn. jeżeli figura jest podobna do figury , to figura jest podobna do figury . Możemy to zapisać: jeżeli , to .
Przechodnia, tzn. jeżeli figura jest podobna do figury i figura jest podobna do figury , to figura jest podobna do figury . To możemy zapisać: jeżeli i , to .
Pokażemy kilka przykładów, w których wykażemy, że trójkąty są podobne lub wykorzystamy podobieństwo trójkątów.
Trójkąt jest prostokątny. Punkt jest spodkiem wysokościspodkiem wysokości opuszczonej z wierzchołka kąta prostego tego trójkąta.
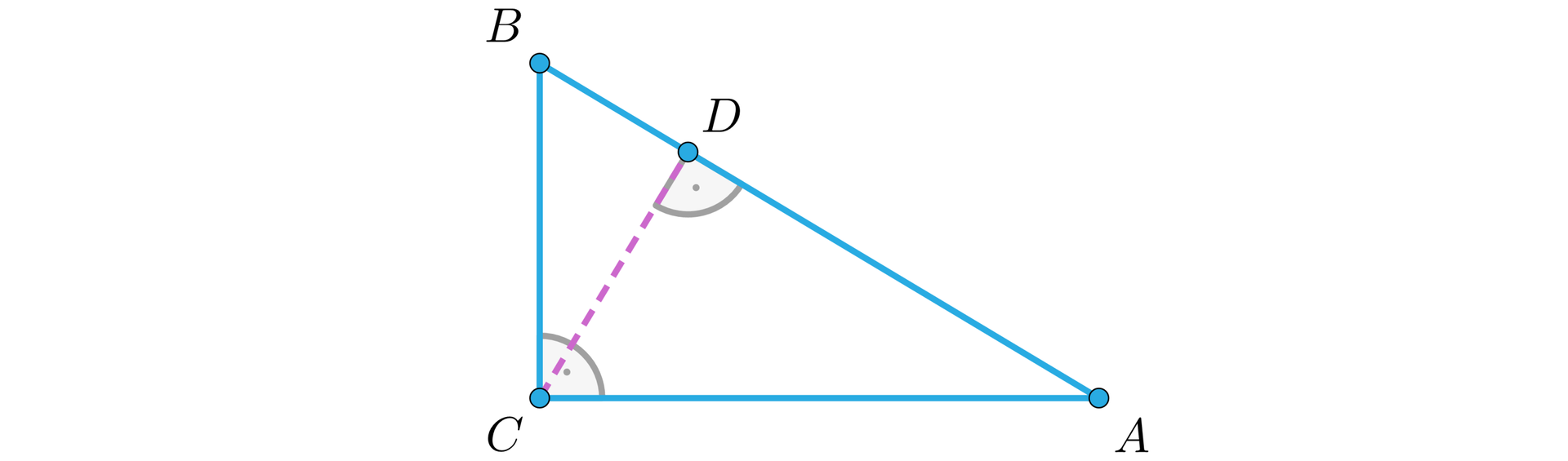
Wykaż, że trójkąty , i są podobne.
Rozwiązanie
Oznaczmy .
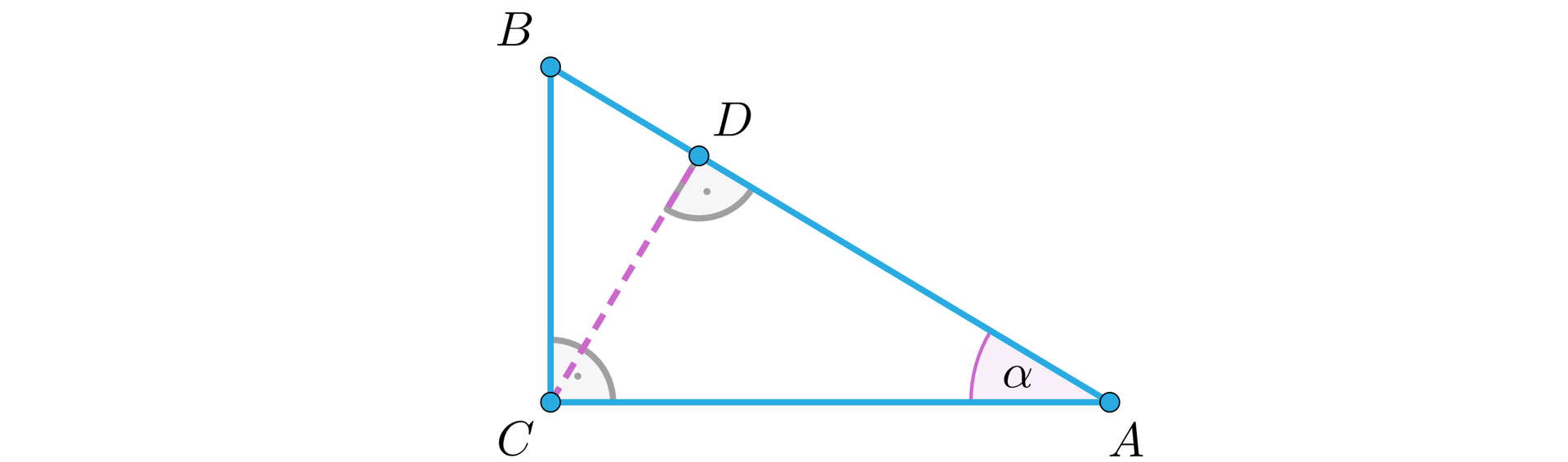
Trójkąty i są prostokątne, mają wspólny kąt ostry przy wierzchołku , więc z twierdzenia o sumie kątów trójkąta otrzymujemy oraz .
Zatem .
Zatem z cechy kkk wynika, że trójkąty i są podobne.
Trójkąt jest prostokątny oraz , więc z twierdzenia o sumie kątów trójkąta otrzymujemy .
Wobec tego kąty trójkąta są takie same jak kąty trójkątów i , co oznacza, że trójkąt jest podobny do każdego z trójkątów i .
To należało wykazać.
Trójkąt jest podobny do trójkąta w skali , trójkąt jest podobny do trójkąta w skali . Oblicz skalę podobieństwa trójkąta do trójkąta .
Rozwiązanie
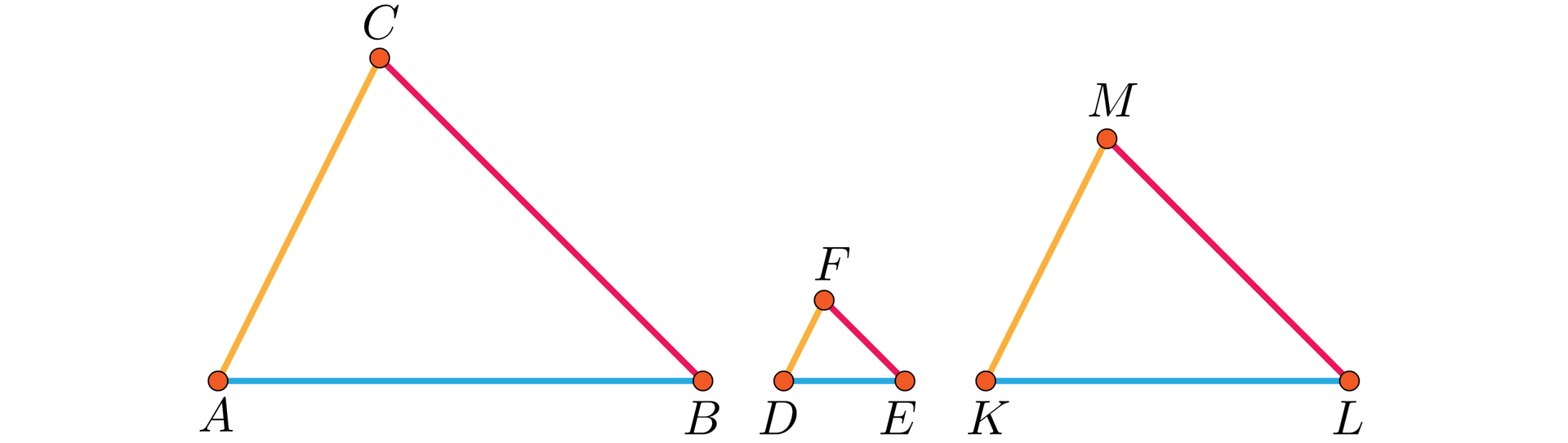
Ponieważ skala podobieństwa trójkąta do trójkąta jest równa , więc .
Skala podobieństwa trójkąta do trójkąta jest równa , więc .
Skala podobieństwa trójkąta do trójkąta jest równa .
Trójkąt jest równoboczny. Punkty , i leżą na bokach odpowiednio , i tego trójkąta oraz . Odcinki , i wyznaczają trójkąt , jak na rysunku.
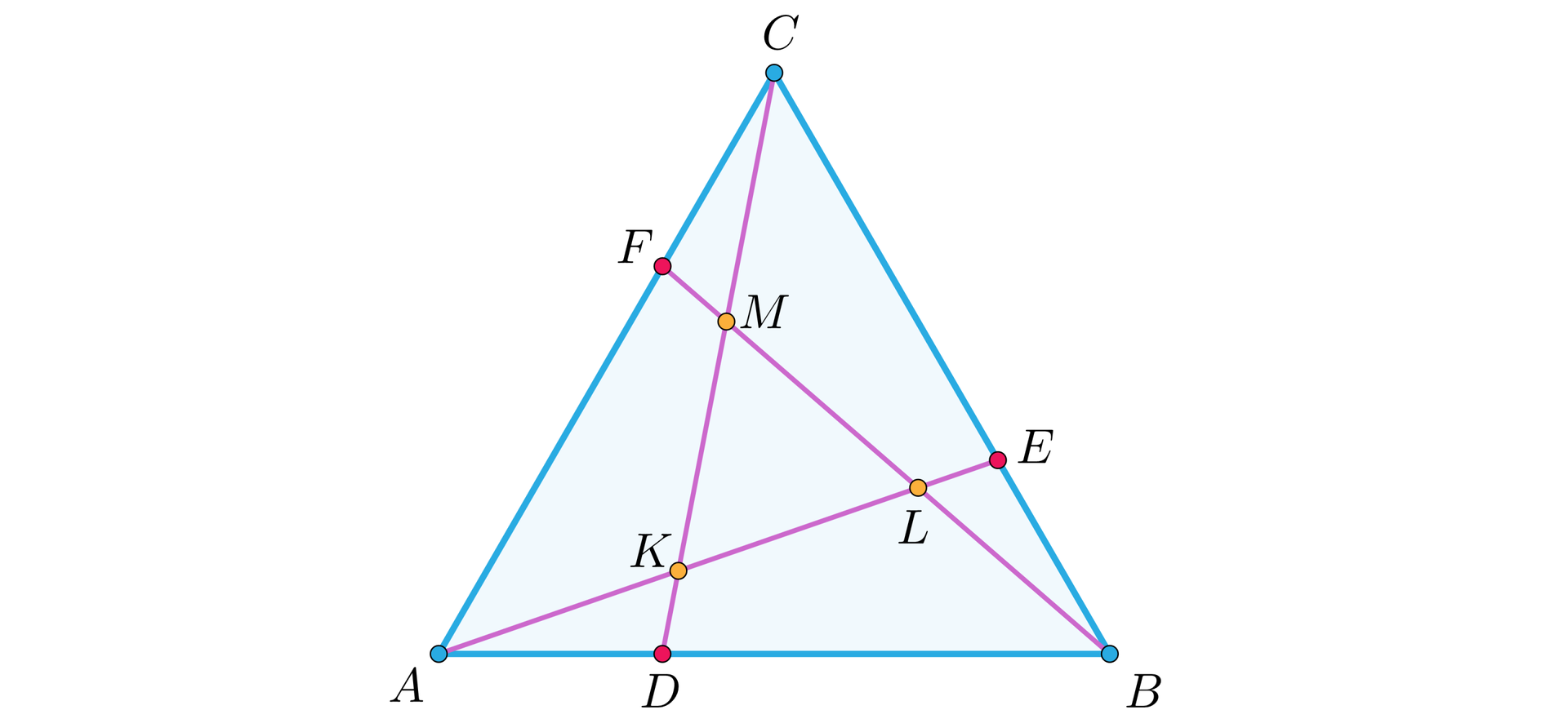
Wykaż, że trójkąt jest podobny do trójkąta i oblicz skalę tego podobieństwa.
Rozwiązanie
Aby wykazać, że trójkąt jest podobny do trójkąta wystarczy wykazać, że trójkąt jest równoboczny.
Oznaczmy przez długość boku trójkąta . Wtedy
oraz .
Stąd i z równości wynika, na mocy cechy bkb, że trójkąty , i są przystające. Stąd otrzymujemy
oraz .
To z kolei, wraz z równością , oznacza, że trójkąty , i są przystające (cecha kbk).
Wobec tego .
Ponieważ , i , gdyż są to pary kątów wierzchołkowych, więc .
Zatem trójkąt jest równoboczny.
Obliczmy teraz skalę podobieństwa tego trójkąta do trójkąta . Skala ta jest równa stosunkowi długości boków tych trójkątów. Ponieważ trójkąt jest równoboczny, więc .
Trójkąt jest podobny do trójkąta , ponieważ: (kąt wspólny), oraz (cecha kkk).
Zatem , skąd , ale , więc .
Trójkąty i są podobne, gdyż mają wspólny kąt przy wierzchołku oraz .
Zatem , skąd , ale , więc .
Zatem . Stąd , czyli , więc , ale , wobec tego .
Zatem .
Z twierdzenia cosinusów dla trójkąta otrzymujemy
Stąd .
Wobec tego .
Zatem skala podobieństwa trójkąta do trójkąta jest równa .
Trójkąt jest prostokątny. Punkt jest spodkiem wysokości opuszczonej z wierzchołka kąta prostego tego trójkąta.
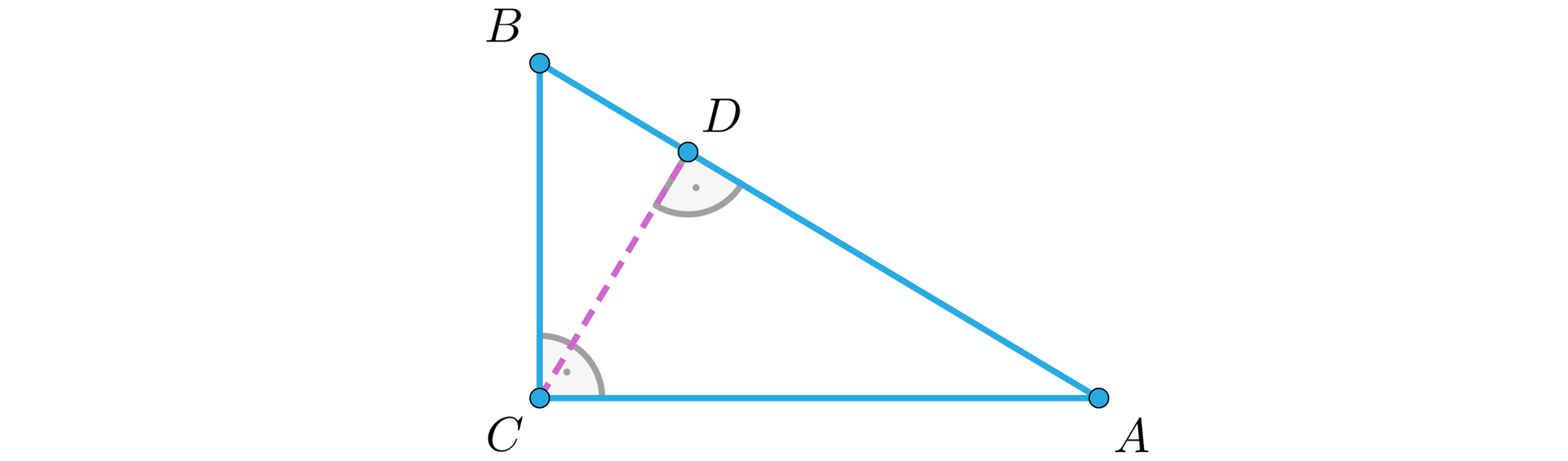
Udowodnij, że obwody trójkątów , i spełniają równość
.
Dowód
Trójkąty , i są podobne, co wykazaliśmy w przykładzie 1. Pole trójkąta jest równe sumie pól trójkątów , , czyli
.
Stąd, dzieląc obie strony tej równości przez , otrzymujemy
.
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa tych figur, a skala podobieństwa figur podobnych jest równa stosunkowi obwodów tych figur, więc powyższą równość możemy zapisać w postaci
, czyli .
Stąd, mnożąc obie strony otrzymanej równości przez , otrzymujemy
.
To kończy dowód.
Słownik
punkt wspólny wysokości i prostej, na którą ta wysokość została opuszczona