Świecę w kształcie kuli o promieniu $6 \mathrm{cm}$ przetopiono na świecę w kształcie stożka o wysokości $10 \mathrm{cm}$. Obliczymy, jaką długość ma promień podstawy tego stożka.

R7MIM8crqoEea

Ilustracja przedstawia fioletową świecę w kształcie kuli.

R1bbiUdvVAduD

Ilustracja przedstawia pomarańczową świecę w kształcie stożka.

Rozwiązanie:

Obliczamy objętość kuli: $V=\frac{4}{3}\pi \cdot 6^3=288\pi$.

Obliczamy długość podstawy stożka podstawiając dane do wzoru na objętość: $\frac{1}{3}\pi \cdot r^2\cdot 10=288\pi$, a stąd $r^2=86,4$, co daje nam $r\approx 9,3 \mathrm{cm}$.

Półkolista równoważnia jest wykonana z tworzywa o gęstości $74 \frac{\mathrm{kg}}{{\mathrm{m}}^3}$ i ma średnicę długości $6 \mathrm{dm}$. Wyznaczymy masę tej równoważni. Wynik przybliżymy do $0,1 \mathrm{kg}$. Przyjmiemy: $\pi =3,14$.

R1RVwTKWfawrc

Ilustracja przedstawia plac zabaw w parku gdzie do stworzenia paru obiektów użyto kształtu kuli.

Rozwiązanie:

Obliczamy objętość półkuli: $V=\frac{2}{3}\pi \cdot 3^3=18\pi \approx 56,52 {\mathrm{dm}}^3\approx 0,057 {\mathrm{m}}^3$.

A zatem masa równoważni wynosi $m=0,057\cdot 74\approx 4,2 \mathrm{kg}$.

Kasia kupiła styropianową kulę o średnicy $30 \mathrm{cm}$, z której wykona bombkę choinkową metodą decoupage. Obliczymy, ile serwetek o wymiarach $33 \mathrm{cm}\times 33 \mathrm{cm}$ potrzebuje, jeżeli do powierzchni kuli należy dorzucić jeszcze $10\%$ powierzchni na zakładki i ścinki.

Rozwiązanie:

Obliczamy pole powierzchni kuli: $P_c=4\cdot \pi \cdot 225\approx 2826 {\mathrm{cm}}^2$. Razem z zakładkami ścinkami mamy więc $3108,6 {\mathrm{cm}}^2$.

Pole powierzchni jednej serwetki wynosi $33\cdot 33=1089 {\mathrm{cm}}^2$.

Stąd otrzymujemy $3108,6:1089\approx 2,85$. A zatem Kasia potrzebuje $3$ takich serwetek.

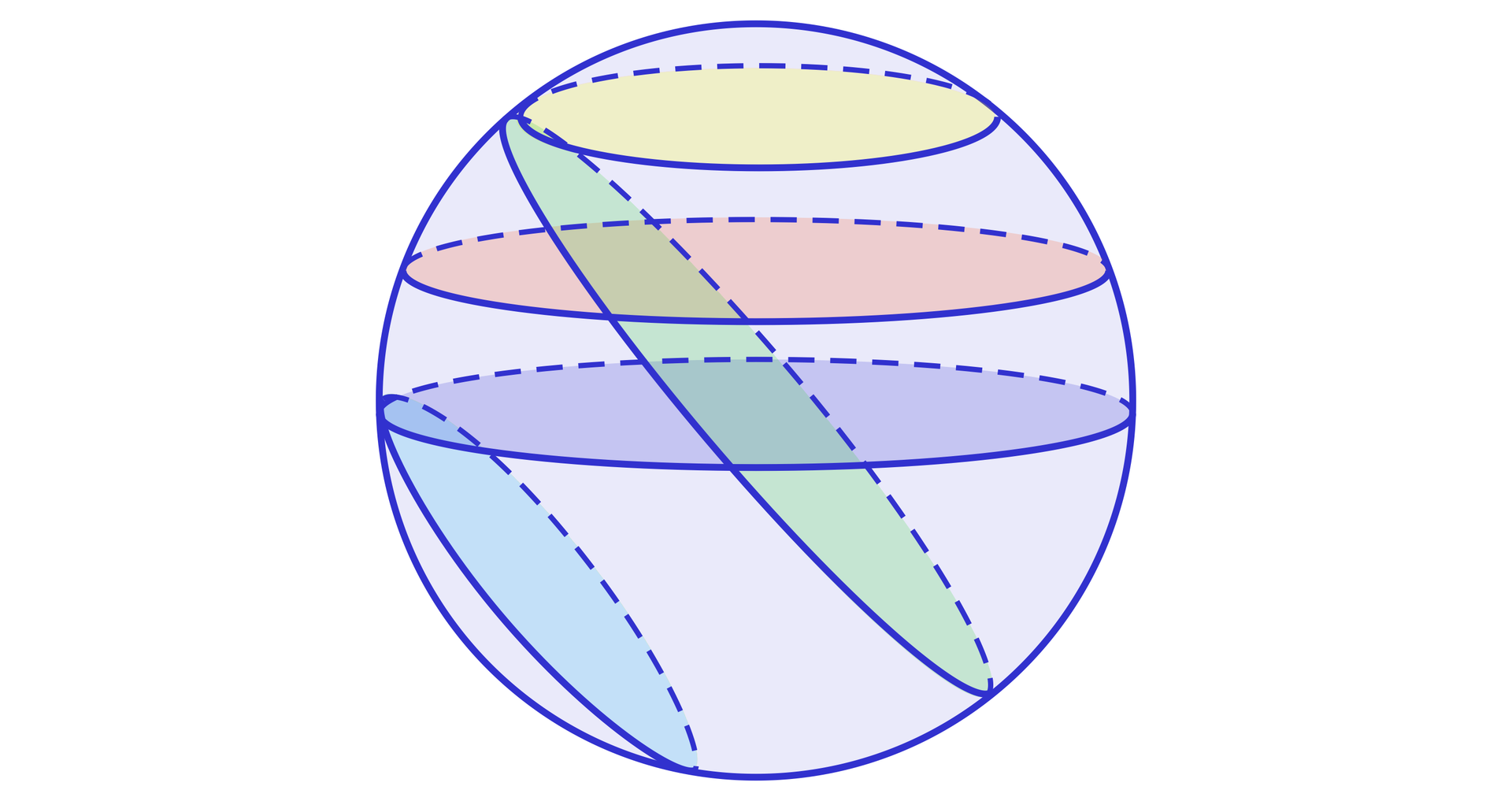
Akwarium w kształcie czaszy wyciętej ze sferysferasfery o średnicy $40 \mathrm{cm}$ jest napełnione wodą tak, że promień powierzchni wody wynosi $2 \mathrm{dm}$. Obliczymy, ile wody jest w akwarium. Wynik przybliżymy do $0,1 \mathrm{l}$. Przyjmiemy $\pi =3,14$.

RbUgd2QaF1y0e

Zdjęcie przedstawia akwarium z roślinkami i rybką w środku.

Rozwiązanie:

Powierzchnia wody jest przekrojem osiowym kuliprzekrój osiowyprzekrojem osiowym kuli. A zatem musimy obliczyć objętość półkuli o promieniu $2 \mathrm{dm}$. $V_{\text{półkuli}}=\frac{2}{3}\pi \cdot 8\approx 16,7 \mathrm{l}$.

Przecięto $100$ drewnianych polakierowanych klocków w kształcie kuli o średnicy $20 \mathrm{cm}$ w odległości $6 \mathrm{cm}$ od środka a następnie dokończono lakierowanie powstałych klocków. Czy puszka o pojemności $0,5 \mathrm{l}$ wystarczy na polakierowanie tych klocków, jeżeli wydajność lakieru wynosi $10 \frac{{\mathrm{m}}^2}{\mathrm{l}}$.

Rozwiązanie:

R1QcnOa1MXBIF

Ilustracja przedstawia kulę o promieniu 10, w której wycięto poziomy przekrój w kształcie koła o promieniu r. Rysując promień kuli prostopadły do przekroju, otrzymujemy, że środek przekroju oddalony jest od środka kuli o sześć. Powstaje więc trójkąt prostokątny o przyprostokątnych r oraz 6 i o przeciwprostokątnej długości dziesięć.

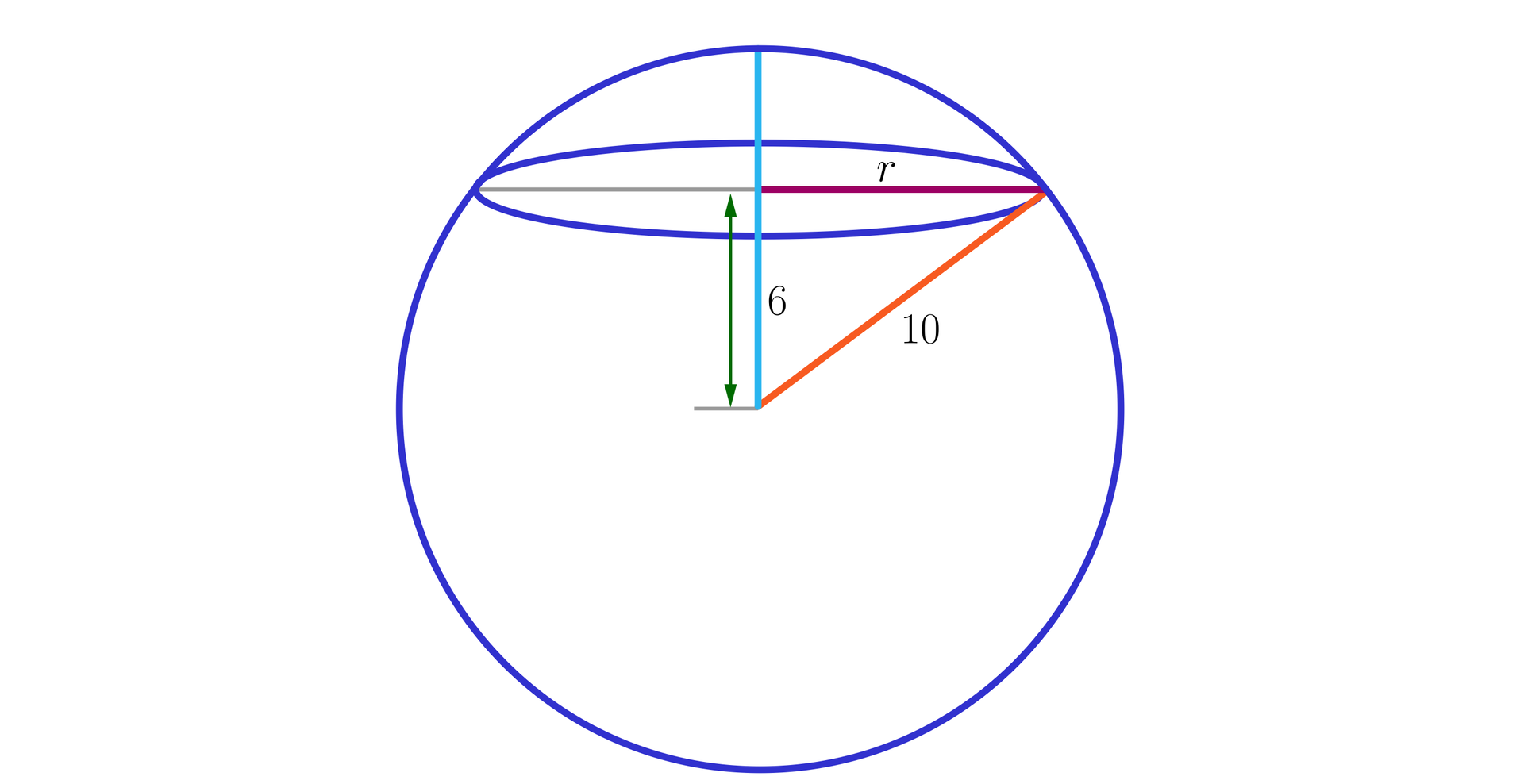
Obliczymy promień przekroju z twierdzenia Pitagorasa: $6^2+r^2={10}^2$, a stąd $r=8 \mathrm{cm}$.

Musimy więc polakierować $200$ kół o promieniu długości $8 \mathrm{cm}$. A stąd $P=200\cdot \pi \cdot 8^2\approx 40192 {\mathrm{cm}}^2\approx 4,02 {\mathrm{m}}^2$.

Farbą z puszki o objętości $0,5 \mathrm{l}$ możemy pomalować $5 {\mathrm{m}}^2$ farby. A zatem puszka ta wystarczy na dokończenie malowania powstałych klocków.

Dla zainteresowanych - treść wykracza poza podstawę programową.

część wspólna tej bryły obrotowej z płaszczyzną zawierającą jej oś obrotu

powierzchnia kuli

przekrój kuli przechodzący przez środek kuli