Funkcję wymiernąfunkcja wymiernaFunkcję wymierną postaci $f\left(x\right)=\frac{ax+b}{cx+d}$, gdzie $c\ne 0$ i $ad-cb\ne 0$ nazywamy funkcją homograficzną.

Dziedziną funkcji homograficznej jest zbiór $\mathrm{ℝ}\setminus \left\{-\frac{d}{c}\right\}$.

Powyższy wzór to postać ogólna funkcji homograficznej.

Postać kanoniczna funkcji homograficznej

$f\left(x\right)=\frac{r}{x-p}+q$, $r\ne 0$, $D_f=\mathrm{ℝ}\setminus \left\{p\right\}$.

Wykresem każdej funkcji homograficznej jest hiperbola.

Wykres funkcji $f\left(x\right)=\frac{r}{x-p}+q$ powstaje w wyniku przesunięcia wykresu funkcji $g\left(x\right)=\frac{r}{x}$ o wektor $\left[p,q\right]$.

AsymptotamiasymptotaAsymptotami wykresu funkcji $f\left(x\right)=\frac{r}{x-p}+q$ są proste o równaniach:

$x=p$ – asymptota pionowa

$y=q$ – asymptota pozioma

Przekształcimy wzór funkcji $f\left(x\right)=\frac{5}{x-3}-4$ do postaci ogólnej.

Rozwiązanie

Sprowadzamy wyrazy do wspólnego mianownika oraz wykonujemy działania:

$f\left(x\right)=\frac{5}{x-3}-4$

$f\left(x\right)=\frac{5}{x-3}-\frac{4\left(x-3\right)}{x-3}$

$f\left(x\right)=\frac{5-4x+12}{x-3}$

$f\left(x\right)=\frac{-4x+17}{x-3}$

Odpowiedź:

Postać ogólna funkcji $f$ to: $f\left(x\right)=\frac{-4x+17}{x-3}$

Naszkicujemy wykres funkcji $f\left(x\right)=\frac{-2x+4}{x-1}$ oraz omówimy jej własności.

Rozwiązanie

Najpierw przekształcimy wzór  funkcji do postaci kanonicznej:

$f\left(x\right)=\frac{-2x+4}{x-1}$

$f\left(x\right)=\frac{-2\left(x-1\right)+2}{x-1}$

$f\left(x\right)=-2+\frac{2}{x-1}$

Następnie rysujemy wykres funkcji $g\left(x\right)=\frac{2}{x}$ i przesuwamy go o wektor $\left[1,-2\right]$

R16r85SJOPH22

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus pięciu do siedmiu oraz pionową osią $Y$ od minus sześciu do czterech. Na płaszczyźnie narysowano wykres funkcji, który stanowi hiperbola. Asymptotę poziomą opisuje równanie $y=-2$, natomiast pionową $x=1$. Wykres funkcji przechodzi przez punkty $\left(2;0\right)$ oraz $\left(0;-4\right)$.

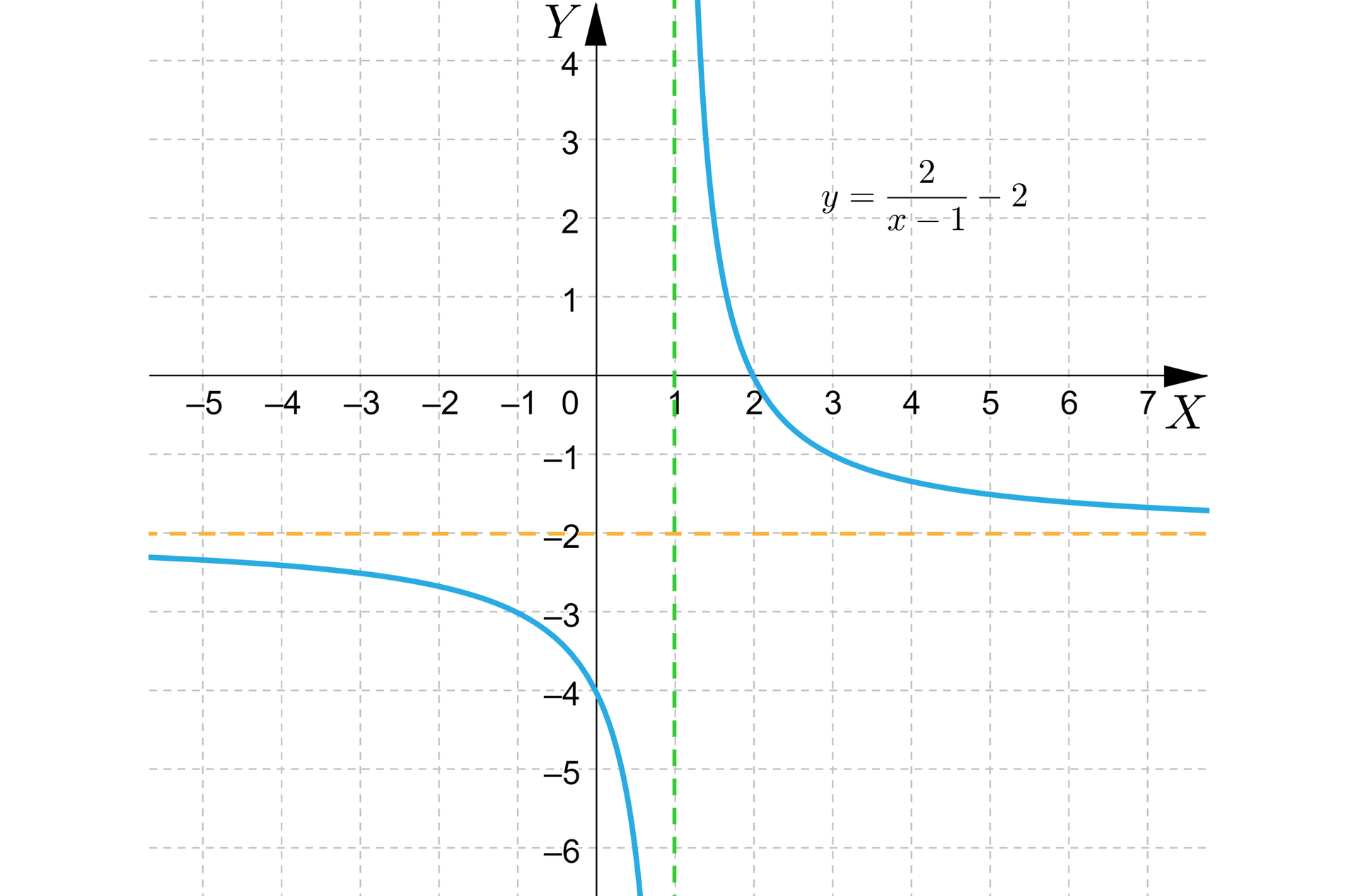
• Dziedzina funkcji: $D_f=\mathrm{ℝ}\setminus \left\{1\right\}$.

• Zbiór wartości funkcji: $Z{W}_f=\mathrm{ℝ}\setminus \left\{-2\right\}$.

• Miejsce zerowe: $x_0=2$.

• Wykres funkcji przecina oś $Y$ w punkcie $\left(0,-4\right)$.

• Funkcja jest malejąca w każdym z przedziałów: $\left(-\infty ,1\right)$, $\left(1,\infty \right)$.

• $f\left(x\right)>0$ dla $x\in \left(1,2\right)$.

• $f\left(x\right)<0$ dla $x\in \left(-\infty ,1\right)\cup \left(2,\infty \right)$.

• Funkcja jest różnowartościowa.

• Funkcja nie przyjmuje ani wartości najmniejszej, ani największej.

• Wykres funkcji jest symetryczny względem punktu $\left(1,-2\right)$.

• Wykres funkcji jest symetryczny względem prostych: $y=x-3$ oraz $y=-x-1$.

• Wykres funkcji ma asymptotę poziomą o równaniu: $y=-2$.

• Wykres funkcji ma asymptotę pionową o równaniu: $x=1$.

Obliczymy pole prostokąta, którego boki zawierają się w prostych będących asymptotami wykresu funkcji $f\left(x\right)=\frac{-2x-9}{x+4}$ oraz w osiach układu współrzędnych.

Rozwiązanie

Aby wyznaczyć równania asymptot, należy przekształcić wzór funkcji do postaci kanonicznej

$f\left(x\right)=\frac{-2x-9}{x+4}$

$f\left(x\right)=\frac{-2\left(x+4\right)-1}{x+4}$

$f\left(x\right)=-2-\frac{1}{x+4}$

Zatem asymptotami wykresu funkcji są proste o równaniach: $x=-4$, $y=-2$, które wraz z osiami układu współrzędnych ograniczają prostokąt o bokach $4$ oraz $2$ i polu równym $8$.

R1CXukWizSMUO

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus dziewięciu do trzech oraz pionową osią $Y$ od minus pięciu do czterech. Na płaszczyźnie narysowano wykres funkcji, który stanowi hiperbola o wierzchołkach w punktach $\left(-5;-1\right)$ oraz $\left(-3;-3\right)$. Asymptotę poziomą opisuje równanie y=-2, natomiast pionową x=-4. Zacieniowano prostokąt, którego wierzchołki stanowią punkty $A=\left(-4;-2\right)$, $B=\left(0;-2\right)$, $C=\left(0;0\right)$, $C=\left(-4;0\right)$.

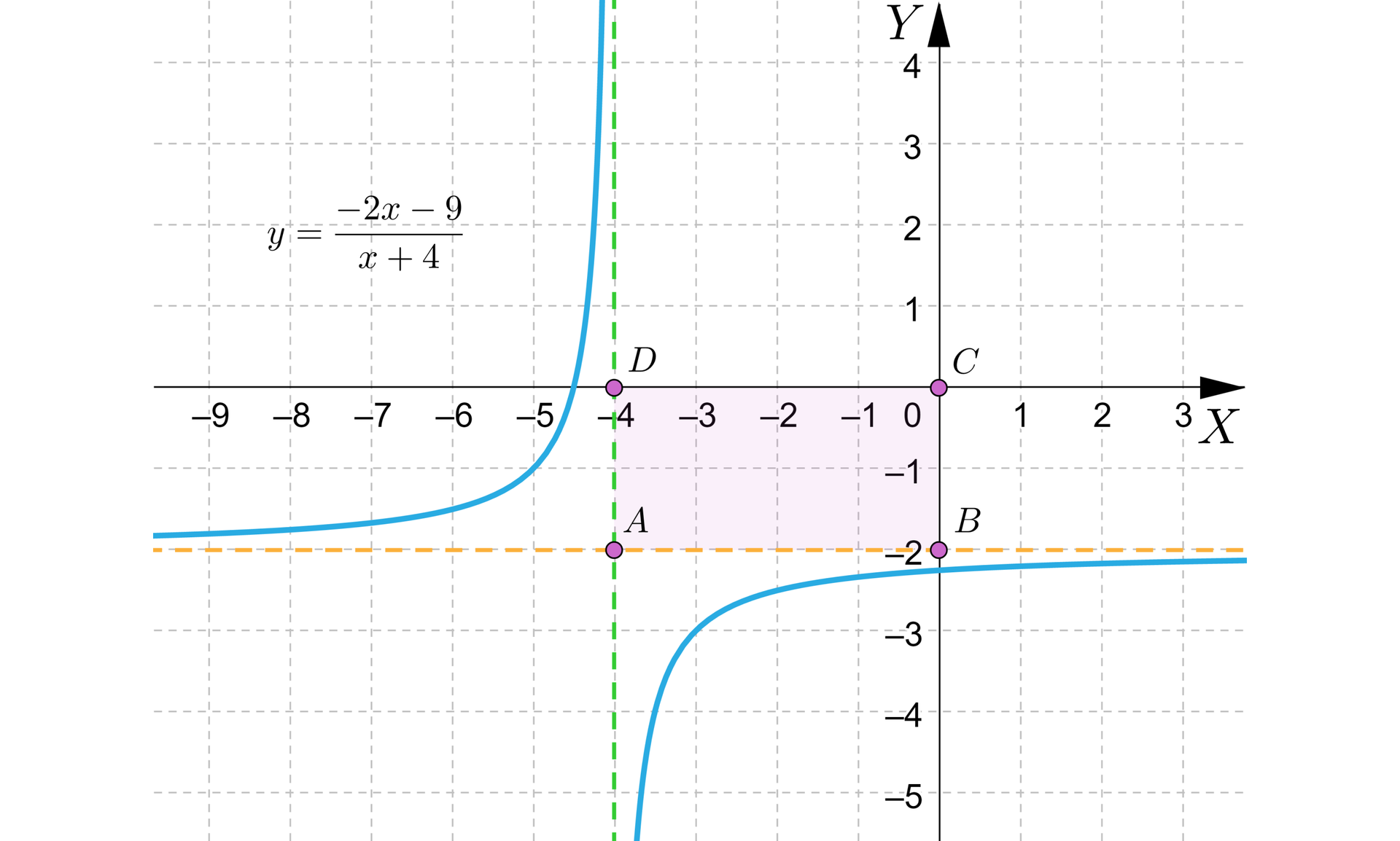
Wyznaczymy punkty należące do wykresu funkcji $f\left(x\right)=\frac{4x-10}{x-1}$, których obie współrzędne są liczbami naturalnymi.

Rozwiązanie

Najpierw przekształcimy wzór funkcji do postaci kanonicznej:

$f\left(x\right)=\frac{4x-10}{x-1}$

$f\left(x\right)=\frac{4\left(x-1\right)-6}{x-1}$

$f\left(x\right)=4-\frac{6}{x-1}$

Ponieważ $4$ jest liczbą naturalną, wartość funkcji $f\left(x\right)$ będzie liczbą naturalną, jeśli wyrażenie $\frac{6}{x-1}$ będzie liczbą całkowitą  $4$ oraz $x-1\ne 1$. Zatem $x-1$ musi być dzielnikiem liczby $6$, czyli:

$x-1=-6$

lub

$x-1=6$

lub

$x-1=-3$

lub

$x-1=3$

lub

$x-1=2$

lub

$x-1=-2$

lub

$x-1=1$

lub

x‑1=- 1

zatem $x\in \left\{7, 4, 3, -5, -2, -1, 0\right\}$ oraz $x\in \mathrm{\mathbb{N}}$ a także $f\left(x\right)\in \mathrm{\mathbb{N}}$.

Wszystkie warunki spełniają $x\in \left\{7, 4, 3, 0\right\}$

Odpowiedź:

Punkty o obu współrzędnych naturalnych należące do wykresu funkcji $f$, to: $\left(7,3\right)$, $\left(0,10\right)$, $\left(4,2\right)$, $\left(3,1\right)$.

Udowodnimy, że funkcja $f\left(x\right)=\frac{3x-2}{x-2}$, $x\ne 2$ jest malejąca w zbiorze $\left(2,\infty \right)$.

Rozwiązanie

Założenie:

$f\left(x\right)=\frac{3x-2}{x-2}$, $D_f=\mathrm{ℝ}\setminus \left\{2\right\}$, $x_1$, $x_2\in \left(2,\infty \right)$ i $x_1<x_2$

Teza:

$f\left(x_1\right)>f\left(x_2\right)$

Dowód:

Zbadamy znak różnicy wartości funkcji $f$ dla argumentów $x_1$, $x_2\in \left(2,\infty \right)$:

$f\left(x_1\right)-f\left(x_2\right)=\frac{3x_1-2}{x_1-2}-\frac{3x_2-2}{x_2-2}=\frac{\left(3x_1-2\right)\left(x_2-2\right)}{\left(x_1-2\right)\left(x_2-2\right)}-\frac{\left(3x_2-2\right)\left(x_1-2\right)}{\left(x_1-2\right)\left(x_2-2\right)}=$

$=\frac{3x_1{x}_2-6x_1-2x_2+4-3x_1{x}_2+2x_1+6x_2-4}{\left(x_1-2\right)\left(x_2-2\right)}=\frac{-4\left(x_1-x_2\right)}{\left(x_1-2\right)\left(x_2-2\right)}>0$

Uzasadnienie:

• $x_1-x_2<0$ z założenia, ponieważ $x_1<x_2$;

• $-4\left(x_1-x_2\right)>0$, ponieważ iloczyn dwóch liczb ujemnych jest liczbą dodatnią;

• $x_1-2>0$ z założenia, ponieważ $x_1>2$;

• $x_2-2>0$ z założenia, ponieważ $x_2>2$;

• $\left(x_1-2\right)\left(x_2-2\right)>0$, ponieważ iloczyn dwóch liczb dodatnich jest liczbą dodatnią;

• $\frac{-4\left(x_1-x_2\right)}{\left(x_1-2\right)\left(x_2-2\right)}>0$, ponieważ iloraz dwóch liczb dodatnich jest liczbą dodatnią.

Otrzymaliśmy nierówność $f\left(x_1\right)-f\left(x_2\right)>0$, zatem $f\left(x_1\right)>f\left(x_2\right)$, co należało udowodnić.

funkcja, która jest ilorazem dwóch wielomianów

prosta jest asymptotą danej krzywej, jeśli dla punktu oddalającego się nieograniczenie wzdłuż krzywej, odległość tego punktu od prostej dąży do zera; asymptota funkcji to asymptota krzywej stanowiącej wykres funkcji