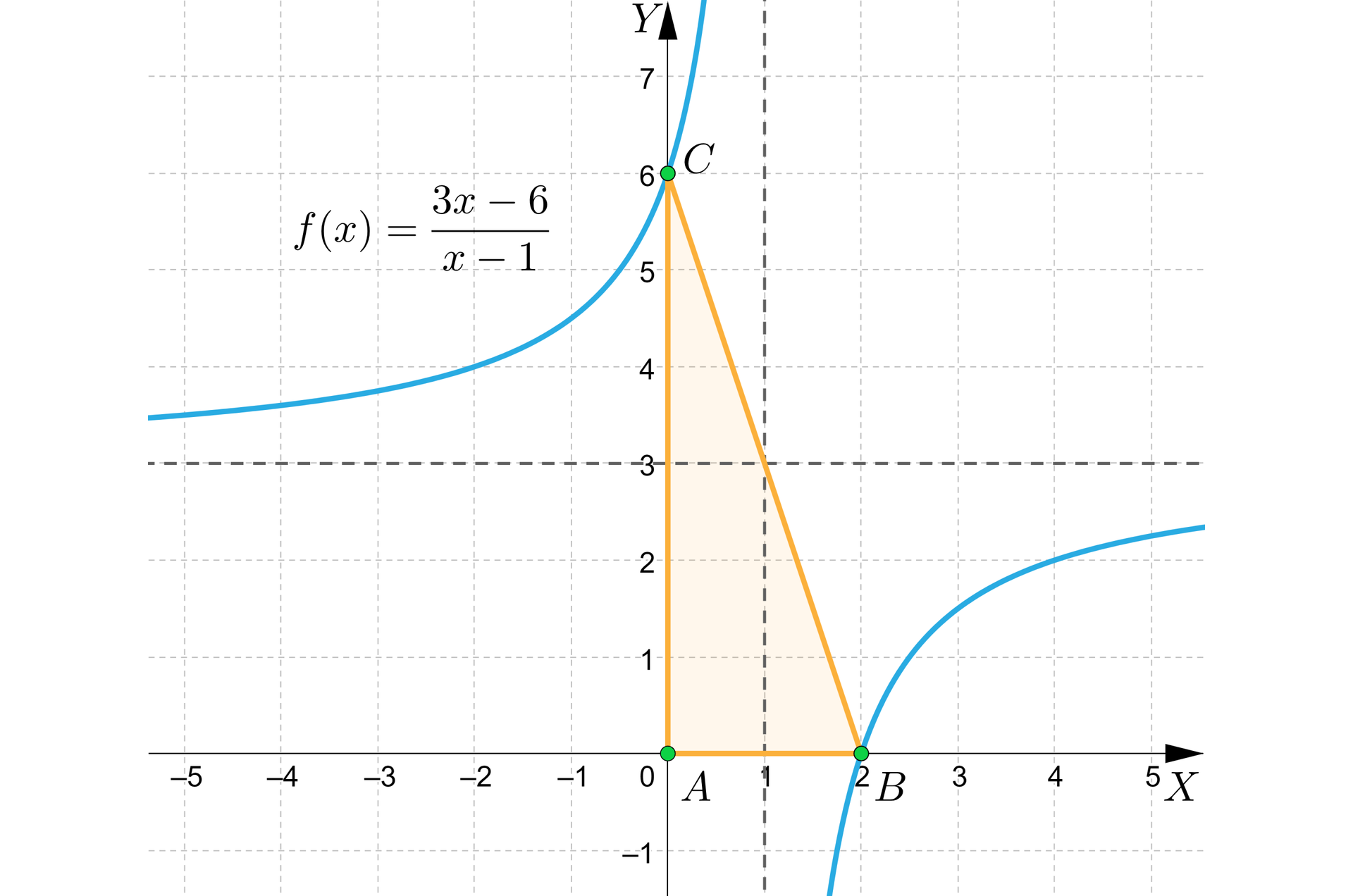Symulacja interaktywna
Polecenie 1
Funkcja homograficzna jest szczególnym przypadkiem funkcji wymiernej. Jej wykresem jest hiperbola. Zapoznaj się z symulacją interaktywną, która przedstawia wykres i własności hiperboli. Zmieniając współczynniki , , i obserwuj, jak zmienia się wykres funkcji homograficznej.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHw5bGANi
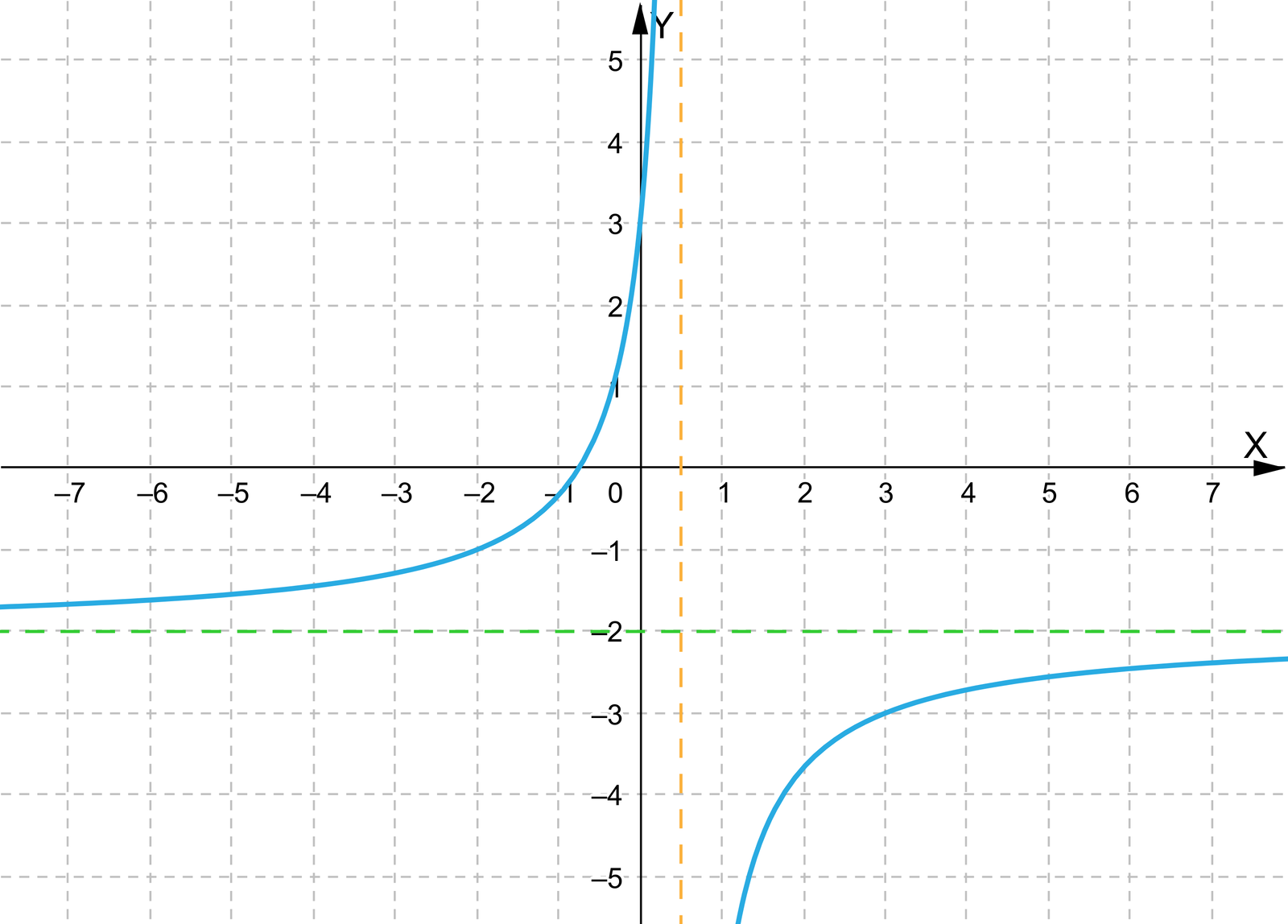
Polecenie 2
Narysuj wykres funkcji , opisz jej własności, a następnie korzystając z symulacji z Polecenia 1 sprawdź swoją odpowiedź.
Opisz jak narysować wykres funkcji .
Polecenie 3
Pole trójkąta, którego wierzchołkami są: początek układu współrzędnych oraz punkty przecięcia wykresu funkcji z osiami układu współrzędnych wynosi .............
Polecenie 4
Odpowiedz na pytania lub uzupełnij tekst. 1. Wzór , , to postać ogólna funkcji ...., 2. Wzór to postać .... funkcji homograficznej., 3. Prosta to ... wykresu funkcji , 4. Punkt jest ... symetrii wykresu funkcji , 5. Proste , są osiami .... wykresu funkcji , 6. jjj, 7. Zbiór to zbiór ..... funkcji , 8. Funkcja jest .... w każdym z przedziałów , , 9. Zbiór to .... funkcji
Rozwiąż krzyżówkę:
- Wzór , , to postać ogólna funkcji ...
- Wzór to postać ... funkcji homograficznej.
- Prosta to ... wykresu funkcji .
- Punkt jest ... symetrii wykresu funkcji .
- Proste , są osiami ... wykresu funkcji .
- Krzywa będąca wykresem funkcji homograficznej to ...
- Zbiór to zbiór ... funkcji .
- Funkcja jest ... w każdym z przedziałów , .
- Zbiór to ... funkcji .
| 1 | ||||||||||||||||||||||
| 2 | ||||||||||||||||||||||
| 3 | ||||||||||||||||||||||
| 4 | ||||||||||||||||||||||
| 5 | ||||||||||||||||||||||
| 6 | ||||||||||||||||||||||
| 7 | ||||||||||||||||||||||
| 8 | ||||||||||||||||||||||
| 9 |