Przeczytaj
Prosta jest asymptotą danej krzywej, jeśli dla punktu oddalającego się nieograniczenie wzdłuż krzywej odległość tego punktu od prostej dąży do zera. Asymptota funkcji to asymptota krzywej stanowiącej wykres funkcji.
Poniższy rysunek przedstawia wykres funkcji .
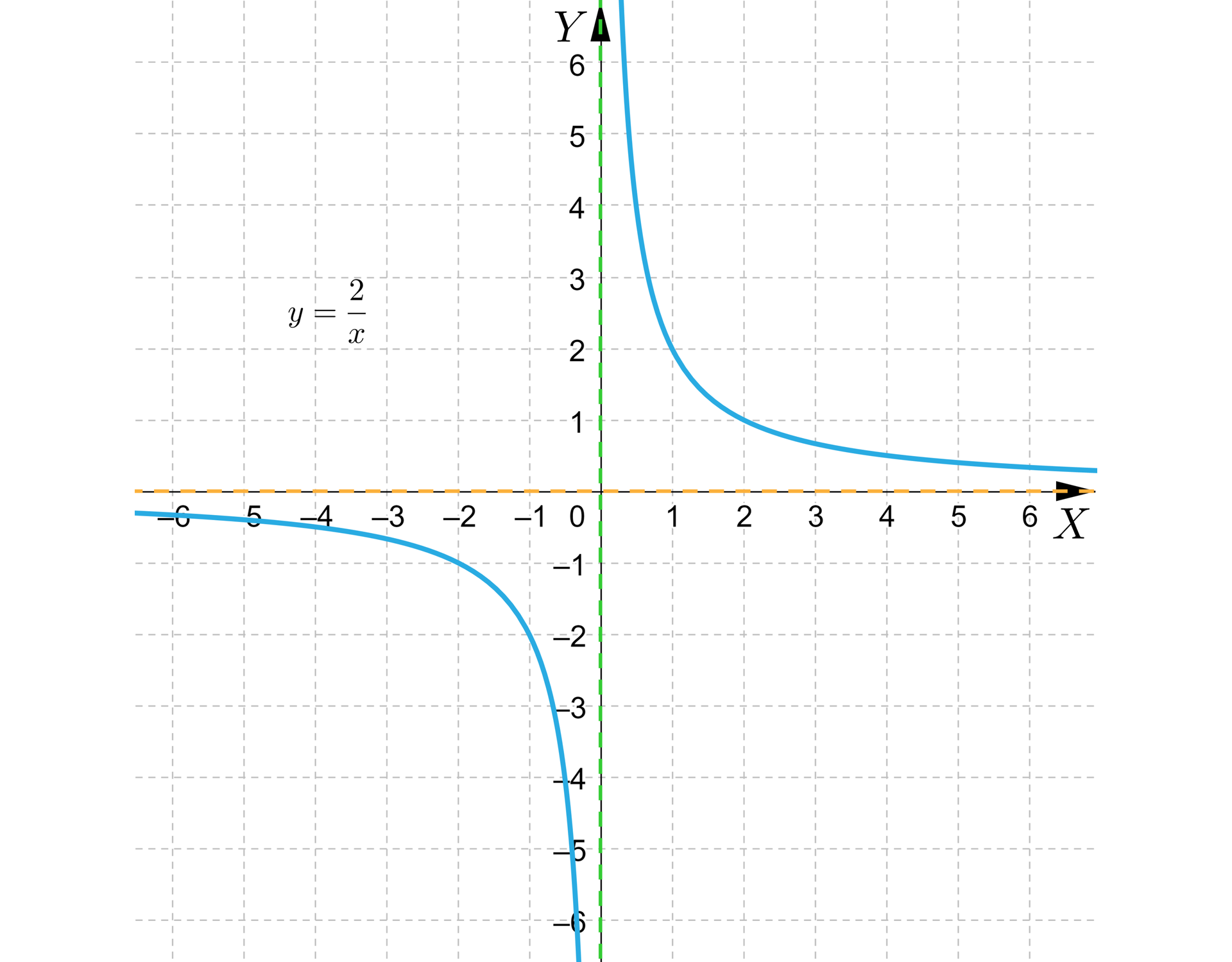
Wyznaczymy równania asymptot.
Rozwiązanie
Wykres funkcji posiada dwie asymptoty: pionową – o równaniu (zielona przerywana linia) oraz poziomą – o równaniu (pomarańczowa przerywana linia).
Wykres każdej funkcji postaci , dla i posiada dwie asymptoty – pionową o równaniu , oraz poziomą o równaniu .
Zauważmy, że funkcja nie jest określona dla i właśnie prosta o równaniu jest asymptotą pionową. Podobnie funkcja nie przyjmuje wartości i prosta jest asymptotą poziomą.
Wyznaczymy równania asymptot wykresu funkcji .
Rozwiązanie
Wykres funkcji powstaje w wyniku translacjitranslacji wykresu funkcji o wektor . Przesunięciu ulegają również asymptoty.
Równanie asymptoty pionowej: .
Równanie asymptoty poziomej: .
Poniższy rysunek przedstawia opisaną sytuację.
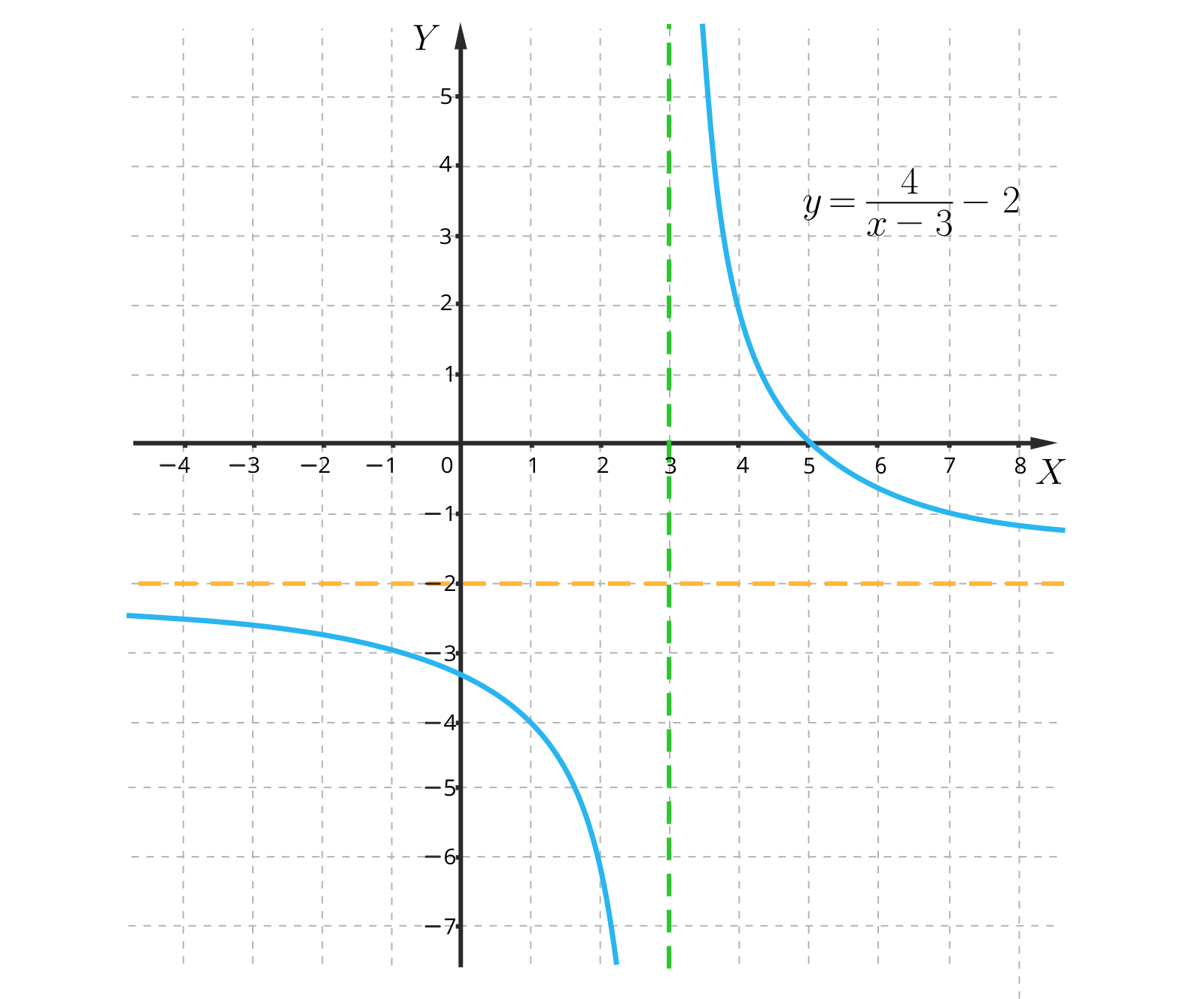
Zauważmy, że wraz z przesunięciem asymptot zmianie uległa dziedzina i zbiór wartości funkcji.
Asymptotami wykresu funkcji są proste o równaniach:
– asymptota pionowa,
– asymptota pozioma.
Zauważmy, że funkcja nie jest określona dla i właśnie prosta o równaniu jest asymptotą pionową. Podobnie funkcja nie przyjmuje wartości i prosta jest asymptotą poziomą.
Wyznaczymy równania asymptot wykresu funkcji na podstawie jej wykresu.
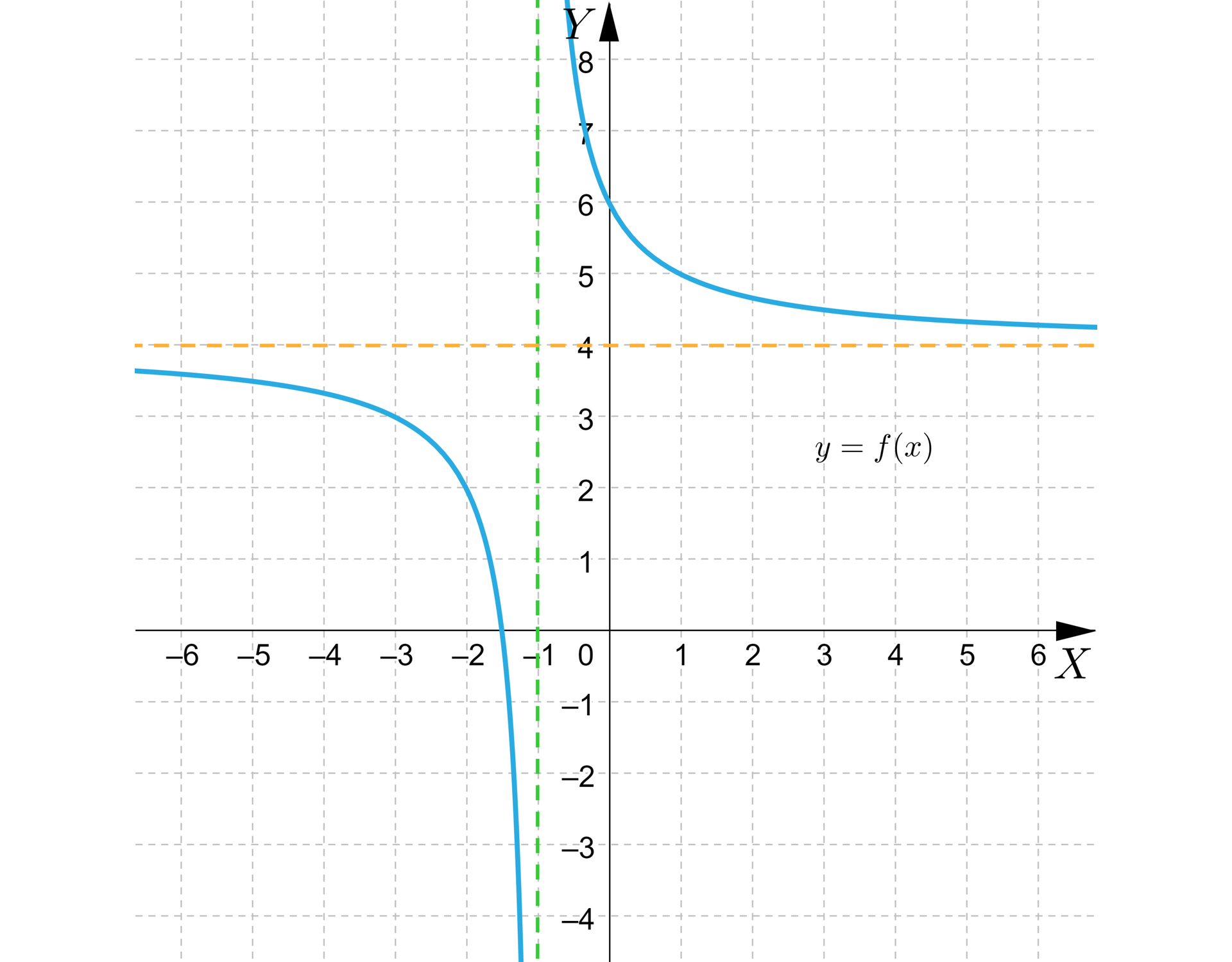
Rozwiązanie
Równanie asymptoty pionowej: .
Równanie asymptoty poziomej: .
Wyznaczymy równania asymptot wykresu funkcji .
Rozwiązanie
Zgodnie z regułą 2:
równanie asymptoty pionowej: ,
równanie asymptoty poziomej: .
Wyznaczymy równania asymptot wykresu funkcji .
Rozwiązanie
Aby wyznaczyć asymptoty wykresu funkcji należy wzór funkcji przekształcić do postaci kanonicznej:
.
Równanie asymptoty pionowej: .
Równanie asymptoty poziomej: .
Słownik
przesunięcie równoległe