Przeczytaj
WEKTOR JAKO PRZEMIESZCZENIE
Jedną z podstawowych wielkości fizycznych jest przemieszczenieprzemieszczenie, czyli wektor o początku w punkcie będącym położeniem początkowym ciała i końcu w punkcie będącym położeniem końcowym.
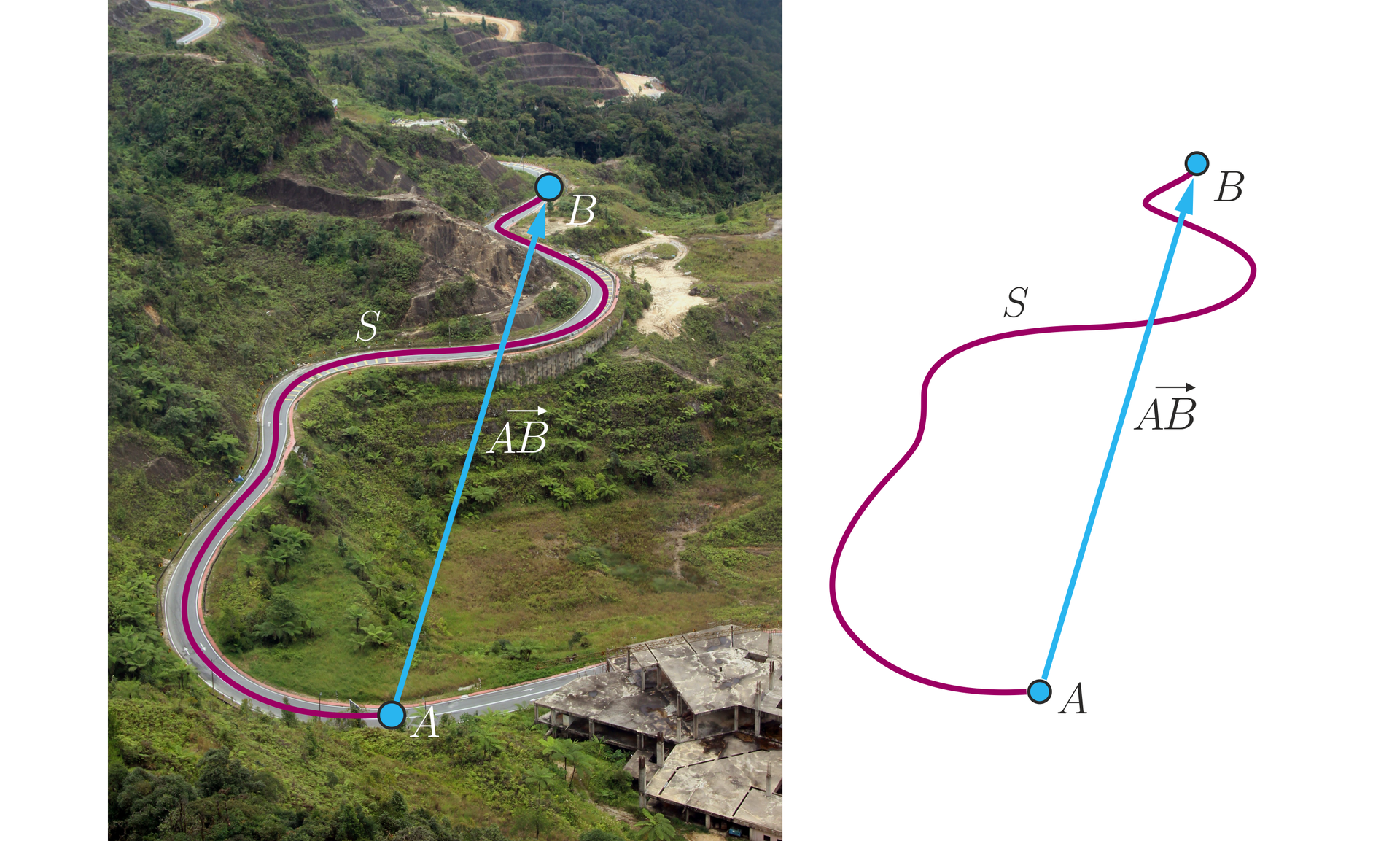
Jeżeli wektor przemieszczenia ma tę samą długość co tor ruchu, to taki ruch nazywamy ruchem prostoliniowymruchem prostoliniowym. W przypadku ruchu krzywoliniowegoruchu krzywoliniowego długość toru ruchu jest większa niż długość wektora przemieszczenia.
Przemieszczenie opisane jako “ metrów” możemy utożsamić z wektorem na osi o współrzędnej [], jeśli przemieszczenie nastąpiło w stronę, w którą liczby rosną (zwyczajowo w prawo), lub [], jeśli przemieszczenieprzemieszczenie nastąpiło w stronę, w która liczby maleją (zwyczajowo w lewo). W obu przypadkach długość wektora przemieszczenia jest równa .
WEKTOR POŁOŻENIA
Jeśli na płaszczyźnie wyróżnimy jeden punkt, nazwijmy go , to położenie wszystkich pozostałych punktów możemy określać względem tego wyróżnionego punktu. To znaczy: wektor o początku w punkcie i końcu w punkcie () nazywamy wektorem położenia lub wektorem wodzącym punktu . Jeżeli punkt zmienia swoje położenie względem wyróżnionego punktu, dochodzi jednocześnie do zmiany wektora położenia. Na rysunku poniżej obiekt znajdujący się w punkcie przemieścił się do punktu . Jeśli przez oznaczymy wektor położenia punktu , przez wektor położenia punktu , zaś przez wektor , wówczas , czyli . Wektor nazywamy zmianą wektora położenia.

PRĘDKOŚĆ WEKTOROWA
Prędkość wektorową średnią ( ) definiujemy jako iloraz zmiany wektora położenia () do czasu (), w jakim ta zmiana nastąpiła.
Długość wektora opisującego prędkość nazywamy szybkością.
Obliczymy średnią prędkość wektorową, jeśli ciało porusza się z punktu do punktu w czasie .
Obliczmy współrzędne zmiany wektora położenia .
Ponieważ średnia prędkość wektorowa to iloraz zmiany wektora przemieszczenia przez czas, w którym ta zmiana zachodzi otrzymujemy . Zatem średnia prędkość wektorowa ma współrzędne .
PRZYSPIESZENIE JAKO WEKTOR
Przyspieszenie średnie (ozn. ) definiujemy jako stosunek zmiany wektora prędkości (ozn. ) do czasu (ozn. ), w jakim ta zmiana nastąpiła.
.
SIŁA JAKO WEKTOR
W mechanice klasycznej siłę (ozn. ) można zdefiniować jako iloczyn masy ( ozn. ) i przyspieszenia (ozn. ):
Obliczymy współrzędne wektora siły, która ciału o masie nadaje przyspieszenie opisujące się wektorem o współrzędnych .
Ponieważ siła jest iloczynem masy i wektora przyspieszenia, więc . Zatem opisana siła ma współrzędne .
PRACA JAKO ILOCZYN SKALARNY WEKTORÓW
Ogólnie praca to miara ilości energii przekazywanej między układami. Jeżeli ruch ciała jest prostoliniowy a wektor siły () jest stały, pracę (W) tej siły określa wzór , gdzie jest wektorem przemieszczenia, zaś jest kątem między wektorem siły a wektorem przemieszczenia. W lekcji o temacie “Działania na wektorach w układzie współrzędnych” opisaliśmy szczegółowo zagadnienie iloczynu skalarnego, który pojawia się w tym wzorze.
Obliczymy pracę wykonaną nad ciałem, które przemieściło się z punktu do punktu pod wpływem siły o współrzędnych .
Wektor przemieszczenia ma współrzędne . Zatem praca wykonana pod wpływem tej siły ma wartość .
Słownik
wektor o początku w punkcie będącym położeniem początkowym ciała i końcu w punkcie będącym położeniem końcowym
jeżeli wektor przemieszczenia ma tę samą długość co tor ruchu, to taki ruch nazywamy ruchem prostoliniowym; jeśli długość toru ruchu jest większa niż długość wektora przemieszczenia, mówimy o ruchu krzywoliniowym