Średnią arytmetyczną kilku liczb nazywamy sumę tych  liczb podzieloną przez ich liczbę. Dla dwóch liczb $a$ i $b$ średnia arytmetyczna jest równa: $s_a=\frac{a+b}{2}$.

Średnią geometryczną $n$ dodatnich liczb nazywamy pierwiastek $n$-tego stopnia z iloczynu tych liczb. Dla dwóch liczb dodatnich $a$ i $b$ średnia geometryczna jest równa: $s_g=\sqrt{ab}$.

Średnią harmoniczną $n$ dodatnich liczb nazywamy odwrotność średniej arytmetycznej odwrotności tych liczb. Dla dwóch liczb dodatnich $a$ i $b$ średnia harmoniczna jest równa: $s_h=\frac{2}{\frac{1}{a}+\frac{1}{b}}$. Wzór ten często występuje w prostszej postaci: $s_h=\frac{2ab}{a+b}$.

W dowolnym trapezie długość odcinka łączącego środki boków nierównoległych jest równa średniej arytmetycznej długości podstaw tego trapezu.

W dowolnym trapezie długość odcinka równoległego do podstaw trapezu i dzielącego ten trapez na dwa trapezy podobne jest równa średniej geometrycznej długości podstaw tego trapezu.

W dowolnym trapezie długość odcinka równoległego do podstaw i przechodzącego przez punkt przecięcia przekątnych trapezu jest równa średniej harmonicznej długości podstaw tego trapezu.

Udowodnij, że dla dowolnych liczb dodatnich $a$ i $b$ prawdziwa jest nierówność: $S_h\le S_g\le S_a$.

Udowodnimy koniunkcję nierówności:

1. $\frac{2ab}{a+b}\le \sqrt{ab} \wedge$ 2. $\sqrt{ab}\le \frac{a+b}{2}$

Założenie 1

koniunkcjakoniunkcja $a>0\wedge b>0$ (koniunkcjakoniunkcjakoniunkcja dwóch zdań logicznych)

Teza 1

$\frac{2ab}{a+b}\le \sqrt{ab}$

Dowód 1

Utwórzmy kwadrat różnicy liczb $a$ i $b$: ${\left(a-b\right)}^2$.

Wiadomo, że dla dowolnych liczb $a$ i $b$ jest on nieujemny: ${\left(a-b\right)}^2\ge 0$.

Po zastosowaniu wzoru skróconego mnożenia otrzymujemy: $a^2-2ab+b^2\ge 0$.

Wykonujemy przekształcenia równoważne:

$a^2-2ab+b^2\ge 0 |+2ab$

$a^2+b^2\ge 2ab |+2ab$

$a^2+2ab+b^2\ge 4ab$

${\left(a+b\right)}^2\ge 4ab |\cdot ab$

$ab{\left(a+b\right)}^2\ge 4a^2{b}^2 |:{\left(a+b\right)}^2$.

Powyższą nierówność możemy podzielić przez ${\left(a+b\right)}^2$, ponieważ dla dowolonych liczb dodatnich $a$ i $b$ wyrażenie ${\left(a+b\right)}^2>0$.

$ab\ge \frac{4a^2{b}^2}{{\left(a+b\right)}^2}$

Ponieważ $ab>0$ oraz $\frac{4a^2{b}^2}{{\left(a+b\right)}^2}>0$, to możemy spierwiastkować obie strony nierówności.

$\sqrt{ab}\ge \frac{2ab}{a+b}$

Zatem: $\frac{2ab}{a+b}\le \sqrt{ab}\iff S_h\le S_g$

Założenie 2

$a>0\wedge b>0$

Teza 2

$\sqrt{ab}\le \frac{a+b}{2}$

Dowód 2

Ponieważ liczby $a$ oraz $b$ są nieujemne, więc istnieją pierwiastki $\sqrt{a}$ oraz $\sqrt{b}$.

Utwórzmy kwadrat różnicy tych pierwiastków: ${\left(\sqrt{a}-\sqrt{b}\right)}^2$.

Wiadomo o nim, że jest nieujemny: ${\left(\sqrt{a}-\sqrt{b}\right)}^2\ge 0$.

Po zastosowaniu wzoru skróconego mnożenia otrzymujemy: $a-2\sqrt{ab}+b\ge 0$.

Wykonujemy przekształcenia równoważne:

$a-2\sqrt{ab}+b\ge 0 |+2\sqrt{ab}$

$a+b\ge 2\sqrt{ab} |:2$

$\frac{a+b}{2}\ge \sqrt{ab}$

Zatem: $\sqrt{ab}\le \frac{a+b}{2}\iff S_g\le S_a$

Podsumowując obie tezy otrzymujemy nierówność podwójną: $S_h\le S_g\le S_a$, co było do udowodnienia.

Zapoznaj się także z geometrycznym sposobem uzasadnienia drugiej części tezy omówionego twierdzenia.

Geometryczny dowód Tezy 2

$\sqrt{ab}\le \frac{a+b}{2}$

Przyjmijmy, że $a$ oraz $b$ są długościami dwóch odcinków, np.

R1Y3Cyjh6cCRt

Ilustracja przedstawia dwa odcinki. Jeden o długości a, a drugi dłuższy o długości b.

Jeśli narysujemy okrąg o środku w punkcie $O$ i średnicy $a+b$, wówczas liczba $\frac{a+b}{2}$ jest promieniem tego okręgu, a jednocześnie średnią arytmetyczną liczb $a$ oraz $b$.

R1NQEs6RmTRFv

Ilustracja przedstawia dwa odcinki. Jeden o długości a, a drugi dłuższy o długości b. Połączono je. Tworzą one średnicę okręgu o środku O. Promień okręgu to $\frac{a+b}{2}$.

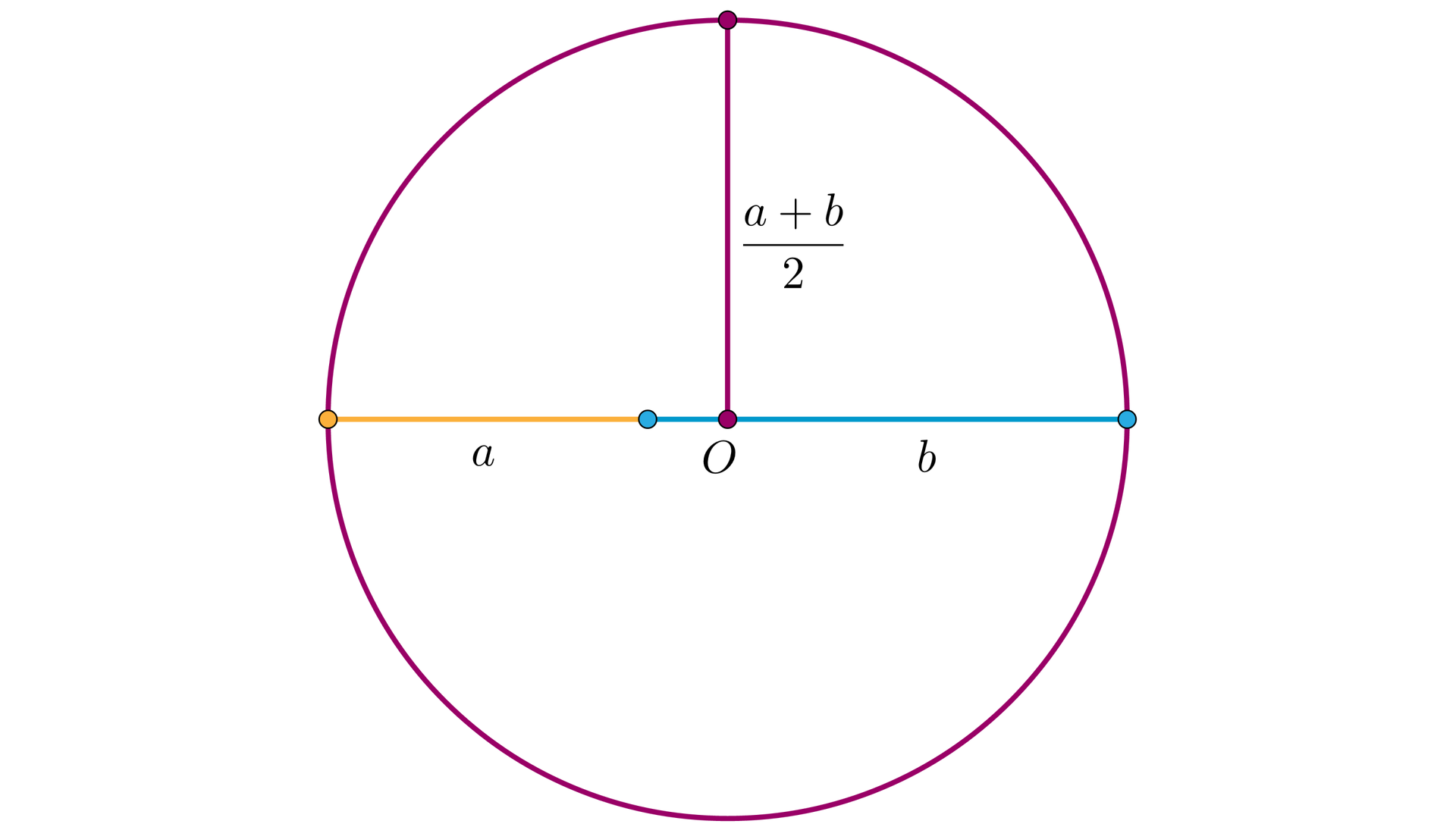
Narysujmy odcinek prostopadły do średnicy i przechodzący przez punkt $D$, a punkt wspólny tego odcinka z okręgiem oznaczmy przez $C$. Punkty wspólne okręgu z odcinkami $a$ oraz $b$ oznaczmy odpowiednio przez $A$ oraz $B$.

Otrzymany w ten sposób trójkąt $ABC$ jest trójkątem prostokątnym, na mocy twierdzenia o kącie wpisanym w okrąg opartym na półokręgu, a odcinek $CD$ jest wysokością tego trójkąta wychodzącą z wierzchołka kąta prostego.

R1KXh3s0YBGd2

Ilustracja przedstawia dwa odcinki. Jeden o długości a, a drugi dłuższy o długości b. Połączono je i oznaczono ich końce: odcinek a to odcinek A D, odcinek b to odcinek D B. Tworzą one średnicę okręgu o środku O. Promień okręgu to $\frac{a+b}{2}$. Odcinek AB jest średnicą okręgu jest on również podstawą trójkąta prostokątnego ABC wpisanego w okrąg. Zaznaczono jego wysokość C D o długości h.

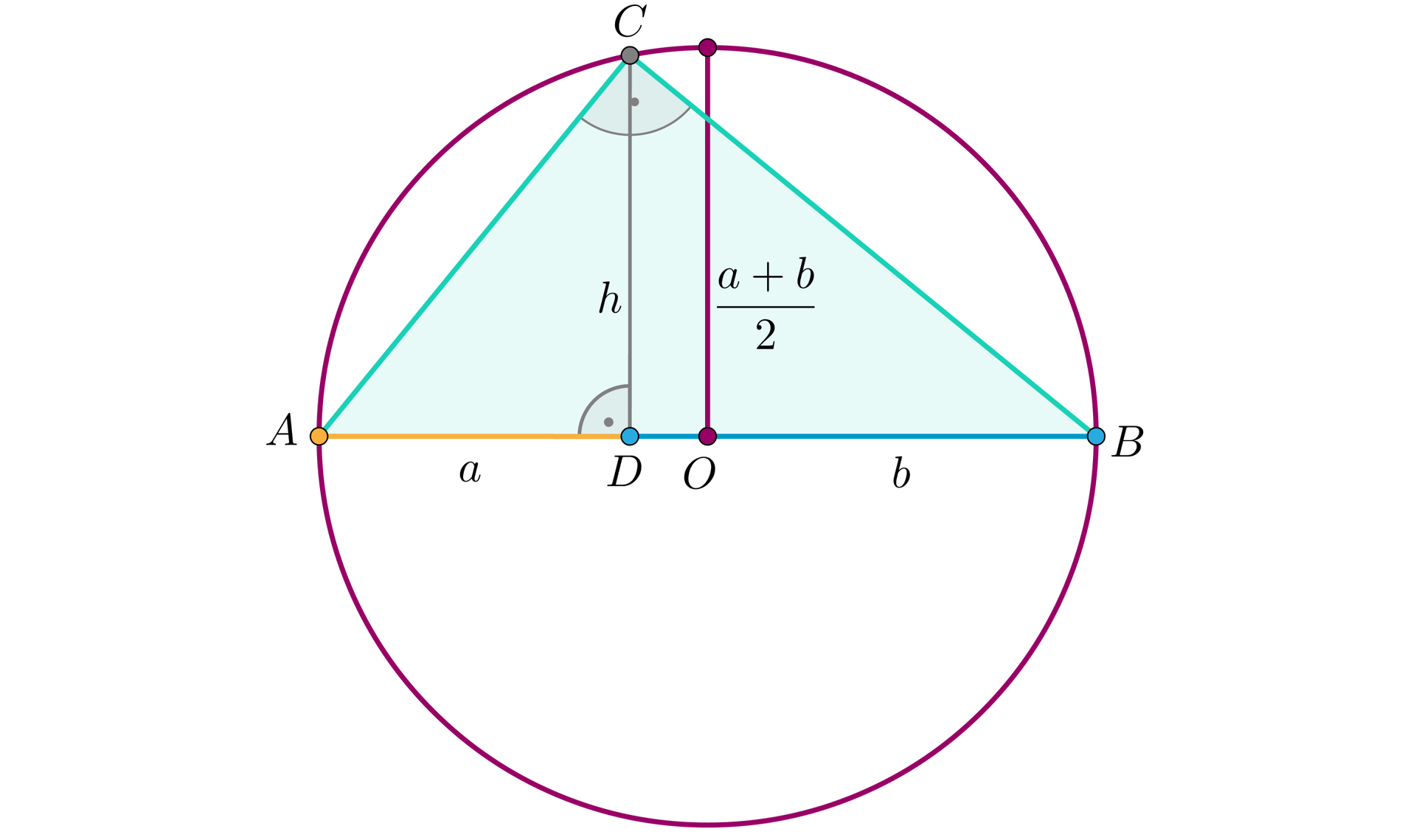
Podział trójkąta $ABC$ wysokością $CD$ pozwala zauważyć, że trójkąty $ACD$ oraz $BCD$ są podobne na mocy cechy podobieństwa trójkątów kąt‑kąt‑kąt (kkk). Stąd prawdziwa jest następująca proporcja: $\frac{a}{h}=\frac{h}{b}$.

Po przekształceniu tej proporcji dostaniemy: $h^2=ab\iff h=\sqrt{ab}$.

Wynika stąd, że odcinek $CD$ ma długość będącą średnią geometryczną długości odcinków $a$ oraz $b$.

Przy założeniu, że $a\ne b$ odcinek $CD$ jest zawsze krótszy od promienia okręgu, tzn. $\sqrt{ab}<\frac{a+b}{2}$.

R1UtWBfewYBkd

Ilustracja przedstawia dwa odcinki. Jeden o długości a, a drugi dłuższy o długości b. Połączono je i oznaczono ich końce: odcinek a to odcinek A D, odcinek b to odcinek D B. Tworzą one średnicę okręgu o środku O. Promień okręgu to $\frac{a+b}{2}$. Odcinek AB jest średnicą okręgu jest on również podstawą trójkąta prostokątnego ABC wpisanego w okrąg. Zaznaczono jego wysokość C D o długości h. Wysokość podzieliła trójkąt na dwa mniejsze trójkąty. Pierwszy ADC o kątach wewnętrznych alfa przy wierzchołku A, 90 stopni przy wierzchołku D oraz 90 stopni minus alfa przy wierzchołku C. Drugi BDC o kącie przy wierzchołku B równym 90 stopni minus alfa, przy wierzchołku D równym 90 stopni oraz przy wierzchołku C równym alfa.

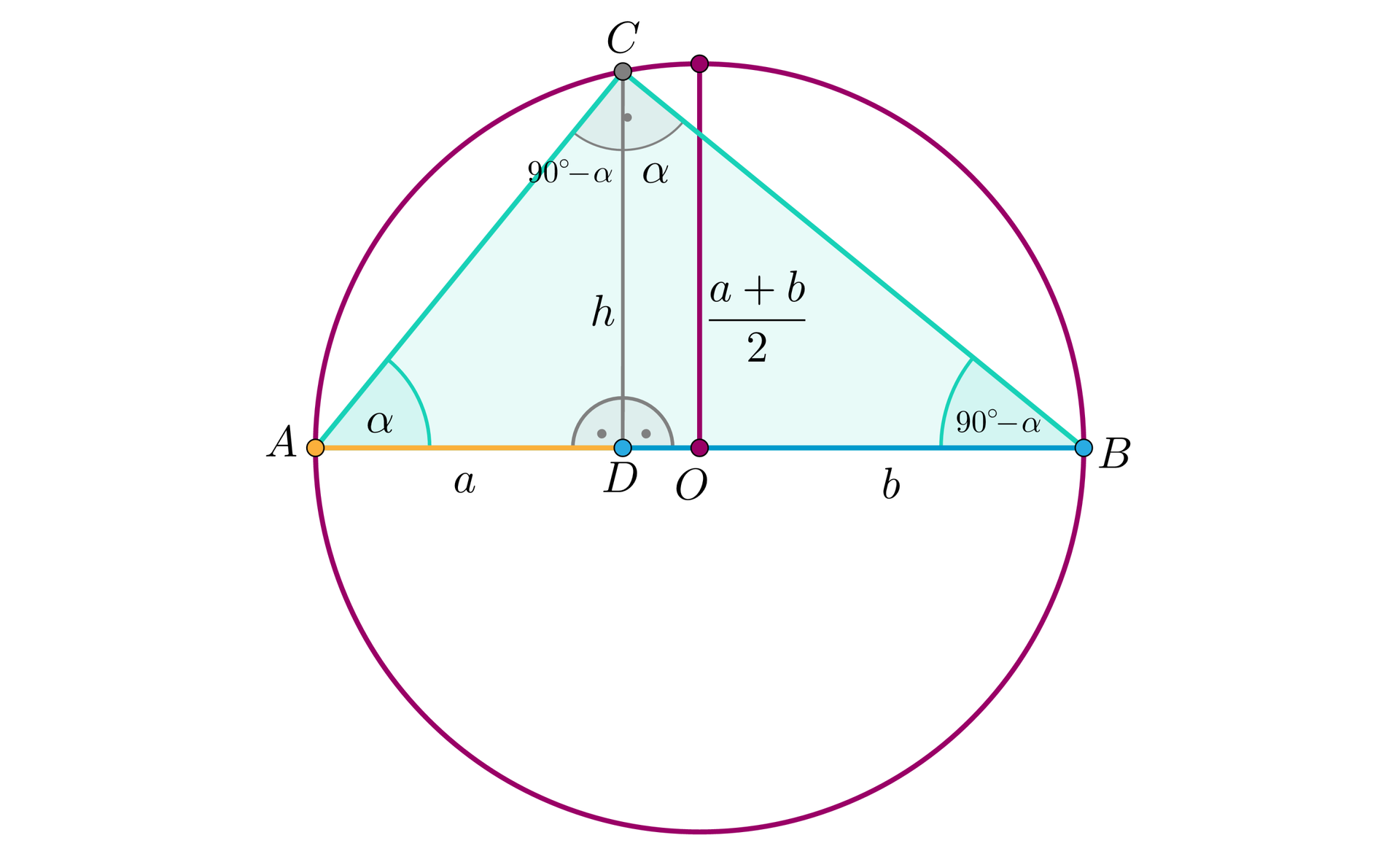
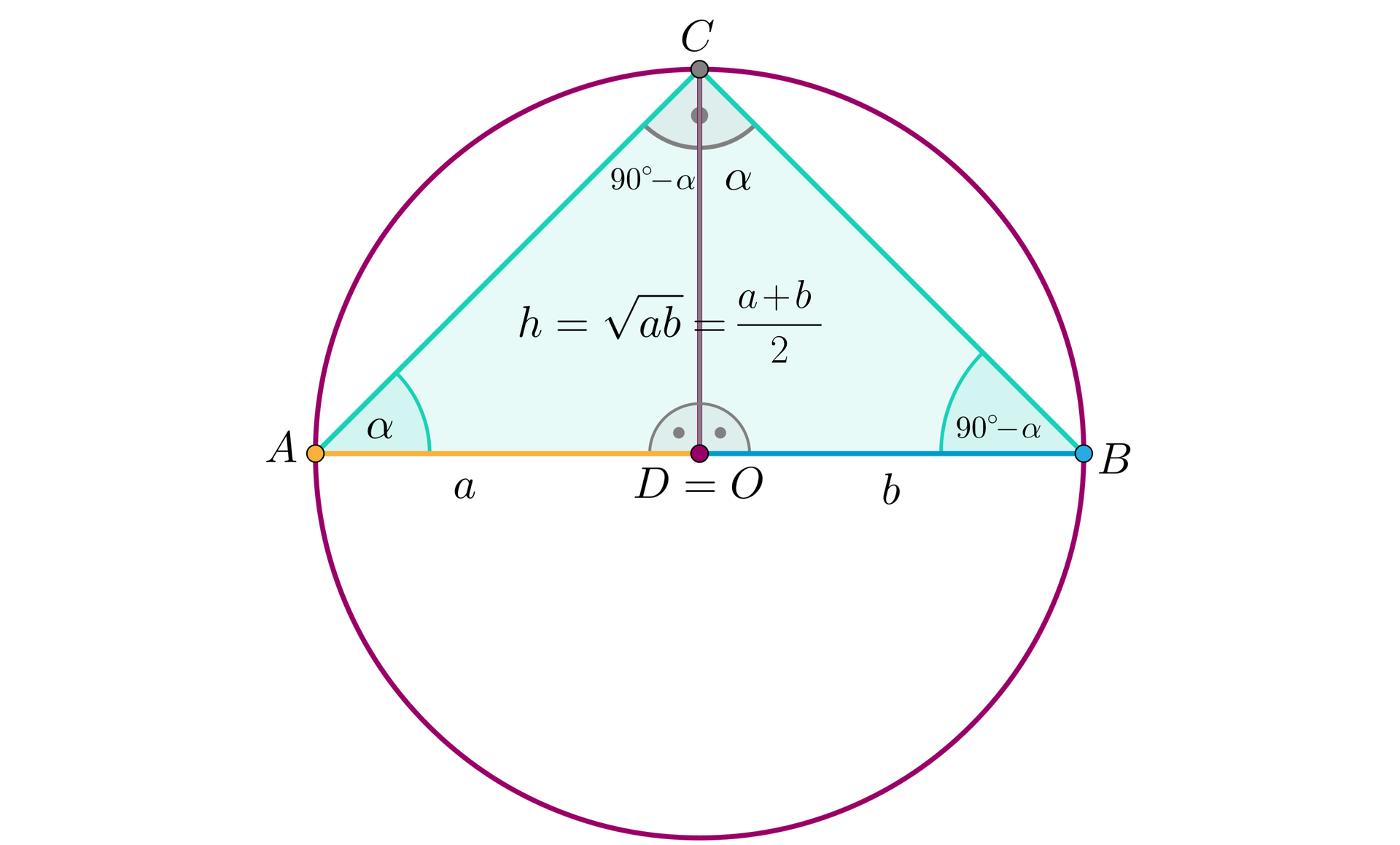
Natomiast w szczególności, gdy $a=b$ otrzymamy równość: $\sqrt{ab}=\frac{a+b}{2}$.

Podsumowując, wykazaliśmy, że dla dowolnych dodatnich liczb $a$ oraz $b$ zachodzi nierówność: $\sqrt{ab}\le \frac{a+b}{2}$.

RMo9hmXZP5A12

Ilustracja przedstawia równoramienny trójkąt prostokątny A B C wpisany w okrąg. Podstawa trójkąta składa się z odcinków AD o długości a oraz D B o długości b, gdzie punkt D pokrywa się ze środkiem okręgu O. Promień okręgu C D to $h=\sqrt{ab}=\frac{a+b}{2}$. Wysokość podzieliła trójkąt na dwa mniejsze. Pierwszy ADC o kątach wewnętrznych alfa przy wierzchołku A, 90 stopni przy wierzchołku D oraz 90 stopni minus alfa przy wierzchołku C. Drugi BDC o kącie przy wierzchołku B równym 90 stopni minus alfa, przy wierzchołku D równym 90 stopni oraz przy wierzchołku C równym alfa. Przesunięto wysokość CD tak, aby była równa promieniowi okręgu. Odcinki a i b są równe. Wysokość ma długość $\sqrt{ab}$

Pewien właściciel uprawy tulipanów, mający w swojej ofercie trzy gatunki tych kwiatów, ustalił następujące ceny sprzedaży:

• gatunek $\text{I}$ – $4,50 \mathrm{zł}$ za sztukę,

• gatunek $\text{II}$ – $3,00 \mathrm{zł}$ za sztukę,

• gatunek $\text{III}$ – $1,50 \mathrm{zł}$ za sztukę.

Na podstawie analizy zamówień wie, że w bieżącym miesiącu uzyska ze sprzedaży tulipanów następujące przychody: $9000 \mathrm{zł}$ za produkty w gatunku $\text{I}$ oraz $6000 \mathrm{zł}$ za produkty gatunku $\text{II}$. Ile sztuk tulipanów gatunku $\text{III}$ musiałby sprzedać, aby uzyskać średnią cenę sprzedaży między $3 \mathrm{zł}$, a $3,50 \mathrm{zł}$ za sztukę?

Średnią cenę sprzedaży $1$ sztuki produktu należy obliczyć jako stosunek uzyskanej ze sprzedaży łącznej kwoty pieniędzy [zł], do łącznej ilości sprzedanych produktów [szt.]. Jeśli więc przyjmiemy, że $x$ będzie oznaczać kwotę ze sprzedaży tulipanów $\text{III}$ gatunku, to warunki zadania spełniają liczby ze zbioru rozwiązań nierówności:

$3\le \frac{9000+6000+x}{\frac{9000}{4,5}+\frac{6000}{3}+\frac{x}{1,5}}\le 3,5$.

Do zapisu tej nierówności wykorzystane zostało pojęcie średniej harmonicznej ważonejśrednia harmoniczna ważonaśredniej harmonicznej ważonej.

Wykonujemy przekształcenia algebraiczne prowadzące do najprostszej postaci:

$3\le \frac{15000+x}{2000+2000+\frac{x}{1,5}}\le 3,5$

$3\le \frac{15000+x}{4000+\frac{x}{1,5}}\le 3,5$

$3\le \frac{15000+x}{\frac{6000+x}{1,5}}\le 3,5$

$3\le \frac{1,5\left(15000+x\right)}{6000+x}\le 3,5$

$3\le \frac{1,5x+22500}{6000+x}\le 3,5$.

Zauważmy, że mianownik $\left(6000+x\right)$ jest wyrażeniem dodatnim dla każdego dodatniego $x$, zatem pomnożymy nierówność podwójną przez ten mianownik i zachowamy zwrot nierówności:

$3\left(6000+x\right)\le 1,5x+22500\le 3,5\left(6000+x\right)$

$18000+3x\le 1,5x+22500\le 21000+3,5x$

$18000+3x\le 1,5x+22500 \wedge 1,5x+22500\le 21000+3,5x$

$3x-1,5x\le 22500-18000 \wedge 3,5x-1,5x\ge 22500-21000$

$1,5x\le 4500 |:1,5\wedge 2x\ge 1500 |:2$

$x\le 3000 \wedge x\ge 750$

Zatem kwota ze sprzedaży tulipanów $\text{III}$ gatunku powinna być nie mniejsza niż $750 \mathrm{zł}$, ale nie większa niż $3000 \mathrm{zł}$. Wiedząc, że cena tulipana w tym gatunku to $1,50 \mathrm{zł}$ za sztukę, obliczamy liczbę sztuk właściwą dla uzyskania żądanej średniej ceny:

$750:1,50=500$ oraz $3000:1,50=2000$

Odpowiedź: Właściciel powinien sprzedać nie mniej niż $500$ i nie więcej niż $2000$ sztuk tulipanów $\text{III}$ gatunku, aby osiągnąć średnią cenę za sztukę z przedziału $⟨3;3,50⟩\mathrm{z}ł$.

jeżeli dysponujemy zbiorem danych: $x_1$, $x_2$, $\dots$, $x_n$ o wagach odpowiednio: $w_1$, $w_2$, $\dots$, $w_n$, to średnią harmoniczną ważoną oblicza się według wzoru:$s_{hw}=\frac{w_1+w_2+\cdots +w_n}{\frac{w_1}{x_1}+\frac{w_2}{x_2}+\cdots +\frac{w_n}{x_n}}$

to zdanie złożone z dwóch zdań połączonych spójnikiem logicznym i; spójnik logiczny i w matematyce oznacza się symbolem $\wedge$; koniunkcję zdań $p$ i $q$ zapisujemy tak: $p\wedge q$; koniunkcja jest prawdziwa wtedy i tylko wtedy, gdy każde ze zdań $p$ oraz $q$ jest prawdziwe.