Przeczytaj

Przed przystąpieniem do wykonywania zadań, przypomnijmy definicję jednomianu i algorytm rozwiązywania nierówności wymiernych.

Jednomianu

Definicja: Jednomianu

Jednomianem nazywamy wyrażenie algebraiczne, które jest liczbą, literą lub iloczynem liczb i liter,

np. $(- 5)$ ; $2 x$ ; $4 x^{5}$ ; $0, 56 x^{8}$ .

Algorytm rozwiązywania nierówności wymiernych

$I$ sposób:

Wyznaczamy dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej.
Sprowadzamy nierówność do postaci ogólnej - przenosimy wszystkie wyrażenia na jedną stronę nierówności.
Wykonujemy wskazane działania.
Nierówność wymierną rozwiązujemy doprowadzając ją do równoważnej postaci wielomianowej przy wyznaczonej dziedzinie nierówności wymiernejdziedzina nierówności wymiernejdziedzinie nierówności wymiernej (zastępujemy iloraz iloczynem z uwzględnieniem założeń).
Wyznaczamy pierwiastki wielomianupierwiastek wielomianupierwiastki wielomianu oraz szkicujemy wykres.
Z wykresu odczytujemy zbiór rozwiązań danej nierówności.
Wyznaczamy rozwiązanie nierówności wymiernej uwzględniając dziedzinę.

$II$ sposób:

Wyznaczamy dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej.
Mnożymy obustronnie nierówność przez kwadrat mianownika lub przez inne wyrażenia, których znak jest jednoznacznie określony.
Wykonujemy wskazane działania.
Wyznaczamy pierwiastki wielomianu oraz szkicujemy wykres.
Z wykresu odczytujemy zbiór rozwiązań danej nierówności.
Wyznaczamy rozwiązanie nierówności wymiernej uwzględniając dziedzinę.

Zwróćmy uwagę na to , że przy rozwiązywaniu nierówności wymiernej II sposobem, nie możemy mnożyć obustronnie nierówności przez mianownik wyrażenia wymiernego, jeśli nie wiemy jaki on ma znak, czy ujemny, czy dodatni. Jeśli znak mianownika byłby ujemny, to po pomnożeniu nierówności przez ten mianownik, musielibyśmy zmienić zwrot nierówności.

Ważne!

Rozwiązując nierówność wymierną pamiętajmy o wyznaczeniu dziedziny.

Przykład 1

Rozwiążemy nierówność $\frac{(x - 2) (x + 2)}{x^{3}} \geq 0$ .

Rozwiązanie:

$D = ℝ ∖ \{0\}$ .

Zapisujemy nierówność $\frac{(x - 2) (x + 2)}{x^{3}} \geq 0$ w postaci równoważnej nierówności iloczynowej

$(x - 2) (x + 2) x^{3} \geq 0 \land x \neq 0$ .

Wielomian $W (x) = x^{3} (x - 2) (x + 2)$ jest wielomianem piątego stopnia ( $a_{5} = 1$ ). Wielomian ten ma jeden pierwiastek trzykrotny: $0$ oraz dwa pierwiastki jednokrotne: $(- 2)$ ; $2$ .

Uwzględniając dziedzinę nierówności $D = ℝ ∖ \{0\}$ rysujemy szkic wykresu.

RulhqhzYdFnp1

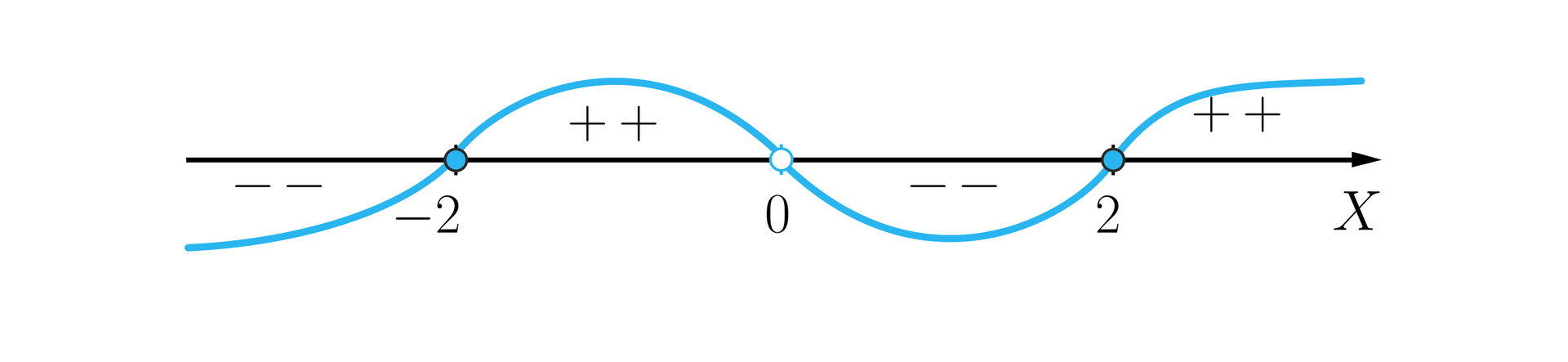
Na ilustracji przedstawiono wykres funkcji z poziomą osią X. Wykres przecina oś X w zamalowanym punkcie minus dwa, niezamalowanym punkcie zero, oraz zamalowanym punkcie dwa. Od minus nieskończoności do minus dwóch, oraz od zera do dwóch, funkcja przyjmuje wartości ujemne i wykres znajduje się pod osią X. Od minus dwóch do zera, oraz od dwóch do plus nieskończoności, funkcja przyjmuje wartości dodatnie, a jej wykres znajduje się nad osią X.

Odpowiedź: Rozwiązaniem nierówności jest zbiór $⟨- 2; 0) \cup ⟨2; + \infty)$ .

Przykład 2

Wyznaczmy sumę całkowitych rozwiązań nierównośći $\frac{- x^{2} (- x^{2} + 8 x - 16) (x^{2} - 16)}{x^{6}} \leq 0$ .

Rozwiązanie:

$D = ℝ ∖ \{0\}$ .

Pomnóżmy obustronnie nierówność przez $x^{6}$ , bo dla $x \in ℝ ∖ \{0\}$ , $x^{6} > 0$ .

Stąd

$- x^{2} (- x^{2} + 8 x - 16) (x^{2} - 16) \leq 0$ ,

$x^{2} (x^{2} - 8 x + 16) (x^{2} - 16) \leq 0$ .

Skorzystamy ze wzorów skróconego mnożenia:

$x^{2} {(x - 4)}^{2} (x - 4) (x + 4) \leq 0$ ,

$x^{2} {(x - 4)}^{3} (x + 4) \leq 0$ .

Wielomian $P (x) = x^{2} {(x - 4)}^{3} (x + 4)$ ma jeden pierwiastek trzykrotny: $4$ , jeden pierwiastek dwukrotny: $0$ oraz jeden pierwiastek jednokrotny: $(- 4)$ .

Uwzględniając dziedzinę nierówności $D = ℝ ∖ \{0\}$ , sporządzamy szkic wykresu.

RzrgHnlW841Vm

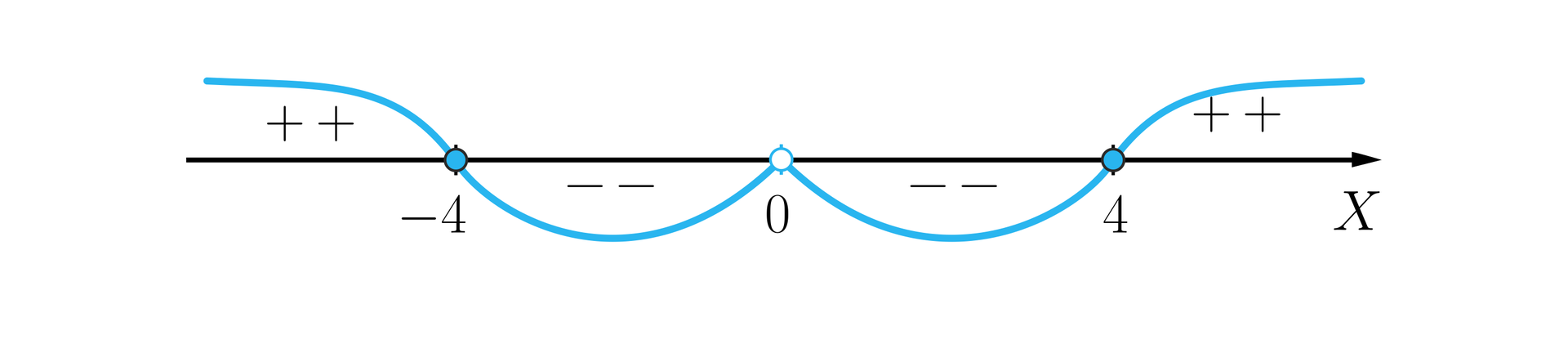
Na ilustracji przedstawiono wykres funkcji z poziomą osią X. Wykres przecina oś X w zamalowanym punkcie minus cztery, oraz w zamalowanym punkcie cztery. W niezamalowanym punkcie zero, wykres odbija się od osi X. Od minus nieskończoności do minus czterech, oraz od czterech do plus nieskończoności funkcja przyjmuje wartości dodatnie, więc wykres znajduje się nad osią X. Od minus czterech do czterech funkcja przyjmuje wartości ujemne, a jej wykres znajduje się pod osią X.

Rozwiązaniem nierówności $\frac{- x^{2} (- x^{2} + 8 x - 16) (x^{2} - 16)}{x^{6}} \leq 0$ jest zbiór $⟨- 4; 0) \cup (0; 4⟩$ .

Zauważmy, że liczby całkowite spełniające nierówność to:

$(- 4); (- 3); (- 2); (- 1); 1; 2; 3; 4$ .

Odpowiedź: Suma całkowitych rozwiązań nierówności $\frac{- x^{2} (- x^{2} + 8 x - 16) (x^{2} - 16)}{x^{6}} \leq 0$ wynosi $0$ .

Już wiesz

Nierówność wielomianową $\frac{- x^{2} (- x^{2} + 8 x - 16) (x^{2} - 16)}{x^{6}} \leq 0$ , gdzie $D = ℝ ∖ \{0\}$ możesz rozwiązać za pomocą tabeli zwanej „siatką znaków”.

Przypomnijmy, że w pierwszej kolumnie wypisujemy kolejne czynniki występujące w rozkładzie wielomianu, czyli $x + 4$ , $x^{2}$ , ${(x - 4)}^{3}$ .

Między przedziałami umieszczamy miejsca zerowe wielomianu: $(- 4)$ , $0$ , $4$ .

W kolumnach pod przedziałami zapisujemy znaki przyjmowane w tych przedziałach przez czynniki wskazane w pierwszej kolumnie.

Ostatni wiersz jest najważniejszy, bo informuje nas o znakach wielomianu $P (x)$ w poszczególnych przedziałach.

Wielomian	$(- \infty; - 4)$	$- 4$	$(- 4; 0)$	$0$	$(0; 4)$	$4$	$(4; + \infty)$
$x + 4$	$-$	$0$	$+$	$+$	$+$	$+$	$+$
$x^{2}$	$+$	$+$	$+$	$0$	$+$	$+$	$+$
${(x - 4)}^{3}$	$-$	$-$	$-$	$-$	$-$	$0$	$+$
$P (x) = x^{2} {(x - 4)}^{3} (x + 4)$	$+$	$0$	$-$	$X$	$-$	$0$	$-$

Ze względu na dziedzinę nierówności wymiernej w kolumnie oznaczonej $0$ w ostatnim wierszu wpisujemy $X$ , ponieważ $0 \notin D$ .

Z „siatki znaków” odczytujemy, że

$x^{2} {(x - 4)}^{3} (x + 4) \leq 0 \Leftrightarrow x \in ⟨- 4; 0) \cup (0; 4⟩$ .

Przykład 3

Rozwiążemy nierówność $\frac{(x + 4) (x^{2} + 9)}{x^{2}} > - x^{2} - 9$ .

Rozwiązanie:

$D = ℝ ∖ \{0\}$ .

Pomnóżmy obie strony nierówności $\frac{(x + 4) (x^{2} + 9)}{x^{2}} > - x^{2} - 9$ przez $x^{2}$ .

Dla $x \in D = ℝ ∖ \{0\}$ , $x^{2} > 0$ .

Stąd:

$\frac{(x + 4) (x^{2} + 9)}{x^{2}} > - x^{2} - 9 / \cdot x^{2}$ ,

$(x + 4) (x^{2} + 9) > x^{2} (- x^{2} - 9)$ ,

$(x + 4) (x^{2} + 9) - x^{2} (- x^{2} - 9) > 0$ ,

$(x + 4) (x^{2} + 9) + x^{2} (x^{2} + 9) > 0$ .

Zapiszmy nierówność w postaci iloczynowej

$(x^{2} + x + 4) (x^{2} + 9) > 0$ .

Wielomian $R (x) = (x^{2} + x + 4) (x^{2} + 9)$ nie ma pierwiastków rzeczywistych.

Uwzględniając dziedzinę nierówności $D = ℝ ∖ \{0\}$ rysujemy szkic wykresu.

R1W5jI8YtJjTK

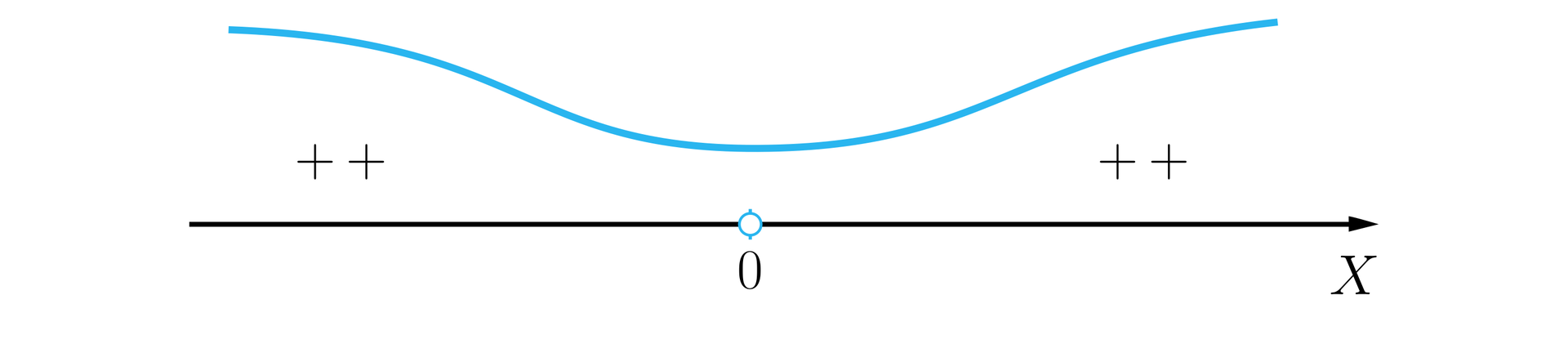
Na ilustracji przedstawiono wykres funkcji z poziomą osią X. Na osi zaznaczono niezamalowany punkt zero. Wykres funkcji jest krzywą, która nad punktem zero zbliża się do osi. W całości znajduje się nad osią X.

Odpowiedź: Rozwiązaniem nierówności jest $ℝ ∖ \{0\}$ . Zatem nierówność jest nierównością tożsamościowąnierówność tożsamościowanierównością tożsamościową.

Przykład 4

Rozwiążemy nierówność $\frac{(- x^{2} - 6 x - 1) {(8 x^{3} + 27)}^{2}}{{(x - 1)}^{2}} > {(- 8 x^{3} - 27)}^{2}$ .

Rozwiązanie:

$D = ℝ ∖ \{1\}$ .

Pomnóżmy obie strony nierówności $\frac{(- x^{2} - 6 x - 1) {(8 x^{3} + 27)}^{2}}{{(x - 1)}^{2}} > {(- 8 x^{3} - 27)}^{2}$ przez ${(x - 1)}^{2}$ .

Dla $x \in D = ℝ ∖ \{1\}$ , $(x - 1)^{2} > 0$ .

Stąd:

$\frac{(- x^{2} - 6 x - 1) {(8 x^{3} + 27)}^{2}}{{(x - 1)}^{2}} > {(- 8 x^{3} - 27)}^{2} / \cdot {(x - 1)}^{2}$ ,

$(- x^{2} - 6 x - 1) {(8 x^{3} + 27)}^{2} > {(- 8 x^{3} - 27)}^{2} {(x - 1)}^{2}$ ,

$(- x^{2} - 6 x - 1) {(8 x^{3} + 27)}^{2} - {(8 x^{3} + 27)}^{2} {(x - 1)}^{2} > 0$ ,

$(- x^{2} - 6 x - 1) {(8 x^{3} + 27)}^{2} - {(8 x^{3} + 27)}^{2} (x^{2} - 2 x + 1) > 0$ .

Zapiszmy nierówność w postaci iloczynowej

${(8 x^{3} + 27)}^{2} (- 2 x^{2} - 4 x - 2) > 0$ .

Wielomian $S (x) = {(8 x^{3} + 27)}^{2} (- 2 x^{2} - 4 x - 2)$ ma dwa pierwiastki dwukrotne: $- 1 \frac{1}{2}$ , $- 1$ .

Uwzględniając dziedzinę nierówności $D = ℝ ∖ \{1\}$ rysujemy szkic wykresu.

RIhIdjbSeUqdk

Na ilustracji przedstawiono wykres funkcji z poziomą osią X. Na osi zaznaczono zamalowany punkt minus jeden i pół, zamalowany punkt minus jeden, oraz niezamalowany punkt jeden. W punkcie minus jeden i pół, oraz minus jeden, wykres odbija się od osi X. Funkcja jest ujemna w przedziałach od minus nieskończoności do minus jeden i pół, od minus jeden i pół do -1, oraz od -1 do plus nieskończoności. Wykres funkcji w całości znajduje się pod osią X.

Odpowiedź: Rozwiązaniem nierówności jest zbiór pusty. Zatem nierówność jest nierównością sprzecznąnierówność sprzecznanierównością sprzeczną.

Słownik

dziedzina nierówności wymiernej

dziedziną nierówności wymiernej są wszystkie liczby rzeczywiste za wyjątkiem pierwiastków wielomianu $W_{2} (x)$ znajdującego się w mianowniku danego wyrażenia $\frac{W_{1} (x)}{W_{2} (x)}$

$D = ℝ ∖ \{x : W_{2} (x) = 0\}$

nierówność tożsamościowa

nierównością tożsamościową nazywamy nierówność, która jest spełniona przez każdą liczbę należącą do dziedziny tej nierówności.

nierówność sprzeczna

nierównością sprzeczną nazywamy nierówność, której nie spełniona żadna liczba należącą do dziedziny tej nierówności.

pierwiastek wielomianu

pierwiastkiem wielomianu $W (x)$ nazywamy liczbę rzeczywistą $a$ , dla której $W (a) = 0$

Wprowadzenie

Infografika

Algorytm rozwiązywania nierówności wymiernych

$I$ sposób:

$II$ sposób:

Słownik

Wprowadzenie

Infografika

Przeczytaj

Algorytm rozwiązywania nierówności wymiernych

I sposób:

II sposób:

Słownik

$I$ sposób:

$II$ sposób: