Przeczytaj

Funkcję określoną wzorem

f (x) = a x^{2} + b x + c, x \in ℝ

gdzie:
$a$ , $b$ , $c$ – są liczbami rzeczywistymi, przy czym $a \neq 0$ , nazywamy funkcją kwadratową.

Wykresem funkcji kwadratowej $f (x) = a x^{2} + b x + c$ dla $x \in ℝ$ , gdzie $a \neq 0$ , jest krzywa, zwana parabolą. Punkt $(p, q)$ nazywamy wierzchołkiem paraboli. Dzieli on parabolę na dwie części, które nazywamy ramionami.

p = - \frac{b}{2 a}

q = - \frac{∆}{4 a}

gdzie $∆ = b^{2} - 4 a c$ – wyróżnik trójmianu kwadratowego.

Gdy wyróżnik trójmianu kwadratowego $∆ = b^{2} - 4 a c$ jest nieujemny to funkcja ma miejsca zerowe:

x_{1} = \frac{- b + \sqrt{∆}}{2 a}

x_{2} = \frac{- b - \sqrt{∆}}{2 a}

Przeanalizujemy na początku ruch ciała wyrzuconego pod kątem $α$ do poziomu z prędkością $v_{0}$ . Torem ruchu ciała wyrzuconego pod kątem $α$ z prędkością $v_{0}$ jest wykres pewnej funkcji, będący częścią paraboli:

R1ckqZRNQUlaa

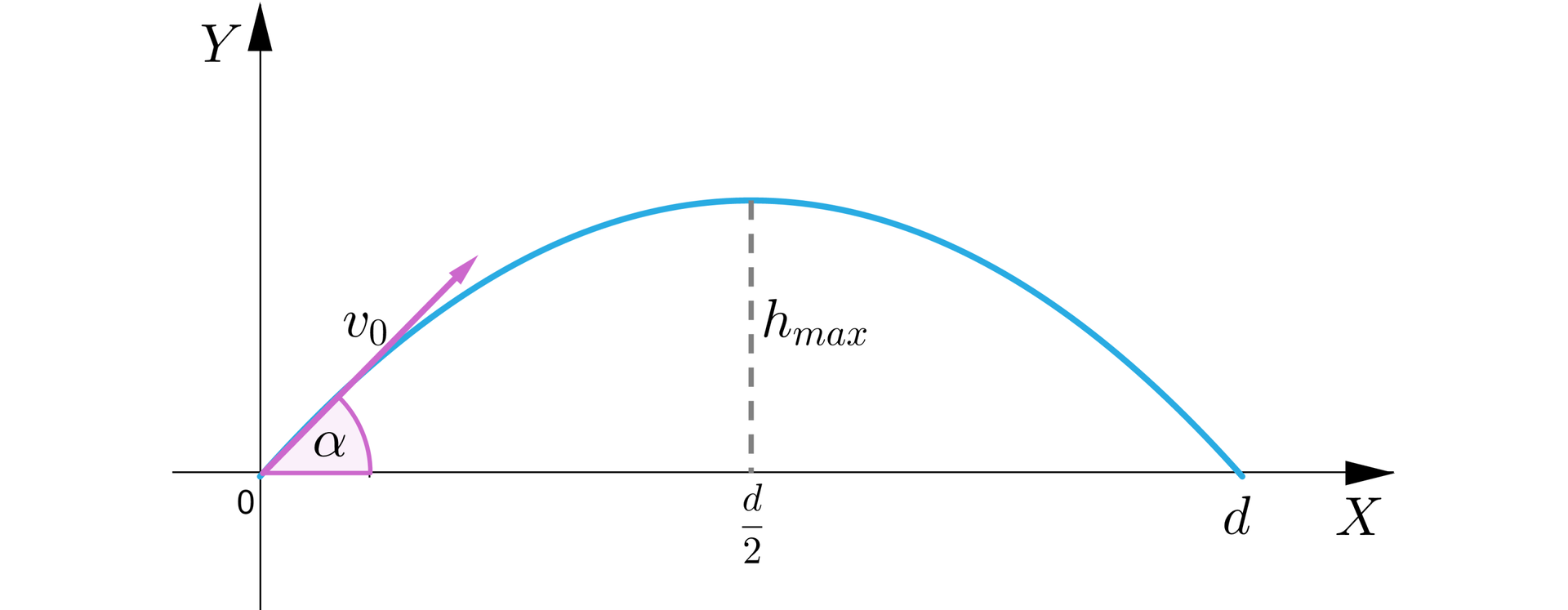
Ilustracja przedstawia poziomą oś X oraz pionową oś Y. Na rysunku zaznaczono także wykres funkcji kwadratowej będącą parabolą z wierzchołkiem w punkcie nawias d drugich średnik h indeks dolny max koniec indeksu koniec nawiasu, jest to pierwsza ćwiartka układu współrzędnych. Parabola ma ramiona skierowane w dół oraz posiada dwa miejsca zerowe, pierwsze w punkcie nawias zero średnik zero koniec nawiasu oraz drugie w punkcie nawias d średnik zero koniec nawiasu. Z punktu nawias zero średnik zero koniec nawiasu poprowadzono wektor v indeks dolny zero koniec indeksu pod kątem alfa do poziomej osi X.

Oznaczmy:

$d$ – zasięg rzutu,

$h_{m a x}$ – maksymalna wysokość, na jaką wzniesie się ciało.

Tor ruchu pocisku opisuje równanie:

y = - (\frac{g}{2 {v_{0}}^{2} \cos^{2} α}) \cdot x^{2} + (tg α) \cdot x

gdzie:

$g$ – przyśpieszenie grawitacyjne: $g = 9, 81 \frac{m}{s^{2}}$ .

Z odpowiedniego wykresu funkcji kwadratowejwykres funkcji kwadratowejwykresu funkcji kwadratowej wynika:

funkcja ma dwa miejsca zerowe: $x = 0$ i $x = d$ ,

$y = 0$ dla $x = 0$ : odpowiada momentowi wyrzutu ciała,

$y = 0$ dla $x = d$ : ciało zakończyło ruch (osiągnęło poziom, z którego zostało ciało wyrzucone),

gdy $x = \frac{d}{2}$ ciało osiąga maksymalną wysokość.

Pokażemy teraz przykładowe zadania tekstowe, w których interpretując zagadnienia przyrodnicze doprowadzimy do zapisania wzoru funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej (ograniczamy się zwykle do rozpatrywania własności takiej funkcji w pewnym przedziale). Pokażemy, jak można wykorzystać równanie toru ruchu ciała do rozwiązania zadań.

Przykład 1

Napiszemy równanie ruchu ciała wyrzuconego pod kątem $45 °$ z prędkością $20 \frac{m}{s}$ . Podamy zasięg i maksymalną wysokość, na jaką wzniesie się ciało. Przyjmiemy $g \approx 10 \frac{m}{s^{2}}$ .

Rozwiązanie

Do równania toru ruchu:

$y = - (\frac{g}{2 v_{0} {}^{2}\cos^{2} α}) \cdot x^{2} + (tg α) \cdot x$ , gdzie $x > 0$

podstawiamy dane: $v_{0} = 20 \frac{m}{s}$ , $α = 45 °$ , $g = 10 \frac{m}{s^{2}}$ .

Stąd:

$y = - (\frac{10}{2 \cdot 20^{2} \cos^{2} 45 °}) \cdot x^{2} + (tg 45 °) \cdot x$ .

Ponieważ $\cos 45 ° = \frac{\sqrt{2}}{2}$ , $tg 45 ° = 1$ ,

to:

$y = - \frac{1}{40} x^{2} + x$ .

Obliczymy teraz zasięg rzutu pamiętając, że $y = 0$ dla $x = d$ :

$0 = - \frac{1}{40} \cdot d^{2} + d = - d (\frac{1}{40} \cdot d - 1)$ .

Iloczyn jest równy zero gdy jeden z czynników jest równy zero, zatem:

$d = 0$ lub $\frac{1}{40} \cdot d - 1 = 0$ .

Stąd: $d = 40 m$ .

Zasięg tego rzutu wynosi $40 m$ .

Maksymalną wysokość obliczymy podstawiając za $x = \frac{d}{2}$ , czyli $x = 20$ .

$h_{\max} = - \frac{1}{40} \cdot 20^{2} + 20 = - \frac{1}{40} \cdot 400 + 20 = - 10 + 20$

$h_{m a x} = 10 m$

Odpowiedź

Maksymalna wysokość, na jaką wzniesie się ciało to $10 m$ , zaś zasięg rzutu wynosi $40 m$ .

Przykład 2

Obliczymy, po ilu sekundach ciało rzucone pionowo w górę z prędkością $60 \frac{m}{s}$ osiągnie wysokość $100 m$ (przyjmiemy $g \approx 10 \frac{m}{s^{2}}$ ). Wyznaczymy maksymalną wysokość, jaką osiągnie to ciało.

Rozwiązanie

Ciało wyrzucone pionowo w górę porusza się ruchem jednostajnie opóźnionym, stąd droga wyraża się wzorem:

$S = v_{0} \cdot t - \frac{a t^{2}}{2}$ ,

gdzie: $a = g = 10 \frac{m}{s^{2}}$ , $v_{0} = 60 \frac{m}{s}$ , $S = h = 100 m$ i $t > 0$ .

Po podstawieniu danych otrzymujemy:

$S = v_{0} \cdot t - \frac{a t^{2}}{2}$

$h = v_{0} \cdot t - \frac{g t^{2}}{2}$

$100 = 60 \cdot t - \frac{10 t^{2}}{2}$

$- 5 t^{2} + 60 \cdot t - 100 = 0$ .

Po podzieleniu stronami przez $(- 5)$ , otrzymujemy: $t^{2} - 12 t + 20 = 0$ , $t > 0$ .

$∆ = b^{2} - 4 a c = 12^{2} - 4 \cdot 1 \cdot 20 = 144 - 80 = 64$

Obliczamy wyznacznik trójmianu kwadratowego:

$\sqrt{∆} = \sqrt{64} = 8$ .

Obliczamy pierwiastki równania:

$t_{1} = \frac{- b + \sqrt{∆}}{2 a} = \frac{- (- 12) + \sqrt{64}}{2 \cdot 1} = \frac{12 + 8}{2} = \frac{20}{2} = 10 > 0$ ,

$t_{2} = \frac{- b - \sqrt{∆}}{2 a} = \frac{- (- 12) - \sqrt{64}}{2 \cdot 1} = \frac{12 - 8}{2} = \frac{4}{2} = 2 > 0$ .

Wyznaczymy teraz maksymalną wysokość, jaką osiągnie to ciało. Funkcja opisująca ten ruch ma postać: $f (t) = - 5 t^{2} + 60 t$ , $t > 0$ .

Maksymalną wysokość ciało osiąga w $p = \frac{- 60}{2 \cdot (- 5)} = 6$ sekundzie ruchu, zatem:

$h_{m a x} = - 5 \cdot 6^{2} + 60 \cdot 6$

$h_{m a x} = 180 m$ .

Odpowiedź

Ciało wyrzucone pionowo w górę osiągnie wysokość $100 m$ dwukrotnie: po $2$ sekundach, gdy porusza się w górę oraz po $10$ sekundach, gdy po osiągnięciu maksymalnej wysokości równej $180 m$ porusza się w dół.

Przykład 3

Odległość między dwiema przystaniami na rzece wynosi $100 km$ . Statek przepływa tę drogę w obie strony w czasie $4, 5$ godziny. Wyznaczymy prędkość statku w wodzie stojącej, jeżeli woda w rzece płynie z prędkością $5 \frac{km}{h}$ .

Rozwiązanie

Oznaczymy:

$S = 100 km$ , $t = 4, 5 h$ , $v_{r} = 5 \frac{km}{h}$ .

Wykorzystamy wzór $v = \frac{S}{t}$ przekształcony do postaci:

$t = \frac{S}{v}$ .

Niech:

$t_{1}$ – czas w godzinach, w którym statek pokonał drogę $100 km$ pod prąd, czyli z prędkością względem brzegu: $v - v_{r}$ : $t_{1} = \frac{S}{v - v_{r}}$ ,

$t_{2}$ – czas, w którym statek pokonał drogę $100 km$ z prądem, czyli z prędkością względem brzegu: $v + v_{r}$ : $t_{2} = \frac{S}{v + v_{r}}$ .

Czas całego ruchu: $t = t_{1} + t_{2}$ , zatem: $t = t_{1} + t_{2} = \frac{S}{v - v_{r}} + \frac{S}{v + v_{r}}$ .

Po podstawieniu danych otrzymujemy: $4, 5 = \frac{100}{v - 5} + \frac{100}{v + 5}$ , gdzie $v > 5 \frac{km}{h}$ .

Rozwiązujemy równanie

$4, 5 = \frac{100 \cdot (v + 5)}{(v - 5) \cdot (v + 5)} + \frac{100 \cdot (v - 5)}{(v + 5) \cdot (v - 5)}$

$4, 5 = 100 \frac{v + 5 + v - 5}{v^{2} - 25} = 100 \frac{2 v}{v^{2} - 25}$

$4, 5 = 100 \frac{2 v}{v^{2} - 25}$

$4, 5 (v^{2} - 25) = 200 v$

$4, 5 v^{2} - 4, 5 \cdot 25 = 200 v$

$4, 5 v^{2} - 112, 5 - 200 v = 0$ .

Dzielimy równanie stronami przez $5$ :

$0, 9 v^{2} - 40 v - 22, 5 = 0$ , $v > 5$ .

Obliczamy wyróżnik trójmianu:

$∆ = b^{2} - 4 a c = 40^{2} - 4 \cdot 0, 9 \cdot (- 22, 5) = 1600 + 81 = 1681$ , stąd: $\sqrt{∆} = \sqrt{1681} = 41$ .

Wyznaczamy pierwiastki równania:

$v_{1} = \frac{- b + \sqrt{∆}}{2 a} = \frac{- (- 40) + \sqrt{1681}}{2 \cdot 0, 9} = \frac{40 + 41}{1, 8} = \frac{81}{1, 8} = 45 > 5$ ,

$v_{2} = \frac{- b - \sqrt{∆}}{2 a} = \frac{- (- 40) - \sqrt{1681}}{2 \cdot 0, 9} = \frac{40 - 41}{1, 8} = \frac{- 1}{1, 8} < 5$ .

Tylko pierwsze rozwiązanie spełnia warunki zadania.

Odpowiedź

Prędkość statku w stojącej wodzie wynosi $45 \frac{km}{h}$ .

Przykład 4

Roztwór o stężeniu $40 %$ stanowi $x %$ roztworu dwuskładnikowego, pozostałą część stanowi roztwór o stężeniu $x %$ . Zapiszemy zależność stężenia roztworu dwuskładnikowego od $x$ . Wyznaczymy wartość $x$ , dla której stężenie roztworu będzie maksymalne.

Rozwiązanie

Stężenie roztworu dwuskładnikowego wyraża wzór:

$S = \frac{m_{1} + m_{2}}{M_{1} + M_{2}} \cdot 100 %$ , gdzie:

$m_{1}$ – masa substancji rozpuszczonej w pierwszym roztworze,

$m_{2}$ – masa substancji rozpuszczonej w drugim roztworze,

$M_{1}$ – masa pierwszego roztworu,

$M_{2}$ – masa drugiego roztworu.

Oznaczymy przez $M$ masę dwuskładnikowego roztworu: $M = M_{1} + M_{2}$ .

Z treści zadania:

$M_{1} = \frac{x}{100} M$ (roztwór pierwszy stanowi $x %$ całości roztworu dwuskładnikowego), $x \in (0, 100)$ ,

$M_{2} = \frac{100 - x}{100} M$ (drugi roztwór stanowi $(100 % - x %)$ całości roztworu dwuskładnikowego), $x \in (0, 100)$ ,

masa substancji $40 %$ roztworu: $m_{1} = \frac{40}{100} M_{1}$ ,

masa substancji $x %$ roztworu: $m_{2} = \frac{x}{100} M_{2}$ .

Po podstawieniu do wzoru na stężenie dwuskładnikowego roztworu otrzymujemy:

$S = \frac{\frac{40}{100} M_{1} + \frac{x}{100} M_{2}}{M_{1} + M_{2}} \cdot 100$

$S = \frac{\frac{40}{100} \cdot \frac{x}{100} \cdot M + \frac{x}{100} \cdot \frac{100 - x}{100} \cdot M}{M} \cdot 100$

$S = \frac{40}{100} x + \frac{x (100 - x)}{100}$

$S = \frac{40}{100} x + \frac{100 x - x^{2}}{100}$

$S = \frac{40}{100} x + \frac{100}{100} x - \frac{1}{100} x^{2}$

$S = \frac{- 1}{100} x^{2} + \frac{140}{100} x$

$S (x) = \frac{- 1}{100} x^{2} + 1, 4 x$ , gdzie $x \in (0, 100)$ .

Wykres rozważanej funkcji jest częścią paraboli. Aby podać współrzędne wierzchołka paraboli, możemy przedstawić funkcję w postaci kanonicznej lub wykorzystać fakt, że pierwsza współrzędna wierzchołka jest średnią arytmetyczną miejsc zerowych. Zauważmy, że:

$S (x) = \frac{- 1}{100} x (x - 140)$ , stąd $x_{1} = 0$ lub $x_{2} = 140$ .

Zatem:

$x_{w} = \frac{x_{1} + x_{2}}{2} = \frac{140}{2} = 70$ , $x \in (0, 100)$ ,

$y_{w} = S (70) = \frac{- 1}{100} x (x - 140) = - \frac{1}{100} \cdot 70 (70 - 140) = 49$ .

Rn3aKx0qBX9sB

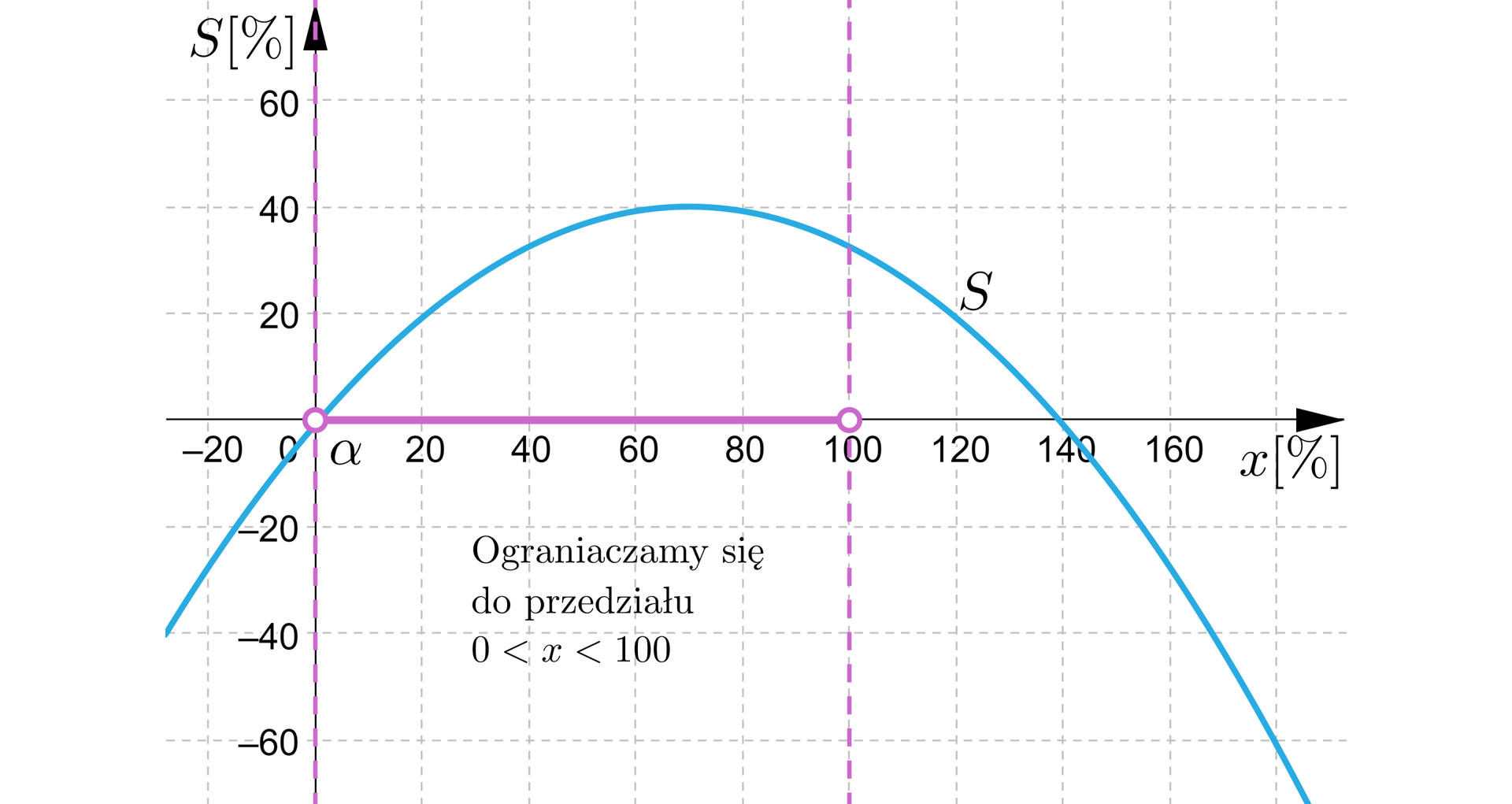
Ilustracja przedstawia poziomą oś X od minus dwudziestu do stu sześćdziesięciu oraz pionową oś S od minus sześćdziesięciu do sześćdziesięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będącej parabolą o wierzchołku w punkcie nawias siedemdziesiąt średnik czterdzieści koniec nawiasu. Parabola posiada ramiona skierowane w dół oraz dwa miejsca zerowe, pierwsze w punkcie nawias zero średnik zero koniec nawiasu oraz drugie w punkcie nawias sto czterdzieści średnik zero koniec nawiasu. Na poziomej osi X zaznaczono przedział prawo stronnie otwarty i lewostronnie otwarty od zera do stu.

Dla $x = 70 %$ otrzymujemy roztwór o maksymalnym stężeniu równym $49 %$ .

Odpowiedź

Jeżeli roztwór o stężeniu $40 %$ będzie stanowił $70 %$ roztworu dwuskładnikowego a pozostałą częścią $(30 %)$ będzie roztwór o stężeniu $70 %$ , to otrzymamy roztwór dwuskładnikowy o największym stężeniu równym $49 %$ .

Przykład 5

Korzystając z prawa Ohma obliczymy natężenie prądu płynącego w obwodzie, w którym zmiana oporu o $115 Ω$ powoduje zmniejszenie natężenia prądu o $1 A$ . Obwód jest podłączony do źródła o stałym napięciu $230 V$ .

Rozwiązanie

Prawo Ohma:

$R = \frac{U}{I}$ ,

gdzie:

$R$ – opór elektryczny,

$U$ – napięcie,

$I$ – natężenie prądu.

Oznaczymy dane (znak $Δ$ opisuje pewną zmianę): $∆ R = 115 Ω$ , $∆ I = 1 A$ , $U = 230 V$ .

Zauważmy, że przed zmianą oporu: $R = \frac{230}{I}$ , zaś po zwiększeniu oporu: $R + ∆ R = \frac{230}{I - ∆ I}$ , gdzie $R > 0$ i $I > 0$ .

Mamy zatem:

$R + 115 = \frac{230}{I - 1}$

$\frac{230}{I} + 115 = \frac{230}{I - 1}$ .

Podzielmy to równanie przez $115$ :

$\frac{2}{I} + 1 = \frac{2}{I - 1}$ , $I \neq 0$ i $I \neq 1$ .

Mnożąc równanie stronami przez $I (I - 1)$ otrzymujemy:

$2 (I - 1) + I (I - 1) = 2 I$

$I^{2} - I - 2 = 0$ i $I > 1$ .

Obliczamy wyróżnik trójmianu:

$∆ = b^{2} - 4 a c = 1^{2} - 4 \cdot 1 \cdot (- 2) = 1 + 8 = 9$ , stąd: $\sqrt{∆} = \sqrt{9} = 3$ .

Obliczamy pierwiastki równania:

$I_{1} = \frac{- b + \sqrt{∆}}{2 a} = \frac{- (- 1) + \sqrt{9}}{2 \cdot 1} = \frac{1 + 3}{2} = \frac{4}{2} = 2 > 1$ ,

$I_{2} = \frac{- b - \sqrt{∆}}{2 a} = \frac{- (- 1) - \sqrt{9}}{2 \cdot 1} = \frac{1 - 3}{2} = \frac{- 2}{2} = - 1 < 1$ .

Odpowiedź

W obwodzie płynął prąd o natężeniu $2 A$ .

Słownik

funkcja kwadratowa

funkcję

f (x) = a x^{2} + b x + c

określoną dla wszystkich liczb rzeczywistych, gdzie:
$a$ , $b$ , $c$ są liczbami rzeczywistymi, przy czym $a \neq 0$ , nazywamy funkcją kwadratową

wykres funkcji kwadratowej

wykresem funkcji kwadratowej $f (x) = a x^{2} + b x + c$ dla $x \in ℝ$ , gdzie $a \neq 0$ jest krzywa zwana parabolą

Wprowadzenie

Animacja

Słownik