Hodowca koni zamierza zbudować ogrodzenie ograniczające dwa jednakowe prostokątne boksy (patrz rysunek). Właściciel koni zakupił materiały pozwalające zbudować ogrodzenie o łącznej długości $60 \mathrm{m}$ i chce, aby powierzchnia boksów była możliwie największa. Wyznaczymy wymiary każdego boksu.

RmCs7KN0my178

Ilustracja przedstawia dwa identyczne prostokąty, które mają wspólny jeden bok.

Rozwiązanie:

Oznaczmy:

R1APOK2BhORrM

Ilustracja przedstawia dwa identyczne prostokąty, które mają wspólny jeden bok. W lewym prostokącie oznaczono dłuższy pionowy bok literą y, a krótszy poziomy bok literą x.

Zapiszmy równanie wynikające z długości ogrodzenia boksów $4x+3y=60$. Wyznaczymy jedną zmienną $y=20-\frac{4}{3}x$. Pole dwóch prostokątów wynosi

$P\left(x\right)=2x\left(20-\frac{4}{3}x\right)$

Długości boków muszą być liczbami dodatnimi, więc dziedziną funkcji $P$ jest zbiór $D=\left(0,15\right)$

Naszkicujemy wykres tej funkcji. Jest to funkcja kwadratowafunkcja kwadratowafunkcja kwadratowa, współczynnik przy najwyższej potędze jest ujemny, więc ramiona paraboli skierowane są w dół.

RXS6ryIS2NszI

Ilustracja przedstawia narysowaną parabolę w układzie współrzędnych kartezjańskich. Ramiona paraboli skierowane są w dół, jej wierzchołek znajduje się w pierwszej ćwiartce, poza tym parabola biegnie również w trzeciej i czwartej ćwiartce. Parabola posiada dwa miejsca zerowe zaznaczone niezamalowanymi kółkami. Pierwsze dla argumentu zero, drugie dla argumentu piętnaście.

Pierwsza współrzędna wierzchołka paraboli $x_w$, jest średnią arytmetyczną miejsc zerowych, zatem $x_w=\frac{0+15}{2}=7,5 \mathrm{cm}$. Zauważmy, że należy do dziedziny funkcji, zatem funkcja przyjmuje największą wartość w wierzchołku paraboli. Wyznaczymy $y=20-\frac{4}{3}x=20-\frac{4}{3}·7,5=10 \mathrm{cm}$.

Odpowiedź:

Wymiary każdego boksu wynoszą $7,5 \mathrm{cm}\times 10 \mathrm{cm}$.

Drewnianą listwę o długości $0,8 \mathrm{m}$ i szerokości $4 \mathrm{cm}$ należy pociąć na takie cztery części, aby po ich sklejeniu (zobacz rysunek) otrzymać ramę, w którą można oprawić obraz. Wyznaczymy maksymalne pole powierzchni obrazu, który może być oprawiony w tak zbudowaną ramę.

RojA0zATYeyRX

Zdjęcie przedstawia prostokątną drewnianą ramę stworzoną z czterech listew.

Rozwiązanie:

Oznaczmy:

RNjYFuUcUYXZn

Ilustracja przedstawia szkic geometryczny uzyskanej wcześniej drewnianej ramy. Długość dłuższej listwy została oznaczona jako y, długość krótszej jako x.

Znając długość listwy możemy zapisać równanie $2x+2y=80 \mathrm{cm}$. Wyznaczmy jedną zmienną $y=40-x$. Pole obrazu

$P=\left(x-4\right)\left(y-4\right)$

Podstawiając za $y=40-x$ otrzymujemy funkcję wyrażającą pole obrazu

$P\left(x\right)=\left(x-4\right)\left(36-x\right)$

Biorąc pod uwagę, że długości boków muszą być liczbami dodatnimi, wyznaczamy dziedzinę funkcji $P$.

$D=\left(4,36\right)$

Naszkicujemy wykres funkcji, współczynnik przy najwyższej potędze jest ujemny, więc ramiona paraboli skierowane są w dół.

R6HGqTzAzfvQh

Ilustracja przedstawia narysowaną parabolę w układzie współrzędnych kartezjańskich. Ramiona paraboli skierowane są w dół, jej wierzchołek znajduje się w pierwszej ćwiartce, poza tym parabola biegnie również w trzeciej i czwartej ćwiartce. Parabola posiada dwa miejsca zerowe zaznaczone niezamalowanymi kółkami. Pierwsze dla argumentu cztery, drugie dla argumentu trzydzieści sześć.

Pierwsza współrzędna wierzchołka paraboli $x_w$, jest średnią arytmetyczną miejsc zerowych, zatem $x_w=\frac{4+36}{2}=20 \mathrm{cm}$. Zauważmy, że należy do dziedziny funkcji, zatem funkcja przyjmuje największą wartość w wierzchołku paraboli. Wyznaczymy $y=40-x=40-20=20 \mathrm{cm}$. Maksymalne pole powierzchni obrazu wynosi

$P\left(20\right)=\left(20-4\right)\left(36-20\right)=256 {\mathrm{cm}}^2$.

Z kawałka blachy w kształcie trapezu równoramiennego o polu $3 {\mathrm{m}}^2$ i podstawach długości $80 \mathrm{cm}$ i $220 \mathrm{cm}$ należy wyciąć prostokąt o maksymalnym polu (zobacz rysunek). Wyznaczymy wymiary wyciętego prostokąta.

R5UFn4xCtwJtI

Zdjęcie przedstawia kawałek blachy w kształcie trapezu równoramiennego. Na blasze zaznaczono linią przerywaną prostokąt o jak największym możliwym polu powierzchni. W prostokącie zaznaczono kąty proste.

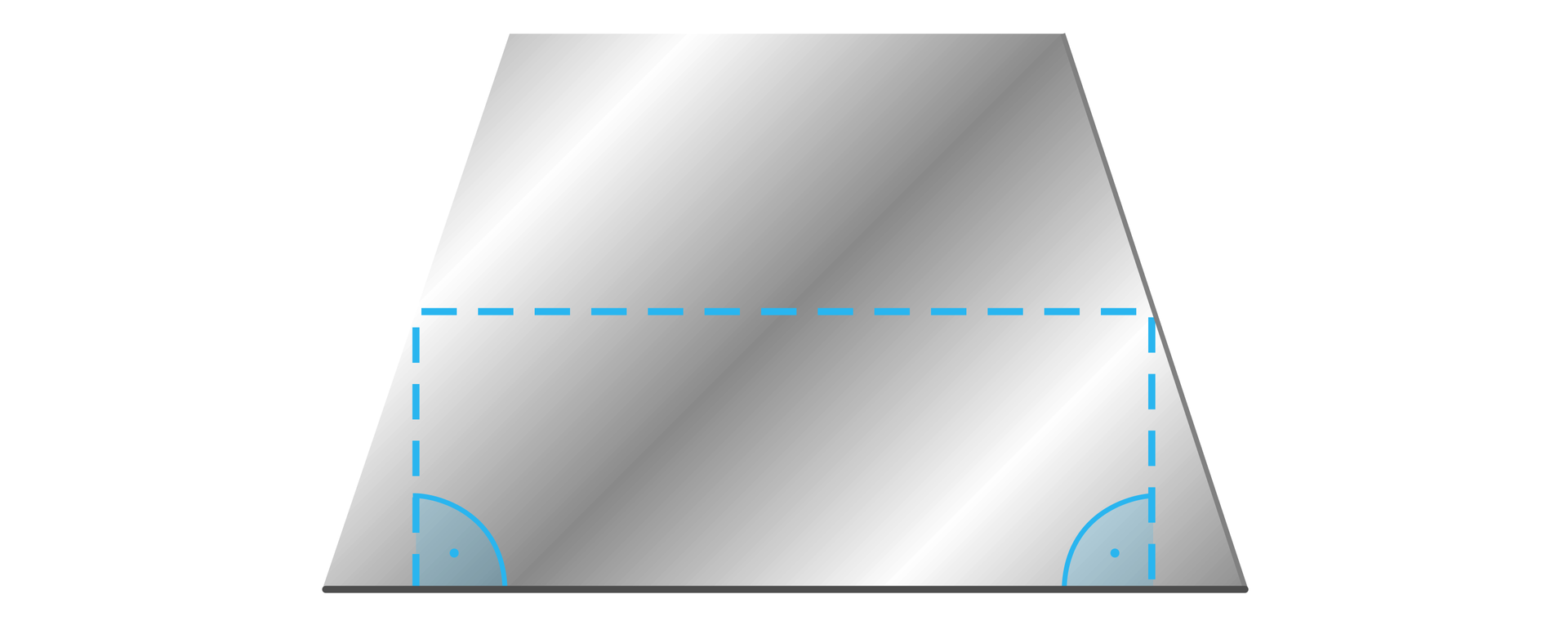
Rozwiązanie:

Oznaczmy:

RTjKC2l66ixpO

Ilustracja przedstawia trapez równoramienny i wrysowany weń prostokąt. Wierzchołki trapezu zostały oznaczone literami A, B, C i D. Dłuższy bok prostokąta oznaczono jako x. Krótszy bok prostokąta oznaczono jako y i zawiera się on od punktu E do punktu S. Punkt E leży na dolnym odcinku trapezu. Punkt S znajduje się na ramieniu trapezu.

Z polecenia wiemy, że $\left|AB\right|=2,2 \mathrm{m}$ oraz $\left|CD\right|=0,8 \mathrm{m}$. Ze wzoru na pole trapezu wyznaczymy jego wysokość.

$P=\frac{\left(a+b\right)·h}{2}$

Podstawiamy $3=\frac{3·h}{2}$, stąd $h=2 \mathrm{m}$. W związku z tym, że $\left|CD\right|=\left|FG\right|$ oraz trapez jest równoramienny to $\left|AF\right|=\left|GB\right|=0,7 \mathrm{m}$. Przyjmując, że $\left|EH\right|=x$ mamy $\left|AE\right|=\frac{2,2-x}{2}$. Trójkąt $SAE$ oraz $DAF$ są podobnetrójkąty podobnepodobne, cecha bkb. Zapisujemy

$\frac{h}{y}=\frac{\left|AF\right|}{\left|AE\right|}$

Wyznaczając $y$ otrzymujemy

$y=\frac{h·\left|AE\right|}{\left|AF\right|}=\frac{2,2-x}{0,7}$

Następnie wyznaczamy pole prostokąta jako funkcję zmiennej $x$. Skoro $P=xy$, to

$P\left(x\right)=\frac{10}{7}x(2,2-x)$

Biorąc pod uwagę, że długości boków muszą być dodatnie określamy, że dziedziną jest zbiór $D=\left(0;2,2\right)$

Pierwsza współrzędna wierzchołka paraboli, której wykres pokrywa się z wykresem funkcji $P$, jest średnią arytmetyczną miejsc zerowych, zatem $x_w=\frac{0+2,2}{2}=1,1 \mathrm{m}$. Zauważmy, że należy do dziedziny funkcji, zatem funkcja przyjmuje największą wartość w wierzchołku paraboli. Wyznaczymy $y=\frac{2,2-x}{0,7}=\frac{11}{7} \mathrm{m}$.

Odpowiedź:

Wymiary wyciętego prostokąta to $1,1 \mathrm{m}\times \frac{11}{7} \mathrm{m}$.

Obwód okna przedstawionego na rysunku wynosi $14 \mathrm{m}$. Wyznaczymy miary odcinków $x$ i $y$ (patrz rysunek), aby przez okno wpadało jak najwięcej światła.

R1JaDJtXxTGNy

Zdjęcie przedstawia okno z białą ramą. Składa się ono z dwóch części, dolnej o kształcie prostokąta o bokach x i y, i górnej, oddzielonej ramą, w kształcie trójkąta równobocznego o boku y. Podstawa trójkąta jest jednocześnie górnym bokiem prostokąta.

Rozwiązanie:

Zapiszmy równanie wynikające z obwodu okna $2x+3y=14$. Wyznaczymy jedną ze zmiennych np. $x$ otrzymujemy $x=7-\frac{3}{2}y$. Przez okno będzie wpadać jak najwięcej światło gdy jego pole powierzchni będzie maksymalne. Okno składa się z dwóch figur: z prostokąta oraz z trójkąta równobocznegotrójkąt równobocznytrójkąta równobocznego.

$P=xy+\frac{y^2\sqrt{3}}{4}$

Podstawiając za $x$ otrzymujemy

$P\left(y\right)=\left(7-\frac{3}{2}y\right)y+\frac{y^2\sqrt{3}}{4}$

Przekształcając funkcję, otrzymujemy funkcję zmiennej $y$ wyrażającej pole powierzchni okna

$P\left(y\right)=7y+\left(\frac{\sqrt{3}}{4}-\frac{3}{2}\right)y^2$

Biorąc pod uwagę, że długości boków muszą być dodatnie, określamy, że dziedziną jest zbiór $D=\left(0,\frac{14}{3}\right)$

Wyznaczymy wierzchołek paraboli ze wzoru $-\frac{b}{2a}$. Otrzymujemy

$y=-\frac{7}{2\left(\frac{\sqrt{3}}{4}-\frac{3}{2}\right)}=-\frac{7}{\frac{\sqrt{3}}{2}-3}$

Następnie usuwamy niewymierność z mianownika

$y=-\frac{7}{\frac{\sqrt{3}}{2}-3}·\frac{\frac{\sqrt{3}}{2}+3}{\frac{\sqrt{3}}{2}+3}$

Mnożymy ułamki i upraszczamy

$y=\frac{-\frac{7\sqrt{3}}{2}-21}{\frac{3}{4}-9}=\frac{\frac{7\sqrt{3}}{2}+21}{\frac{33}{4}}=\frac{14\sqrt{3}}{33}+\frac{28}{11}$

Następnie wyznaczymy $x=7-\frac{3}{2}y=\frac{35}{11}-\frac{7\sqrt{3}}{11}$.

Odpowiedź:

Miary $x=\frac{35}{11}-\frac{7\sqrt{3}}{11} \mathrm{m}$ oraz $y=\frac{14\sqrt{3}}{33}+\frac{28}{11} \mathrm{m}$.

funkcja określona wzorem:

gdzie współczynniki $a$, $b$, $c$ są ustalonymi liczbami przy czym $a\ne 0$

dwa trójkąty których odpowiednie kąty są równe, a odpowiednie boki proporcjonalne; trójkąty są podobne gdy zachodzi którykolwiek z poniższych równoważnych warunków:

1. cecha bbb (bok–bok–bok) – stosunki długości odpowiednich par boków są równe,

2. cecha bkb (bok–kąt–bok) – stosunku długości dwóch par boków są równe i miary kątów między tymi bokami są równe,

3. cecha kkk (kąt–kąt–kąt) – zachowane są miary odpowiednich kątów

trójkąt, którego wszystkie boki mają tę samą długość