Nierównością wymierną nazywamy nierówność postaci: $\frac{W\left(x\right)}{V\left(x\right)}>0$ lub $\frac{W\left(x\right)}{V\left(x\right)}<0$, lub $\frac{W\left(x\right)}{V\left(x\right)}\ge 0$, lub $\frac{W\left(x\right)}{V\left(x\right)}\le 0$, gdzie $W\left(x\right)$ i  $V\left(x\right)$ są wielomianami i  $V\left(x\right)$ nie jest wielomianem zerowym.

Pokażemy, dla jakich wartości parametru $m$ nierówność $\frac{2m}{x^2+3}<3$ jest prawdziwa dla wszystkich liczb rzeczywistych.

Rozwiązanie:

$\frac{2m}{x^2+3}<3$

Określamy dziedzinędziedzinadziedzinę nierówności: $x\in \mathrm{ℝ}$.

Ponieważ mianownik jest stale dodatni, mnożymy nierówność obustronnie przez ten mianownik otrzymując:

$2m<3\left(x^2+3\right)$

Po wykonaniu przekształceń równoważnych oraz uporządkowaniu otrzymujemy nierówność kwadratową:

$3x^2-2m+9>0$

Ponieważ współczynnik $a$ jest dodatni, więc aby ta nierówność była prawdziwa dla wszystkich liczb rzeczywistych, jej wykres musi być położony ponad osią $X$. Zatem spełniony musi być warunek:

$\mathrm{\Delta }<0$

$\mathrm{\Delta }=-4·3·\left(-2m+9\right)=24m-108$

$24m-108<0\iff 24m<108\iff m<4\frac{1}{2}$

Odpowiedź:

Dana nierówność jest prawdziwa dla wszystkich liczb rzeczywistych dla $m\in \left(-\infty ,4\frac{1}{2}\right)$.

Pokażemy, dla jakich wartości parametru $a$ nierówność $\frac{x^3+x^2-x-1}{x-a}<0$ nie ma rozwiązań całkowitych dodatnich.

Ustalmy dziedzinę nierówności: $x\in \mathrm{ℝ}\setminus \left\{a\right\}$.

Danej nierówności przyporządkujmy równoważną jej nierówność wielomianową:

$\left(x^3+x^2-x-1\right)\left(x-a\right)<0$

Wielomian stopnia trzeciego rozłóżmy na czynniki liniowe drogą grupowania wyrazów:

$\left[x^2\left(x+1\right)-\left(x+1\right)\right]\left(x-a\right)<0$

$\left(x+1\right)\left(x^2-1\right)\left(x-a\right)<0$

$\left(x+1\right)\left(x+1\right)\left(x-1\right)\left(x-a\right)<0$

${\left(x+1\right)}^2\left(x-1\right)\left(x-a\right)<0$

Miejscami zerowymi (pierwiastkami) otrzymanego wielomianu są liczby: $x=-1$, $x=1$, $x=a$.

Zauważmy ponadto, że $x=-1$ jest pierwiastkiem podwójnympierwiastek podwójny wielomianupierwiastkiem podwójnym.

Aby przedstawić ilustrację graficzną nierówności i ustalić jej rozwiązania, należy rozważyć $5$ przypadków:

1. $a<-1$, wtedy rozwiązaniem nierówności są liczby rzeczywiste $x\in \left(a,-1\right)\cup \left(-1,1\right)$, a więc nie ma w zbiorze rozwiązań liczb całkowitych dodatnich.

   R1bL0a6RaNpL8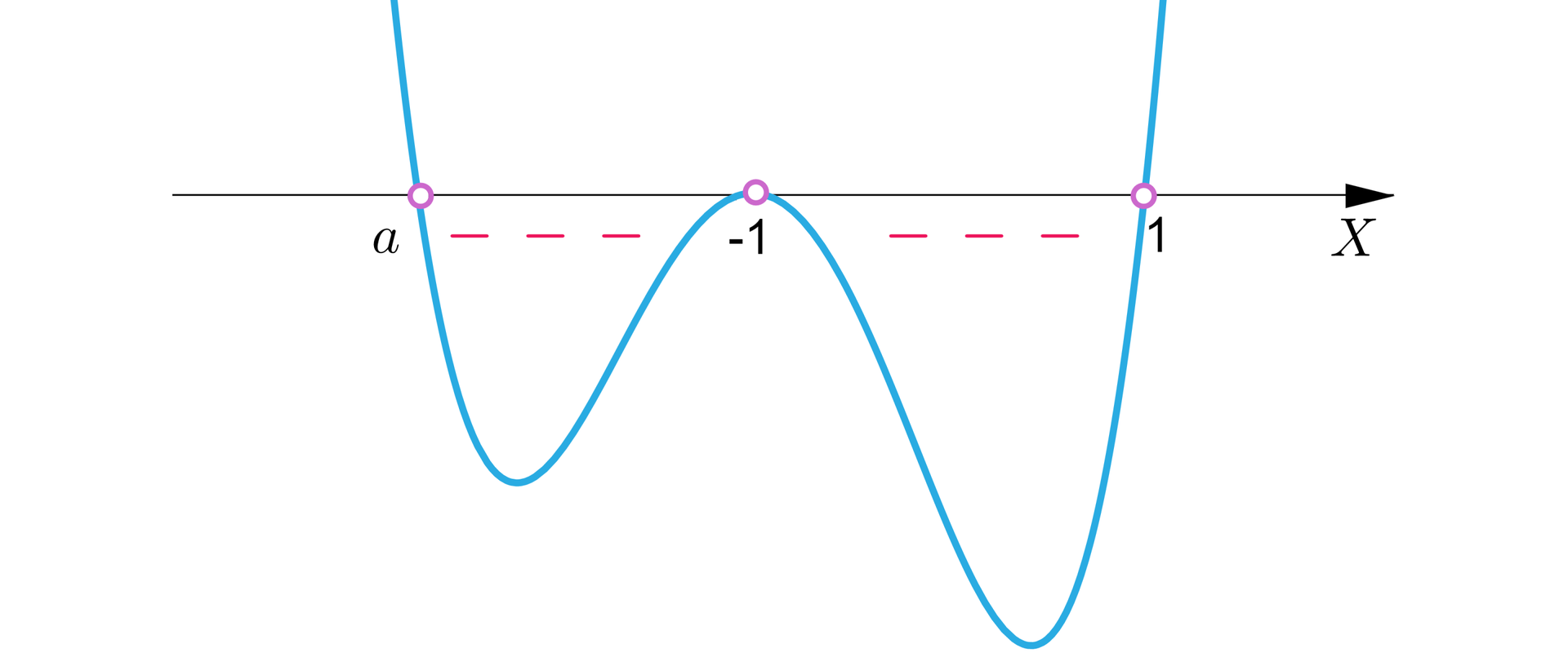

   Ilustracja przedstawia poziomą oś $X$, na której niezamalowanymi kółkami oznaczono następujące punkty od lewej: a, minus 1, jeden. Na rysunku naniesiono wykres funkcji wielomianowej biegnący w następujący sposób: od minus nieskończoności do a wykres przyjmuje wartości dodatnie i biegnie niemal pionowo w dół. W punkcie a przebija pod oś, gdzie początkowo biegnie w dół, następnie odbija w górę i biegnie do punktu minus jeden, z którego ponownie odbija w dół pod osią. Następnie w punkcie 1 wykres przebija nad oś i biegnie niemal pionowo w górę do plus nieskończoności. Minusami zaznaczono przedział, w którym funkcja przyjmuje wartości ujemne, czyli przedział otwarty od a do jeden z wyłączeniem punktu minus jeden.

   

2. $a=-1$, wtedy nierówność przyjmuje postać:

   ${\left(x+1\right)}^2\left(x-1\right)\left(x-a\right)<0$

   ${\left(x+1\right)}^2\left(x-1\right)\left(x+1\right)<0$

   ${\left(x+1\right)}^3\left(x-1\right)<0$

   Zauważmy, że $x=-1$ jest pierwiastkiem trzykrotnym wielomianupierwiastek $k$–krotny wielomianupierwiastkiem trzykrotnym wielomianu. Zatem rozwiązaniem nierówności są liczby rzeczywiste $x\in \left(-1,1\right)$, a więc nie ma w zbiorze rozwiązań liczb całkowitych dodatnich.

   RZg7kD4BbwtEk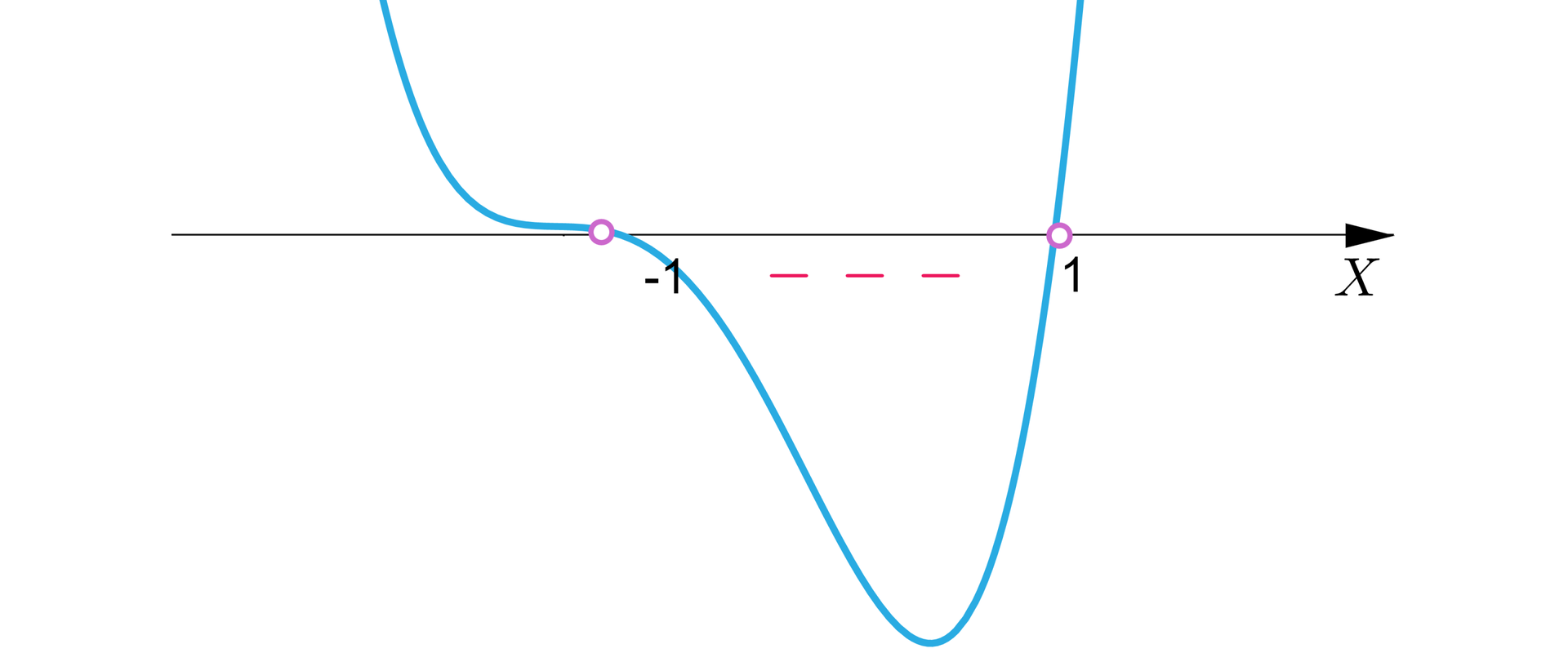

   Ilustracja przedstawia poziomą oś $X$, na której niezamalowanymi kółkami oznaczono następujące punkty minus 1 i jeden. Na rysunku naniesiono wykres funkcji wielomianowej biegnący w następujący sposób: od minus nieskończoności do -1 wykres przyjmuje wartości dodatnie i biegnie niemal pionowo w dół. W punkcie -1 przebija pod oś, gdzie początkowo biegnie w dół, następnie odbija w górę i biegnie do punktu jeden. Następnie w punkcie 1 wykres przebija nad oś i biegnie niemal pionowo w górę do plus nieskończoności. Minusami zaznaczono przedział, w którym funkcja przyjmuje wartości ujemne, czyli przedział otwarty od minus jeden do jeden.

   

3. $a\in \left(-1,1\right)$, wtedy rozwiązaniem nierówności są liczby rzeczywiste $x\in \left(a,1\right)$, a więc nie ma w zbiorze rozwiązań liczb całkowitych dodatnich.

   Ri2lewW1VBUIy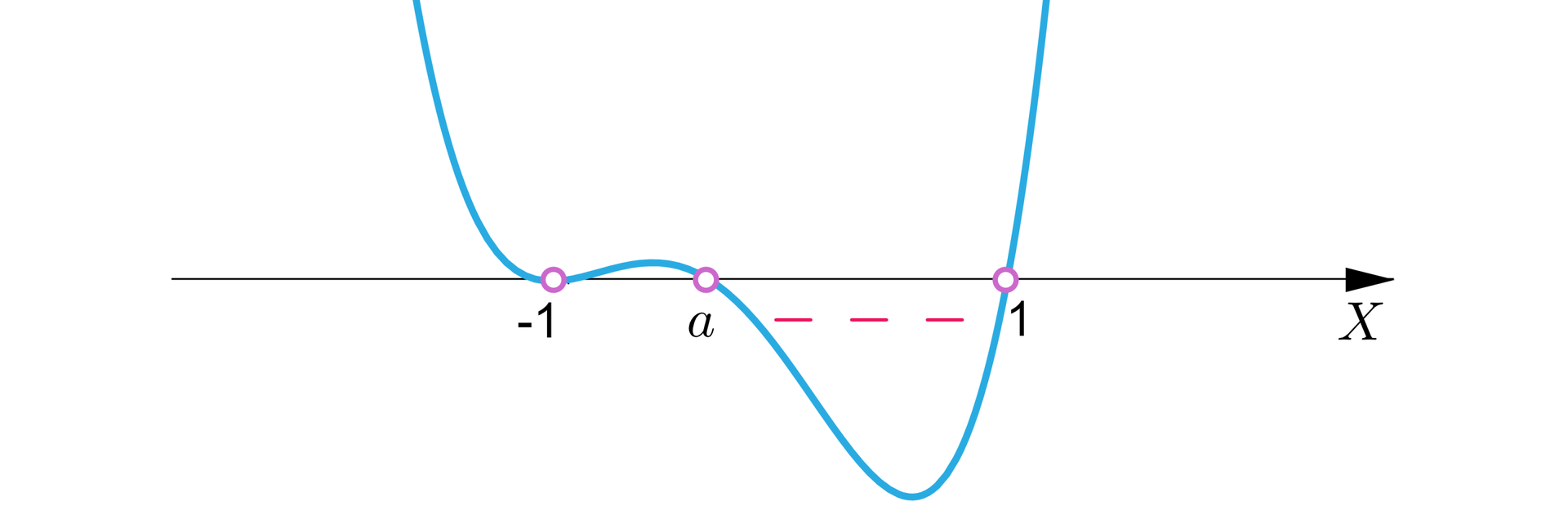

   Ilustracja przedstawia poziomą oś $X$, na której niezamalowanymi kółkami oznaczono następujące punkty od lewej: minus 1, a, jeden. Na rysunku naniesiono wykres funkcji wielomianowej biegnący w następujący sposób: od minus nieskończoności do minus 1, wykres biegnie niemal pionowo w dół, po czym odbija w górę i ponownie w dół. W punkcie a, przebija pod oś, gdzie początkowo biegnie w dół, a następnie odbija w górę i biegnie do punktu jeden. W punkcie jeden, wykres przebija nad oś i biegnie niemal pionowo w górę do plus nieskończoności. Minusami zaznaczono przedział, w którym funkcja przyjmuje wartości ujemne, czyli przedział otwarty od a do jeden.

   

4. $a=1$, wtedy nierówność przyjmuje postać:

   ${\left(x+1\right)}^2\left(x-1\right)\left(x-a\right)<0$

   $\left(x+1\right){}^2\left(x-1\right)\left(x-1\right)<0$

   ${\left(x+1\right)}^2{\left(x-1\right)}^2<0$

   Zauważmy, że oba pierwiastki $x=-1$ oraz $x=1$ są podwójne, zatem nierówność jest sprzeczna: $x\in \varnothing$, a więc nie ma w zbiorze rozwiązań liczb całkowitych dodatnich.

5. $a>1$, wtedy rozwiązaniem nierówności są liczby rzeczywiste $x\in \left(1,a\right)$, a więc o ile $a\le 2$, to nie ma w zbiorze rozwiązań liczb całkowitych dodatnich, ale jeśli $a>2$ (jak na poniższym rysunku), to zbiór rozwiązań zawiera co najmniej jedną liczbę całkowitą dodatnią.

   R1afljJtLGOWJ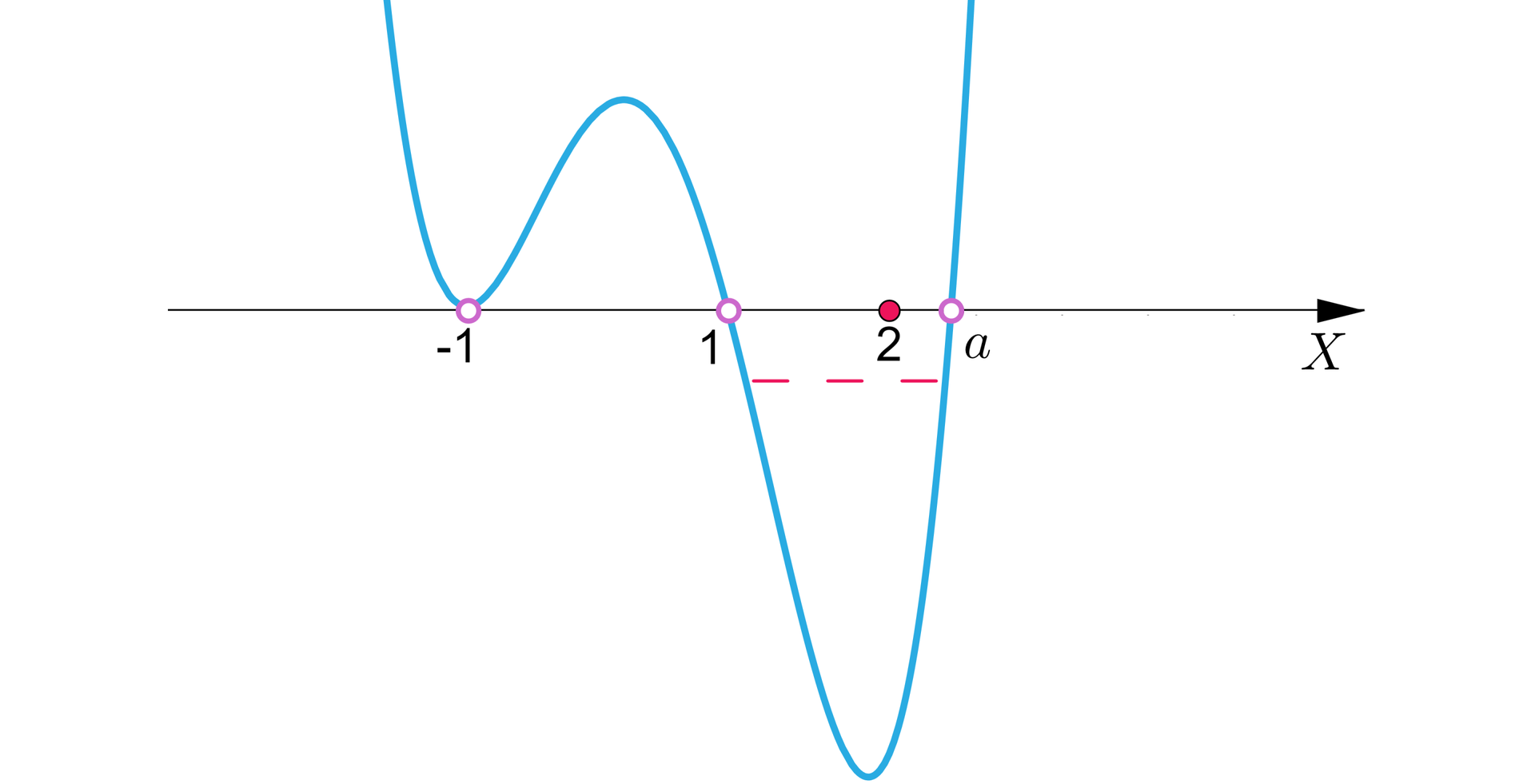

   Ilustracja przedstawia poziomą oś $X$, na której niezamalowanymi kółkami oznaczono następujące punkty od lewej: minus 1, jeden, a. Między 1 i a zaznaczono zamalowanym kółkiem punkt o współrzędnej dwa. Na rysunku naniesiono wykres funkcji wielomianowej biegnący w następujący sposób: od minus nieskończoności do minus 1, wykres biegnie niemal pionowo w dół, po czym odbija w górę i ponownie w dół. W punkcie jeden, przebija pod oś, gdzie początkowo biegnie w dół, a następnie odbija w górę i biegnie do punktu a. W punkcie a, wykres przebija nad oś i biegnie niemal pionowo w górę do plus nieskończoności. Minusami zaznaczono przedział, w którym funkcja przyjmuje wartości ujemne, czyli przedział otwarty od jeden do a.

   

Odpowiedź:

Nierówność $\frac{x^3+x^2-x-1}{x-a}<0$ nie ma rozwiązań całkowitych dodatnich dla $a\in \left(-\infty ,2\right.⟩$.

Pokażemy, dla jakich wartości parametru $b$ wykresy funkcji $f\left(x\right)=\frac{b}{x}$, gdzie $x\ne 0, b\ne 0$ oraz $g\left(x\right)=\left(b-1\right)x$ nie mają punktów wspólnych.

Zauważmy, że wykresem funkcji $f\left(x\right)=\frac{b}{x}$ jest hiperbola położona w

• $\text{I}$ i $\text{III}$ ćwiartce układu współrzędnych, jeśli $b>0$ lub

• w $\text{II}$ i $\text{IV}$ ćwiartce układu współrzędnych, jeśli $b<0$,

zaś wykresem funkcji $g\left(x\right)=\left(b-1\right)x$ jest prosta przechodząca przez początek układu współrzędnych oraz

• $\text{I}$ i $\text{III}$ ćwiartkę układu współrzędnych, jeśli $b>1$ lub

• $\text{II}$ i $\text{IV}$ ćwiartkę układu współrzędnych, jeśli $b<1$.

Aby ustalić kiedy prosta nie będzie miała punktów wspólnych z hiperbolą, rozważymy następujące przypadki uwzględniające różne położenia prostej i hiperboli:

• $b<0$ i  $b<1\iff b\in \left(-\infty ,0\right)$, np.

  RlXpXDJUUpMB1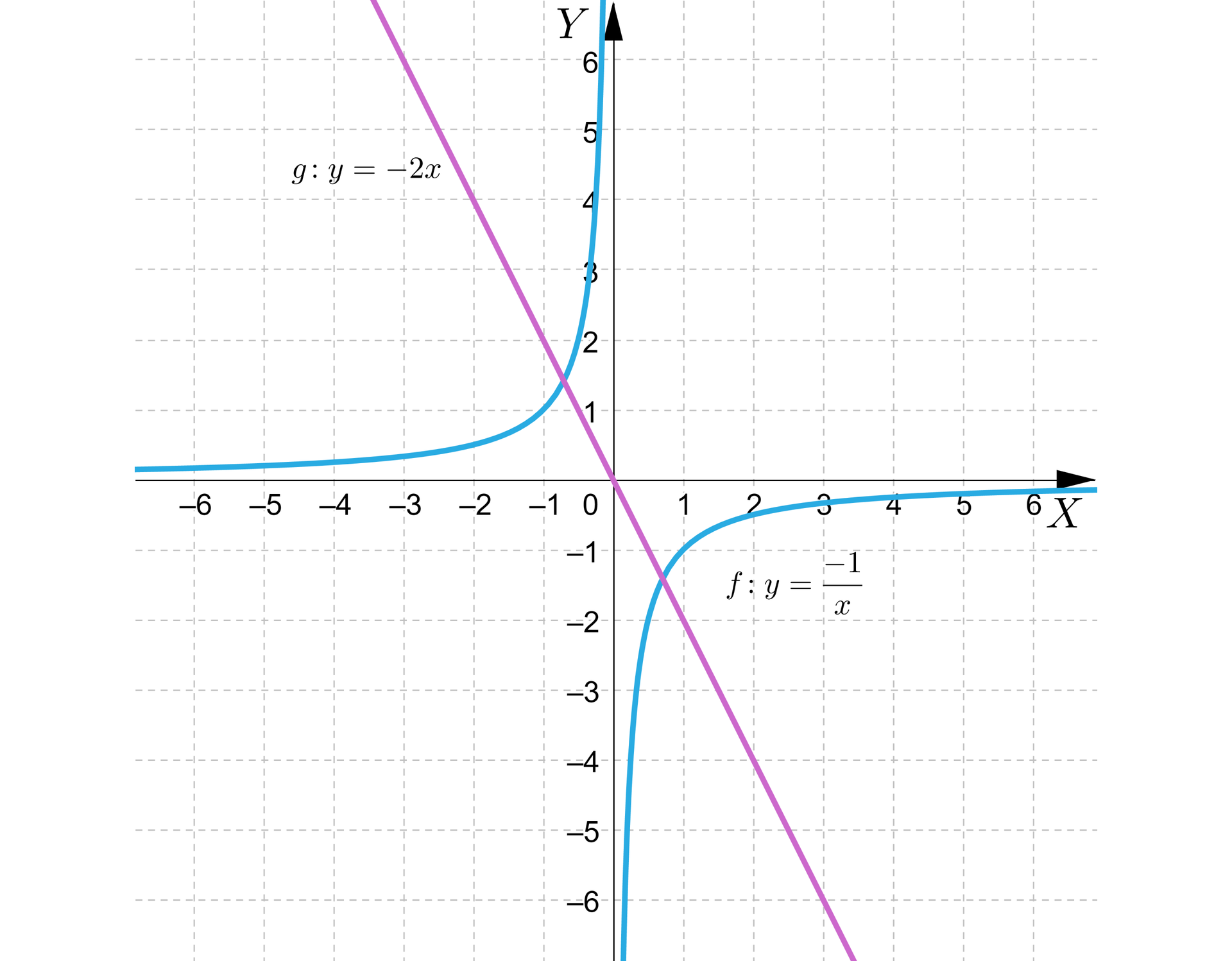

  Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus sześciu do sześciu, oraz z pionową osią $Y$ od minus sześciu do sześciu. Na płaszczyźnie narysowano wykres funkcji f od x równa się minus 1 podzielić na x, który stanowi hiperbola, której gałęzie leżą w drugiej i czwartej ćwiartce układu współrzędnych. Wykres przechodzi przez punkty $\left(-1;1\right)$, oraz $\left(1;-1\right)$. Na wykresie poprowadzono ukośną prostą będącą wykresem funkcji g od x równa się minus 2 x, przechodzącą przez początek układu współrzędnych oraz punkty $\left(-1;2\right)$, $\left(1;-2\right)$. Prosta przecina obie gałęzie hiperboli.

  

  Grafika pokazuje, że w takim przypadku wykresy funkcji mają zawsze dwa punkty wspólne, ponieważ „zajmują” te same ćwiartki układu współrzędnych.

• $b<0$ i $b>1\iff b\in \varnothing$.

• $b>0$ i $b<1\iff b\in \left(0,1\right)$, np.

  RTH9NuLvQLtX7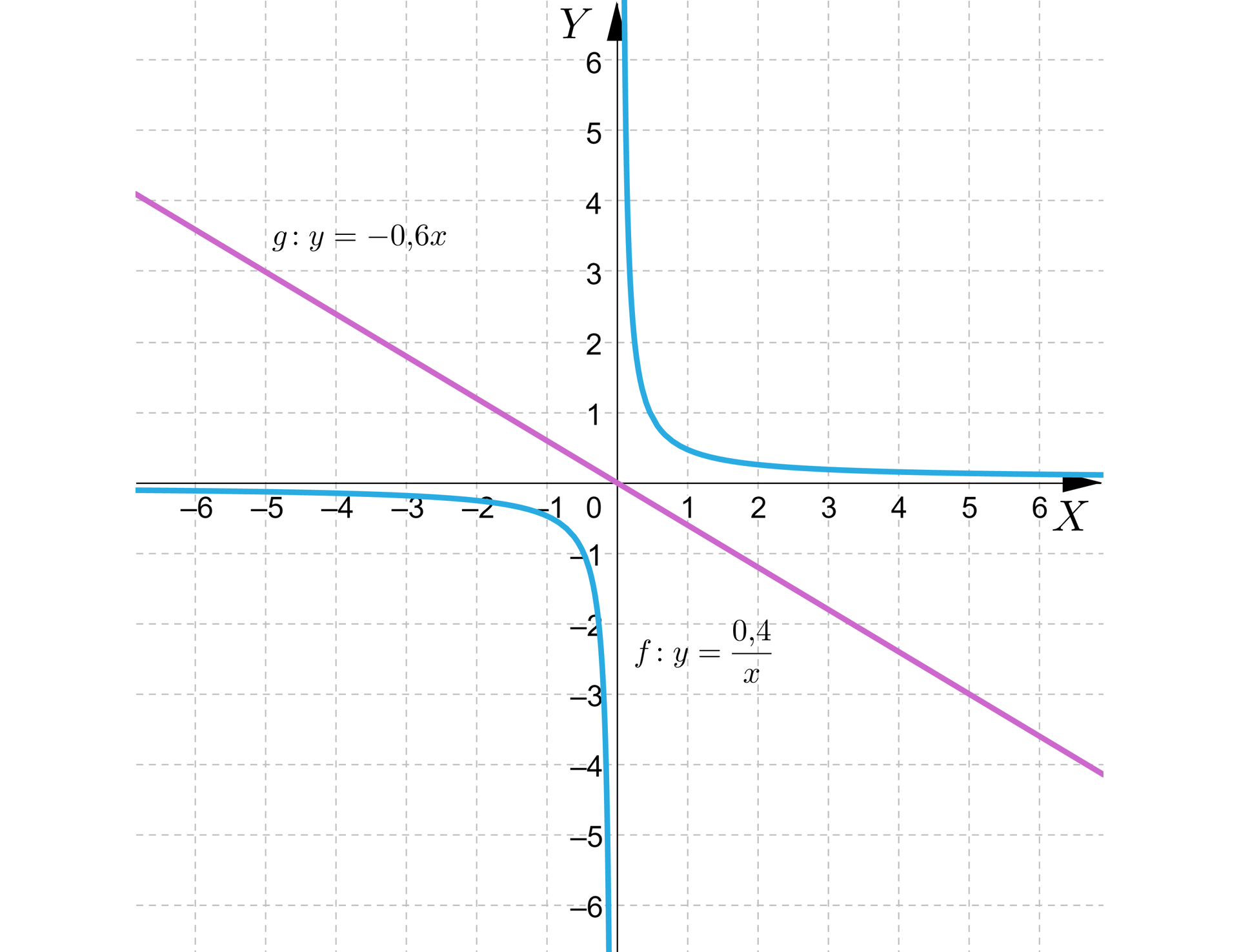

  Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus sześciu do sześciu, oraz z pionową osią $Y$ od minus sześciu do sześciu. Na płaszczyźnie narysowano wykres funkcji. Wykresem funkcji f od x równa się 0,4 podzielić na x jest hiperbola, której gałęzie leżą w pierwszej i trzeciej ćwiartce układu współrzędnych. Na wykresie poprowadzono ukośną prostą, będącą wykresem funkcji g od x równa się minus 0,6 x, przechodzącą przez początek układu współrzędnych oraz punkty $\left(-5;3\right)$, oraz $\left(5;-3\right)$. Prosta nie ma punktów wspólnych z wykresem funkcji.

  

  W tym przypadku wykresy funkcji przebiegają przez różne ćwiartki układu współrzędnych, a zatem nie mają punktów wspólnych.

• $b>0$ i $b>1\iff b\in \left(1,\infty \right)$, np.

  R1RFheG3h8mRA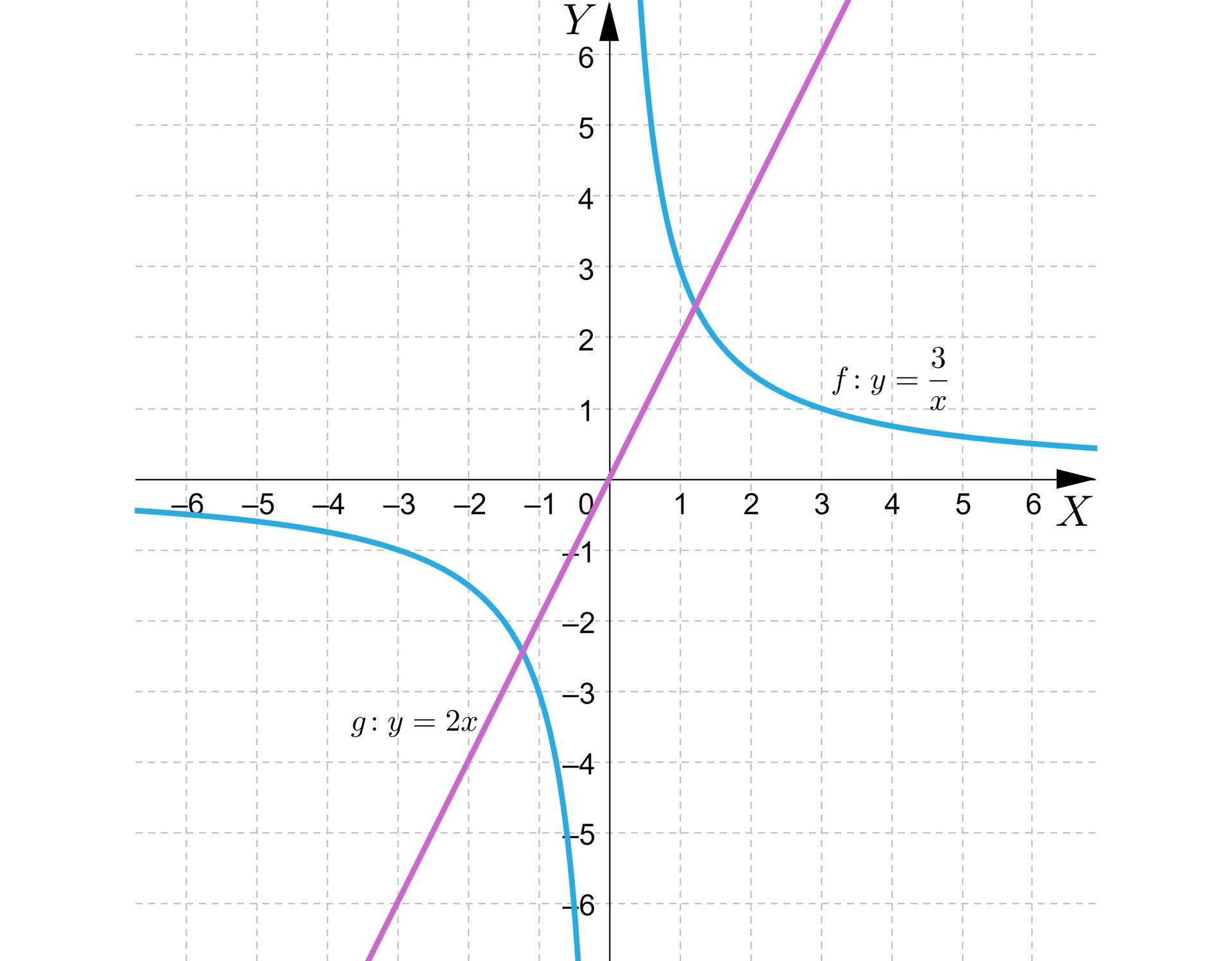

  Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus sześciu do sześciu, oraz z pionową osią $Y$ od minus sześciu do sześciu. Na płaszczyźnie narysowano wykres funkcji. f od x równa się 3 podzielić na x, której wykresem jest hiperbola, której gałęzie leżą w pierwszej i trzeciej ćwiartce układu współrzędnych i przechodzą przez punkty $\left(1;3\right)$, oraz $\left(-1;-3\right)$. Na wykresie poprowadzono prostą ukośną, będącą wykresem funkcji g od x równa się 2 x, przechodzącą przez początek układu współrzędnych oraz punkty $\left(1;2\right)$, oraz $\left(-1;-2\right)$. Prosta przecina obie gałęzie hiperboli.

  

  W tym przypadku wykresy funkcji mają zawsze dwa punkty wspólne, ponieważ „zajmują” te same ćwiartki układu współrzędnych.

Pozostaje rozważyć przypadek szczególny, tj.

• $b=1\Rightarrow f\left(x\right)=\frac{1}{x}$ oraz $g\left(x\right)=0$, wykresy funkcji nie mają punktów wspólnych.

  R1I8nf8AgmMW0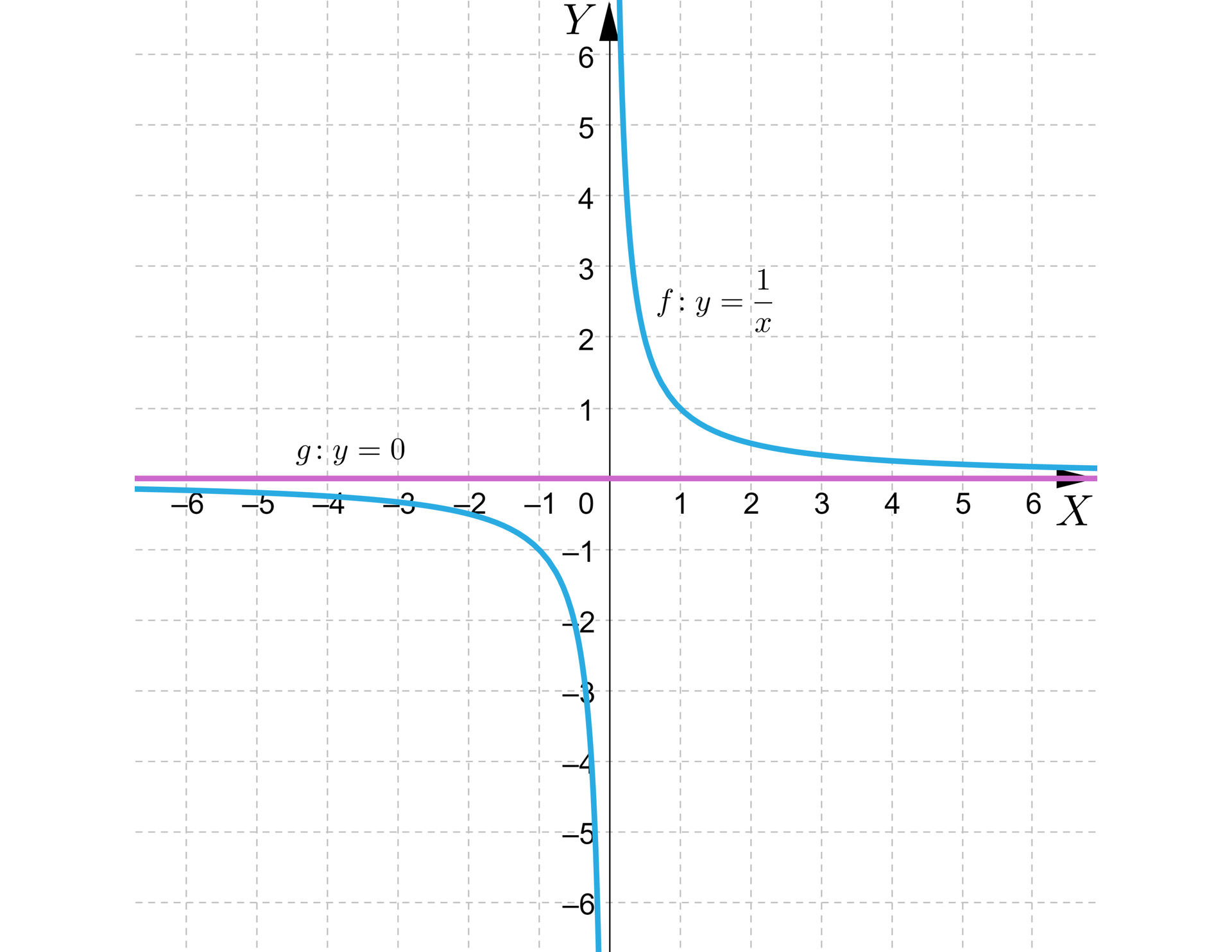

  Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus sześciu do sześciu, oraz z pionową osią $Y$ od minus sześciu do sześciu. Na płaszczyźnie narysowano wykres funkcji f od x równa się 1 podzielić na x, której wykresem jest hiperbola o gałęziach leżących w pierwszej i trzeciej ćwiartce układu współrzędnych. Przechodzą one przez punkty $\left(1;1\right)$, oraz $\left(-1;-1\right)$. Na wykresie poprowadzono poziomą prostą, która pokrywa się z poziomą osią $X$. Prosta jest wykresem funkcji g od x równa się 0 i nie ma punktów wspólnych z wykresem funkcji f.

  

Odpowiedź:

Wykresy funkcji $f\left(x\right)=\frac{b}{x}$, gdzie $x\ne 0, b\ne 0$ oraz $g\left(x\right)=\left(b-1\right)x$ nie mają punktów wspólnych dla $b\in \left(0,1\right.⟩$.

Dana jest funkcja wymierna $f\left(x\right)=\frac{kx+k^2-2}{x-k}$, gdzie $x\ne k, k\ne 0$. Pokażemy, dla jakich wartości parametru $k$ funkcja ta jest funkcją przedziałami malejącą, posiadającą ujemne miejsce zerowe.

Wykonamy przekształcenie wzoru funkcji do postaci kanonicznej:

$f\left(x\right)=\frac{kx+k^2-2}{x-k}=\frac{k\left(x-k\right)+2k^2-2}{x-k}=k+\frac{2k^2-2}{x-k}$

Aby funkcja ta była przedziałami malejąca, musi spełniać warunek:

$2k^2-2>0$

$k^2-1>0$

Stąd

$\left(k-1\right)\left(k+1\right)>0$

R1KvWC3kek6N1

Na ilustracji przedstawiono poziomą oś k, na której zaznaczono niezamalowany punkt -1, oraz niezamalowany punkt jeden. Na płaszczyźnie narysowano wykres funkcji, którym jest parabola o ramionach skierowanych do góry, przechodzących przez punkt minus jeden i jeden. Zaznaczono plusy nad osią $X$ poza obszarem paraboli.

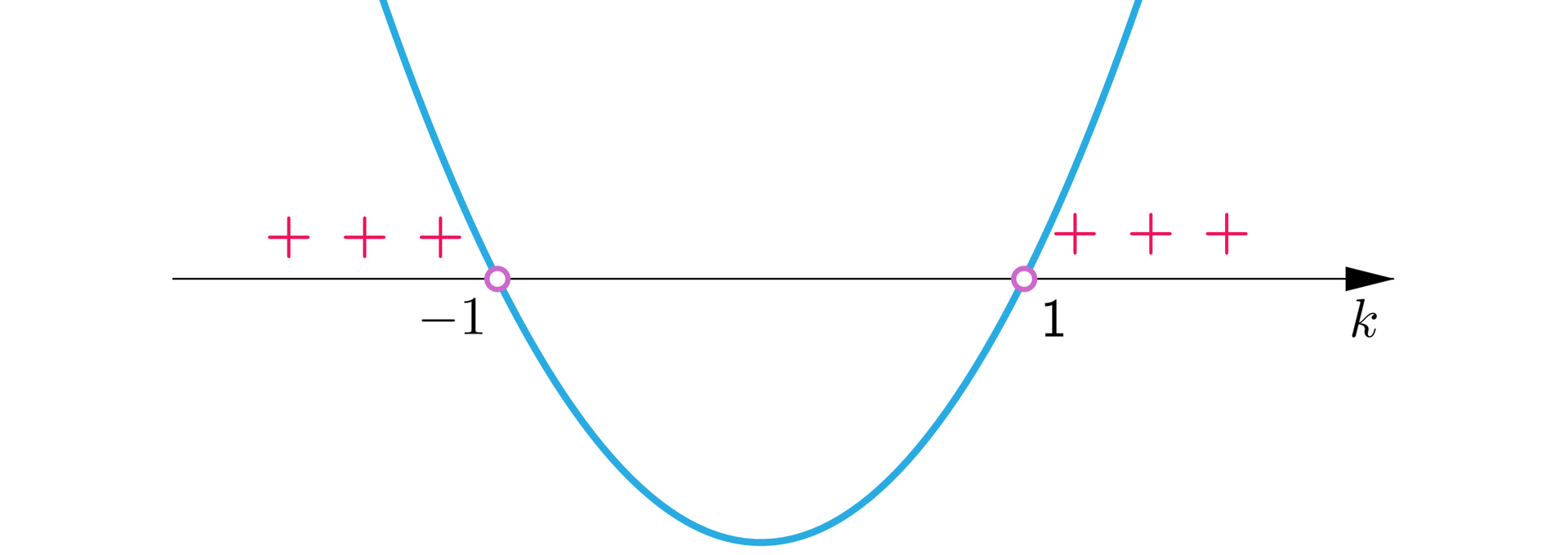
Zatem dla $k\in \left(-\infty ,-1\right)\cup \left(1,\infty \right)$ badana funkcja jest przedziałami  malejąca.

Zbadamy teraz dla jakich wartości parametru $k$ funkcja $y=f\left(x\right)$ posiada ujemne miejsce zerowe:

$f\left(x\right)=0\iff \frac{kx+k^2-2}{x-k}=0\iff kx+k^2-2=0$

$kx=2-k^2 |:k\ne 0$

$x=\frac{2-k^2}{k}$

$\frac{2-k^2}{k}<0$

$k\left(2-k^2\right)<0$

$k\left(\sqrt{2}-k\right)\left(\sqrt{2}+k\right)<0$

RPbHBiB8YBM23

Ilustracja przedstawia poziomą oś $k$, na której niezamalowanymi kółkami oznaczono następujące punkty od lewej: $-\sqrt{2}$, 0, $\sqrt{2}$. Na rysunku naniesiono wykres funkcji wielomianowej biegnący w następujący sposób: od minus nieskończoności do $-\sqrt{2}$, wykres biegnie niemal pionowo w dół, po czym przebija pod oś, gdzie początkowo biegnie w dół, a następnie odbija w górę i biegnie do punktu 0. W punkcie 0, wykres przebija nad oś i biegnie górę, po czym odbija w doł i biegnie do punktu $\sqrt{2}$. W punkcie $\sqrt{2}$ wykres przebija pod oś i biegnie niemal pionowo w dół do plus nieskończoności. Minusami zaznaczono przedział, w którym funkcja przyjmuje wartości ujemne, czyli przedział otwarty od $-\sqrt{2}$ do zera, oraz przedział otwarty od $\sqrt{2}$ do plus nieskończoności.

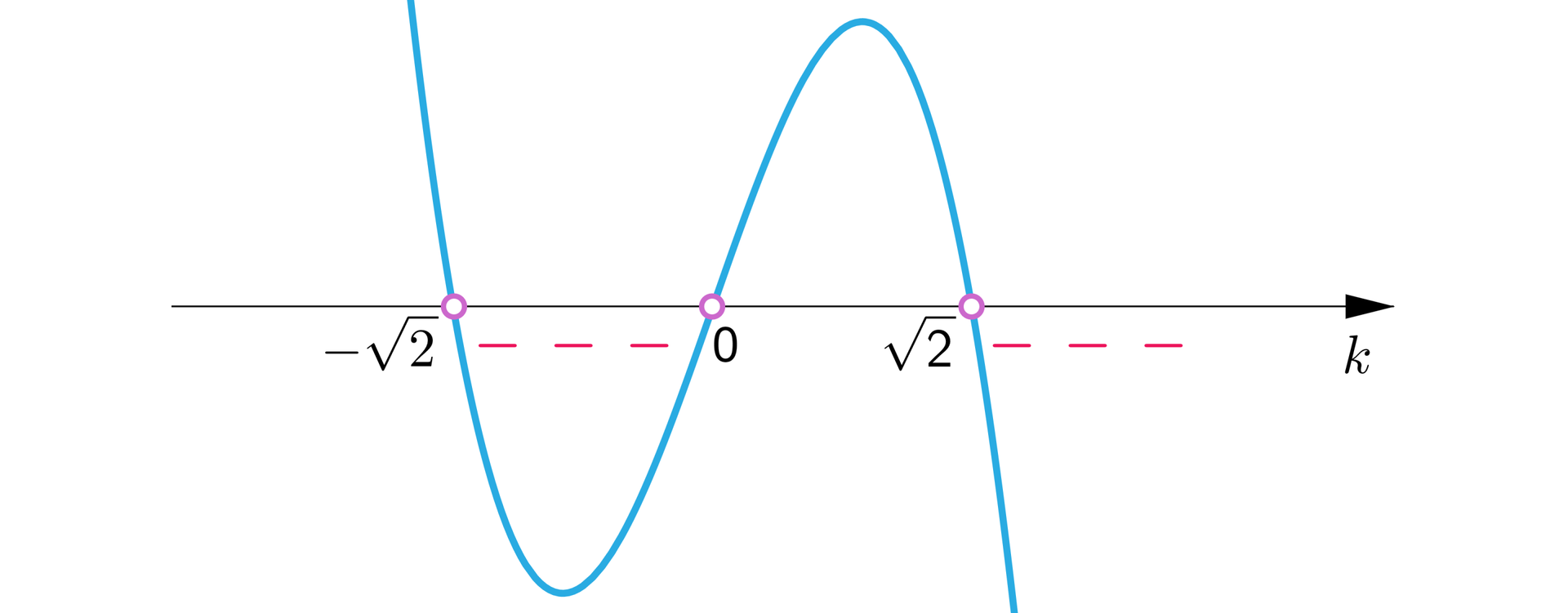
Zatem dla $k\in \left(-\sqrt{2},0\right)\cup \left(\sqrt{2},\infty \right)$ badana funkcja ma ujemne miejsce zerowe.

Pozostaje ustalenie, dla jakich wartości parametru $k$ spełnione są oba warunki:

RAv368lqG8Z0O

Na ilustracji przedstawiono wykres funkcji z poziomą osią $k$, na której zaznaczono punkty $-\sqrt{2}$, -1, zero, jeden, oraz $\sqrt{2}$. Nad wykresem zaznaczono poziomy odcinek i 3 poziome półproste symbolizujące pewne przedziały. Półprosta niebieska, biegnąca od minus nieskończoności do minus jeden, ograniczona jest z prawej strony niezamalowanym punktem. Jest to przedział otwarty od minus nieskończoności do minus jeden. Czerwony odcinek otwarty ograniczony lewostronnie niezamalowanym punktem o współrzędnej $-\sqrt{2}$ oraz ograniczonym prawostronnie niezamalowanym punktem o współrzędnej zero. Jest to interpretacja graficzna przedziału otwartego od minus pierwiastek kwadratowy z 2 do zera. Półprosta czerwona ograniczona lewostronnie niezamalowanym punktem o współrzędnej pierwiastek kwadratowy z dwóch reprezentuje zbiór otwarty od pierwiastka kwadratowego z 2 do plus nieskończoności. Półprosta niebieska ograniczona lewostronnie niezamalowanym punktem o współrzędnej 1 reprezentuje zbiór otwarty od jeden do plus nieskończoności.

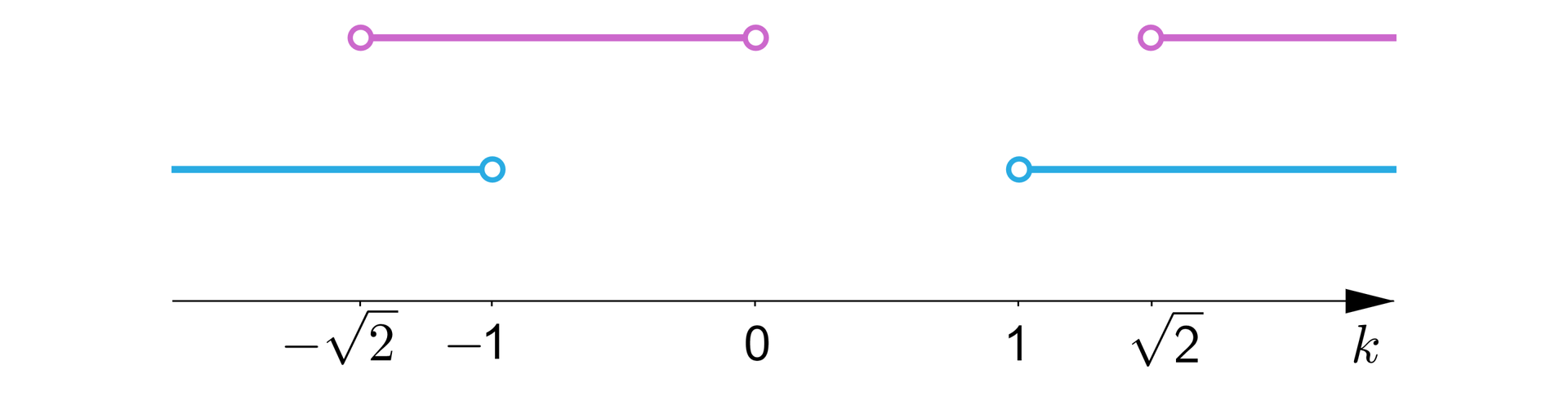
Odpowiedź:

funkcja $f\left(x\right)=\frac{kx+k^2-2}{x-k}$, gdzie $x\ne k$ jest funkcją  malejącą posiadającą ujemne miejsce zerowe dla $k\in \left(-\sqrt{2},-1\right)\cup \left(\sqrt{2},\infty \right)$.

dziedziną nierówności wymiernej $\frac{W\left(x\right)}{V\left(x\right)}>0$ lub $\frac{W\left(x\right)}{V\left(x\right)}<0$, lub $\frac{W\left(x\right)}{V\left(x\right)}\ge 0$, lub $\frac{W\left(x\right)}{V\left(x\right)}\le 0$ jest zbiór wszystkich liczb rzeczywistych z wyłączeniem pierwiastków wielomianu $V\left(x\right)$

liczbę $p$ nazywamy pierwiastkiem podwójnym (lub dwukrotnym) wielomianu $W\left(x\right)$ wtedy, gdy wielomian ten można przedstawić w postaci $W\left(x\right)={\left(x-p\right)}^2·Q\left(x\right)$, gdzie $Q\left(p\right)\ne 0$

liczbę $p$ nazywamy pierwiastkiem $k$-krotnym wielomianu $W\left(x\right)$ wtedy, gdy wielomian ten można przedstawić w postaci $W\left(x\right)={\left(x-p\right)}^k·Q\left(x\right)$, gdzie $Q\left(p\right)\ne 0$