Przeczytaj

W poniższych przykładach pokażemy, jak posługiwać się pojęciem wartości bezwzględnej w zadaniach dotyczących odległości liczb na osi liczbowej.

Przykład 1

Na osi liczbowejoś liczbowaosi liczbowej pewna liczba $a$ jest odległa od zera o $1, 5$ jednostki, a pewna liczba $b$ jest odległa od zera o $2$ jednostki. Jak daleko leży $a$ od $b$ ?

Zauważmy, że:

ponieważ liczba $a$ jest odległa od zera o $1, 5$ jednostki, więc $a = 1, 5$ lub $a = - 1, 5$ ,
ponieważ liczba $b$ jest odległa od zera o $2$ jednostki, więc $b = 2$ lub $b = - 2$ .

Zatem możliwe są dwa różne przypadki.

(1) Gdy obie liczby $a$ oraz $b$ leżą na osi liczbowejoś liczbowaosi liczbowej po tej samej stronie zera, ich odległość jest równa $0, 5$ .

R1Zqs4HEG7Fmq

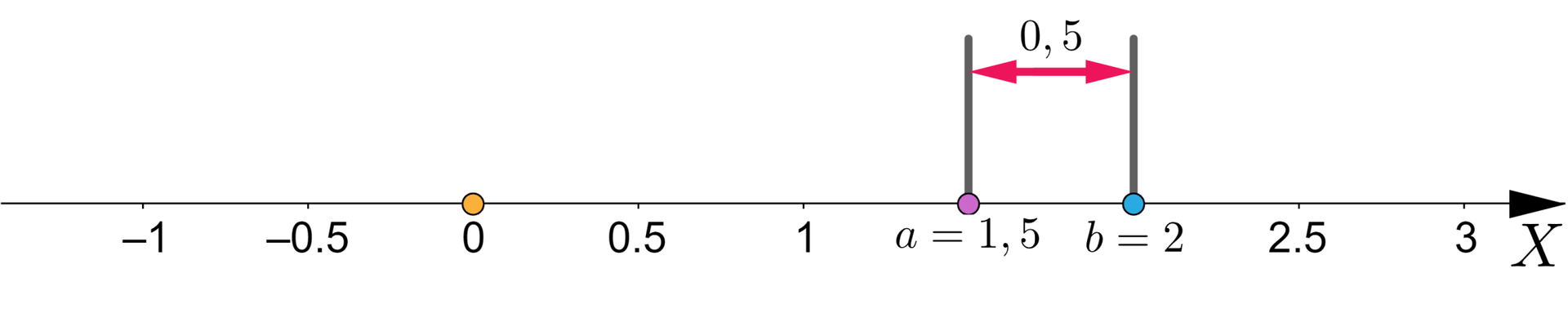
Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym pięć dziesiątych. Na osi zaznaczono liczby od minus jeden do trzech. Zaznaczono punkt a równy jeden i pół, oraz punkt b równy dwa. Odległość między punktem a i b wynosi pięć dziesiątych.

R1BnFcgrzbZ6H

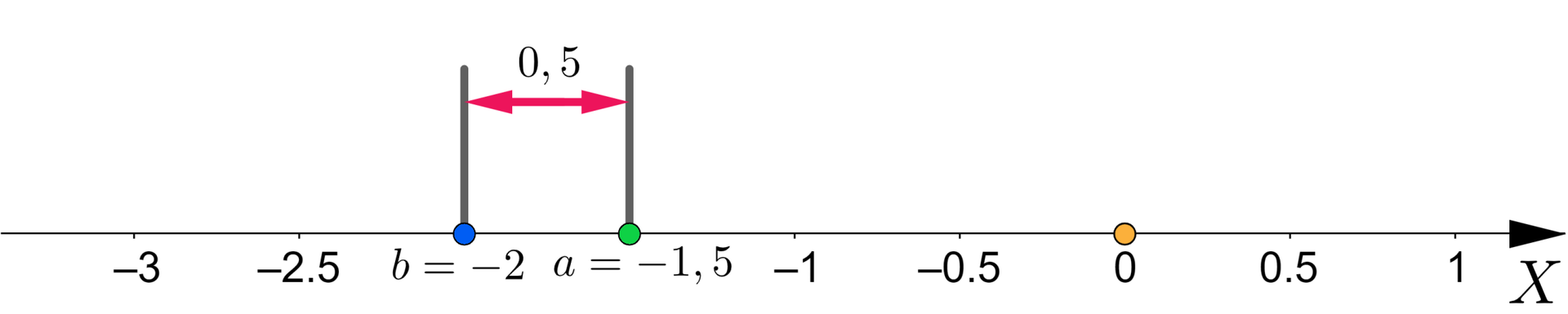
Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym pięć dziesiątych. Na osi zaznaczono liczby od minus trzech do jeden. Zaznaczono punkt a równy minus jeden i pół, oraz punkt b równy minus dwa. Odległość między punktem a i b wynosi pięć dziesiątych.

(2) Gdy liczby $a$ oraz $b$ leżą na osi liczbowejoś liczbowaosi liczbowej po przeciwnych stronach zera, ich odległość jest równa $3, 5$ .

R6XHPM8g5wSaF

Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym pięć dziesiątych. Na osi zaznaczono liczby od minus jeden i pół do dwóch i pół. Zaznaczono punkt a równy minus jeden i pół, oraz punkt b równy dwa. Odległość między punktem a i b wynosi trzy i pół.

RUGCHGp4kSIxD

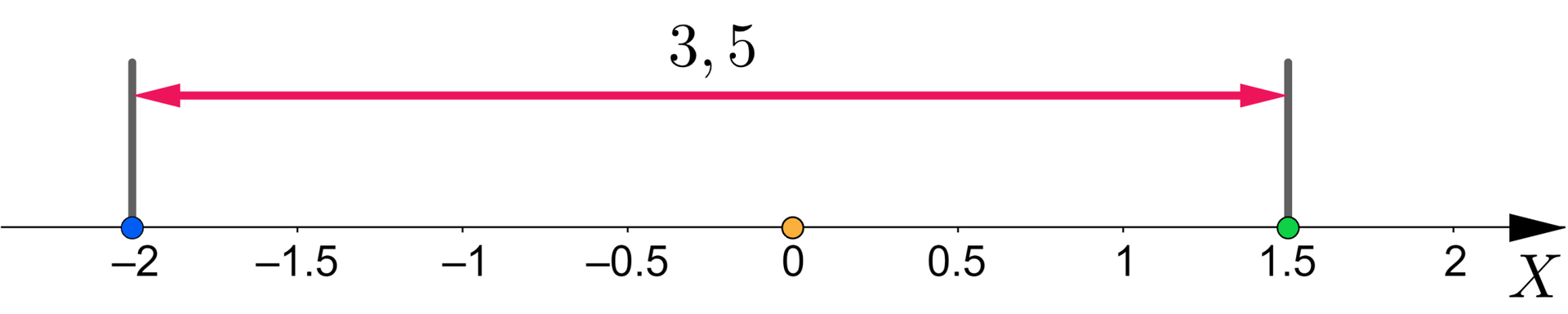
Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym pięć dziesiątych. Na osi zaznaczono liczby od minus dwóch do dwóch. Zaznaczono punkt a równy minus dwa, oraz punkt b równy jeden i pół. Odległość między punktem a i b wynosi trzy i pół.

Aby swobodnie formułować i rozwiązywać podobne zagadnienia, przypomnijmy definicję.

wartość bezwzględna liczby rzeczywistej

Definicja: wartość bezwzględna liczby rzeczywistej

Odległością liczby $x$ od zera nazywamy wartość bezwzględną liczby $x$ i oznaczamy symbolem $|x|$ .

Przykład 2

a) Liczba $6$ jest odległa od zera o sześć jednostek, a więc wartość bezwzględnawartość bezwzględna liczby $6$ jest równa $6$ .
Zatem prawdziwa jest równość $|6| = 6$ .

b) Liczba $- 3$ jest odległa od zera o trzy jednostki, zatem wartość bezwzględnawartość bezwzględna liczby $- 3$ jest równa $3$ . Oznacza to, że prawdziwa jest równość $|- 3| = 3$ .

Zauważmy, że:

jeżeli $x ⩾ 0$ , to $|x| = x$ ,
jeżeli $x < 0$ , to $|x| = - x$ .

Ważne!

Przyporządkowanie punktowi $A$ jego współrzędnej $a$ na osi liczbowejoś liczbowana osi liczbowej jest wzajemnie jednoznaczne, więc punkty i liczby będziemy utożsamiać, pisząc np.: $A = a$ . Podobnie, odległość między punktami $A = a$ oraz $B = b$ , będziemy też nazywać odległością między liczbami $a$ i $b$ .

Przykład 3

O liczbach z przykładu pierwszego można powiedzieć, że

$a$ jest rozwiązaniem równania $|x| = 1, 5$ ,
$b$ jest rozwiązaniem równania $|x| = 2$ .

Ważne!

Bezpośrednio z definicji wartości bezwzględnejwartości bezwzględnej wynikają następujące własności:
(1) $|x| ⩾ 0$ , dla dowolnej liczby rzeczywistej $x$ ,
(2) $|x| = |- x|$ , dla dowolnej liczby rzeczywistej $x$ ,
(3) $|x| = 0$ wtedy i tylko wtedy, gdy $x = 0$ .
(4) ${|x|}^{2} = x^{2}$ , dla dowolnej liczby rzeczywistej $x$ .

Ostatnią własność zapisujemy też w postaci równoważnej:
$\sqrt{x^{2}} = |x|$ , dla dowolnej liczby rzeczywistej $x$ .

Przykład 4

Wykażemy, że dla dowolnej dodatniej liczby rzeczywistej $x$ prawdziwa jest równość $|- 3 - |x + 1|| = x + 4$ .

Rozwiązanie

Korzystamy z własności wartości bezwzględnej.

Dla dowolnej liczby rzeczywistej $x$ prawdziwa jest nierówność $|x + 1| ⩾ 0$ , więc
$- |x + 1| ⩽ 0$
$- 3 - |x + 1| ⩽ - 3 < 0$ .
Stąd $|- 3 - |x + 1|| = - (- 3 - |x + 1|) = 3 + |x + 1|$ .
Ponadto dla $x > 0$ liczba $x + 1$ jest dodatnia, zatem prawdziwa jest równość $|x + 1| = x + 1$ .
Wobec tego $|- 3 - |x + 1|| = 3 + (x + 1) = x + 4$ .
W ten sposób dowód został zakończony.

Przykład 5

Obliczymy wartości wyrażenia $\sqrt{{(\sqrt{7} - 4)}^{2}}$ .

Rozwiązanie

Korzystamy z własności wartości bezwzględnej.

Ponieważ $\sqrt{7} < \sqrt{16} = 4$ , więc $\sqrt{7} - 4 < 0$ , co oznacza, że $|\sqrt{7} - 4| = - (\sqrt{7} - 4) = 4 - \sqrt{7}$ .
Wobec tego $\sqrt{{(\sqrt{7} - 4)}^{2}} = |\sqrt{7} - 4| = 4 - \sqrt{7}$ .

W ten sposób pokazaliśmy również, że liczba $4 - \sqrt{7}$ to odległość liczby $\sqrt{7} - 4$ od zera na osi liczbowej.

Uwaga. Korzystając ze wzoru skróconego mnożenia dostajemy
${(\sqrt{7} - 4)}^{2} = {\sqrt{7}}^{2} - 2 \cdot \sqrt{7} \cdot 4 + 4^{2} = 23 - 8 \sqrt{7}$ .
Zatem prawdziwa jest równość $\sqrt{23 - 8 \sqrt{7}} = 4 - \sqrt{7}$ .

Pokażemy teraz, jak znajdować odległość dwóch dowolnych liczb na osi liczbowejoś liczbowana osi liczbowej.

Przykład 6

Obliczymy odległość na osi liczbowejoś liczbowana osi liczbowej między punktami:
a) $A = - 5$ i $B = - 9$ ;
b) $C = 2$ i $D = - 4$ .

Rozwiązanie

a) Sporządzamy rysunek i liczymy jednostki.

R8frTqBoSjP5v

Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym jeden. Na osi zaznaczono liczby od minus jedenastu do minus trzech. Zaznaczono punkt A równy minus pięć, oraz punkt B równy minus dziewięć. Odległość między punktem A i B wynosi cztery.

Szukana odległość jest więc równa $4$ .

Odległość tę można obliczyć, odejmując od większej liczby (czyli $- 5$ ) mniejszą liczbę (czyli $- 9$ ):
$- 5 - (- 9) = - 5 + 9 = 4$ .

b) Sporządzamy rysunek i liczymy jednostki.

R1M580ZGHDVRA

Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym jeden. Na osi zaznaczono liczby od minus pięciu do trzech. Zaznaczono punkt C równy dwa, oraz punkt D równy minus cztery. Odległość między punktem C i D wynosi sześć.

Stwierdzamy, że szukana odległość jest równa $6$ .

Zauważmy, że odległość tę można obliczyć, odejmując od większej liczby (czyli $2$ ) mniejszą liczbę (czyli $- 4$ ):
$2 - (- 4) = 2 + 4 = 6$ .

Zliczanie jednostek na narysowanej osi jest skuteczne tylko w pewnych bardzo prostych przypadkach. Jeśli jednak mamy obliczyć odległość np. między liczbami $3 \frac{1}{5}$ oraz $- \sqrt{2}$ , to wynik musimy zostawić w postaci symbolicznej, jako różnicę między większą z tych liczb i mniejszą z nich:
$3 \frac{1}{5} - (- \sqrt{2}) = 3 \frac{1}{5} + \sqrt{2}$ .
Posługując się rozwinięciem dziesiętnym składników otrzymanej sumy możemy zapisać:
$3 \frac{1}{5} + \sqrt{2} = 4, 614 \dots$ ,
czyli rozpatrywana odległość jest liczbą z przedziału $(4, 5)$ .

Ogólną zasadę obliczania odległości liczb na osi opisuje poniższe twierdzenie.

Odległość liczb na osi liczbowej

Twierdzenie: Odległość liczb na osi liczbowej

Odległość dowolnych liczb rzeczywistych $x$ oraz $y$ na osi liczbowejoś liczbowana osi liczbowej jest równa wartości bezwzględnejwartości bezwzględnej ich różnicy:
$|x - y|$ .

Dowód

Dowód przeprowadzimy w trzech przypadkach.

(1) Jeśli $x = y$ , to zarówno odległość między $x$ i $y$ , jak i różnica $|x - y|$ są równe zeru, a więc zachodzi równość $|x - y| = x - y$ .

(2) Jeśli $x > y$ , to szukana odległość jest równa $x - y$ .
Wtedy też $x - y > 0$ , a więc zachodzi równość $|x - y| = x - y$ .

(3) Jeśli $y > x$ , to szukana odległość jest równa $y - x$ .
Zauważmy, że wtedy $x - y < 0$ , a więc $|x - y| = - (x - y) = y - x$ .
Oznacza to, że zachodzi równość: $|x - y| = y - x$ .

W ten sposób dowód został zakończony.

Powyższe spostrzeżenia dotyczące odległości liczb rzeczywistych na osi liczbowej warto zapisać w następującej postaci:

$|x - y| = \{\begin{cases} x - y, gdy x - y ⩾ 0 \\ y - x, gdy x - y < 0 \end{cases}$

Przykład 7

Obliczymy, jaka jest odległość na osi liczbowejoś liczbowaosi liczbowej między liczbami $k = 3$ oraz $n = 9$ .

Rozwiązanie

Odległość tę możemy obliczyć następująco:
$|n - k| = |9 - 3| = |6| = 6$ ,
ale też w taki sposób:
$|k - n| = |3 - 9| = |- 6| = 6$ .

Zatem liczba $k = 3$ jest odległa od liczby $n = 9$ o $6$ jednostek.

R10k2bEO9sGox

Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym jeden. Na osi zaznaczono liczby od dwóch do dziewięciu. Zaznaczono punkt k równy trzy, oraz punkt n równy dziewięć. Odległość między punktem k i n wynosi sześć.

Przykład 8

Odległość liczby $\frac{11}{47}$ od $- \sqrt{7}$ jest równa $|\frac{11}{47} - (- \sqrt{7})| = \frac{11}{47} + \sqrt{7}$ .
Ta odległość to liczba większa od $2$ i mniejsza od $3$ : $\frac{11}{47} + \sqrt{7} = 2, 879 \dots \in (2, 3)$ .

Przykład 9

Liczba $x + 5$ jest odległa od zera o $4$ jednostki. Ile jest równe $x$ ?

Rozwiązanie

$I$ sposób.
Ponieważ w odległości $4$ od zera są tylko dwie liczby: $4$ oraz $- 4$ , więc $x + 5 = 4$ lub $x + 5 = - 4$ .
Stąd $x = - 1$ lub $x = - 9$ .

$II$ sposób.
Ponieważ liczba $x + 5$ jest odległa od zera o $4$ jednostki, więc jest rozwiązaniem równania $| x + 5 | = 4$ .
Z własności wartości bezwzględnejwartości bezwzględnej otrzymujemy zatem, że
$x + 5 = 4$ lub $x + 5 = - 4$ .
Stąd $x = - 1$ lub $x = - 9$ .

Odp. Liczba $x$ jest równa $- 1$ lub jest równa $- 9$ .

Uwaga. Zapisując powyższe równanie w postaci
$|x - (- 5)| = 4$
możemy podać jeszcze inne zależności między liczbami z powyższego przykładu:

liczby $- 1$ oraz $- 9$ leżą na osi liczbowej w odległości $4$ od liczby $- 5$ ,
punkt $- 5$ jest środkiem odcinka o długości $8$ i końcach w punktach $- 1$ oraz $- 9$ .

RbKwAG37QsdGN

Na ilustracji przedstawiono oś liczbową o odcinku jednostkowym równym jeden. Na osi zaznaczono liczby od minus dziewięciu do minus jeden. Liczba minus dziewięć znajduje się w odległości czterech jednostek od liczby minus pięć. Liczba minus pięć znajduje się w odległości czterech jednostek od liczby minus jeden. Odległość całkowita między liczbą minus dziewięć a minus jeden wynosi osiem jednostek.

Pokażemy teraz, jak wykorzystać umiejętność obliczania odległości między punktami na osi liczbowej do znajdowania środka odcinka o końcach w tych punktach.

współrzędne środka odcinka na osi liczbowej

Twierdzenie: współrzędne środka odcinka na osi liczbowej

Jeżeli na osi liczbowej dane są punkty $A = a$ i $B = b$ , to środkiem odcinka $A B$ jest taki punkt $C = c$ , że:
$c = \frac{a + b}{2} .$

Dowód

Niech $A = a$ , $B = b$ i $C = c$ . Pokażemy, że punkt $c = \frac{a + b}{2}$ jest środkiem odcinka $A B$ . Zakładamy, że $|A C| = |C B|$ oraz $A \neq B$ .

Skoro $|A C| = |C B|$ , to $|a - c| = |c - b|$ . Rozwiążemy podaną równość z wartością bezwzględną. Rozpatrzymy cztery przypadki.

$1 °$ $a - c = - b + c$

$c = \frac{a + b}{2}$

$2 °$ $a - c = b - c$

$a = b$ - sprzeczność

$3 °$ $- a + c = b - c$

$c = \frac{a + b}{2}$

$4 °$ $- a + c = - b + c$

$a = b$ - sprzeczność

Gdy $a = b$ , to otrzymujemy sprzeczność. Zatem punkt $c = \frac{a + b}{2}$ jest środkiem odcinka $A B$ .

Przykład 10

Obliczymy współrzędną punktu $C$ , który jest środkiem odcinka $A B$ o końcach $A = - 2$ oraz $B = 4$ .

Rozwiązanie.

Korzystając z ustaleń poczynionych powyżej obliczamy:
$C = \frac{- 2 + 4}{2} = 1$ .

Uwaga. Ponieważ $|A B| = |4 - (- 2)| = 6$ , więc końce odcinka $A B$ leżą w odległości $\frac{6}{2} = 3$ od punktu $C$ . Wynika stąd, że rozwiązaniem równania $|x - 1| = 3$ są liczby $x = - 2$ oraz $x = 4$ .

Słownik

oś liczbowa

prosta, na której wyróżniono zwrot i punkt $O$ zwany zerowym oraz ustalono odcinek jednostkowy

wartość bezwzględna liczby rzeczywistej

Wartością bezwzględną liczby rzeczywistej $x$ nazywamy jej odległość na osi liczbowej od zera.
Wartość bezwzględną liczby $x$ oznaczamy symbolem $|x|$

Wprowadzenie

Test samosprawdzający

Słownik