FunkcjęfunkcjaFunkcję $f$ przedstawiono za pomocą grafu.

R1CedEVj7KmNH

Ilustracja przedstawia dwa zbiory X i Y. W zbiorze x znajdują się trzy liczby: 2, 5 oraz 11. W zbiorze y znajdują się liczby: 7, 8, 2, 9 oraz 6. Elementy zbiorów są połączone ze sobą strzałkami w następujący sposób: liczba 2 ze zbioru x jest połączona strzałką podpisaną literą f z liczbą 7 ze zbioru y. Liczba pięć ze zbioru x jest połączona strzałką z liczbą 8 ze zbioru y. Liczba 11 ze zbioru x jest połączona strzałką z liczbą 6 ze zbioru y.

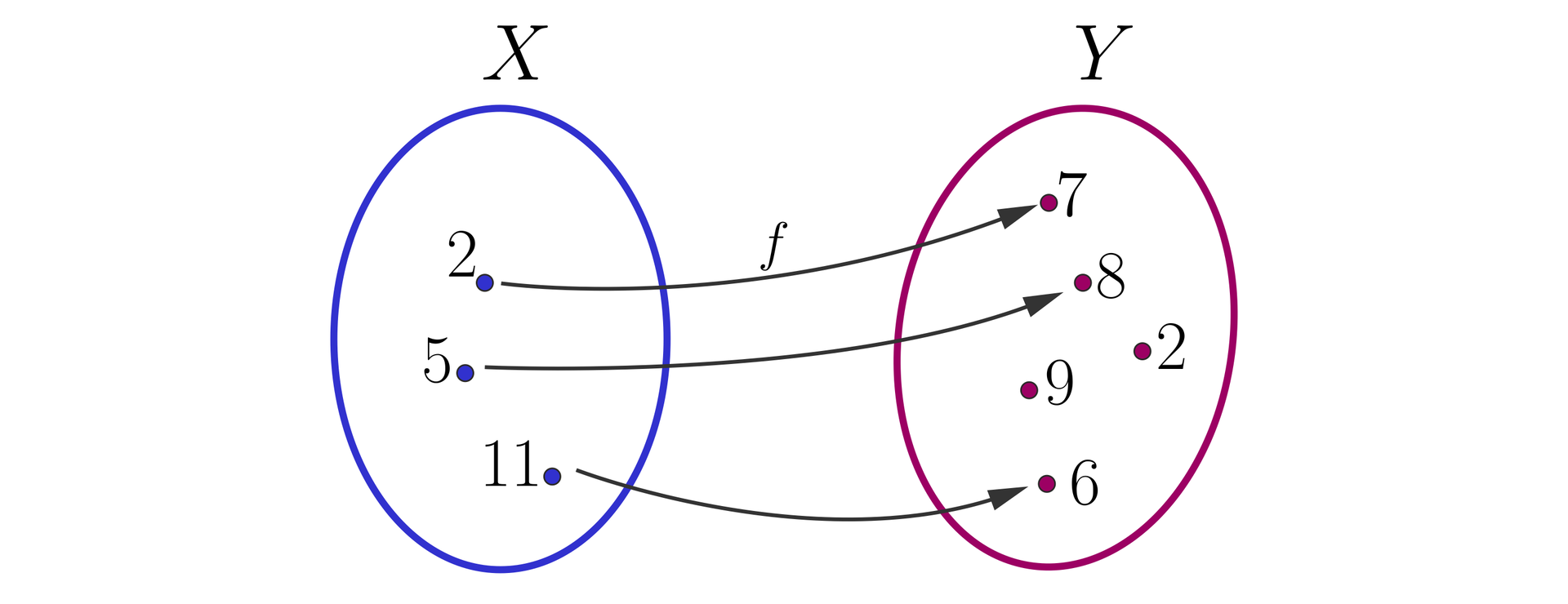
Dla jakiego argumentuargumentargumentu funkcja $f$ przyjmuje wartość $7$, a dla jakiego wartość $8$?

Rozwiązanie

Znajdujemy liczby $7$ i $8$ w zbiorze wartości i zauważamy, że prowadzą do nich strzałki, odpowiednio, od liczb $2$ i $5$. A zatem funkcja $f$ przyjmuje wartość $7$ dla argumentu $2$ oraz wartość $8$ dla argumentu $5$.

Na rysunku przedstawiono cały wykres funkcji $f$. Dla jakich argumentów funkcja $f$ przyjmuje wartość $2$?

RvAqwjzNDglCL

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 4 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji $y=f\left(x\right)$, który pojawia się na płaszczyźnie w trzeciej ćwiartce układu współrzędnych, biegnie ukośnie do punktu nawias minus dwa średnik dwa zamknięcie nawiasu, skąd dalej biegnie ukośnie do punktu nawias jeden średnik jeden zamknięcie nawiasu, dalej biegnie również ukośnie do punktu nawias trzy średnik trzy zamknięcie nawiasu, skąd biegnie ukośnie do punktu nawias cztery średnik dwa zamknięcie nawiasu.

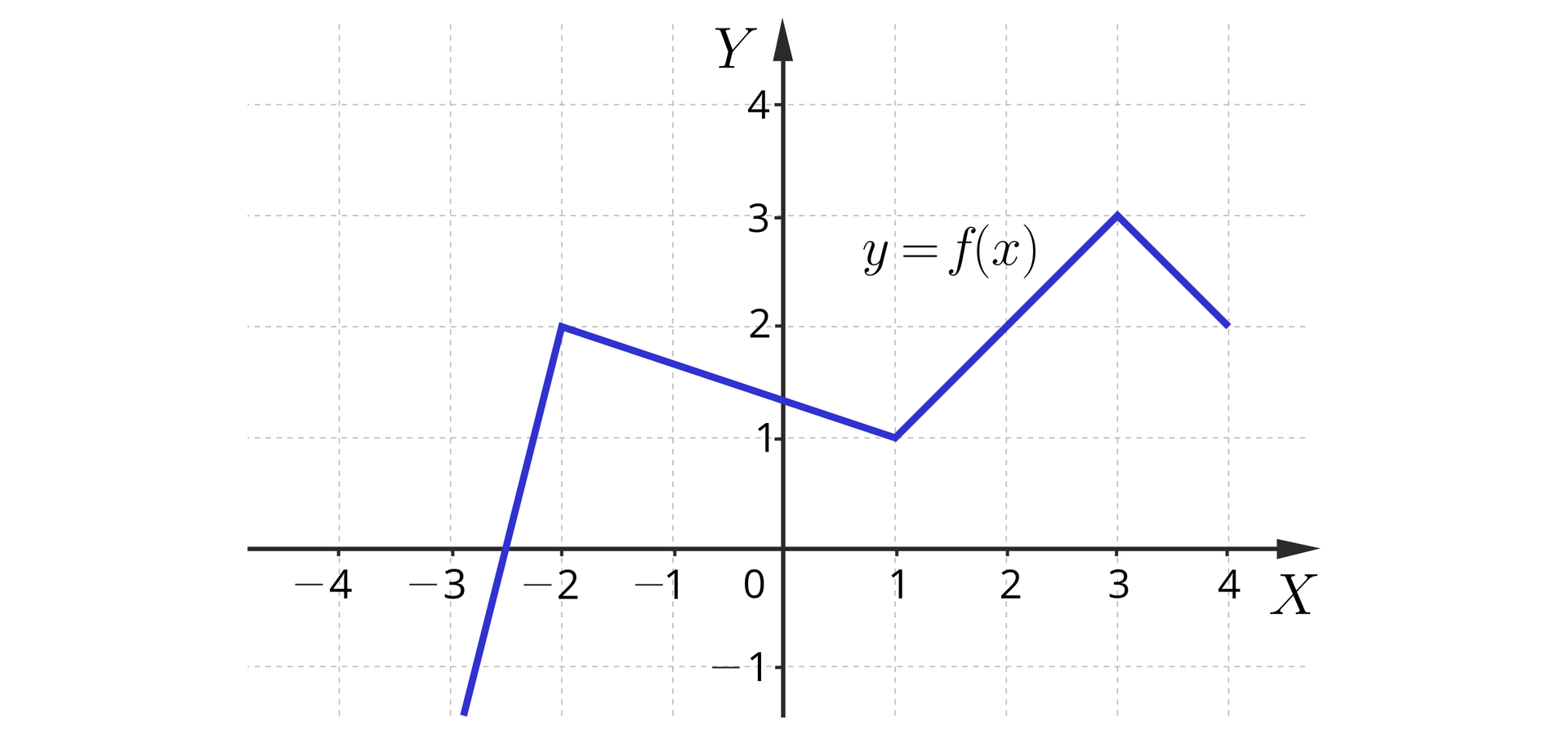
Rozwiązanie

Aby odpowiedzieć na pytanie dla jakich argumentów funkcja $f$ przyjmuje wartość $2$, narysujmy poziomą prostą o równaniu $y=2$.

RgUcceK0KtjpG

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 4 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji $y=f\left(x\right)$, który pojawia się na płaszczyźnie w trzeciej ćwiartce układu współrzędnych, biegnie ukośnie do punktu nawias minus dwa średnik dwa zamknięcie nawiasu, skąd dalej biegnie ukośnie do punktu nawias jeden średnik jeden zamknięcie nawiasu, dalej biegnie również ukośnie do punktu nawias trzy średnik trzy zamknięcie nawiasu, skąd biegnie ukośnie do punktu nawias cztery średnik dwa zamknięcie nawiasu. W układzie zaznaczono również poziomą prostą o równaniu $y=2$. Z punktów w których wykres $f\left(x\right)$ przecina się z tą prostą poprowadzono strzałki prowadzące do osi x. Zatem z punktu nawias minus dwa średnik dwa zamknięcie nawiasu poprowadzono pionową strzałkę do punktu nawias minus dwa średnik zero zamknięcie nawiasu. Z punktu nawias dwa średnik dwa zamknięcie nawiasu poprowadzono pionową strzałkę do punktu nawias dwa średnik zero zamknięcie nawiasu. Z punktu nawias cztery średnik dwa zamknięcie nawiasu poprowadzono pionową strzałkę do punktu nawias cztery średnik zero zamknięcie nawiasu.

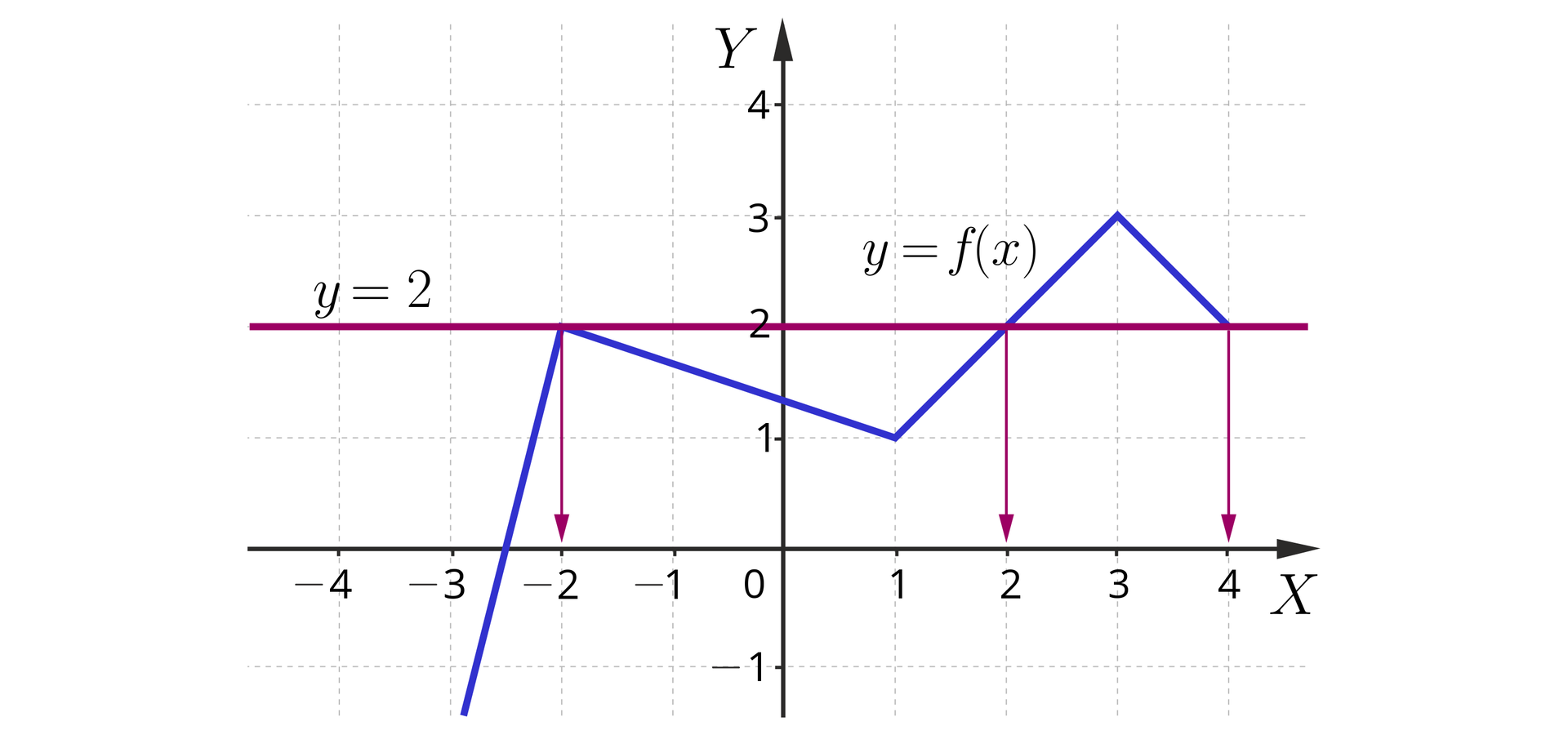
Przecina ona wykres funkcji $f$ w trzech punktach.

Przez te trzy punkty prowadzimy teraz pionowe proste, które przecinają oś $X$ w punktach: $x=-2$, $x=2$ oraz $x=4$.

Są to szukane argumenty, dla których funkcja $f$ przyjmuje wartość $2$.

Miejscem zerowym funkcji $f$ nazywamy taki argument $x_0$, dla którego funkcja przyjmuje wartość zero, tzn. zachodzi równość $f\left(x_0\right)=0$.

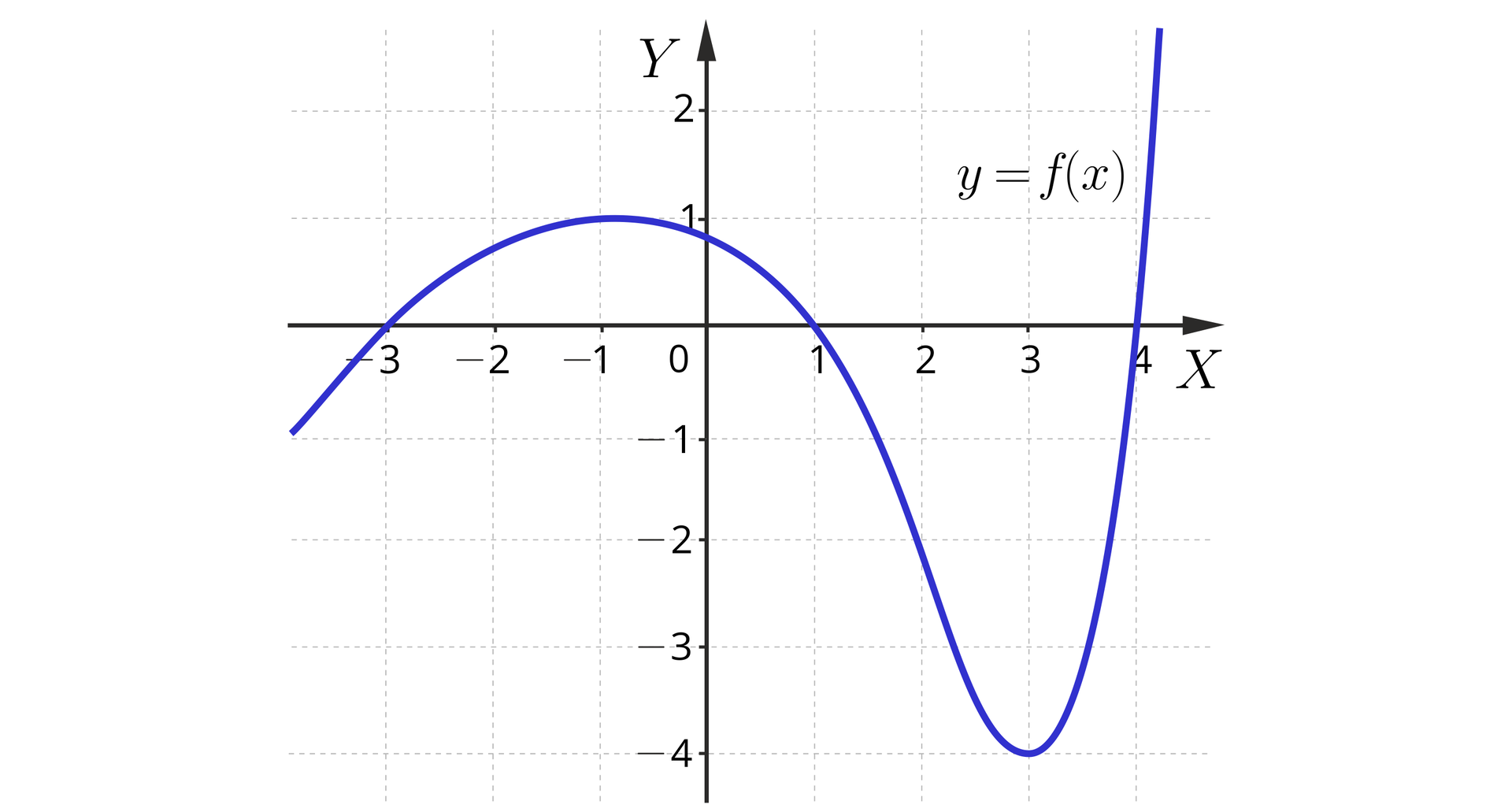
Na rysunku przedstawiony jest cały wykres funkcji $f$.

a) Odczytaj miejsca zerowe funkcji $f$.

b) Czy liczba $1$ należy do zbioru wartościzbiór wartości funkcjizbioru wartości tej funkcji?

R18wXQLNPL8rL

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 3 do 4 i pionową osią y od minus 4 do dwa. W układzie zaznaczono wykres funkcji $y=f\left(x\right)$, który pojawia się na płaszczyźnie w trzeciej ćwiartce układu, przecina oś x w punkcie nawias minus trzy średnik zero zamknięcie nawiasu, skąd biegnie po łuku do punktu nawias minus jeden nawias jeden zamknięcie nawiasu, skąd biegnie dalej po łuku przez punkt nawias dwa średnik minus dwa zamknięcie nawiasu do punktu nawias trzy średnik minus cztery. Dalej biegnie również po łuku przez punkt nawias cztery średnik zero zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce układu współrzędnych.

Rozwiązanie

(a) Odczytujemy z wykresu miejsca zerowe: $\left(-3\right)$, $1$ i $4$.

(b) Prowadzimy prostą poziomą o równaniu $y=1$ i zauważamy, że ma ona z wykresem funkcji punkty wspólne (dokładnie są dwa takie punkty). Zatem $1$ jest w zbiorze wartości funkcji $f$.

Obliczymy miejsca zerowe funkcji $f\left(x\right)=2x^2-162$.

Rozwiązanie

Mamy wyznaczyć takie argumenty $x$, dla których zachodzi równość $2x^2-162=0$. Wynika stąd, że $2x^2=162$, a więc $x^2=81$. Wobec tego $x=9$ lub $x=-9$.

Funkcja $f$ przypisuje każdej liczbie naturalnej sumę jej kwadratu i sześcianu. Czy wśród wartości tej funkcji znajduje się liczba $2$?

Rozwiązanie

Zauważmy, że $f\left(1\right)=1^2+1^3=1+1=2$. Zatem w zbiorze wartości funkcji $f$ jest liczba $2$.

Funkcja $f$ jest określona dla wszystkich liczb naturalnych $n$ wzorem $f\left(n\right)=3n^2+14$. Dla jakich argumentów funkcja ta przyjmuje wartość $206$?

Rozwiązanie

Szukamy takiej liczby naturalnej $n$, dla której zachodzi równość $3n^2+14=206$. Wobec tego $3n^2=192$, a więc $n^2=64$, czyli $n=\sqrt{64}=8$. Zatem jedynie dla $n=8$ funkcja $f$ przyjmuje wartość $206$.

Funkcja $g$ każdej liczbie naturalnej $n$ przypisuje kwadrat ostatniej cyfry jej zapisu dziesiętnego. Ustalimy, która z liczb: $2$, $3$, $4$, $5$ należy do zbioru wartości tej funkcji.

Rozwiązanie

Ponieważ ostatnią cyfrą liczby naturalnej może być $0$, $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$ lub $9$, więc w zbiorze wartości funkcji $g$ są wyłącznie kwadraty wymienionych $10$ liczb. Zatem spośród liczb $2$, $3$, $4$, $5$ jedynie $4=2^2$ należy do zbioru wartości funkcji $g$.

Funkcja $f$ przypisuje każdej liczbie dwucyfrowej iloczyn jej cyfr. Ustalimy, czy wśród wartości funkcji $f$ jest liczba:
a) $22$;
b) $24$;
c) $50$.

Rozwiązanie

Sprawdzamy, czy podane liczby można zapisać w postaci iloczynu dwóch liczb naturalnych mniejszych od $10$.

a) Ponieważ w rozkładzie na czynniki pierwsze liczby $22=2·11$ jest czynnik większy od $10$, więc wśród wartości funkcji $f$ nie ma liczby $22$;
b) Zauważamy np., że $24=3·8$, a więc $f\left(38\right)=24$, co oznacza, że wśród wartości funkcji $f$ jest liczba $24$;
c) W rozkładzie na czynniki pierwsze liczby $50=2·5·5$ są trzy czynniki mniejsze od $10$. Jednakże iloczyn obu możliwych do wyboru par tych czynników: $2·5=10$, $5·5=25$ tego warunku nie spełnia. Zatem wśród wartości funkcji $f$ nie ma liczby $50$.

Funkcja $f$ jest określona wzorem $f\left(x\right)=x^6+6x^3+9$ dla dowolnej dodatniej liczby rzeczywistej $x$. Dla jakiego argumentu ta funkcja przyjmuje wartość $900$?

Rozwiązanie

Mamy wyznaczyć dodatnią liczbę rzeczywistą $x$, dla której $x^6+6x^3+9=900$. Przekształcamy lewą stronę otrzymanego równania korzystając ze wzoru skróconego mnożenia na kwadrat sumy: $x^6+6x^3+9={\left(x^3\right)}^2+2·x^3·3+3^2={\left(x^3+3\right)}^2$.

Następnie zapisujemy równanie w postaci ${\left(x^3+3\right)}^2=900$.

Ponieważ liczba $x$ jest dodatnia, więc $x^3+3>0$, zatem z powyższego równania dostajemy $x^3+3=\sqrt{900}=30$, skąd $x^3=27=3^3$, czyli $x=3$.

Dziedziną funkcjidziedzina funkcjiDziedziną funkcji $f$ jest zbiór wszystkich liczb dwucyfrowych, których żadna cyfra nie jest zerem. Funkcja $f$ każdej liczbie z tego zbioru przypisuje sumę cyfr tej liczby podzieloną przez iloczyn jej cyfr. Ustal, czy wśród wartości tej funkcji jest liczba:
a) $2$;
b) $\frac{12}{27}$;
c) $\frac{3}{5}$.

Rozwiązanie

Oznaczamy: cyfrę jedności szukanej liczby przez $j$, cyfrę dziesiątek szukanej liczby przez $d$.

a) Szukamy takich liczb $j$ oraz $d$, których suma jest dwa razy większa od iloczynu. Zauważamy, że warunek ten spełniają np. liczby $j=d=1$. Zatem $f\left(11\right)=2$, a więc wśród wartości tej funkcji jest liczba $2$;
b) Szukając rozkładu liczby $27$ na takie dwa czynniki $j$ oraz $d$, których suma jest równa $12$ znajdujemy parę $j=3$, $d=9$. Zatem $f\left(93\right)=\frac{3+9}{3·9}=\frac{12}{27}$, a więc wśród wartości tej funkcji jest liczba $\frac{12}{27}$
c) Załóżmy, że istnieją takie liczby $j$ oraz $d$, które spełniają równanie $\frac{j+d}{j·d}=\frac{3}{5}$. Wtedy $3jd=5\left(j+d\right)$, a więc $3jd-5j-5d=0$. Otrzymane równanie możemy przekształcić równoważnie, otrzymując kolejno:

$9jd-15j-15d=0$

$9jd-15j-15d+25=25$

$\left(3j-5\right)·\left(3d-5\right)=25$

Wynika stąd, że liczbę $25$ da się przedstawić w postaci iloczynu dwóch czynników całkowitych $3j-5$ oraz $3d-5$. Sprawdzamy, że jest to możliwe jedynie w dwóch przypadkach:
(1) gdy $3j-5=5$ i $3d-5=5$
lub
(2) gdy jedna z liczb $3j-5$, $3d-5$ jest równa $25$ i jednocześnie druga jest równa $1$.

W przypadku (1) otrzymujemy $j=d=\frac{10}{3}$ - te wartości nie spełniają warunków zadania.

W przypadku (2) otrzymujemy, że jedna z liczb $j$, $d$ byłaby rozwiązaniem równania $3t-5=25$, a więc miałaby wartość $10$, czyli nie spełniałaby warunków zadania.

Oznacza to, że wśród wartości tej funkcji nie ma liczby $\frac{3}{5}$.

Funkcja $f$ dla każdej liczby $x\ne -1$ spełnia warunek $f\left(\frac{x-4}{x+1}\right)=x^2+1$. Dla jakiego argumentu funkcja ta osiąga wartość $2$?

Rozwiązanie

Ponieważ wartość funkcji $f$ opisana jest przez wyrażenie $x^2+1$, więc najpierw obliczamy dla jakiego $x$ zachodzi równość $x^2+1=2$.

Otrzymujemy stąd, że $x^2=1$, czyli (wobec poczynionego zastrzeżenia $x\ne -1$) otrzymujemy, że $x=1$.

Ponieważ argument funkcji $f$ opisany jest przez wyrażenie $\frac{x-4}{x+1}$, więc dla $x=1$ otrzymujemy $\frac{1-4}{1+1}=-\frac{3}{2}$.

Wynika stąd, że funkcja $f$ osiąga wartość $2$ dla argumentu $-\frac{3}{2}$.

zmienna niezależna funkcji będąca elementem jej dziedziny

zbiór wszystkich argumentów funkcji

przyporządkowanie elementom jednego zbioru $X$ elementów drugiego zbioru $Y$ w taki sposób, że każdemu elementowi $x\in X$ odpowiada dokładnie jeden element $y\in Y$

zbiór liczb, które są wartościami dla argumentów funkcji