Przeczytaj
Sporządzając wykres funkcji linowej (czyli rysując prostą) wybieramy dowolne liczby oraz z dziedzinydziedziny tej funkcji i obliczamy dla nich wartości funkcji oraz a następnie łączymy otrzymane punkty. W sytuacji gdy wykres funkcji jest sumą odcinków lub półprostych określonych za pomocą funkcji liniowych , , , , sporządzamy w tym samym układzie współrzędnych wykresy funkcji , , , , w przedziałach, w których są one określone.
Sporządzimy wykres funkcji , gdzie – część całkowita liczby .
Część całkowita (cecha) dowolnej liczby jest to największa liczba całkowita nie większa od .
Funkcja – część całkowita określona jest na zbiorze liczb rzeczywistych i przyjmuje w przedziałach dla wartość .
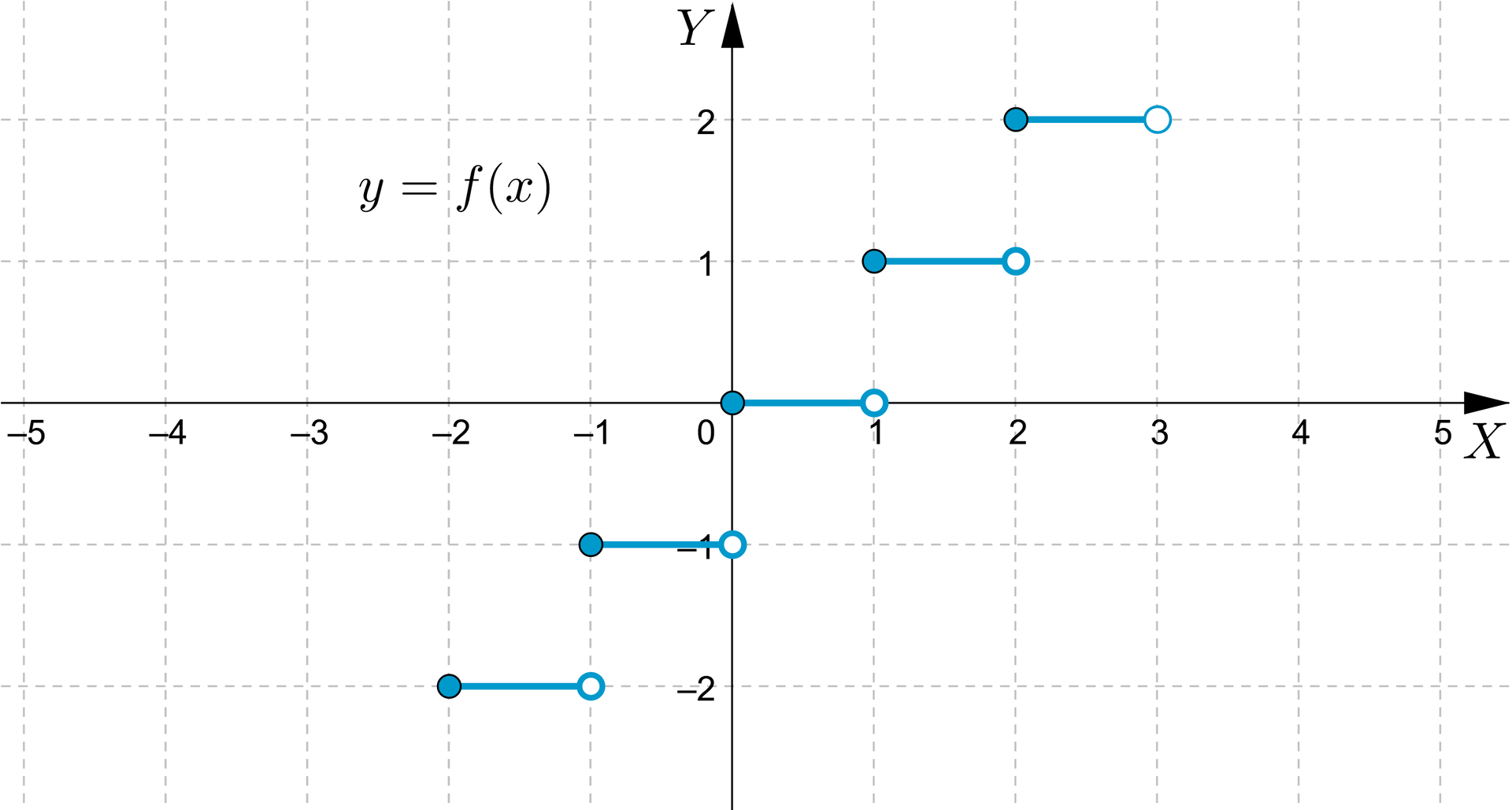
Zauważmy, że wykres składa się z rozłącznych odcinków długości , przy czym lewy koniec każdego odcinka należy do wykresu a prawy do niego nie należy.
DziedzinąDziedziną tej funkcji jest zbiór liczb rzeczywistych, zbiorem wartości funkcjizbiorem wartości funkcji jest zbiór liczb całkowitych, funkcja przyjmuje wartość zero dla każdego argumentu z przedziału .
Sporządzimy wykres funkcji .
Funkcja tej postaci nazywana jest częścią ułamkową lub mantysą. Obliczmy dla kilku argumentów, wartości funkcji.
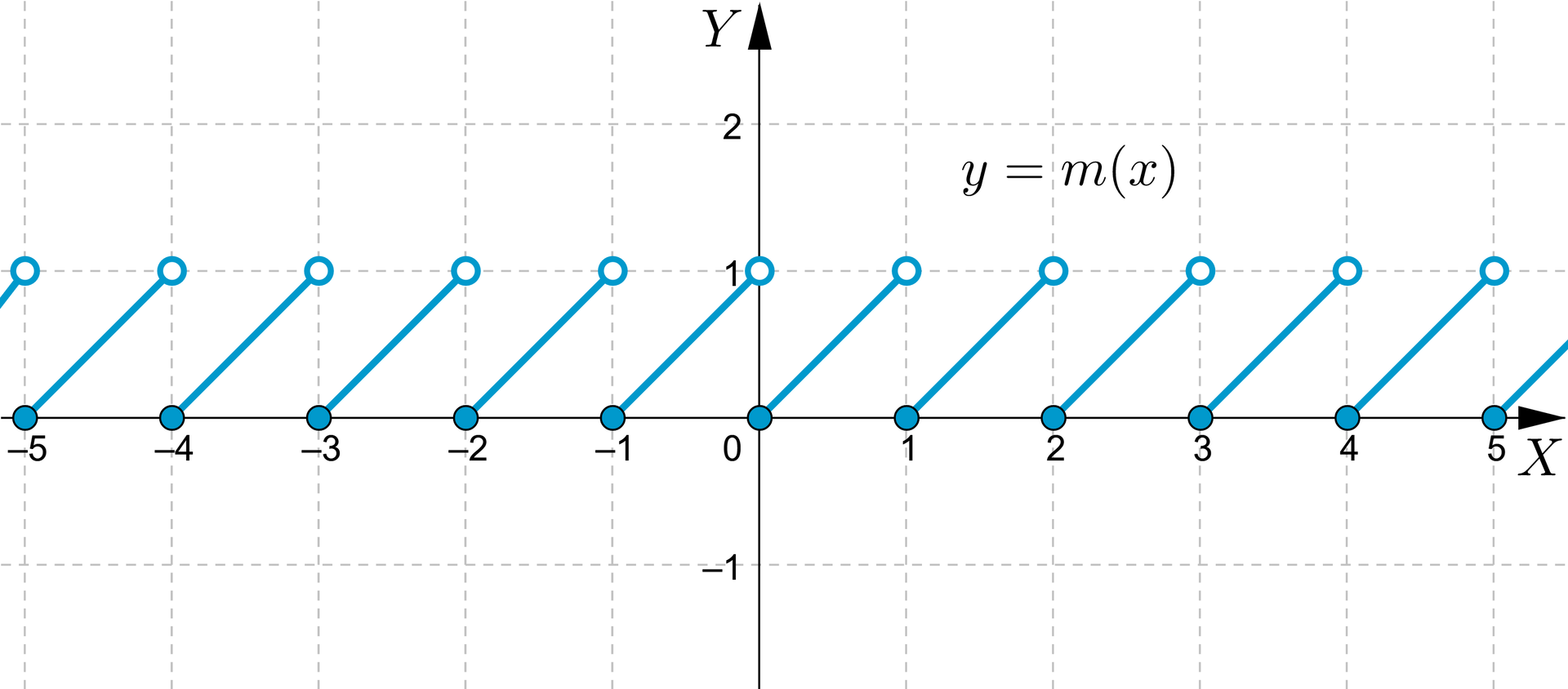
DziedzinąDziedziną tej funkcji jest zbiór liczb rzeczywistych, zbiorem wartościzbiorem wartości tej funkcji jest przedział lewostronnie domknięty . Funkcja jest przedziałami rosnąca, tzn. jest rosnąca w każdym przedziale , gdzie . Ma nieskończenie wiele miejsc zerowych , gdzie .
Narysujemy wykres funkcji
.
Funkcję nazywamy funkcją „znak ” ( jest skrótem łacińskiego słowa signum, czyli znak). Sporządzamy w tym samym układzie współrzędnych wykresy funkcji:
w przedziale wykres funkcji ,
w przedziale rysujemy wykres funkcji ,
dla funkcja przyjmuje wartość .
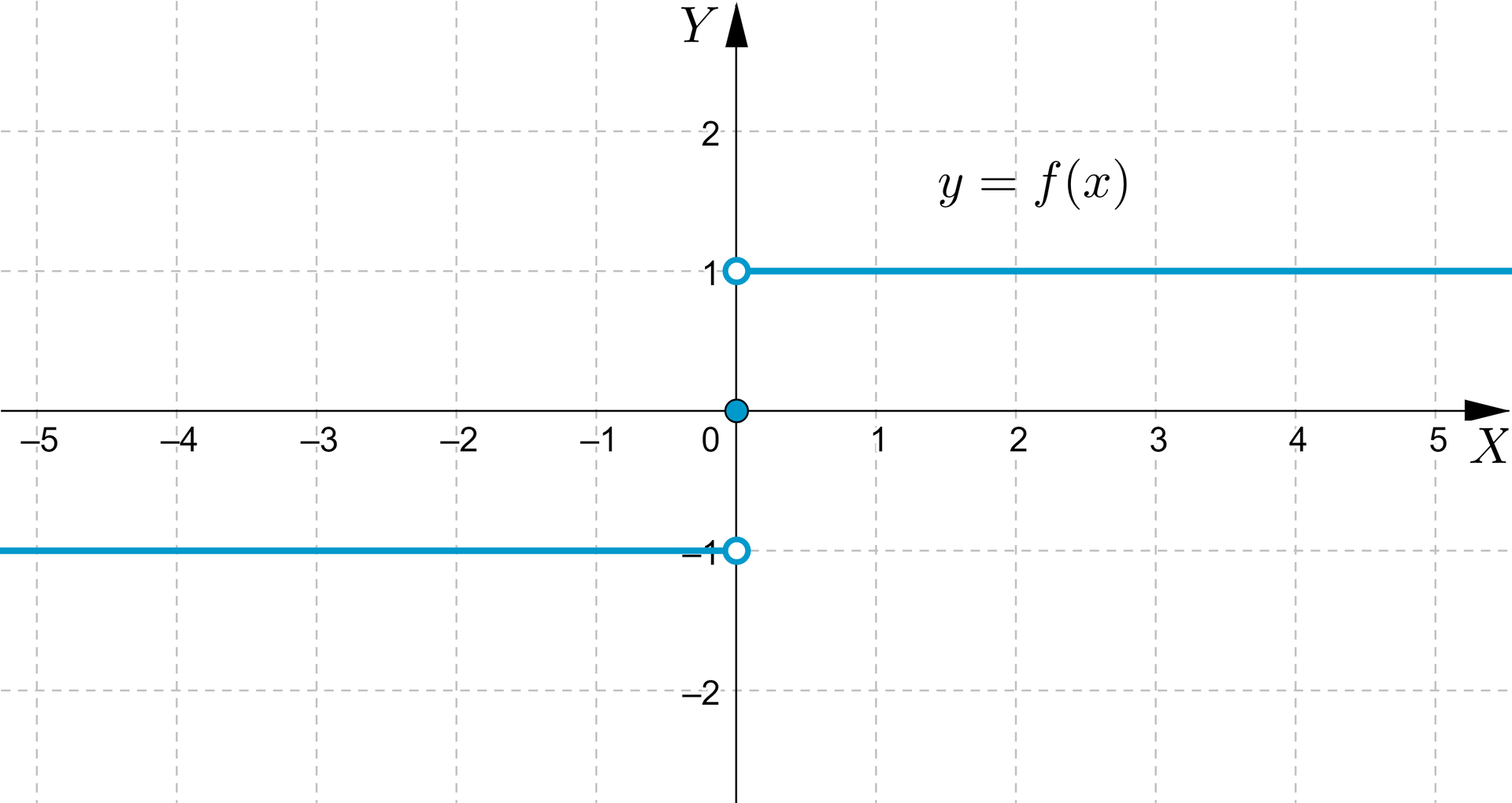
Sporządzimy wykres funkcji określonej wzorem:
,
a następnie odczytamy z wykresu: dziedzinędziedzinę, zbiór wartościzbiór wartości, miejsca zerowe funkcji. Określimy przedziały, w których funkcja jest malejąca.
Sporządzamy w tym samym układzie współrzędnych wykresy funkcji.
, gdy , , .
, gdy , , dla każdego .
, gdy , , .
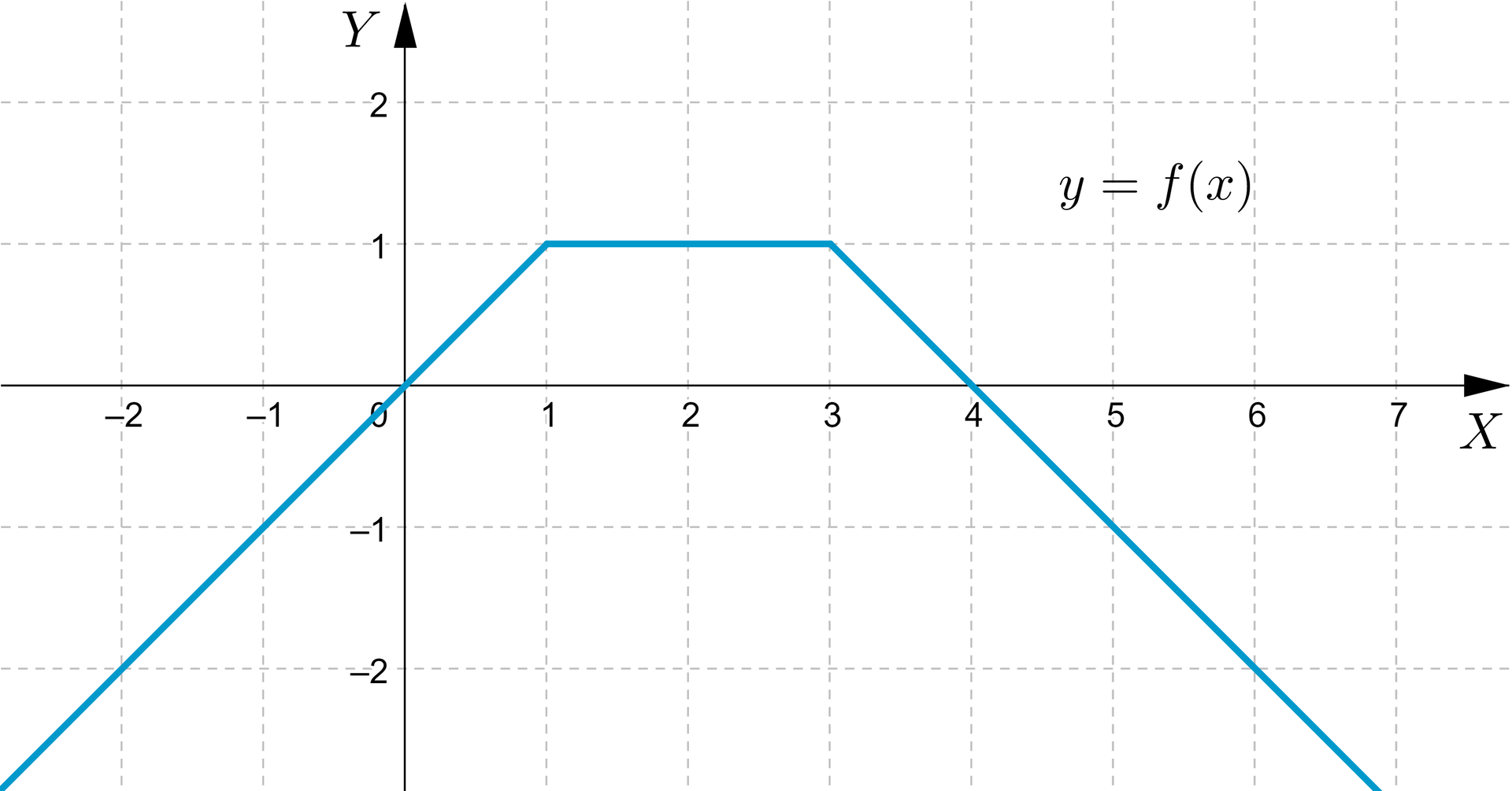
dziedzina funkcjidziedzina funkcji:
zbiór wartości funkcjizbiór wartości funkcji:
dla i
funkcja jest malejąca w przedziale
Sporządzimy wykres funkcji określonej wzorem
,
a następnie odczytamy z wykresu: dziedzinędziedzinę, zbiór wartościzbiór wartości, miejsca zerowe funkcji.
Sporządzamy w tym samym układzie współrzędnych wykresy funkcji:
w przedziale wykres funkcji ; w tym celu obliczymy wartości ,
w przedziale wykres funkcji stałej
w przedziale rysujemy wykres funkcji ; w tym celu obliczymy wartości ,
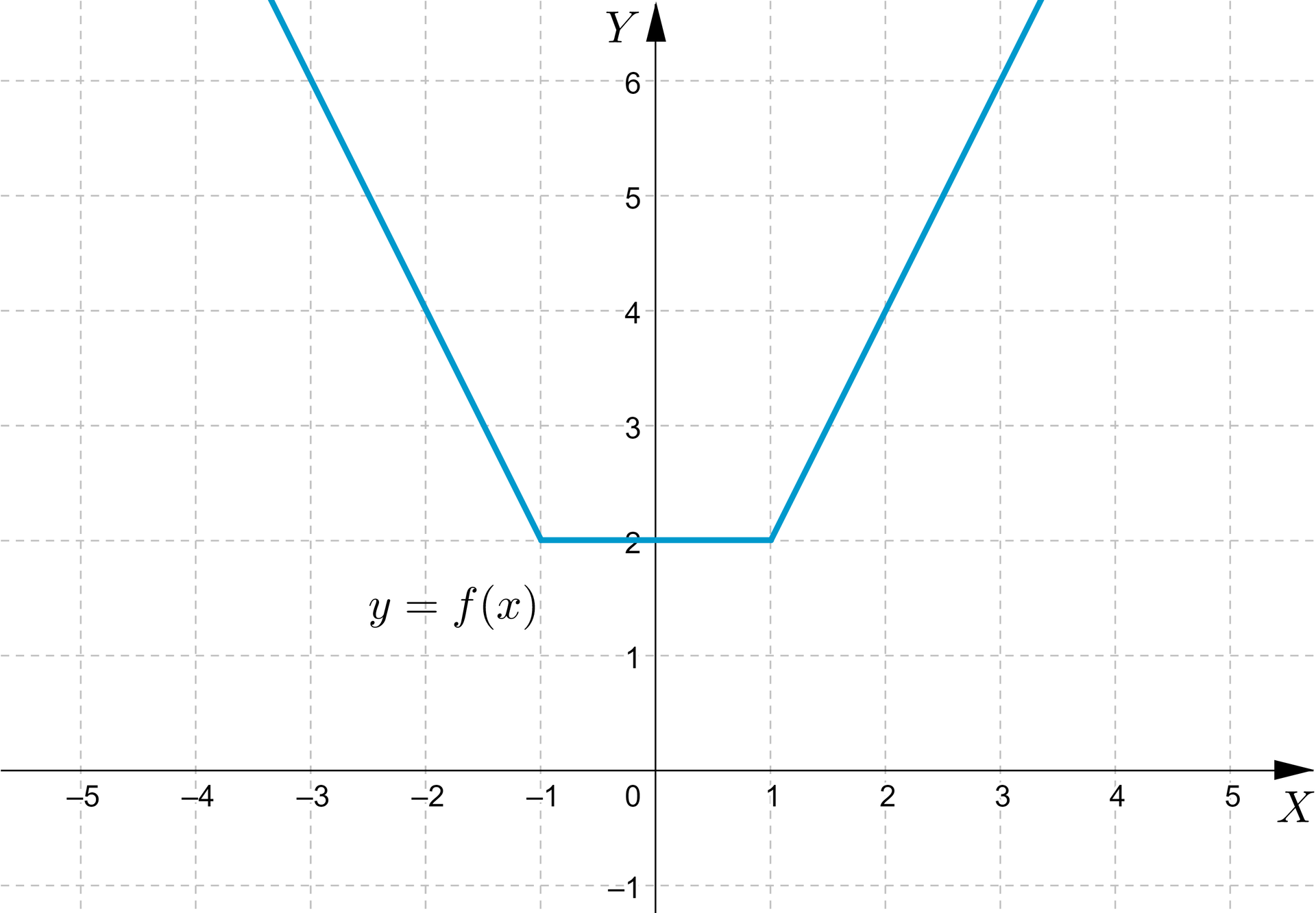
dziedzina funkcjidziedzina funkcji:
zbiór wartości funkcjizbiór wartości funkcji:
funkcja nie ma miejsc zerowych
Na podstawie wykresu funkcji określimy wzór funkcji.
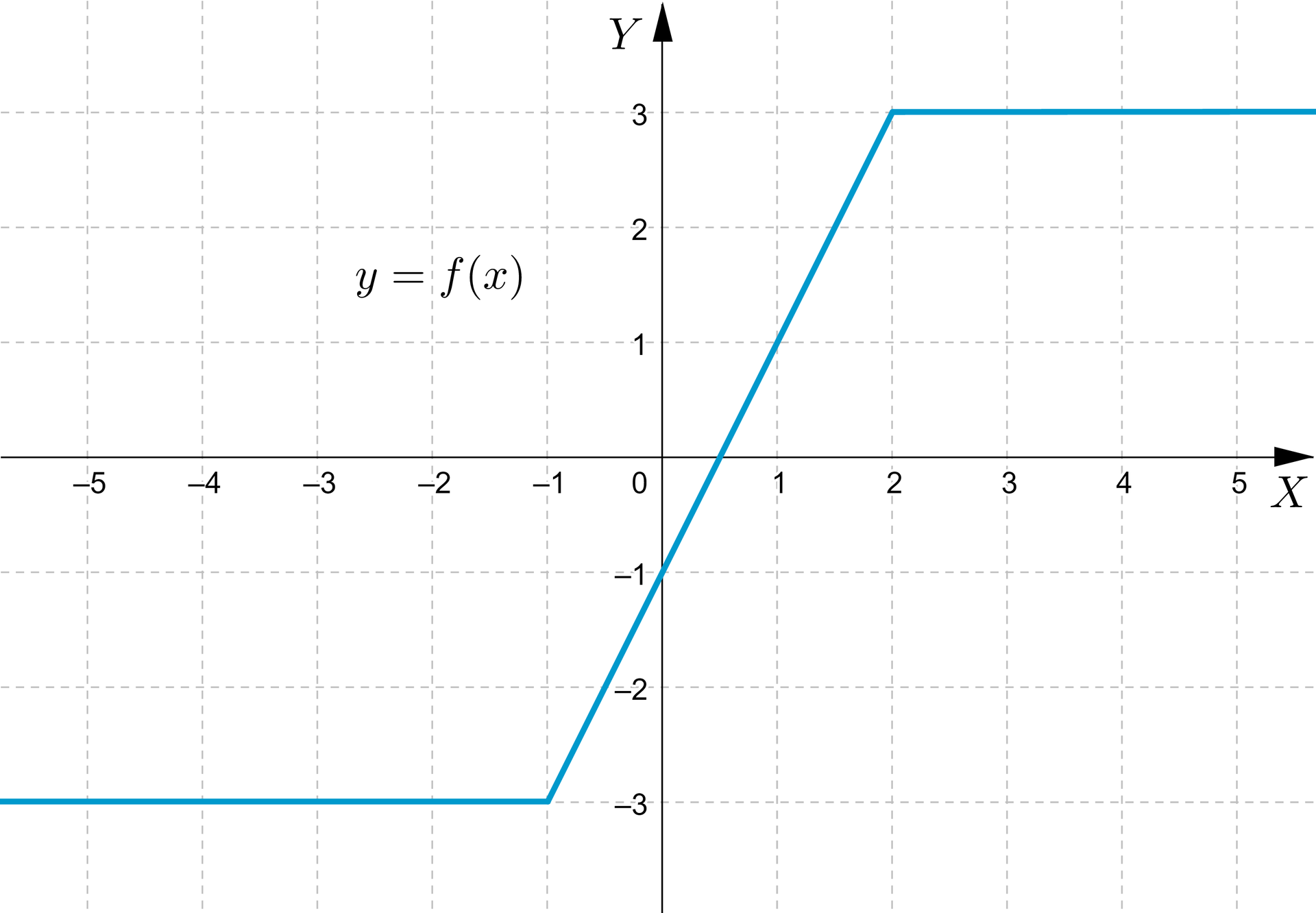
Szukamy wzoru funkcji w przedziałach:
w przedziale funkcja przyjmuje jedną wartość równą : ,
w przedziale wykres funkcji jest prostą,która zawiera punkt , więc i równanie tej prostej możemy zapisać jako: ; odczytujemy z wykresu współrzędne kolejnego punktu: i podstawiamy do równania prostej:
,
stąd i ,
w przedziale funkcja przyjmuje jedną wartość równą : .
Szukany wzór funkcji jest następujący:
.
Słownik
zbiór wszystkich wartości zmiennej niezależnej, dla których funkcja jest określona
zbiór wszystkich , dla których istnieje taki argument należący do dziedziny funkcji , że .