Dany jest graniastosłup prawidłowy trójkątny o objętości $4 {\mathrm{cm}}^3$. Wyznaczymy długość krawędzi podstawy, dla której pole powierzchni całkowitej jest najmniejsze z możliwych.

Rozwiązanie

Niech $a$ będzie krawędzią podstawy oraz $H$ wysokością graniastosłupa.

RWqYrC4Pxir6H

Ilustracja graniastosłup o podstawie będącej trójkątem równobocznym o boku a. Wysokość bryły wynosi H.

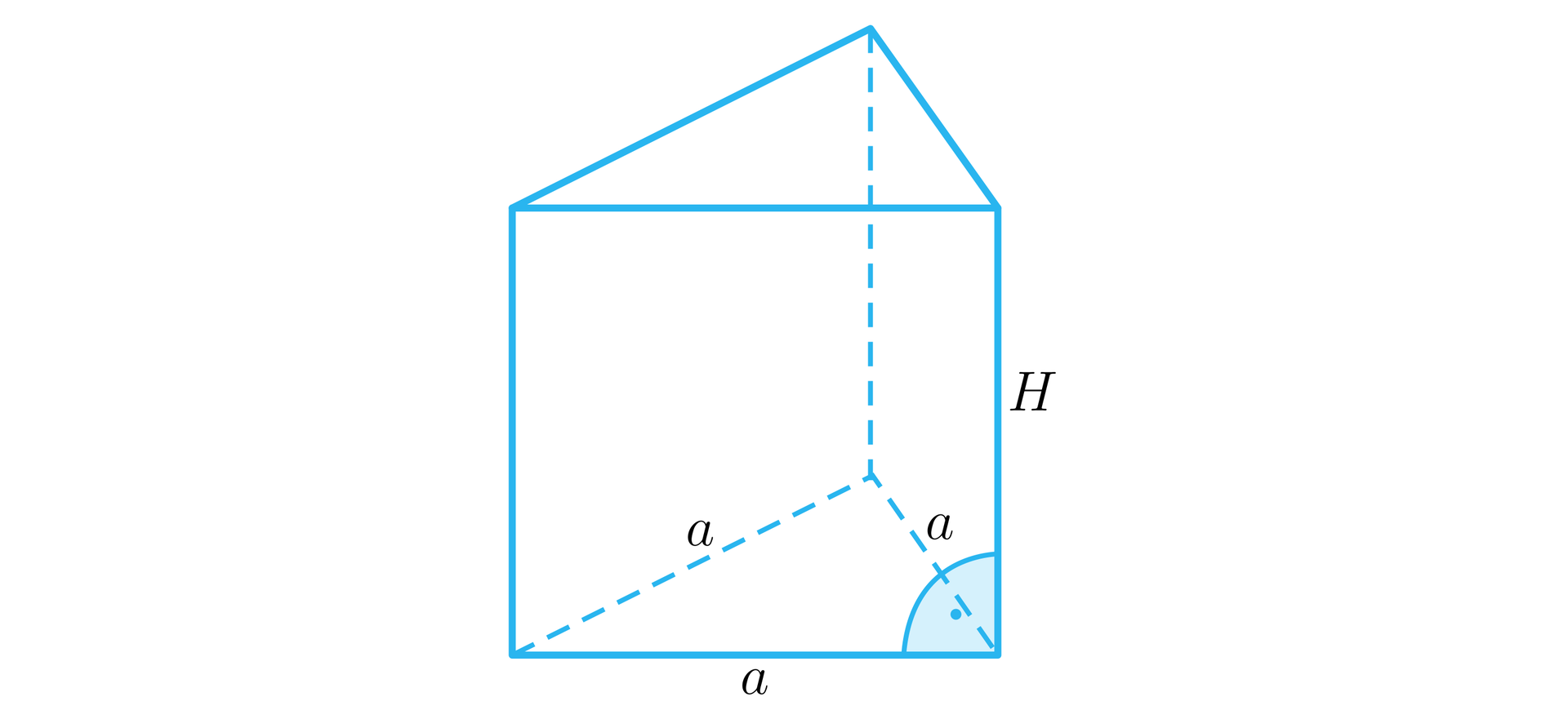
Ze wzoru na objętość graniastosłupa $V=P_p·H$ otrzymujemy $4=P_p\cdot H$. Ponieważ $P_p=\frac{a^2\sqrt{3}}{4}$ otrzymujemy, że $H=\frac{16\sqrt{3}}{3a^2}$.

Zapiszmy wzór na pole całkowite

$P_c=2P_p+P_b$.

Podstawiając

$P_c=\frac{a^2\sqrt{3}}{2}+3aH$.

Stąd otrzymujemy funkcję jednej zmiennej opisującą pole powierzchni naszego graniastosłupa w zależności od długości krawędzi podstawy

$P_c\left(a\right)=\frac{a^2\sqrt{3}}{2}+\frac{16\sqrt{3}}{a}$.

Zmienna $a$ musi być dodatnia więc

$D:a\in \left(0,\infty \right)$.

Wyznaczymy pochodną po zmiennej $a$.

$P_c^{\mathrm{\prime }}\left(a\right)=a\sqrt{3}-\frac{16\sqrt{3}}{a^2}$.

Wyznaczymy miejsce zerowej pochodnej $a^3\sqrt{3}=16\sqrt{3}$, stąd $a=2\sqrt[3]{2}$.

Aby wyznaczyć ekstremum, posłużymy się tabelą, przedziały w tabeli są zależne od dziedziny oraz punktów dla których pochodna się zeruje.

Funkcja osiąga minimum dla $a=2\sqrt[3]{2} \mathrm{cm}$, zatem pole powierzchni całkowitej graniastosłupa będzie najmniejsze z możliwych, gdy krawędź podstawy będzie miała długość $a=2\sqrt[3]{2} \mathrm{cm}$.

W stożek, w którym przekrojem osiowym jest trójkąt równoboczny o tworzącej długości $l$ wpisano walec o możliwie największym polu powierzchni całkowitej. Wyznaczymy długość promienia podstawy walca.

Rozwiązanie

Naszkicujemy przekrój osiowy stożka.

RqwrcTyUb348g

Ilustracja przedstawia przekrój osiowy stożka, który jest równoramiennym trójkątem A B C, gdzie podstawą jest A B, natomiast ramiona B C oraz C A  mają długość l. Z górnego wierzchołka C upuszczono wysokość do punktu E. Wewnątrz trójkąta rozrysowano prostokąt, którego dolna podstawa D F jest osadzona na podstawie A B. Nad punktem D będącym lewym dolnym wierzchołkiem prostokąta narysowano punkt G, górny lewy wierzchołek prostokąta. Punkt G należy do ramienia C A.

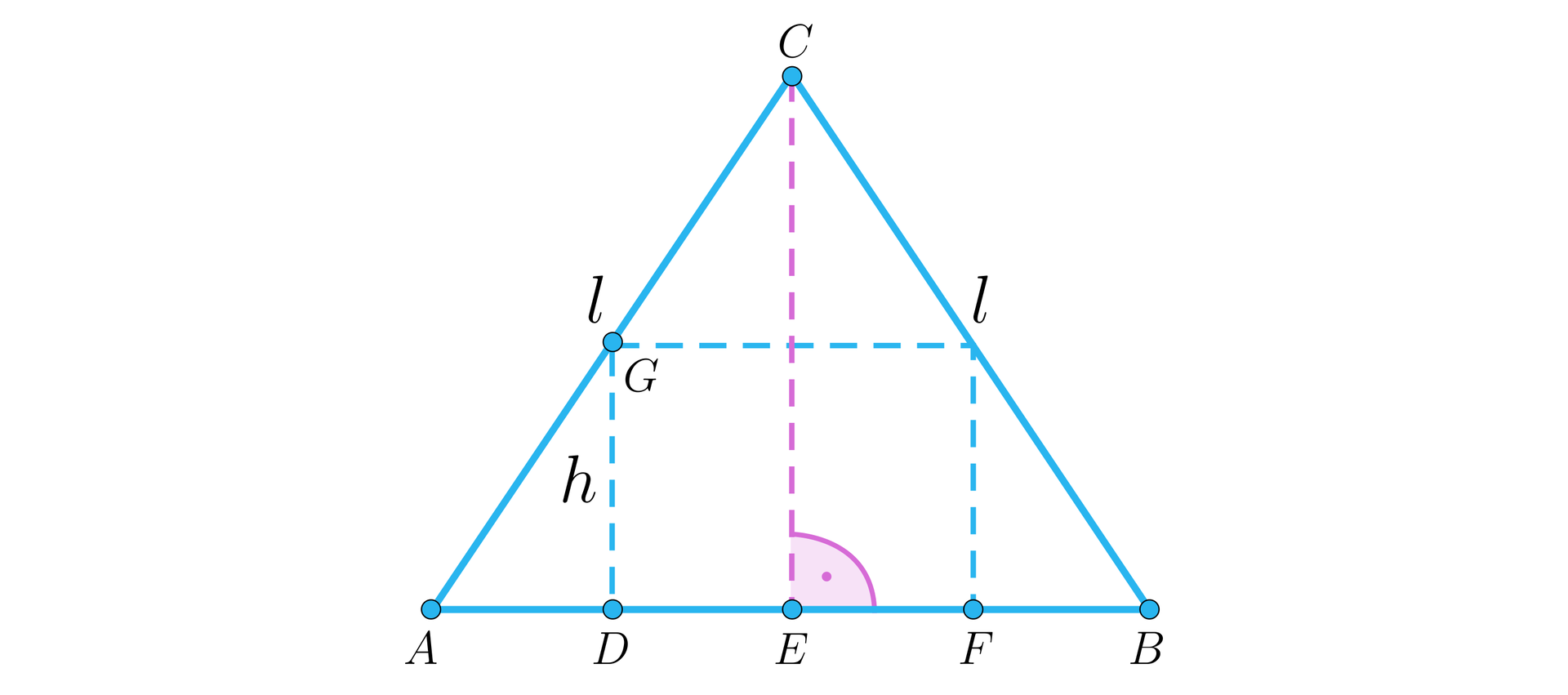
Oznaczmy:
$\left|AC\right|=\left|CB\right|=\left|AB\right|=l$,
$\left|CE\right|=H$ - wysokość stożka,
$\left|DE\right|=\left|EF\right|=r$ - promień podstawy walca.

Przekrojem osiowym stożka jest trójkąt równoboczny, więc $H=\frac{l\sqrt{3}}{2}$.

Z faktu, że $\left|AB\right|=l$ oraz $\left|DE\right|=r$, mamy

$\left|AD\right|=\left|FB\right|=\frac{l}{2}-r$.

Z podobieństwa trójkątów $AEC$ i $ADG$ otrzymujemy równość:

$\frac{H}{h}=\frac{\left|AE\right|}{\left|AD\right|}$.

Podstawiając oraz wyznaczając wysokość walca, otrzymujemy

$h=\sqrt{3}\left(\frac{l}{2}-r\right)$.

Wyznaczymy pole powierzchni całkowitej walca

$P_c=2\pi r\left(r+h\right)$.

Podstawiając otrzymujemy funkcję jednej zmiennej opisującą pole powierzchni całkowitej walca w zależności od długości promienia jego podstawy.

$P_c\left(r\right)=2\pi r\left(r+\sqrt{3}\left(\frac{l}{2}-r\right)\right)$.

Następnie wyznaczymy dziedzinę, oczywiście wszystkie zmienne muszą być dodatnie, więc $r>0$ oraz z wysokości walca $r<\frac{l}{2}$. Zatem

$D:x\in \left(0,\frac{l}{2}\right)$.

Wyznaczymy pochodną pola powierzchni całkowitej

$P_c^{\mathrm{\prime }}\left(r\right)=2\pi \left(r+\sqrt{3}\left(\frac{l}{2}-r\right)\right)+2\pi r\left(1-\sqrt{3}\right)$.

Wyznaczając miejsce zerowe pochodnej funkcji pola

$r=\frac{\left(\sqrt{3}-3\right)l}{8}$.

Aby wyznaczyć ekstremum, tworzymy tabelę, przedziały w tabeli są zależne od dziedziny oraz miejsc zerowych pochodnej.

Funkcja osiąga maksimum w punkcie $r=\frac{\left(\sqrt{3}-3\right)l}{8}$, zatem walec o możliwie największym polu powierzchni całkowitej ma promień podstawy $r=\frac{\left(\sqrt{3}-3\right)l}{8}$.

Objętość stożka wynosi $V\pi$. Wyznaczymy długości wysokości oraz promienia stożka, dla których pole powierzchni bocznej jest najmniejsze z możliwych.

Rozwiązanie

Naszkicujemy rzut stożka.

RXayRH4qdRWoE

Ilustracja przedstawia stożek o tworzącej l, o promieniu podstawy r oraz o wysokości H.

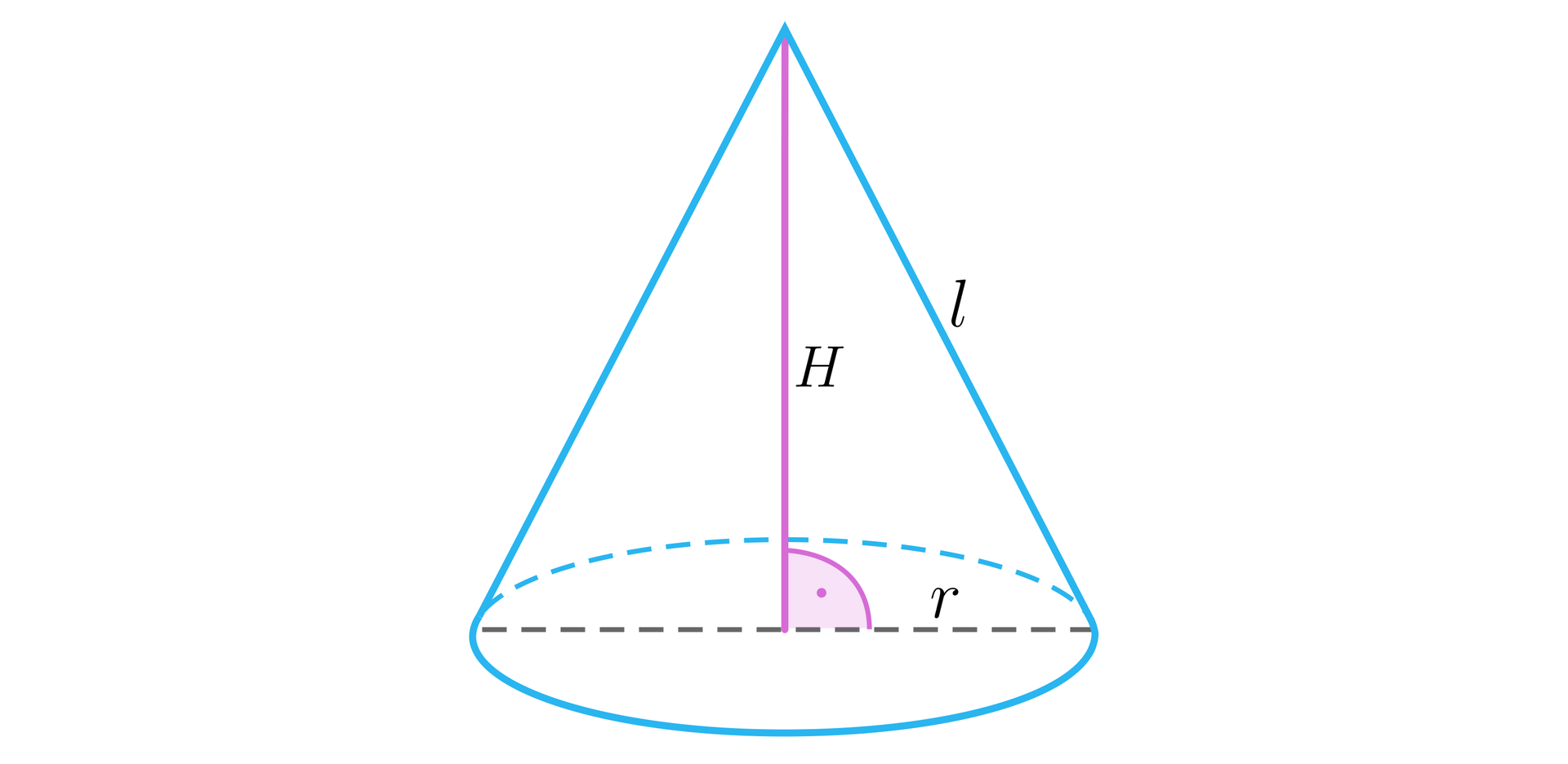
Rozpiszemy wzór na objętość

$V=\frac{1}{3}{P}_{p}H=\frac{1}{3}\pi r^{2}H$.

Wyznaczając promień oraz podstawiając objętość daną w treści zadania, otrzymujemy

$r=\sqrt{\frac{3V}{H}}$.

Z twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa

$l^2=r^2+H^2$.

Skąd po podstawieniu otrzymujemy

$l=\sqrt{H^2+\frac{3V}{H}}$.

Wyznaczymy pole powierzchni bocznej stożka

$P_b=\pi rl$.

Podstawiając wcześniej wyznaczone wielkości, otrzymujemy funkcje jednej zmiennej opisującą pole powierzchni bocznej stożka w zależności od jego wysokości

$P_b\left(H\right)=\pi \sqrt{\frac{3V}{H}}\sqrt{H^2+\frac{3V}{H}}=\sqrt{3VH{\pi }^2+\frac{9V^2{\pi }^2}{H^2}}$.

Wyznaczymy dziedzinę

$D:H\in \left(0,\infty \right)$.

Zauważmy, że funkcja $P_b\left(H\right)$ osiąga najmniejszą wartość wówczas, gdy wyrażenie pod pierwiastkiem osiąga najmniejszą wartość. Rozważmy

$f\left(H\right)=3VH{\pi }^2+\frac{9V^2{\pi }^2}{H^2}$.

Wyznaczymy pochodną

$f^{\mathrm{\prime }}\left(H\right)=3V{\pi }^2-\frac{18V^2{\pi }^2}{H^3}$.

Miejsce zerowe pochodnej wynosi $H=\sqrt[3]{6V}$.

Naszkicujemy wykres pochodnej.

R1F5QX7lUzMat

Ilustracja przedstawia poziomą oś H z zaznaczonym na niej punktem $\sqrt[3]{6V}$. Na rysunku znajduje się wykres funkcji w kształcie łuku. Wykres biegnie niemal pionowo spod osi do punktu $\sqrt[3]{6V}$, w którym przebija nad oś i zakręca w prawo, biegnąc niemal poziomo do plus nieskończoności. Wykres opisano jako $f\text{'}\left(H\right)$, a jego część nad osią oznaczono plusem, a pod osią minusem.

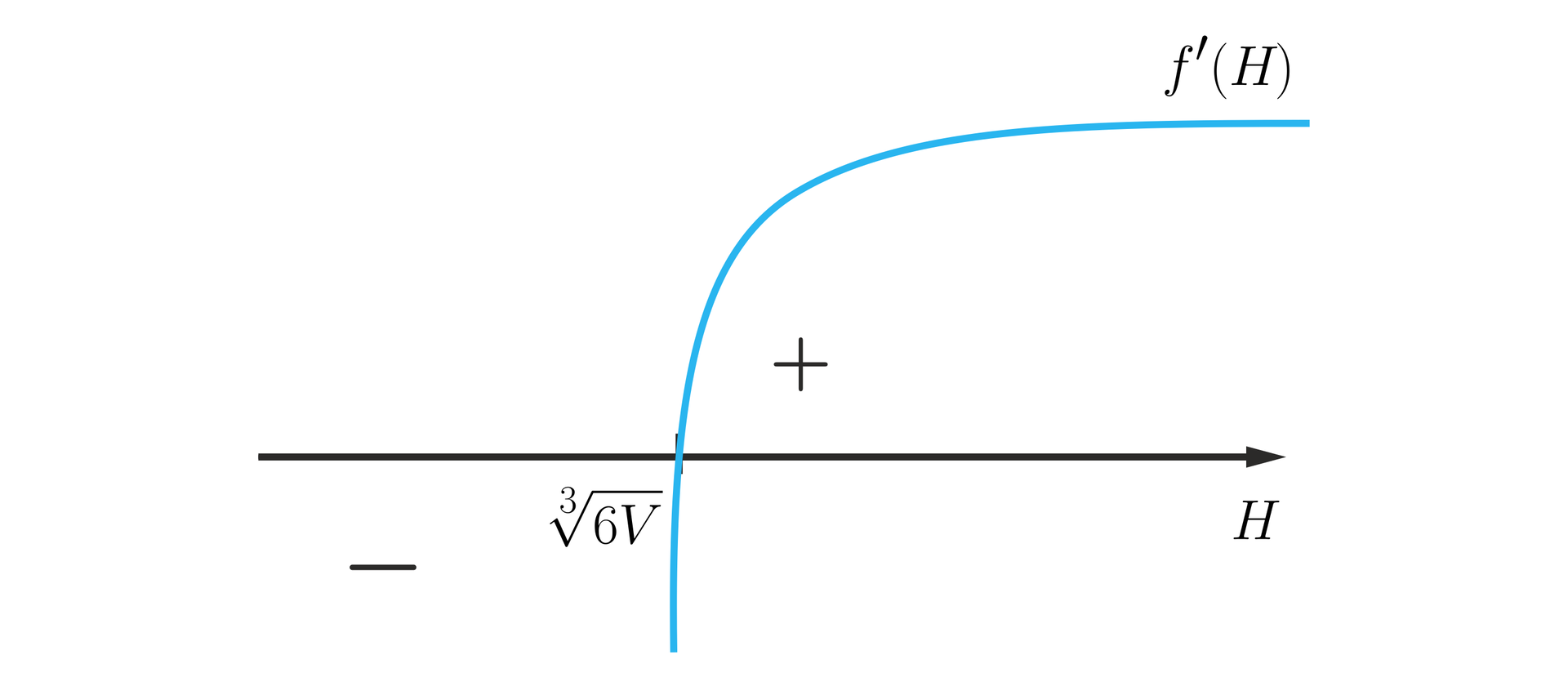
Aby wyznaczyć ekstremum, tworzymy tabelę, przedziały w tabeli są zależne od dziedziny oraz miejsc zerowych pochodnej.

Funkcja osiąga minimum w punkcie $H=\sqrt[3]{6}V$. Zatem pole powierzchni bocznej stożka będzie najmniejsze z możliwych, gdy $H=\sqrt[3]{6}V$ oraz $r=\frac{\sqrt[3]{3V}}{\sqrt[6]{2}}$.

Dany jest prostopadłościan o objętości $4$, w którym jedna krawędź podstawy jest dwa razy dłuższa od drugiej oraz suma długości krawędzi jest mniejsza od $38$. Wyznaczymy wymiary prostopadłościanu, którego pole powierzchni całkowite jest najmniejsze z możliwych.

Rozwiązanie

Oznaczmy

R1Pe3CXBo2PDL

Ilustracja przedstawia prostopadłościan o prostokątnej podstawie o wymiarach 2 x na x oraz o wysokości H.

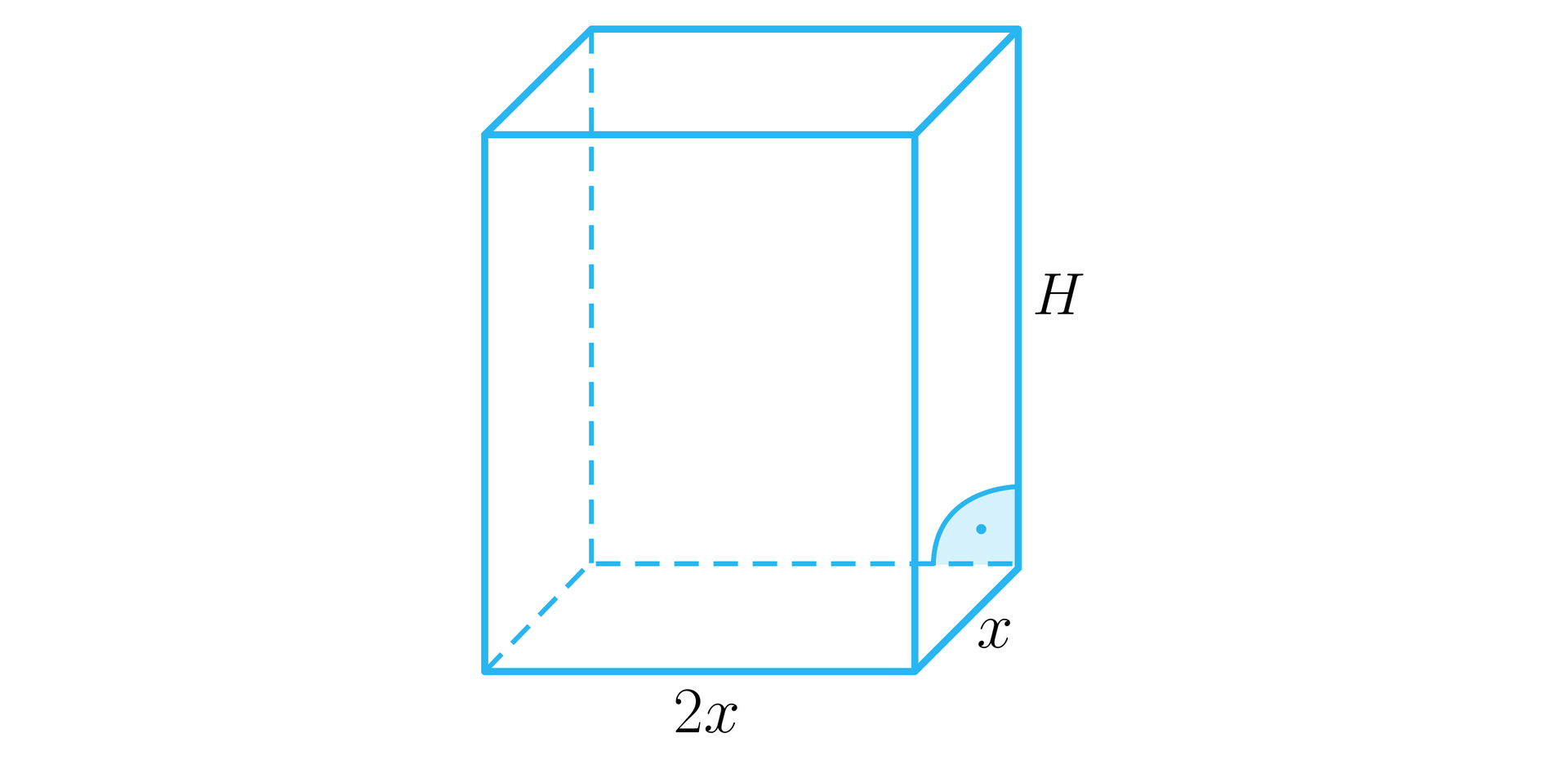
Ze wzoru na objętość $V=2x^{2}H$ oraz z sumy długości krawędzi $12x+4H<38$.

Wyznaczając wysokość, otrzymujemy $H=\frac{2}{x^2}$.

Podstawiając do nierówności oraz mnożąc obustronnie przez $x^2$, otrzymujemy $12x^3-38x^2+8<0$.

Możemy zauważyć, że miejscem zerowym powyższego wielomianu jest $\frac{1}{2}$. Wykonamy dzielenie wielomianów schematem Horneraschemat Horneraschematem Hornera.

Po dzieleniu otrzymujemy wielomian $12x^2-32x-16$.

Z trójmianu kwadratowego wyznaczymy miejsca zerowe, otrzymujemy $x_1=-\frac{2}{3}\sqrt{7}+\frac{4}{3}$ oraz $x_2=\frac{2}{3}\sqrt{7}+\frac{4}{3}$.

Ostatecznie otrzymaliśmy trzy miejsca zerowe wyjściowego wielomianu, naszkicujemy wykres.

R1Y0ULulQzIqm

Ilustracja przedstawia poziomą oś a z zaznaczonymi na niej czterema liczbami: x indeks dolny 1, 0, jedna druga, x indeks dolny dwa. Na rysunku przedstawiono sinusoidalny wykres wielomianu. Wykres biegnie następująco: od lewej narysowany jest linią przerywaną i biegnie pod osią od minus nieskończoności do x indeks dolny 1, gdzie przebija nad oś do niezamalowanego punktu oznaczonego nad zerem. Z tego punktu wykres biegnie w dół do punktu jedna druga. Stąd wykres jest narysowany linią ciągłą. W punkcie jedna druga przebija pod oś i wraca nad oś w punkcie x indeks dolny dwa. Części wykresu nad osią oznaczono plusami, a pod osią minusami.

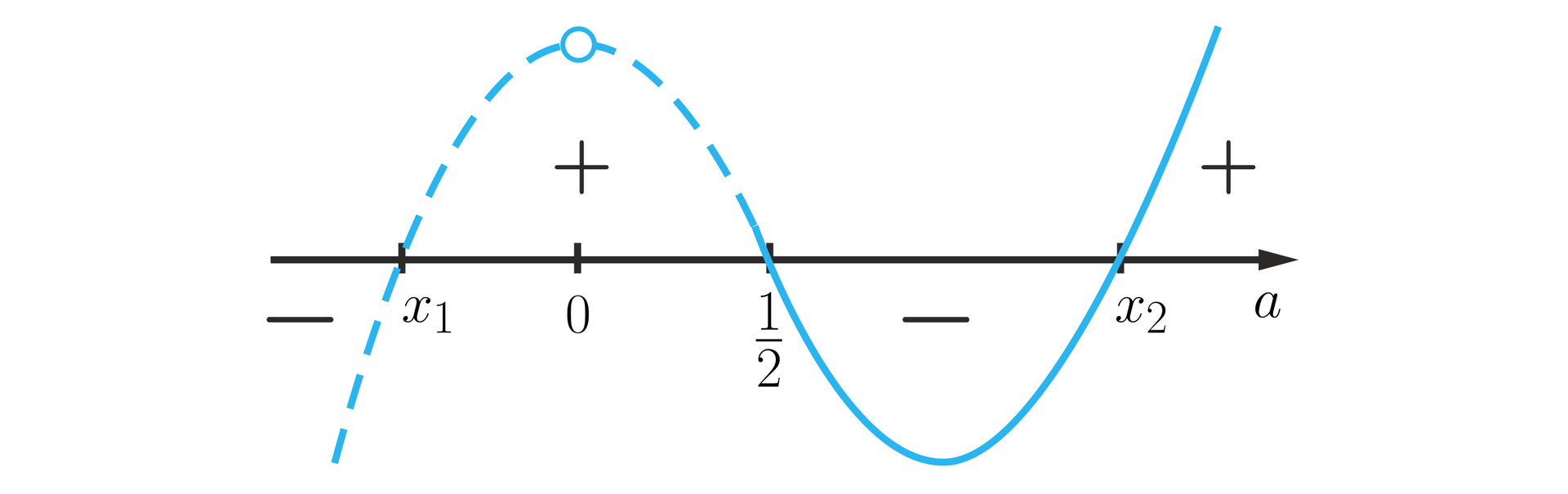
Zmienna $x$ jest krawędzią, więc musi być dodatnia oraz nierówność musi być mniejsza od zera więc z wykresu możemy odczytać dziedzinę

$D:x\in \left(\frac{1}{2},\frac{2}{3}\sqrt{7}+\frac{4}{3}\right)$.

Następnie wyznaczymy pole powierzchni całkowitej

$P_c=2P_p+P_b=4x^2+6xH$.

Podstawiając, otrzymujemy funkcję zmiennej $x$ opisującą pole powierzchni całkowitej prostopadłościanu w zależności od długości jednej z krawędzi podstawy.

$P_c\left(x\right)=4x^2+\frac{12}{x}$.

Wyznaczamy pochodną

$P_c^{\mathrm{\prime }}\left(x\right)=8x-\frac{12}{x^2}$.

Miejscem zerowym pochodnej jest $x=\sqrt[3]{1,5}$. Należy do dziedziny. Naszkicujemy wykres pochodnej.

R1JXT3jrgbLzn

Ilustracja przedstawia poziomą oś x z zaznaczonym na niej punktem $\sqrt[3]{1,5}$. Na rysunku znajduje się wykres w kształcie łuku, który biegnie od minus nieskończoności pod osią, przebija oś w punkcie $\sqrt[3]{1,5}$ i dalej rośnie, biegną w prawo. Część wykresu pod osią oznaczono minusem, a nad osią plusem.

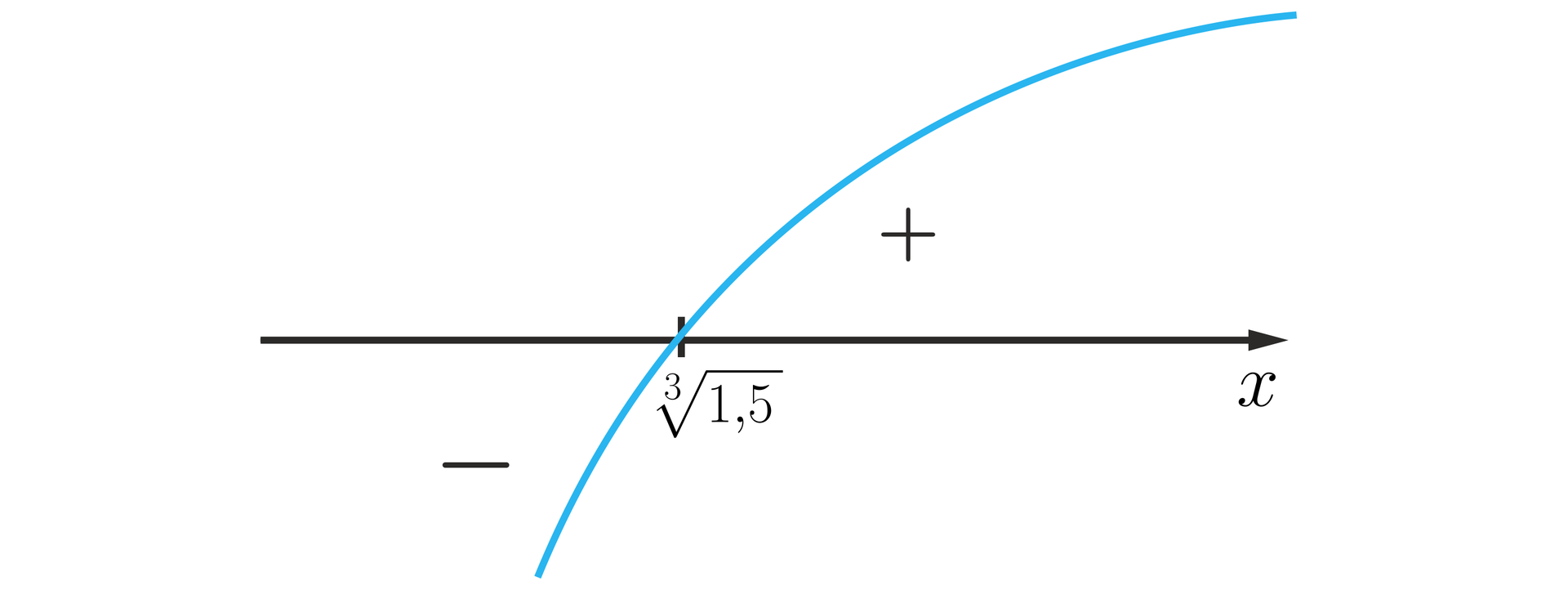
Aby wyznaczyć ekstremum, tworzymy tabelę, przedziały w tabeli są zależne od dziedziny oraz miejsc zerowych pochodnych

Funkcja osiąga minimum w punkcie $x=\sqrt[3]{1,5}$. Wyznaczymy $H=\frac{2}{\sqrt[3]{1,5^2}}$. Wymiary prostopadłościanu, którego pole powierzchni całkowite jest najmniejsze z możliwych, to $2\sqrt[3]{1,5}\times \sqrt[3]{1,5}\times \frac{2}{\sqrt[3]{1,5^2}}$.

gdy trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej

algorytm dzielenia wielomianu $w\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0$ przez dwumian postaci $x-a$. Dzielenie wykonuje się tworząc tabelkę. W pierwszym wierszu tabeli wpisujemy współczynniki wielomianu, w drugim wierszu wykonujemy działania. W dolnym wierszu w pierwszej komórce wpisuje się miejsce zerowe dwumianu. W drugiej komórce przepisuje się współczynnik przy najwyższej potędze wielomianu, a następnie wyniki obliczeń