Przeczytaj
WielościanWielościan foremny o ścianach w kształcie przystających trójkątów równobocznych. Ośmiościan foremny posiada krawędzi, wierzchołków i przekątne.
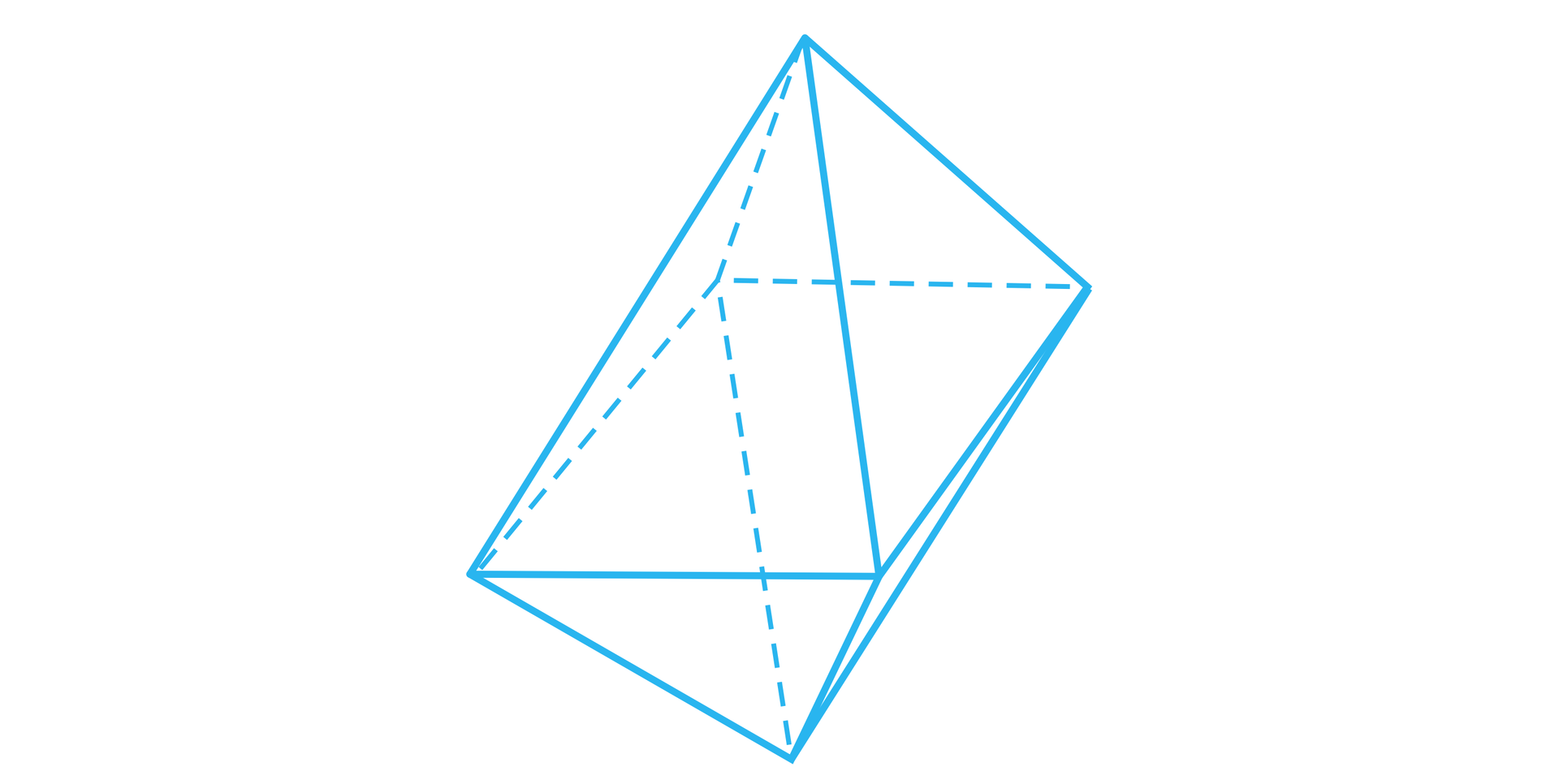
Otwórz aplet, zobacz jak wygląda ośmiościan i jego siatka.
Zapoznaj się z opisem apletu. Wyobraź sobie jak wygląda ośmiościan i jego siatka.
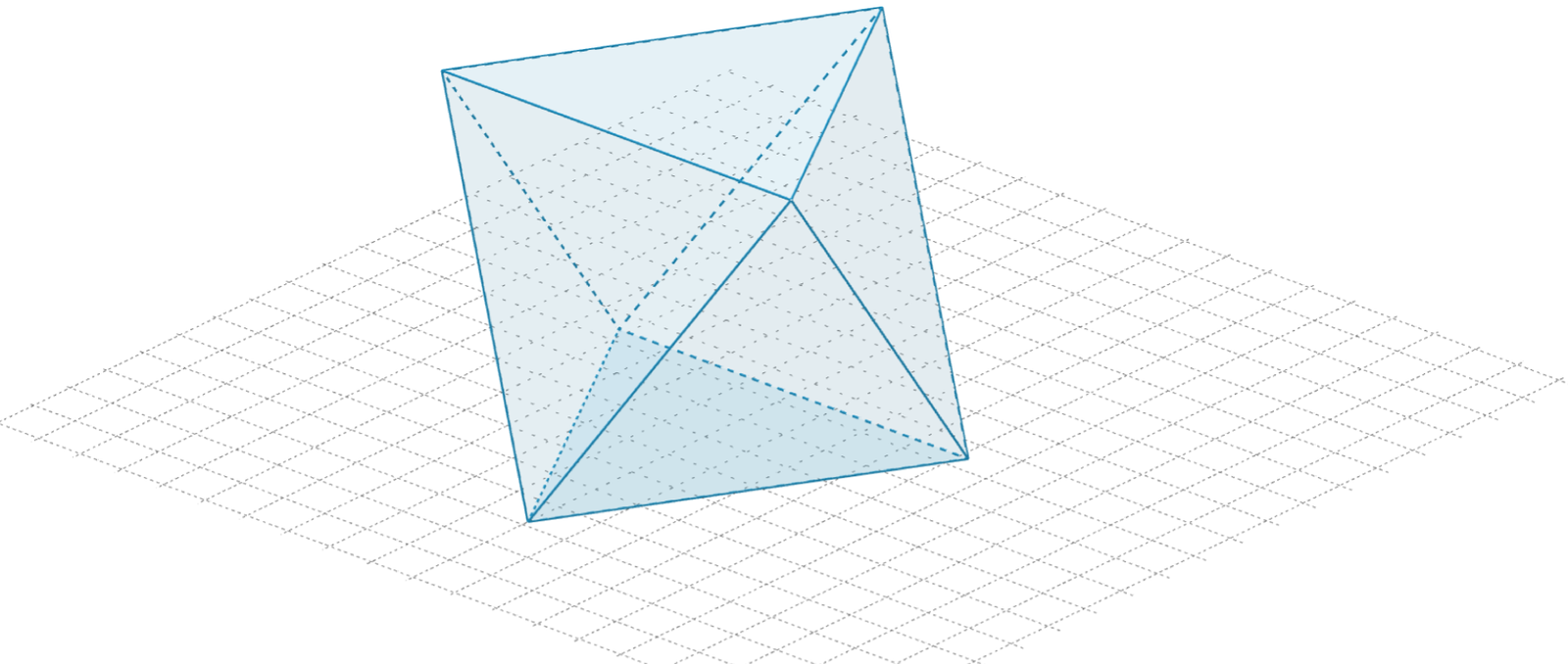
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DSd4h6qaI
Narysujemy taki przekrój ośmiościanu foremnego, który jest:
trójkątem równobocznym,
kwadratem,
rombem,
trapezem równoramiennym.
Rozwiązanie
Trójkąt równoboczny otrzymamy, gdy płaszczyzna przejdzie przez wierzchołki dowolnej ściany. Jest to szczególny przypadek przekroju, dlatego trójkąt równoboczny będziemy raczej traktować jako ścianę ośmiościanu.
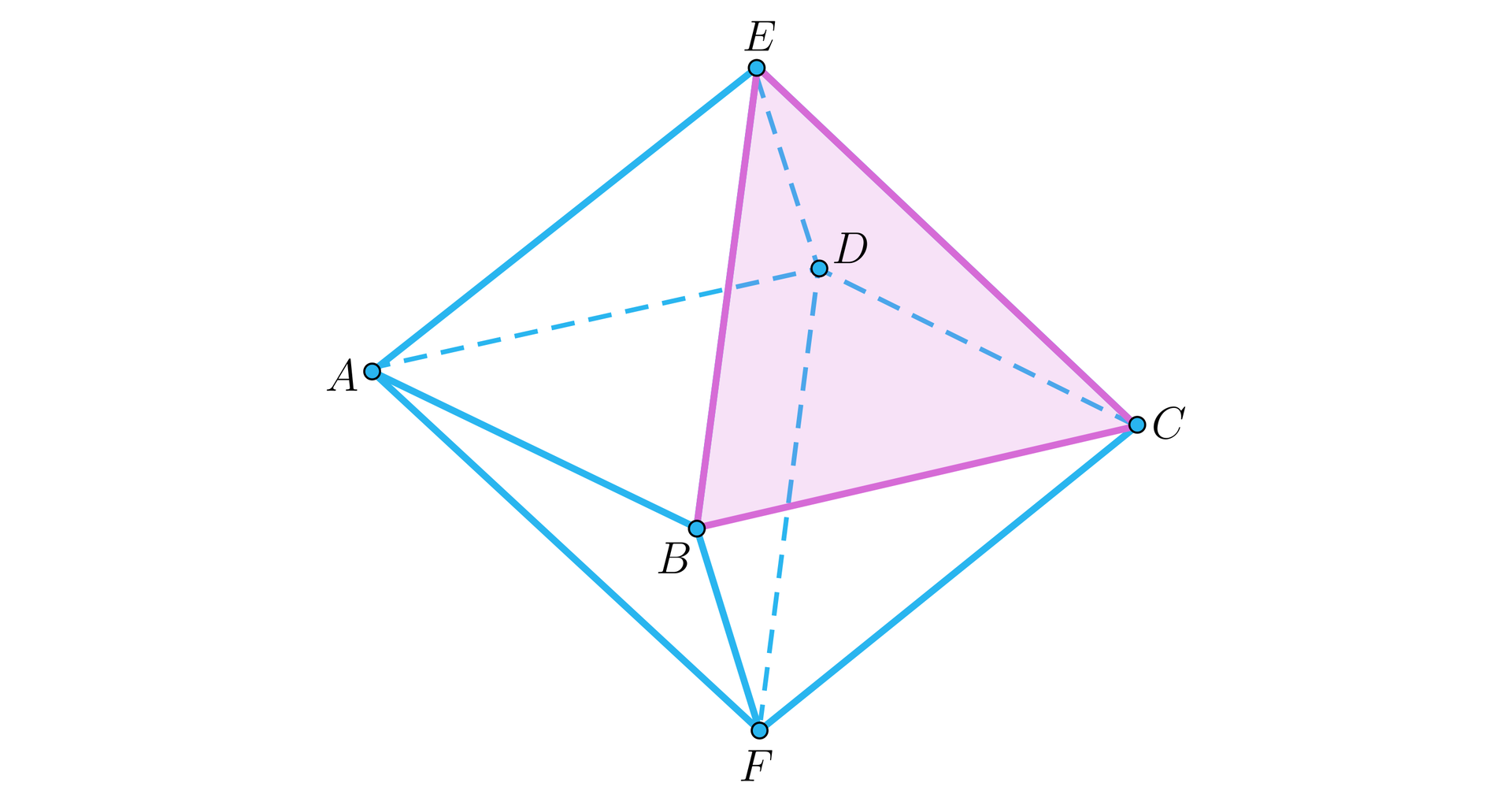
Jeśli płaszczyznę poprowadzimy, na przykład, przez wierzchołki , , , lub równolegle do takiej płaszczyzny, w przekroju otrzymamy kwadrat.
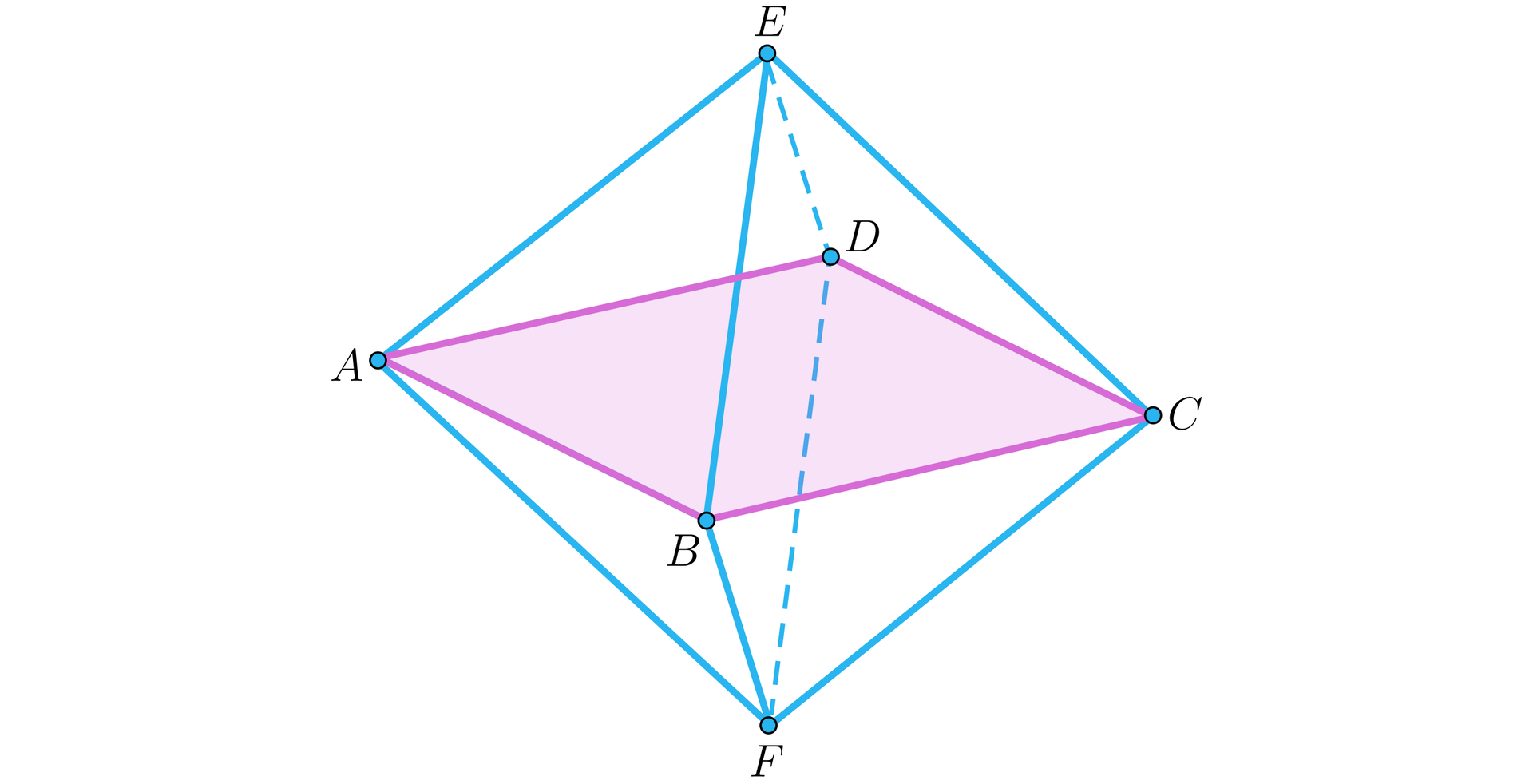
Przekrój będzie miał kształt rombu, gdy płaszczyzna przejdzie przez dwa przeciwległe wierzchołki ośmiościanu, na przykład i .
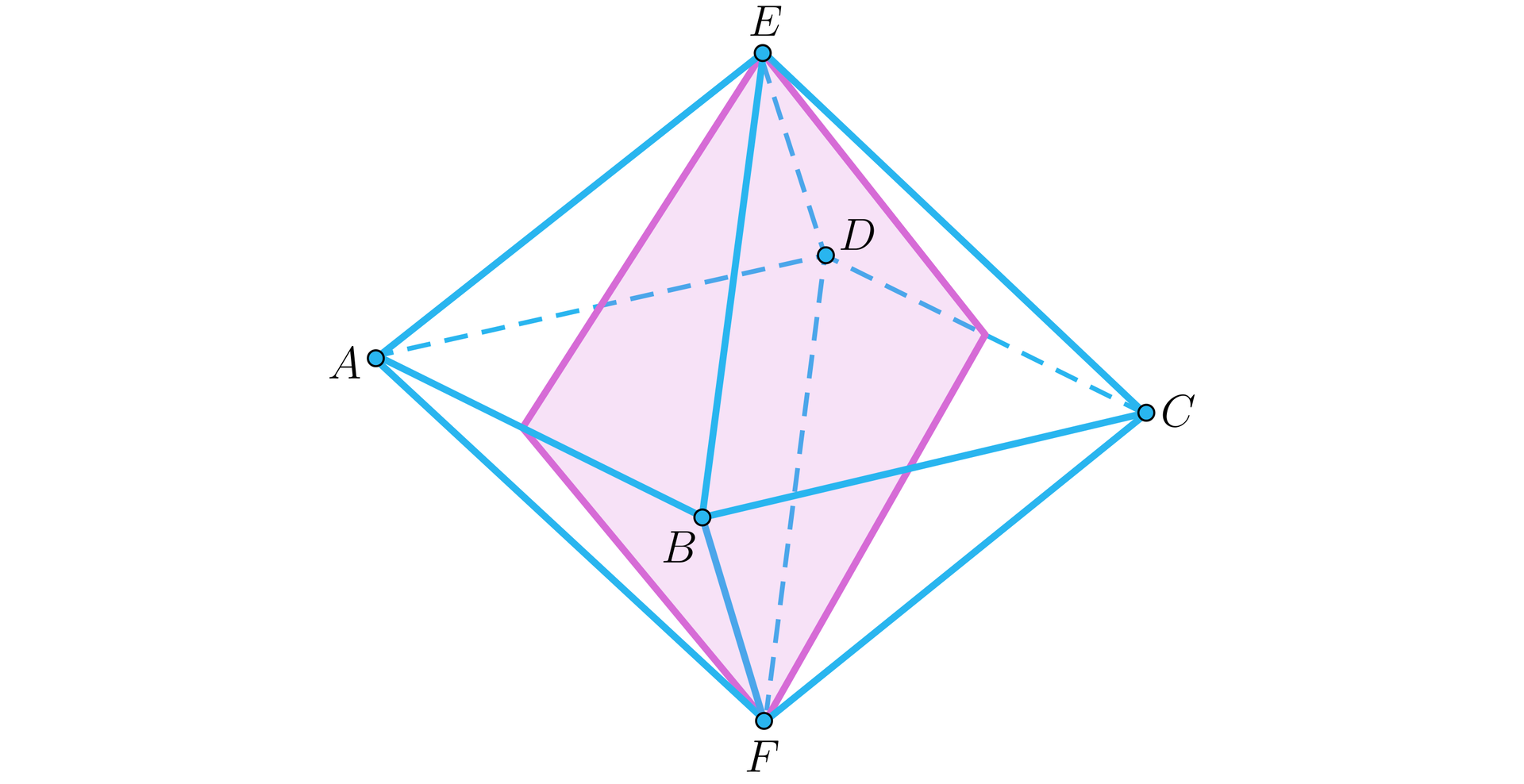
Trapez równoramienny otrzymamy, gdy płaszczyzna przejdzie przez wierzchołki i oraz przetnie krawędzie i .
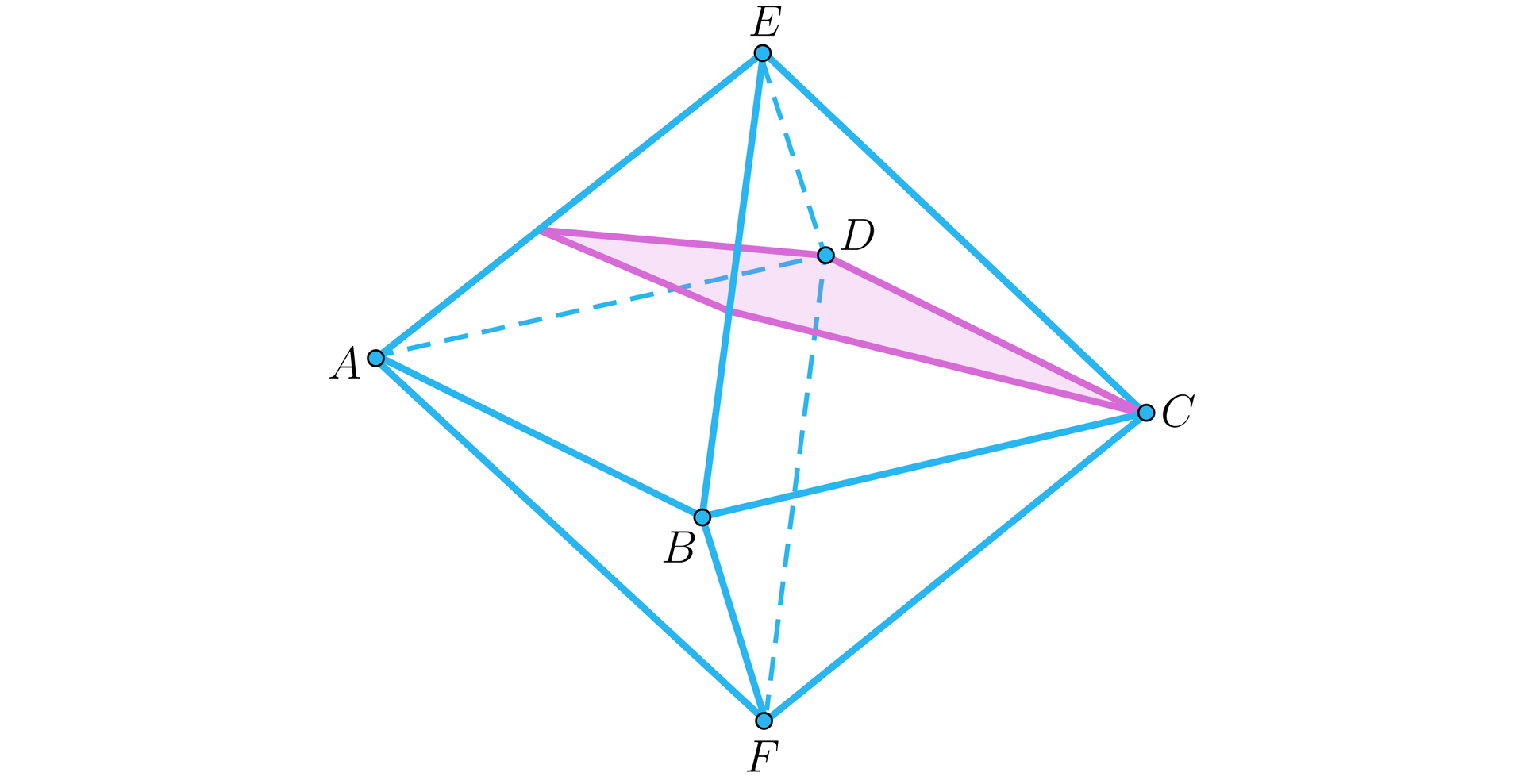
Ośmiościan o krawędzi przecięto płaszczyzną równoległą do płaszczyzn trójkątów i oraz przechodzącą przez środki pozostałych krawędzi. Obliczymy pole otrzymanego w ten sposób przekroju.
Rozwiązanie
Zacznijmy od narysowania rysunku:
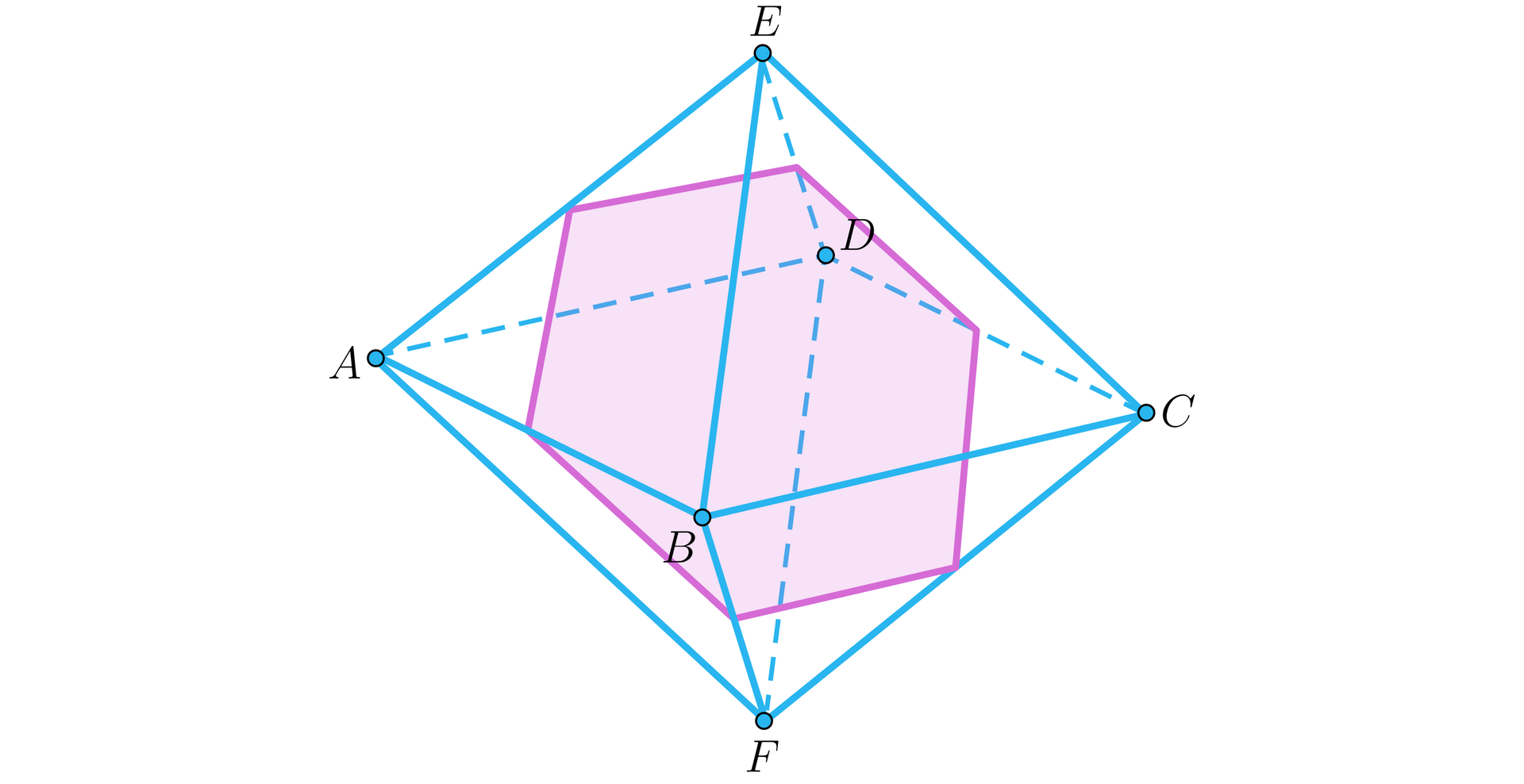
Zauważmy, że przekrój jest sześciokątem foremnym. Długość boku przekroju jest połową długości krawędzi ośmiościanu. Zatem pole przekroju wynosi:
.
Przekrój ośmiościanu foremnego płaszczyzną, która przechodzi przez jego dwa przeciwległe wierzchołki oraz środki dwóch przeciwległych krawędzi jest rombem o polu równym . Obliczymy sumę długości wszystkich krawędzi tego ośmiościanu.
Rozwiązanie
Wykonajmy rysunek pomocniczy:
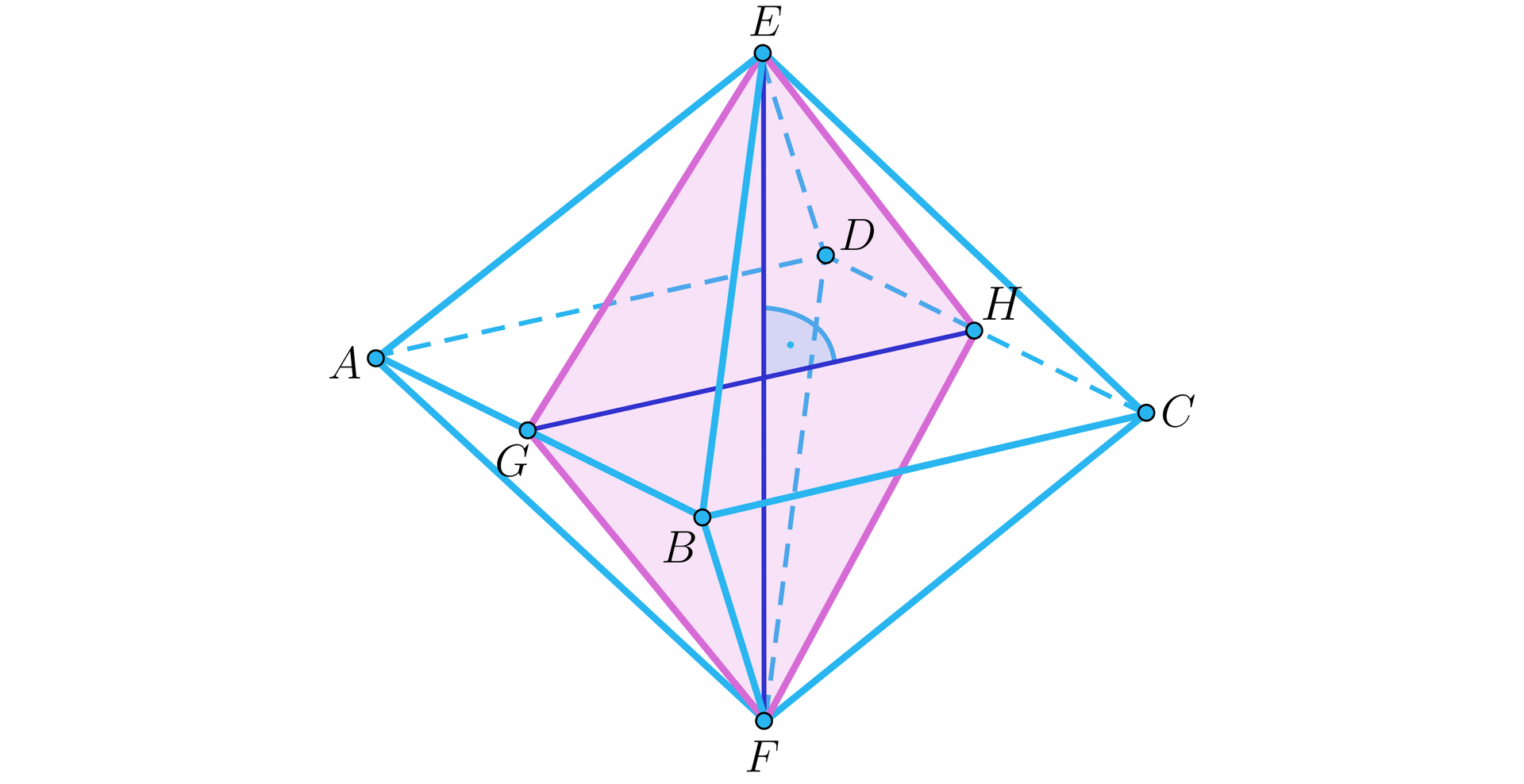
Oznaczmy jako długość krawędzi ośmiościanu. Wówczas . Bok rombu jest wysokością trójkąta równobocznego , więc . Oznaczmy drugą przekątną rombu jako . Ze wzoru na pole rombu mamy:
.
Przekątne rombu podzieliły go na trójkąty prostokątne, zatem zgodnie z twierdzeniem Pitagorasa mamy:
.
Zatem suma długości krawędzi ośmiościanu wynosi:
.
Wzory na promień kuli wpisanej w ośmiościan oraz promień kuli opisanej na ośmiościanie:
promień kuli wpisanej w ośmiościan:
promień kuli opisanej na ośmiościanie:
W ośmiościan wpisano kulę o promieniu . Obliczymy, ile razy większa jest objętość kuli opisanej na wielościanie od objętości kuli wpisanej w ośmiościan.
Rozwiązanie
Wiadomo, że promień kuli wpisanej w ośmiościan o krawędzi długości wyraża się wzorem .
Obliczymy :
.
Zatem promień kuli opisanej na ośmiościanie ma długość:
.
Obliczymy objętości naszych kul:
,
,
.
Objętość kuli opisanej na wielościanie jest razy większa od objętości kuli wpisanej.
Pole powierzchni kuli opisanej na ośmiościanie wynosi . Obliczmy sumę długości krawędzi naszego ośmiościanu.
Rozwiązanie
Niech - długość promienia okręgu opisanego na ośmiościanie, - długość krawędzi ośmiościanu.
Wówczas mamy .
Ponadto:
.
Obliczmy długość krawędzi wielościanu:
.
Zatem suma długości krawędzi ośmiościanu wynosi:
.
Wyznacz sumę długości krawędzi ośmiościanu, jeśli jego przekrojem jest trapez równoramienny o polu równym , w którym stosunek długości podstaw wynosi oraz wiadomo, że dłuższa podstawa pokrywa się z krawędzią ośmiościanu.
Rozwiązanie
Z treści zadania wiadomo, że przekrojem ośmiościanu jest trapez równoramienny, w którym stosunek długości podstaw wynosi oraz dłuższa podstawa tego trapezu jest krawędzią ośmiościanu, zatem krótsza podstawa to odcinek łączący środki dwóch krawędzi przeciwległej ściany. Oznaczmy długość krawędzi ośmiościanu przez a długość ramienia przekroju przez .
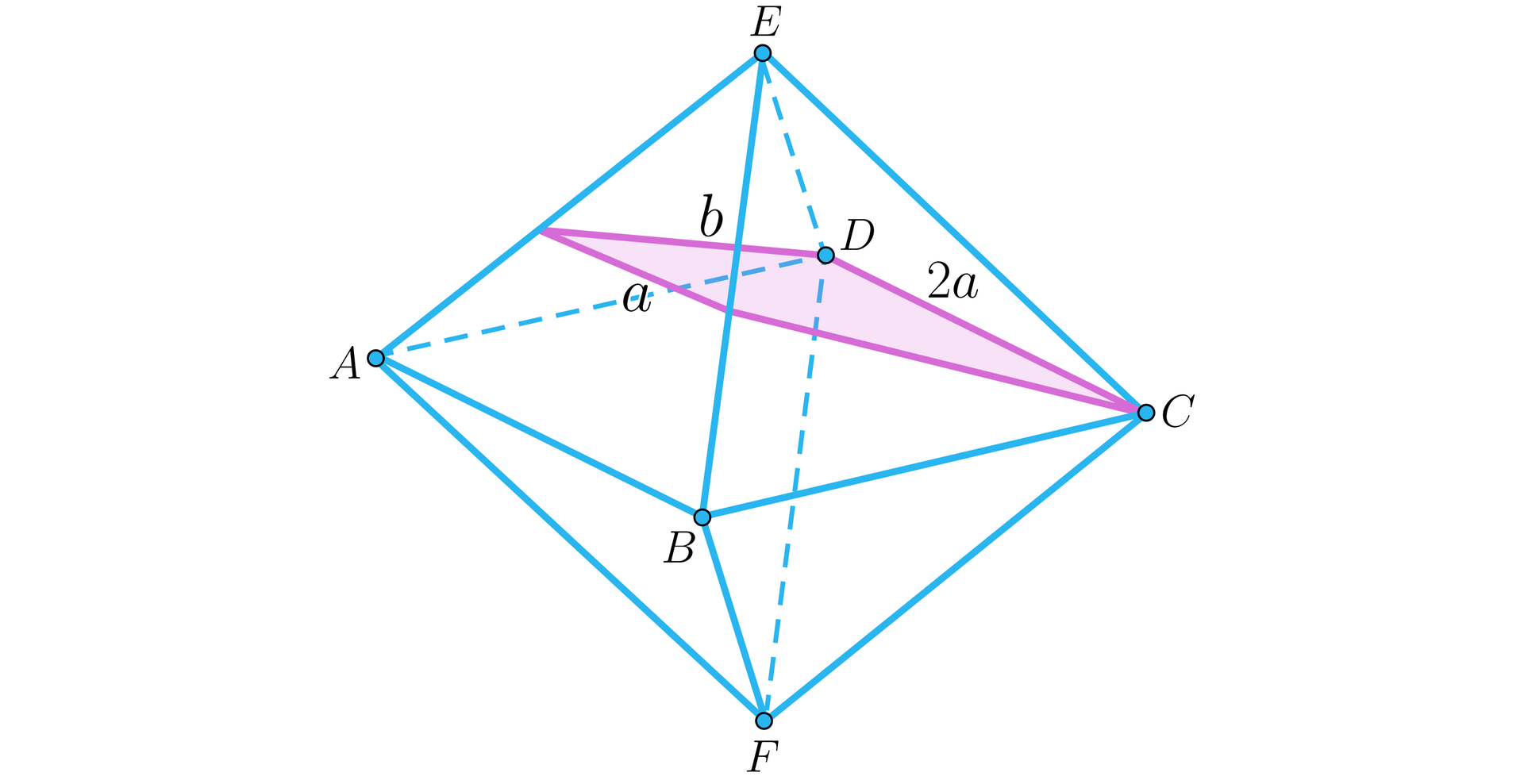
Zauważmy, że ramię tego trapezu łączy wierzchołek trójkąta równobocznego ze środkiem przeciwległego boku, zatem .
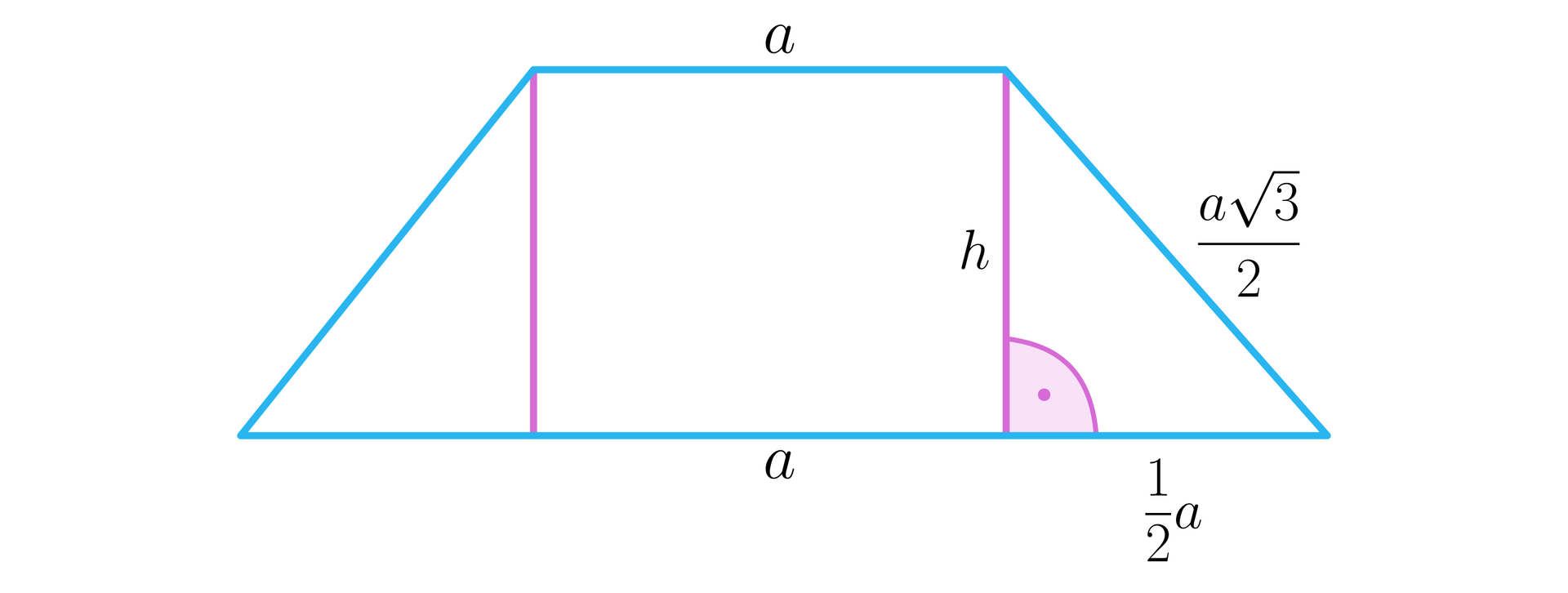
Z twierdzenia Pitagorasa wyznaczmy długość wysokości trapezu: . Zatem: co daje: , stąd: . Krawędź ośmiościanu ma więc długość , a suma długości wszystkich krawędzi wynosi: .
Ścinając wierzchołki ośmiościanu foremnego, otrzymujemy wielościan półforemny nazywany ośmiościanem ściętym. Wielościany półforemne nazywane są bryłami archimedesowymi, w przeciwieństwie do wielościanów foremnych, które znane są jako bryły platońskie.
Uruchom aplet i sprawdź, z jakich figur zbudowane są ściany ośmiościanu ściętego. Dlaczego bryła ta jest wielościanem półforemnym?
Zapoznaj się z opisem apletu i odpowiedz na pytania. Z jakich figur zbudowane są ściany ośmiościanu ściętego? Dlaczego bryła ta jest wielościanem półforemnym?
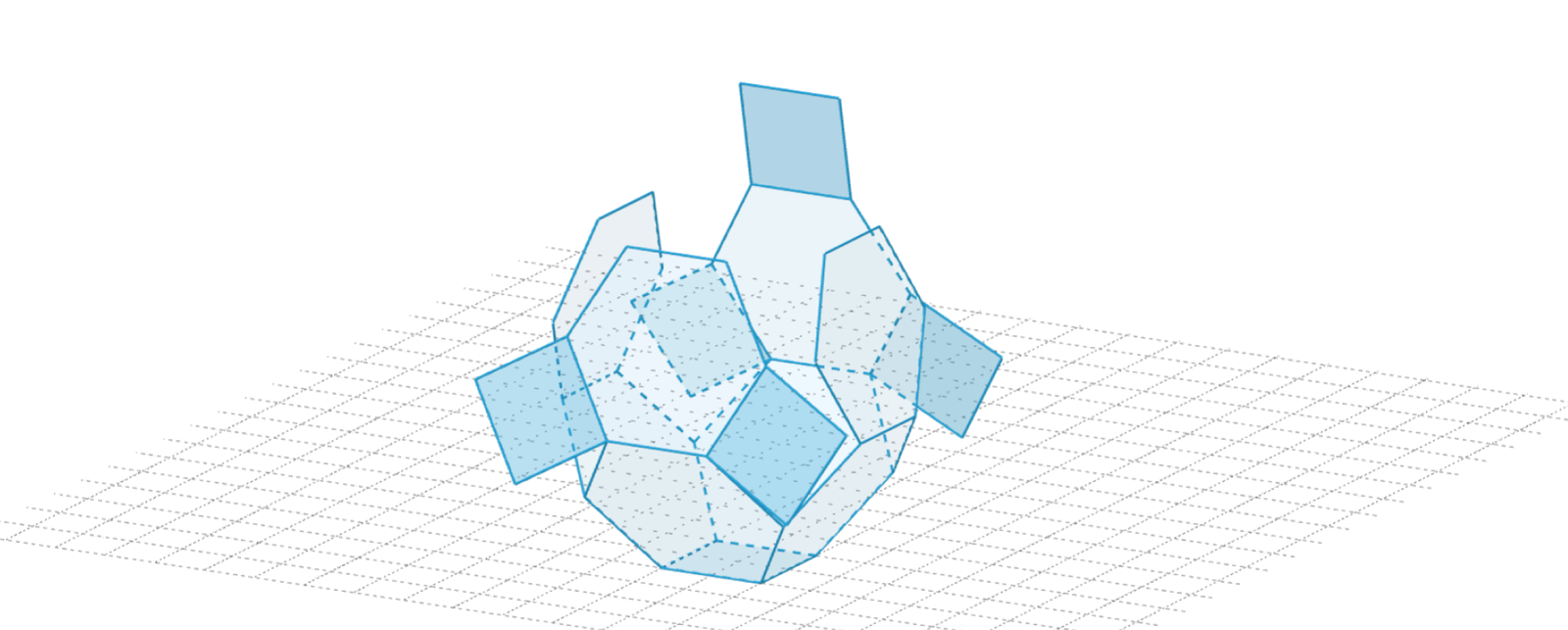
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DSd4h6qaI
OdpowiedźOdpowiedź
Słownik
bryła geometryczna, ograniczona przez tak zwaną powierzchnię wielościenną, czyli powierzchnię utworzoną z wielokątów o rozłącznych wnętrzach i każdym boku wspólnym dla dwóch wielokątów; każdy wielościan utworzony jest ze ścian – wielokątów, które razem tworzą powierzchnię wielościanu
Źródło: www.wikipedia.pl