Rozważmy funkcję $f$ określoną w pewnym otoczeniu $U$ punktu $x_0$. Wówczas funkcja $f$ ma w punkcie $x_0$:

• maksimum lokalne wtedy i tylko wtedy, gdy istnieje takie otoczenie $U$ punktu $x_0$, że dla każdego $x\in U \cap D_f$ spełniona jest nierówność $f\left(x\right)\leq f\left(x_0\right)$,

• minimum lokalne wtedy i tylko wtedy, gdy istnieje takie otoczenie $U$ punktu
  $x_0$, że dla każdego $x\in U \cap D_f$ spełniona jest nierówność $f\left(x\right)\geq f\left(x_0\right)$.

Funkcja różniczkowalna $f$ może mieć ekstremum jedynie w punktach, w których jej pochodna jest równa zeru.

Jeżeli funkcja $f$ jest ciągła w punkcie $x_0 \in D_f$ i ma pochodną w pewnym sąsiedztwie $S\left(x_0,\delta\right)$, wówczas:

1. jeśli $f'\left(x\right)$ $>$ $0$ dla $x \in \left(x_0-\delta,x_0\right)$ i $f'\left(x\right)$ $<$ $0$ dla $x \in \left(x_0,x_0+\delta\right)$, to funkcja ma w punkcie $x_0$ maksimum lokalne (zmiana znaku pierwszej pochodnej przy przejściu przez punkt $x_0$ z dodatniego na ujemny),

2. jeśli $f'\left(x\right)$ $<$ $0$ dla $x \in \left(x_0-\delta,x_0\right)$ i $f'\left(x\right)$ $>$ $0$ dla $x \in \left(x_0,x_0+\delta\right)$, to funkcja ma w punkcie $x_0$ minimum lokalne (zmiana znaku pierwszej pochodnej przy przejściu przez punkt $x_0$ z ujemnego na dodatni).

Na prostokącie $ABCD$ opisano okrąg o promieniu $r$. Wyznaczymy możliwie największe pole tego prostokąta.

Rozwiązanie

Oznaczmy

R1UPZBuGuziLl

Rysunek przedstawia okrąg o promieniu r i wpisany w niego prostokąt, o bokach a i b.

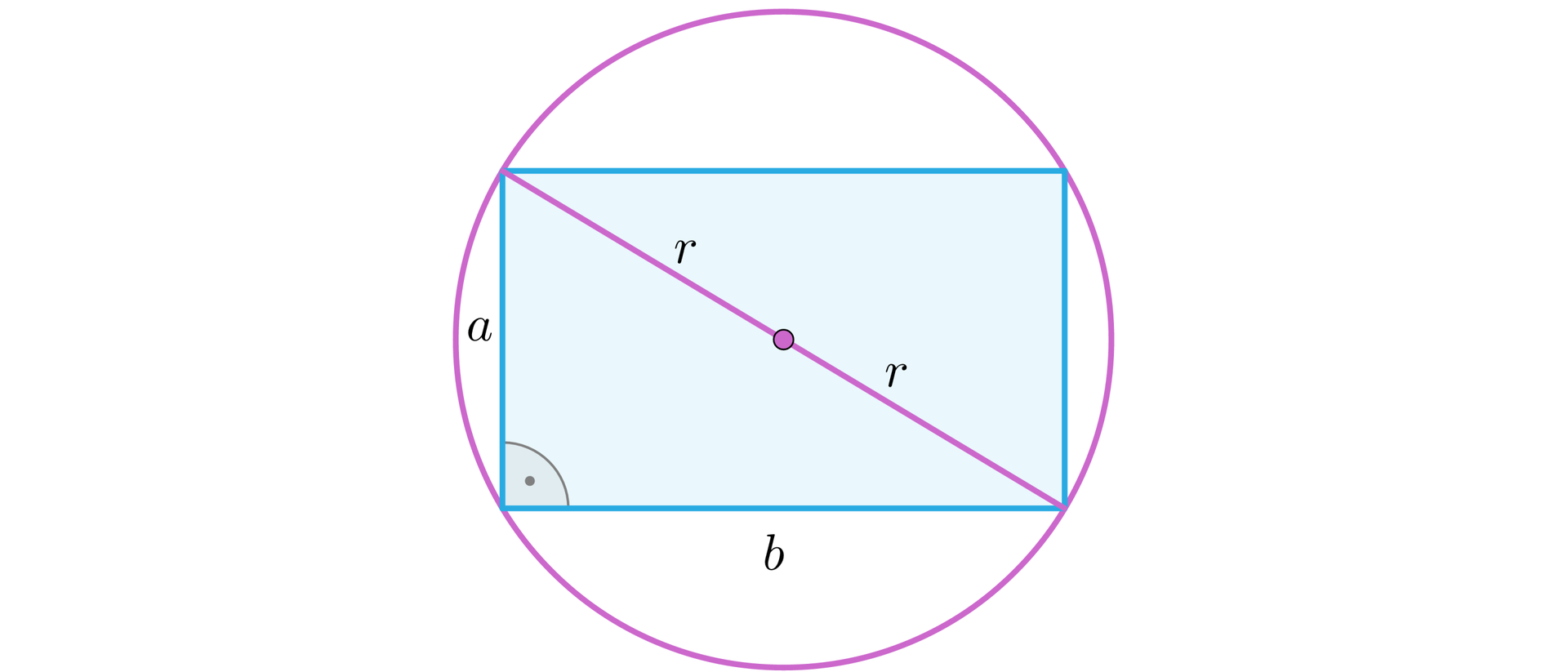
Długości boków prostokąta $a$ i $b$ muszą być liczbami dodatnimi oraz mniejszymi od $2r$. Korzystamy z twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa

$a^2+b^2=\left(2r\right)^2$

Zatem $b=\sqrt{4r^2-a^2}$, a pole prostokąta wynosi:

$P\left(a\right)=a\cdot\sqrt{4r^2-a^2}=\sqrt{a^2\left(4r^2-a^2\right)}=\sqrt{4r^2a^2-a^4}$

Dziedziną tej funkcji jest zbiór: $D_f$ : $a\in\left(0,2r\right)$.

Aby funkcja $P$ osiągała największą wartość wystarczy, by wyrażenie pod pierwiastkiem się zmaksymalizowało. Rozważmy funkcję: $f\left(a\right)=4r^2a^2-a^4$.

Wyznaczamy pochodną funkcji $f$:

$f'\left(a\right)=8r^2a-4a^3=4a\left(2r^2-a^2\right)=4a\left(r\sqrt{2}-a\right)\left(r\sqrt{2}+a\right)$.

Wyznaczamy ekstrema lokalne funkcji $f$, korzystając z warunku koniecznego (pochodną funkcji $f$ przyrównujemy do zera). Zauważmy, że istnieją trzy miejsca zerowe wielomianu $w\left(a\right)=4a\left(2r^2-a^2\right)=4a\left(r\sqrt{2}-a\right)\left(r\sqrt{2}+a\right)$.

Są to $a_1=-r\sqrt{2}$, $a_2=0$, $a_3=r\sqrt{2}$. Naszkicujemy wykres wielomianu $w$, funkcja $f'$ pokrywa się z nim w swojej dziedzinie.

RqG3K7kLFVxM1

Rysunek przedstawia wykres funkcji f od prim, oznaczono miejsca zerowe. W minus r pierwiastków z dwóch funkcja zmienia wartości dodanie w ujemne. W zerze funkcja zmienia wartości ujemne na dodatnie. W r pierwiastków z dwóch funkcja zmienia wartości dodatnie w ujemne.

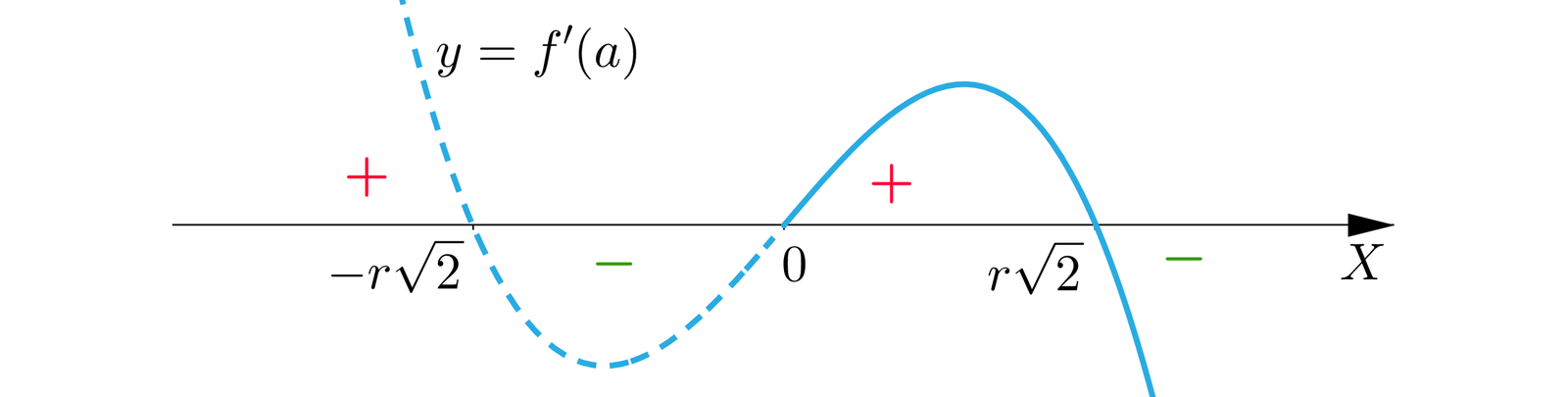
Aby wyznaczyć ekstremum, tworzymy tabelę:

Funkcja $f$ osiąga maksimum dla  $a=r\sqrt{2}$. Obliczymy największe pole.

$P\left(r\sqrt{2}\right)=r\sqrt{2}\cdot\sqrt{4r^2-\left(r\sqrt{2}\right)^2}=r\sqrt{2}\cdot r\sqrt{2}=2r^2$

Parabola o równaniu $y=3-\frac{1}{3}x^2$ przecina oś $X$ układu współrzędnych w punktach $A\left(-3,0\right)$ i $B\left(3,0\right)$. Rozpatrujemy wszystkie trapezy równoramienne $ABCD$, których dłuższą podstawą jest odcinek $AB$, zaś wierzchołki $C$ i $D$ leżą na paraboli (zobacz rysunek). Wyznaczymy pole trapezu $ABCD$ w zależności od pierwszej współrzędnej wierzchołka $C$. Obliczymy współrzędne wierzchołka $C$ tego trapezu, którego pole jest największe.

R1IAHamsoe17s

Ilustracja przedstawia układ kartezjańskim na którym zaznaczono funkcję y i trapez A, B, C, D równoramienny. Wierzchołki trapezu zawierają się w funkcji y.

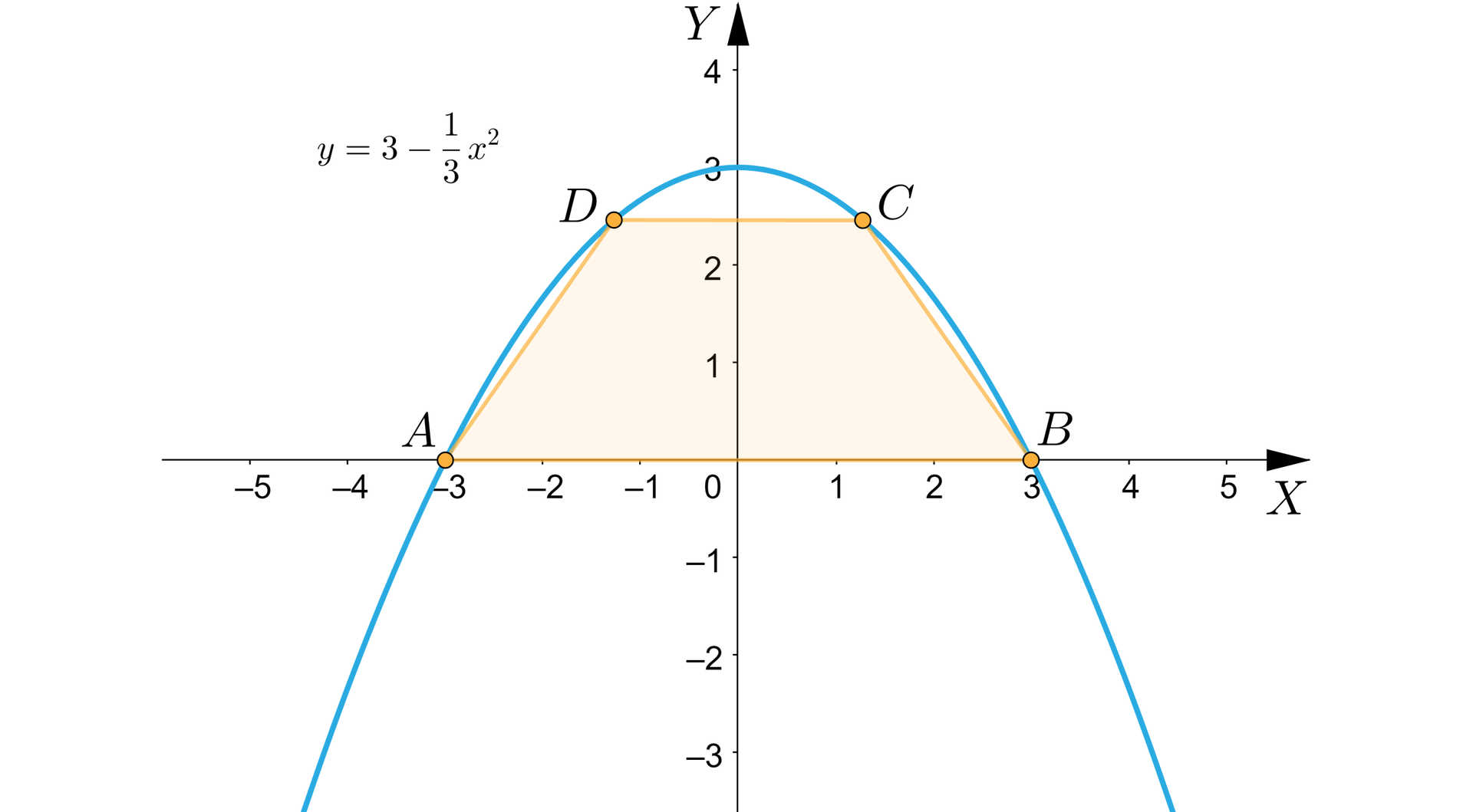
Rozwiązanie

Ponieważ punkt $C$ leży na paraboli o równaniu $y=3-\frac{1}{3}x^2$, to: $C\left(x,3-\frac{1}{3}x^2\right)$. Możemy zauważyć, że druga współrzędna wierzchołka $C$ oznacza długość wysokości trapezu.

Mamy zatem $h=3-\frac{1}{3}x^2$, $\left|AB\right|=6$ oraz $\left|CD\right|=2x$.

Podstawmy dane do wzoru na pole trapezu:

$P\left(x\right)=\frac{2x+6}{2}\left(3-\frac{1}{3}x^2\right)=\frac{1}{3}\left(x+3\right)\left(9-x^2\right)=\frac{1}{3}\left(-x^3-3x^2+9x+27\right)$.

Wyznaczymy dziedzinę tej funkcji. Wierzchołek $C$ znajduje się na prawo od osi $Y$ a jego pierwsza współrzędna jest liczbą mniejszą niż $3$, więc $D$ : $x \in \left(0,3\right)$.

Wyznaczymy pochodną funkcji $P$:

$P'\left(x\right)=\frac{1}{3}\left(-3x^2-3\cdot 2 x+9\right)=\frac{1}{3}\left(-3x^2-6x+9\right)$.

Wyznaczymy ekstrema lokalne funkcji $P$: $P'\left(x\right)=0$,

wtedy i tylko wtedy, gdy $\frac{1}{3}\left(-3x^2-6x+9\right)=0$

Obliczając miejsca zerowe trójmianu kwadratowego otrzymujemy $x_1=1$ i $x_2=-3$. Zauważmy, że $x_1=1 \in D$ i $x_2=-3\notin D$. Naszkicujemy wykres pochodnej (interesuje nas fragment zgodny z dziedziną).

RKNCkIzAMCU0r

Rysunek przedstawia wykres funkcji P prim, który jest parabolom o ramionach skierowanych w dół i miejscach zerowych w minus trzy i jeden.

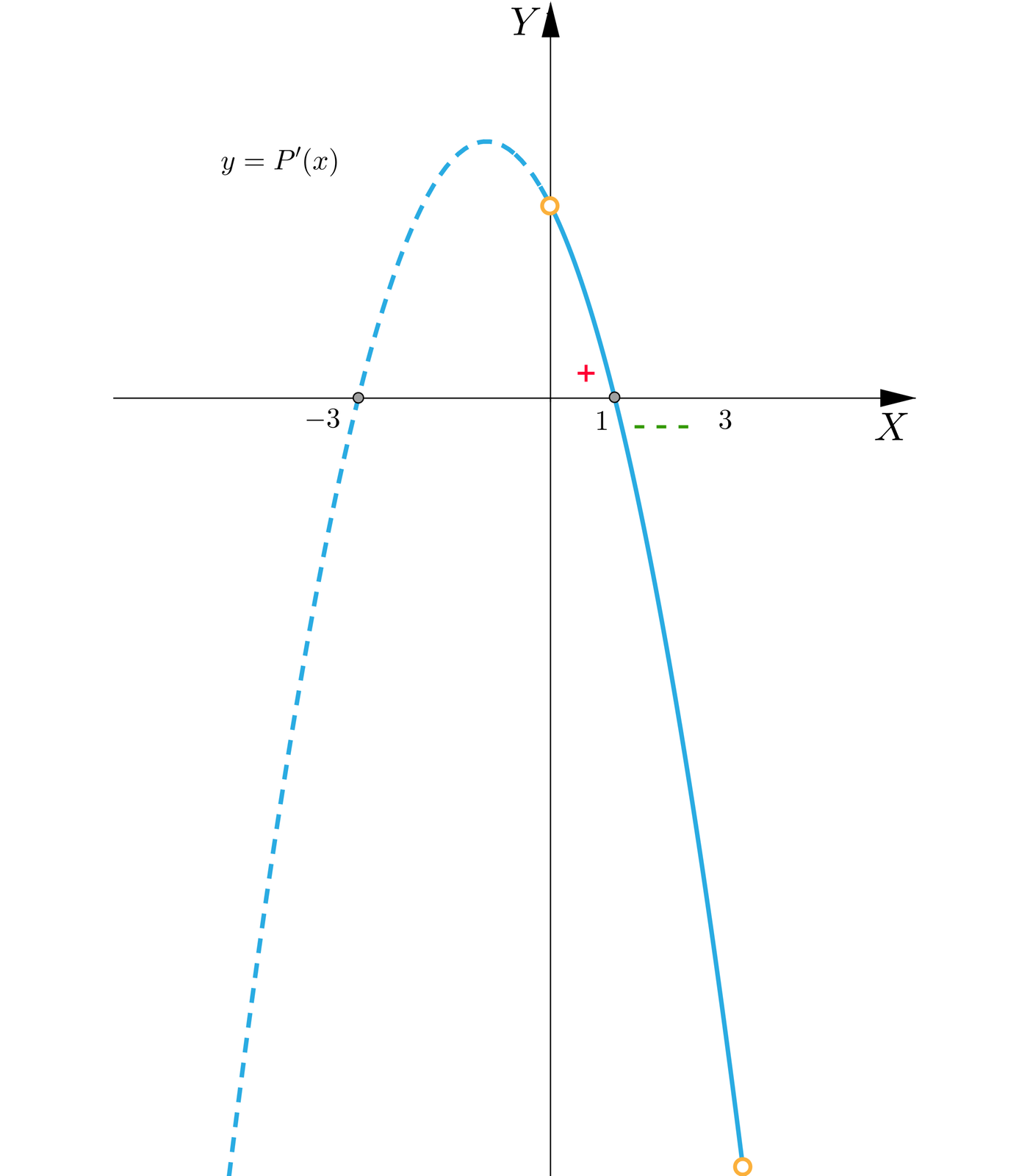
Aby wyznaczyć ekstremum, stworzymy tabelę (przedziały w tabeli są zależne od dziedziny oraz punktów, dla których pochodna się zeruje).

Funkcja osiąga maksimum dla $x=1$, zatem współrzędne wierzchołka $C\left(1,2\frac{2}{3}\right)$.

Okno ma mieć kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długości $5\ \mathrm{dm}$. Obliczymy długość dłuższej podstawy, dla której do pomieszczenia wpada jak najwięcej światła.

Rozwiązanie

Oznaczmy

R2GzQT3El81pK

Rysunek przedstawia trapez równoramienny, o krótszej podstawie równej 5, dłuższej dwa x plus 5, wysokości h i ramieniu 5.

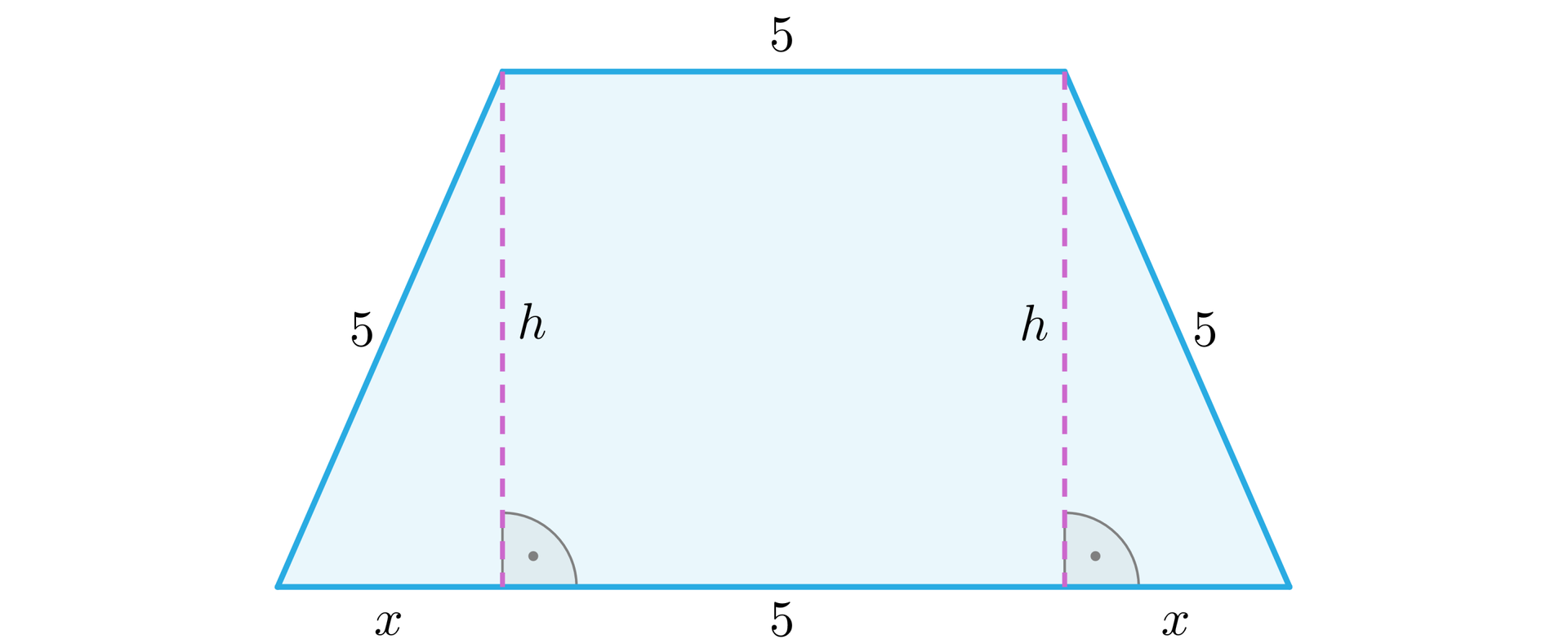
Podstawmy dane do wzoru na pole trapezu

Z twierdzenia Pitagorasa:

Podstawiając do wzoru na pole otrzymujemy:

Dziedziną tej funkcji jest zbiór:

Aby funkcja $P$ osiągała największą wartość wystarczy, by wyrażenie pod pierwiastkiem się zmaksymalizowało. Rozważmy funkcję:

Wyznaczymy pochodną funkcji $f$ korzystając ze wzoru pochodnej iloczynu dwóch funkcjipochodna iloczynu dwóch funkcjipochodnej iloczynu dwóch funkcji.

Wykonując obliczenia

$f'\left(x\right)=\left(2x+10\right)\left(25-x^2\right)+\left(x^2+10x+25\right)\left(-2x\right)=$ $=2\left(x+5\right)\left(5-x\right)\left(5+x\right)+\left(x+5\right)^2\left(-2x\right)=$$=2\left(x+5\right)^2\left(5-x\right)+\left(x+5\right)^2\left(-2x\right)=\left(x+5\right)^2\left(10-4x\right)$.

Miejsca zerowe pochodnej funkcji $f$: $x_1=-5\notin D$, $x_2=\frac{5}{2}\in D$. Naszkicujemy wykres pochodnej funkcji $f$:

R1Sarj0YzgO1C

Rysunek przedstawia wykres funkcji f od prim, oznaczono miejsca zerowe, minus 5 i dwa i pół. W dwa i pół funkcja zmienia wartości dodatnie na ujemne.

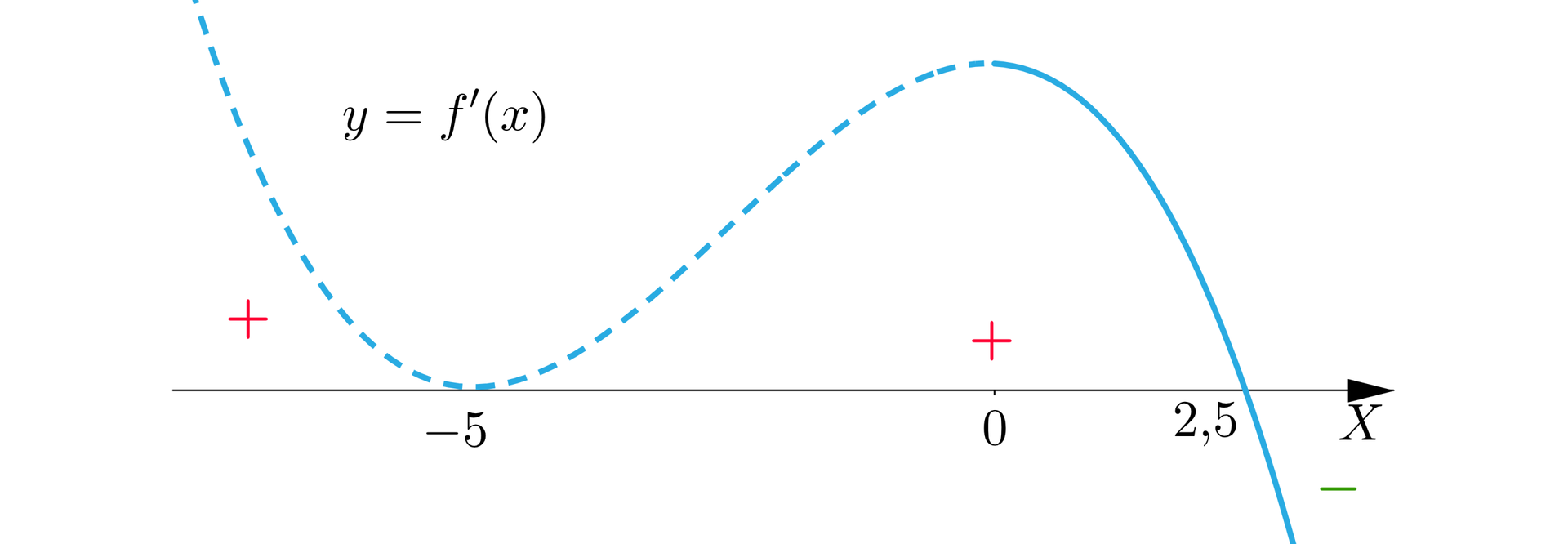
Aby wyznaczyć ekstremum stworzymy tabelę (przedziały w tabeli są zależne od dziedziny oraz punktów dla których pochodna się zeruje).

Funkcja osiąga maksimum dla $x=\frac{5}{2}$, zatem podstawa trapezu ma długość $10$.

w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej

jeśli obie funkcje $f\left(x\right)$, $g\left(x\right)$ są różniczkowalne, to pochodną iloczynu tych funkcji obliczamy według wzoru: