Przeczytaj

Definicje funkcji trygonometrycznych

Już wiesz, że między funkcjami trygonometrycznymi różnych kątów zachodzą pewne związki. Poznałeś wzory dla kątów $\frac{π}{2} - α$ . Posłużymy się nimi w tym materiale.

Niech $P = (x, y)$ będzie dowolnym punktem leżącym na końcowym ramieniu kąta skierowanego $β$ . Analizując poniższe slajdy przypomnimy definicje funkcji trygonometrycznych.

R32yhHzyPaYmK

Zajmijmy się teraz udowodnieniem poniższego twierdzenia.

o wzorach redukcyjnych dla kątów

Twierdzenie: o wzorach redukcyjnych dla kątów

Dla dowolnego kąta $α$ zachodzą równości:

$\sin (\frac{π}{2} + α) = \cos α$

$\cos (\frac{π}{2} + α) = - \sin α$

$tg (\frac{π}{2} - α) = \frac{1}{tg α}$ , o ile $tg α \neq 0$ .

Przeanalizujmy dwa dowody omawianego twierdzenia. Oba wykorzystują wzory dla kątów $\frac{π}{2} - α$ :

$\sin (\frac{π}{2} - α) = \cos α$

$\cos (\frac{π}{2} - α) = \sin α$

$tg (\frac{π}{2} - α) = \frac{1}{tg α}$ , o ile $tg α \neq 0$ .

Dowód $I$

W pierwszym dowodzie, oprócz wzorów dla kątów $\frac{π}{2} - α$ , wykorzystamy definicje funkcji trygonometrycznych. Rozważmy kąty $(\frac{π}{2} - α) i (\frac{π}{2} + α)$ i umieśćmy je w układzie współrzędnych. Dla przejrzystości zapisu oznaczmy kąt $(\frac{π}{2} - α)$ jako $β$ . Wówczas $\frac{π}{2} = α + β$ stąd $β = \frac{π}{2} - α$ . Punkt $P (x (\frac{π}{2} - α) i (\frac{π}{2} + α), y)$ jest dowolnym punktem leżącym na końcowym ramieniu kąta skierowanego $β$ natomiast punkt $P (x', y')$ leży na końcowym ramieniu kąta skierowanego $(\frac{π}{2} + α)$ .

RzraV8ClMmVK0

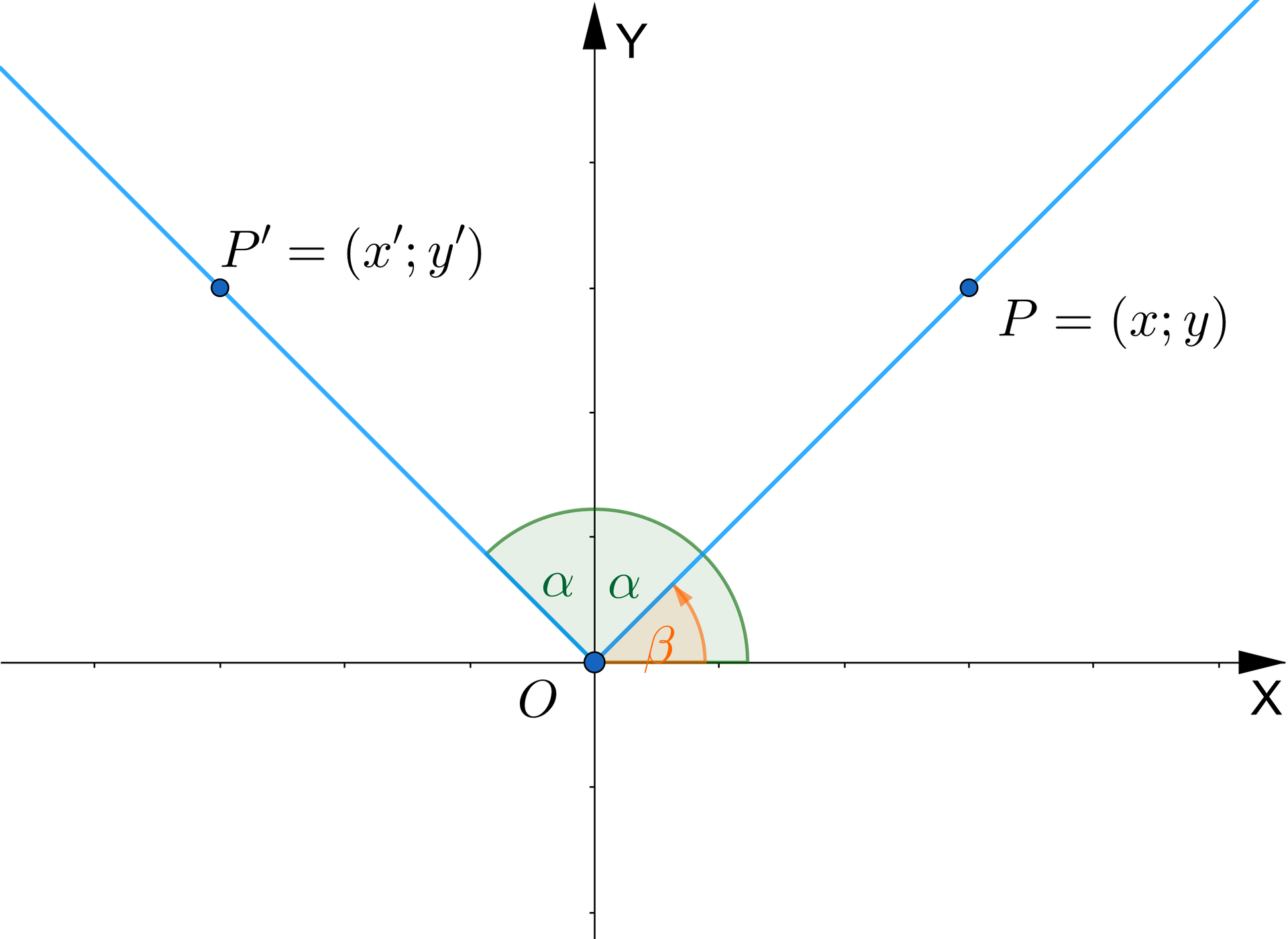
Grafika przedstawia układ współrzędnych z poziomą osią x i pionową osią y. Środek układu jest zaznaczony literą O. Na płaszczyźnie zaznaczone są 2 punkty P oraz P prim. Punkt P prim znajduje się po lewej stronie osi y, natomiast punkt P po prawej. Współrzędne punktu P prim: x';y'. Współrzędne punktu P x;y. Przez każdy z punktów przechodzi linia zaczynając się w środku układu współrzędnych. Pomiędzy osią x a linią biegnąca do punktu P zaznaczony jest kąt ostry, beta. Pomiędzy osią x a linią biegnącą do punktu P’ zaznaczony został kąt rozwarty. Ma on miarę dwa alfa plus beta.

Zauważmy, że:

$(β + α) + α = \frac{π}{2} + α$
punkty $P (x, y)$ i $P (x', y')$ są symetryczne względem osi $Y$ . Zatem $x' = - x$ a $y = y'$ . $(β + α) + α = \frac{π}{2} + α$

Otrzymujemy zatem następujące równości:

$\sin (\frac{π}{2} + α) = \frac{y'}{r} = \frac{y}{r} = \sin β = \sin (\frac{π}{2} - α) = \cos α$

$\cos (\frac{π}{2} + α) = \frac{x'}{r} = \frac{- x}{r} = - \cos β = - \cos (\frac{π}{2} - α) = - \sin α$

$tg (\frac{π}{2} + α) = \frac{y}{x} = \frac{y}{- x} = tg β = - tg (\frac{π}{2} - α) = - \frac{1}{tg α}$ .

Udowodniliśmy tym samym twierdzenie o wzorach redukcyjnych dla kątów.

Zauważmy, że wzoru $tg (\frac{π}{2} + α)$ nie musimy wyprowadzać z definicji. Możemy zastosować poznany wcześniej związek między funkcjami trygonometrycznymi tego samego kąta:

$tg α = \frac{\sin α}{\cos α}$ .

Podstawiając otrzymamy:

$tg (\frac{π}{2} + α) = \frac{\sin (\frac{π}{2} + α)}{\cos (\frac{π}{2} + α)} = \frac{\cos α}{- \sin α} = - \frac{1}{tg α} α$ .

Przejdźmy do alternatywnego dowodu.

Dowód $II$

Tym razem skorzystamy z parzystości i nieparzystości odpowiednich funkcji trygonometrycznych. Udowodnimy je na końcu tego materiału, w tym miejscu przypomnijmy jedynie, że zachodzą równości:

$\sin (- α) = - \sin α$

$\cos (- α) = \cos α$

$tg (- α) = - tg α$ .

Stąd otrzymujemy, że

$\sin (\frac{π}{2} + α) = \sin (\frac{π}{2} - (- α)) = \cos (- α) = \cos α$

$\cos (\frac{π}{2} + α) = \cos (\frac{π}{2} - (- α)) = \sin (- α) = - \sin α$

$tg (\frac{π}{2} + α) = tg (\frac{π}{2} - (- α)) = \frac{1}{tg (- α)} = - \frac{1}{tg α}$ .

Prześledzimy teraz przykłady.

Przykład 1

Wyznaczymy wartości funkcji trygonometrycznych dla kąta $\frac{5 π}{6}$ .
Wykorzystamy wyprowadzone powyżej wzory.

$\sin \frac{5 π}{6} = \sin \frac{3 π + 2 π}{6} = \sin (\frac{3 π}{6} + \frac{2 π}{6}) = \sin (\frac{π}{2} + \frac{π}{3}) = \cos \frac{π}{3} = \frac{1}{2}$
$\cos \frac{5 π}{6} = \cos (\frac{π}{2} + \frac{π}{3}) = - \sin \frac{π}{3} = \frac{- \sqrt{3}}{2}$
$tg \frac{5 π}{6} = tg (\frac{π}{2} + \frac{π}{3}) = - \frac{1}{tg \frac{π}{3}} = - \frac{1}{\sqrt{3}} = - \frac{\sqrt{3}}{3}$

Przykład 2

Doprowadzimy do najprostszej postaci wyrażenie: $\sin α + \cos (\frac{π}{2} + α) \cdot \cos^{2} α$ .

Wykorzystamy następujące wzory:

$\cos (\frac{π}{2} + α) = - \sin α$
$\sin^{2} α + \cos^{2} α = 1$ przekształconym do postaci $\sin^{2} α = 1 - \cos^{2} α$

Rozwiązanie:

$\sin α + \cos (\frac{π}{2} + α) \cdot \cos^{2} α = \sin α - \sin α \cos^{2} α =$
$= \sin α (1 - \cos^{2} α) = \sin α \sin^{2} α = \sin^{3} α$

Przykład 3

Uprościmy ułamek $\frac{\sin^{2} (\frac{π}{2} + α)}{1 - \cos (\frac{π}{2} + α)}$ .

W rozwiązaniu wykorzystamy, kolejno, wzory redukcyjnewzory redukcyjnewzory redukcyjne:

$\sin (\frac{π}{2} + α) = \cos α$
$\cos (\frac{π}{2} + α) = - \sin α$ ,

jedynkę trygonometryczną oraz wzór skróconego mnożenia:

$a^{2} - b^{2} = (a - b) (a + b)$ .

Możemy zapisać ciąg równości:

$\frac{\sin^{2} (\frac{π}{2} + α)}{1 - \cos (\frac{π}{2} + α)} = \frac{\cos^{2} α}{1 + \sin α} = \frac{1 - \sin^{2} α}{1 + \sin α} = \frac{(1 - \sin α) (1 + \sin α)}{1 + \sin α} = 1 - \sin α$ .

Zatem wyrażenie $\frac{\sin^{2} (\frac{π}{2} + α)}{1 - \cos (\frac{π}{2} + α)}$ można zapisać jako $1 - \sin α$ .

Przykład 4

Udowodnimy, że dla dowolnego kąta $α$ prawdziwa jest równość:

${(2 \sin α + \sin (\frac{π}{2} + α))}^{2} + {(- \cos (\frac{π}{2} + α) - 2 \cos α)}^{2} = 5$ .

Będziemy przekształcać lewą stronę równości tak długo, aż dojdziemy do prawej.

$L$ - lewa strona równości
$P$ - prawa strona równości

$L = {(2 \sin α + \sin (\frac{π}{2} + α))}^{2} + {(- \cos (\frac{π}{2} + α) - 2 \cos α)}^{2}$

$P = 5$

Będziemy teraz przekształcać lewą stronę wyrażenia korzystając ze wzorów $\sin (\frac{π}{2} + α) = \cos α$ . Mamy więc, że

$L = {(2 \sin α + \sin (\frac{π}{2} + α))}^{2} + {(- \cos (\frac{π}{2} + α) - 2 \cos α)}^{2} =$
$= {(2 \sin α + \cos α)}^{2} + {(- (- \sin α) - 2 \cos α)}^{2} =$
$= {(2 \sin α + \cos α)}^{2} + {(\sin α - 2 \cos α)}^{2}$

Zastosujmy teraz wzory skróconego mnożenia:

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ,

${(2 \sin α + \cos α)}^{2} = 4 \sin^{2} α + 4 \sin α \cos α + \cos^{2} α$

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ ,

${(\sin α - 2 \cos α)}^{2} = \sin^{2} α - 4 \sin α \cos α + 4 \cos^{2} α$ .

${(2 \sin α + \cos α)}^{2} + {(\sin α - 2 \cos α)}^{2} =$
$= 4 \sin^{2} α + 4 \sin α \cos α + \cos^{2} α + \sin^{2} α - 4 \sin α \cos α + 4 \cos^{2} α =$
$= 5 \sin^{2} α + 5 \cos^{2} α = 5 (\sin^{2} α + \cos^{2} α) = 5$ .

Wykazaliśmy, że $L = P$ więc równość jest prawdziwa.

Na zakończenie wróćmy do dowodu nieparzystości funkcji sinus i tangens oraz parzystości funkcji cosinus. Chcemy pokazać, że dla dowolnego kąta $α$ zachodzą równości:

$\sin (- α) = - \sin α$
$\cos (- α) = \cos α$
$tg (- α) = - tg α$

Narysujmy w układzie współrzędnych kąty skierowane $α$ i $-α$ oraz zaznaczmy punkty $P (x, y)$ i $P (x', y')$ na ich ramionach końcowych.

RxnTRmq22gi3B

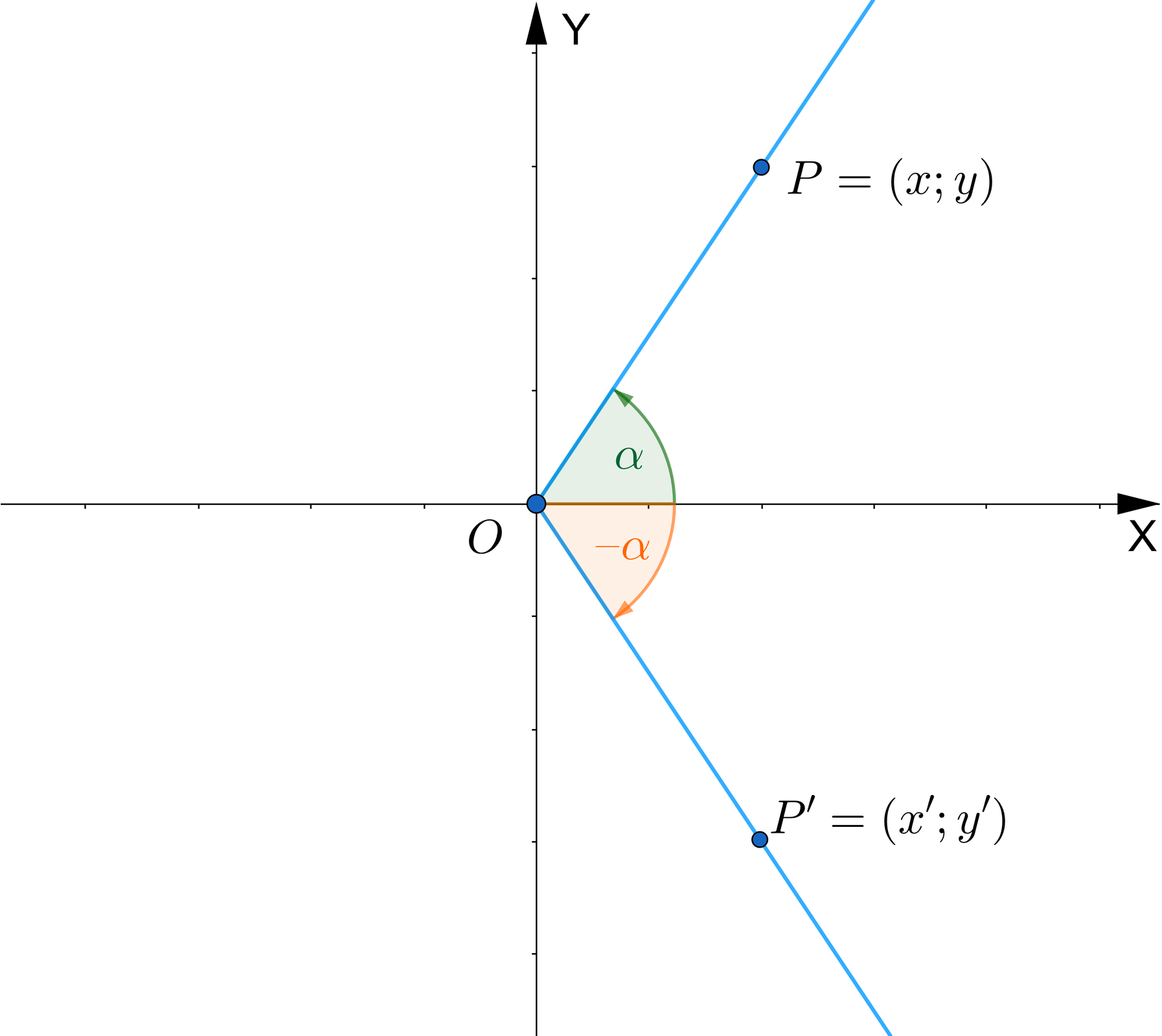
Zauważmy, że punkty $P (x, y)$ i $P (x', y')$ są symetryczne względem osi $X$ . Zatem $x' = x$ a $y' = - y$

$\sin (- α) = \frac{y'}{r} = \frac{- y}{r} = \sin α$
$\cos (- α)$
$tg (- α) = \frac{y'}{x'} = \frac{- y}{x} = α$

Udowodniliśmy zastosowane wzory.

Ważne!

Oprócz poznanych przez Ciebie funkcji trygonometrycznych są również dwie funkcje teraz już rzadko używane: secans i cosecans. Choć islamscy matematycy używali je już w X wieku, to w Europie funkcję secans wprowadził dopiero Mikołaj Kopernik w dziele „O obrotach sfer niebieskich”.

Słownik

wzory redukcyjne

wzory pozwalające wyrazić wartości funkcji trygonometrycznych dowolnego kąta $α$ za pomocą wartości funkcji kąta ostrego

Wprowadzenie

Animacja

Definicje funkcji trygonometrycznych

Dowód $I$

Dowód $II$

Słownik

Wprowadzenie

Animacja

Przeczytaj

Definicje funkcji trygonometrycznych

Dowód I

Dowód II

Słownik

Dowód $I$

Dowód $II$