Przeczytaj
Omówimy kilka szczególnych rodzajów kątów pomiędzy odcinkami w prostopadłościanieprostopadłościanie.
Czasami do wyznaczenia miar kątów będziemy używali funkcji trygonometrycznych.
W wyznaczaniu miar kątów będą pomocne trójkąty, które przedstawiono na poniższych rysunkach.
1. Kąt między przekątną prostopadłościanu a przekątną podstawy

Do wyznaczenia miary kąta posłużymy się trójkątem prostokątnym o przyprostokątnych, którymi są krawędź boczna i przekątna podstawy prostopadłościanu oraz przeciwprostokątnej, będącej przekątną prostopadłościanu.
2. Kąt między przekątną prostopadłościanu a krawędzią boczną
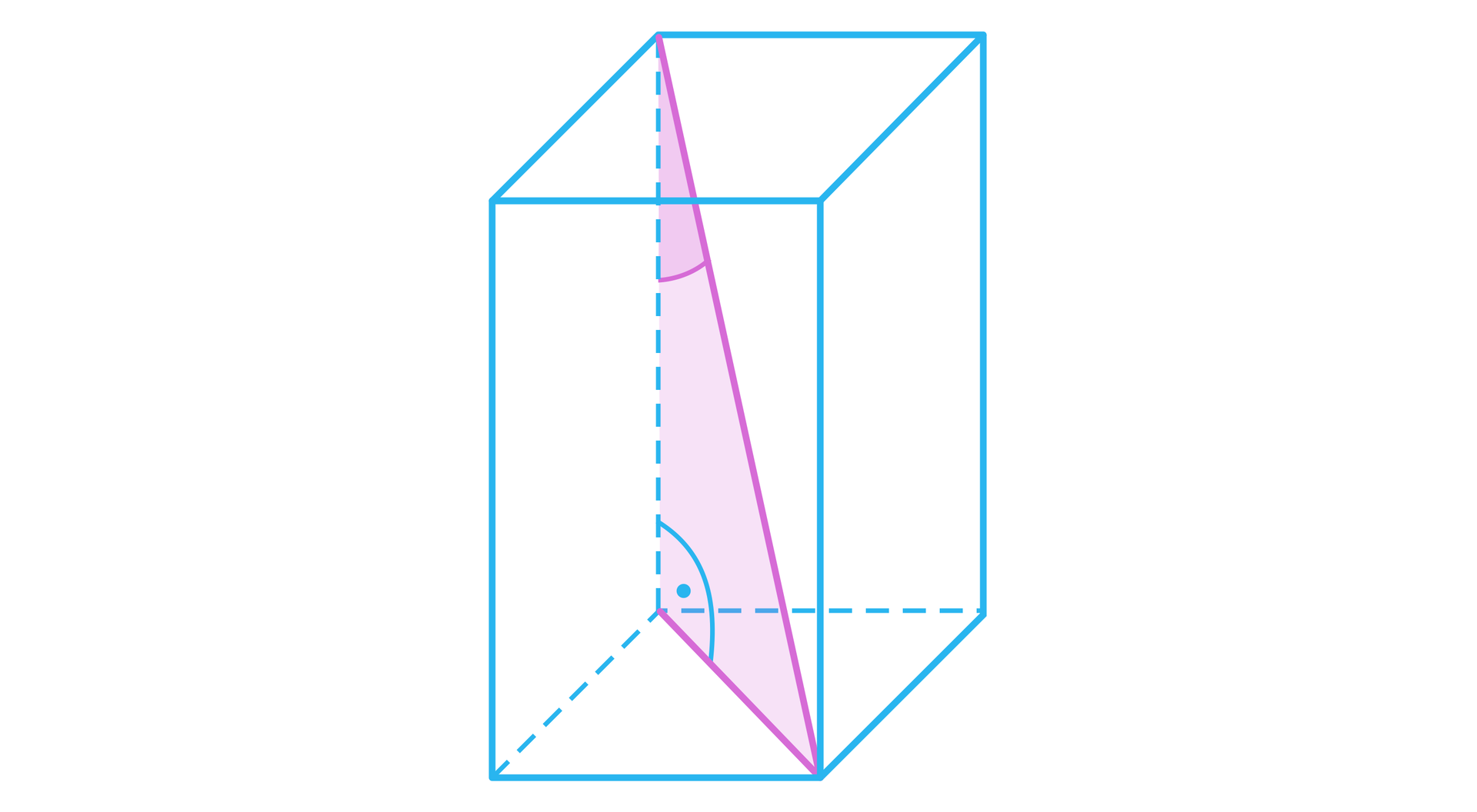
Trójkąt prostokątny, z którego korzystamy do wyznaczenia miary kąta, jest zbudowany z tych samych odcinków, jak w pierwszym przypadku.
3. Kąt między przekątną prostopadłościanu a przekątną ściany bocznej
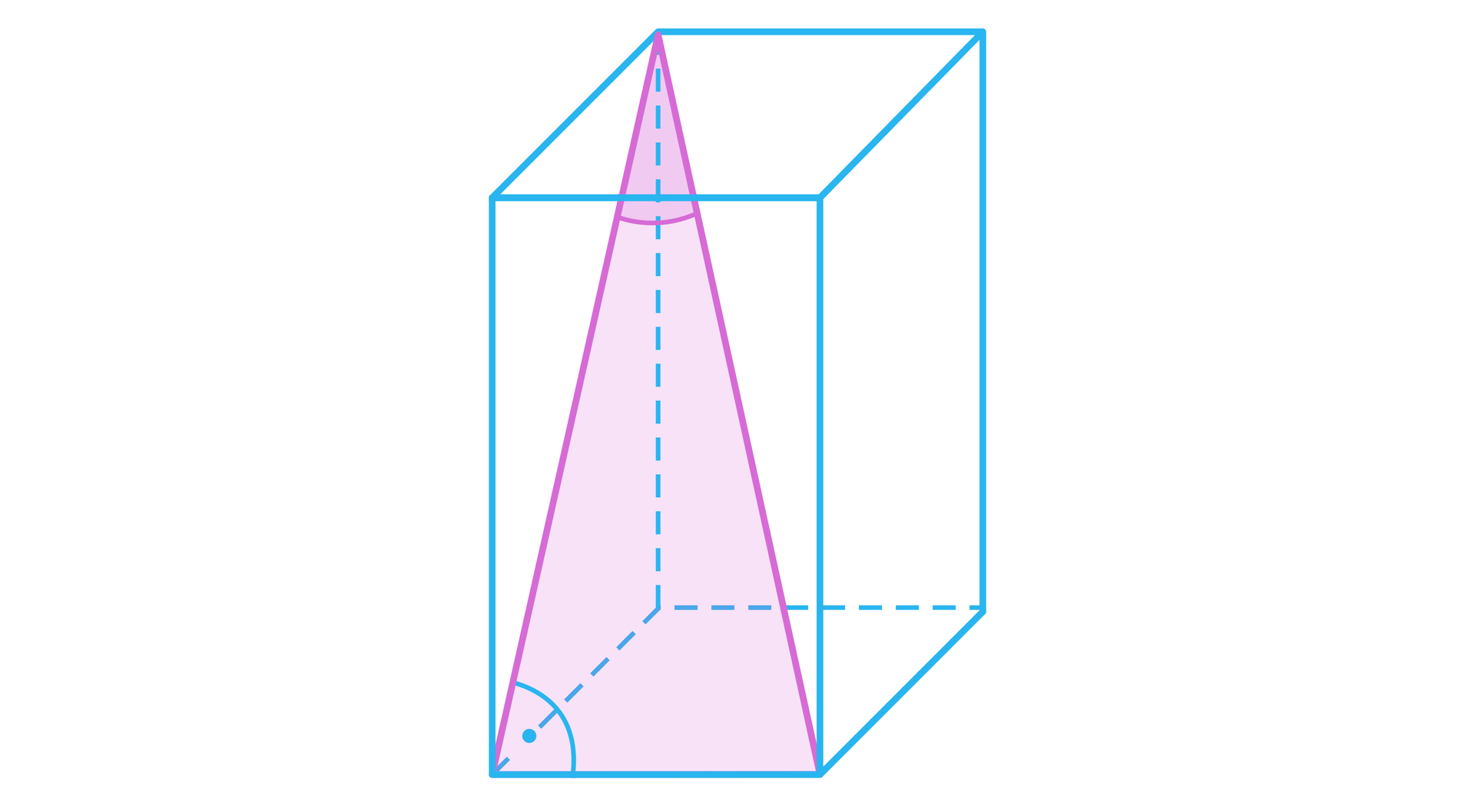
Trójkąt prostokątny, którego używamy do wyznaczenia miary kąta jest zbudowany z przyprostokątnych, którymi są krawędź podstawy prostopadłościanu i przekątna ściany bocznej oraz przeciwprostokątnej, która jest przekątną prostopadłościanu.
4. Kąt między przekątnymi prostopadłościanu

Do wyznaczenia miary kąta posłużymy się trójkątem równoramiennym, którego podstawa jest równa długości przekątnej podstawy prostopadłościanu lub długości krawędzi bocznej, a ramionami odcinki, które są równe połowie długości każdej z przekątnych prostopadłościanu.
5. Kąt między przekątnymi sąsiednich ścian bocznych

Do wyznaczenia miary kąta posłużymy się trójkątem, którego podstawą jest odcinek będący przekątną podstawy prostopadłościanu, a pozostałe dwa boki są równe długościom przekątnych sąsiednich ścian bocznych prostopadłościanu.
Krawędzie prostopadłościanu mają długości: , , . Wyznaczymy miarę kąta nachylenia przekątnej tego prostopadłościanu do przekątnej jego podstawy.
Rozwiązanie:
Narysujmy prostopadłościan, zaznaczmy odpowiedni kąt i wprowadźmy oznaczenia, jak na poniższym rysunku.

Jeżeli przez oznaczymy długość przekątnej podstawy prostopadłościanu, to korzystając z twierdzenia Pitagorasa, mamy:
,
,
.
Korzystając z trójkata prostokątnego z poniższego rysunku, mamy:

.
Miarę kąta odczytujemy z tablic wartości funkcji trygonometrycznych.
Zatem .
Wiadomo, że kąt między przekątną prostopadłościanu a krawędzią boczną ma miarę . Wyznaczymy sumę długości krawędzi tego prostopadłościanu, jeżeli przekątna prostopadłościanu ma długość , a jedna z krawędzi podstawy jest dwa razy dłuższa od drugiej.
Rozwiązanie:
Narysujmy prostopadłościan i wprowadźmy oznaczenia.
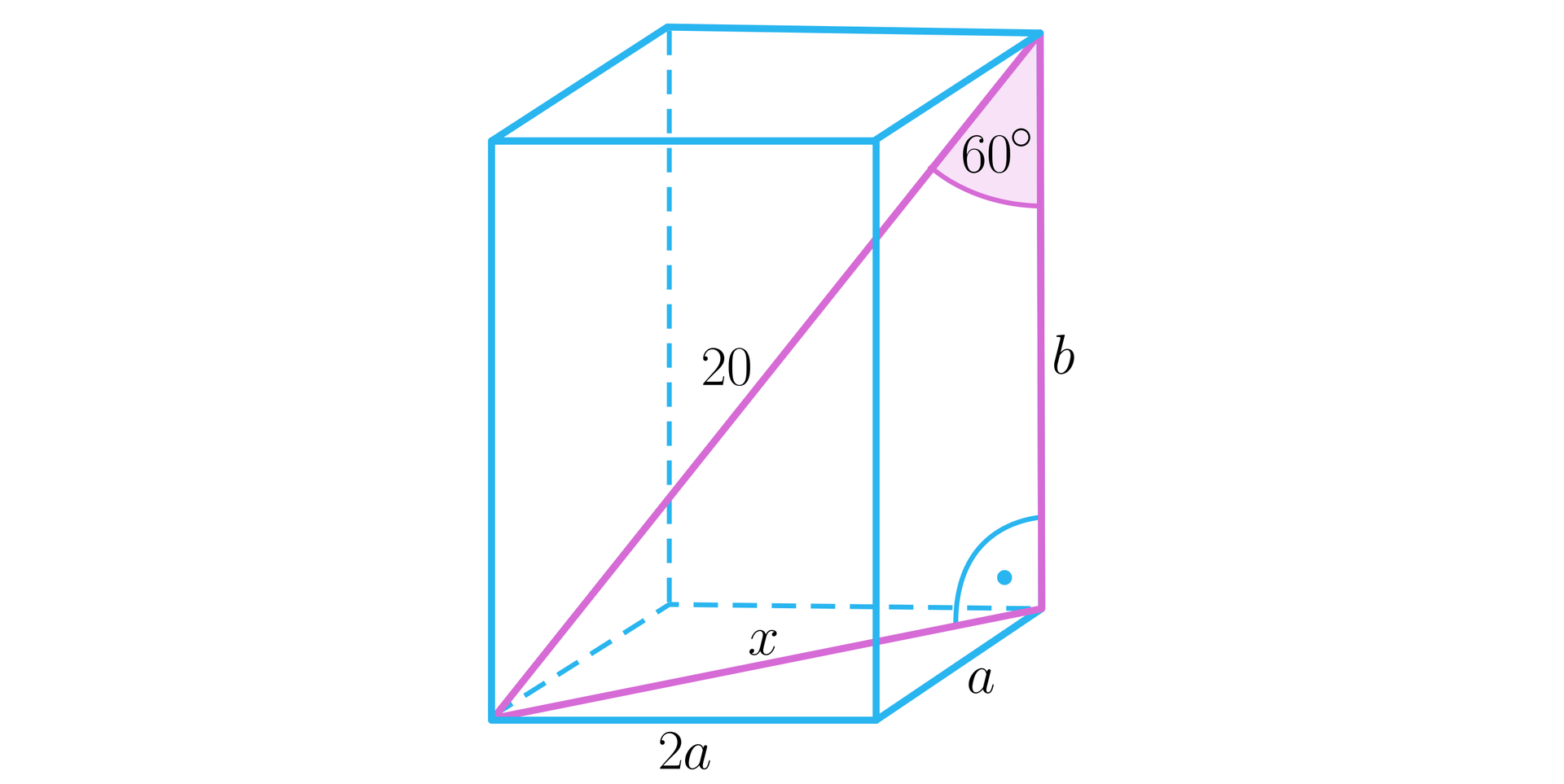
Zauważmy, że otrzymujemy trójkąt prostokątny o kątach , , , zatem:
,
.
Do wyznaczenia wartości wykorzystujemy twierdzenie Pitagorasa i rozwiązujemy równanie:
stąd:
, czyli
Krawędzie podstawy prostopadłościanu mają długości i .
Wobec tego suma długości krawędzi tego prostopadłościanu jest równa:
.
Wyznaczymy miarę kąta nachylenia przekątnej prostopadłościanu do przekątnej ściany o największej powierzchni, jeżeli długości krawędzi prostopadłościanu pozostają w stosunku .
Rozwiązanie:
Jeżeli długości krawędzi prostopadłościanu pozostają w stosunku , to ich długości możemy wyrazić za pomocą wielkości , gdzie .
Zatem ściana o największej powierzchni ma wymiary oraz .
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.
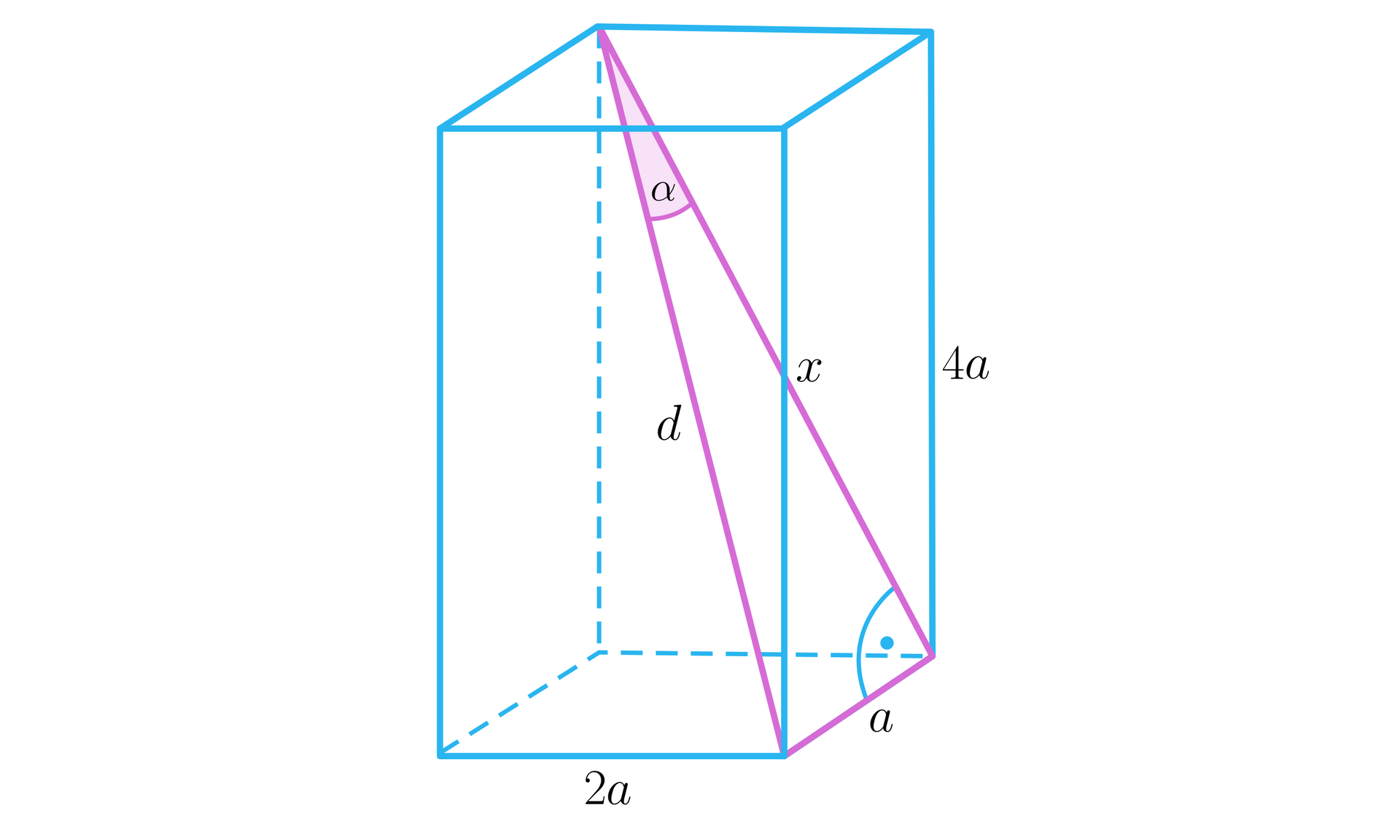
Ponieważ jest długością przekątnej prostopadłościanu, zatem korzystając ze wzoru na długość przekątnej prostopadłościanu, mamy:
Rozpatrzmy trójkąt prostokątny, jak na poniższym rysunku.
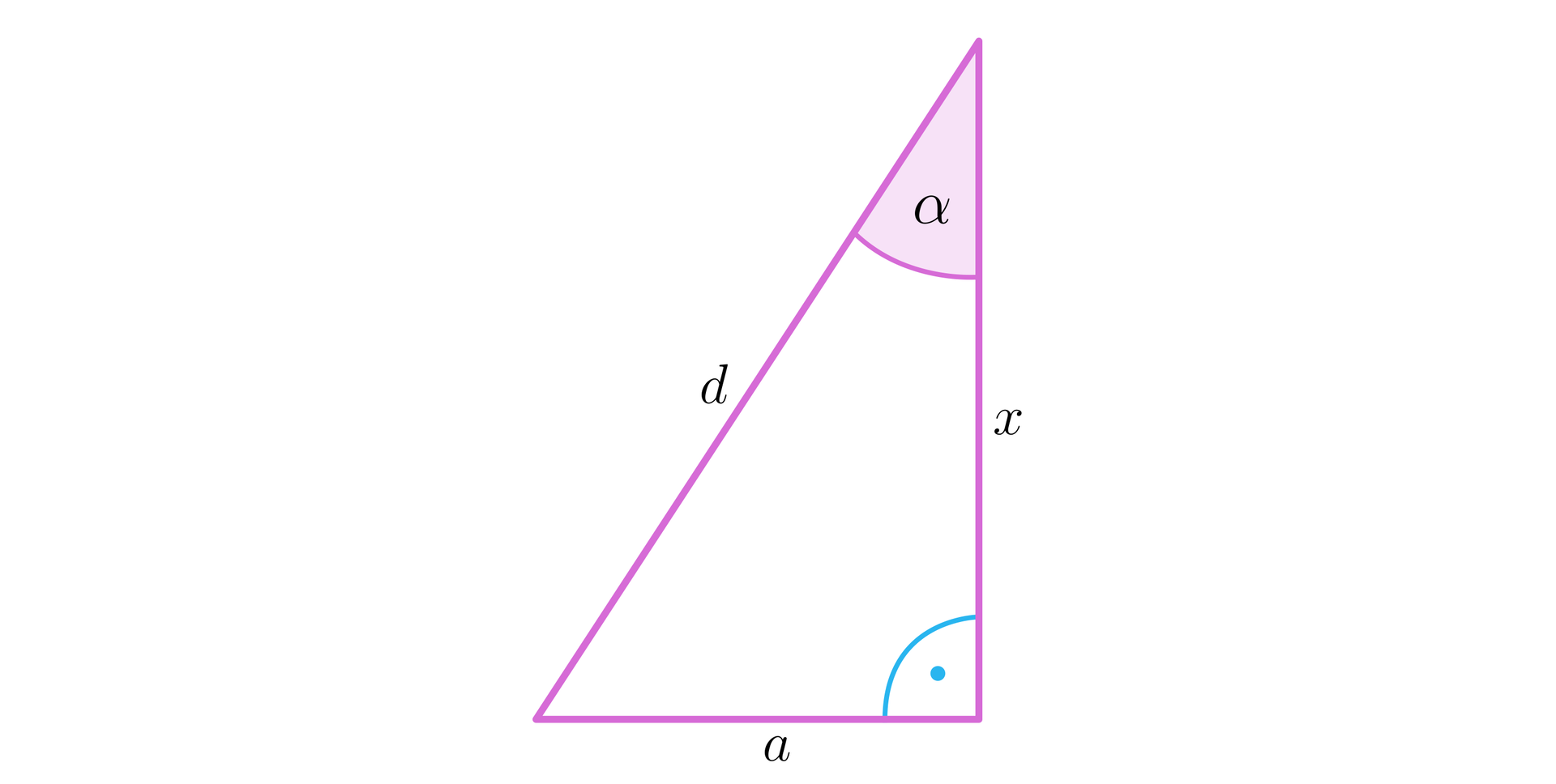
Zatem korzystając z funkcji trygonometrycznej sinus mamy:
Wobec tego, jeżeli wykorzystujemy tablice wartości funkcji trygonometrycznych, to .
Wiadomo, że kąt między przekątną prostopadłościanu o podstawie kwadratowej, a przekątną ściany bocznej ma miarę . Wyznaczymy długości krawędzi tego prostopadłościanu, jeżeli przekątna ściany bocznej ma długość .
Rozwiązanie:
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.
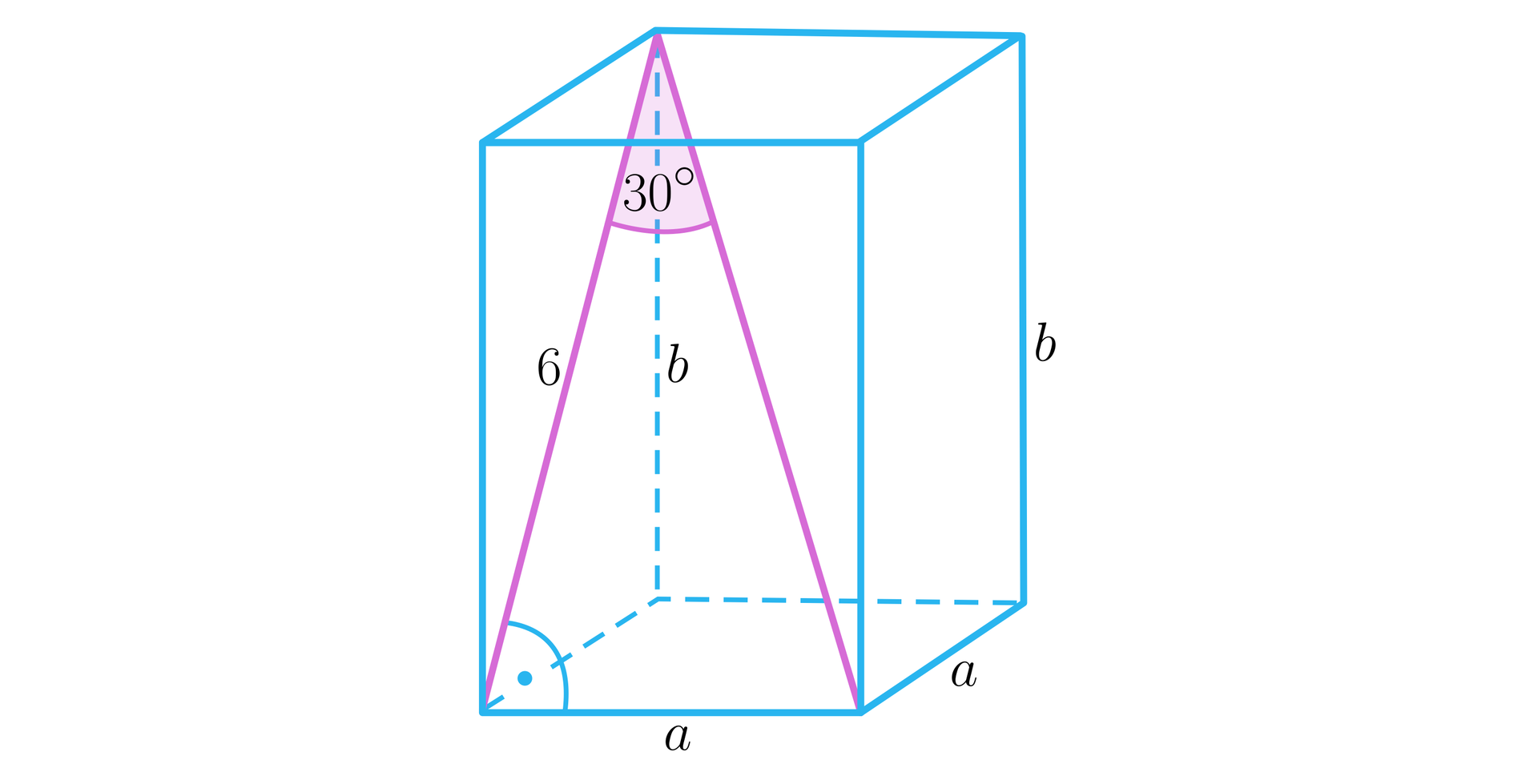
Z trójkąta o kątach , , otrzymujemy, że .
Korzystając z twierdzenia Pitagorasa do wyznaczenia wartości rozwiązujemy równanie:
,
,
, czyli .
Krawędź podstawy rozpatrywanego prostopadłościanu ma długość , a krawędź boczna ma długość .
Wyznaczymy miarę kąta ostrego między przekątnymi prostopadłościanu, w którym krawędzie podstawy mają długości i , a krawędź boczna ma długość .
Rozwiązanie:
Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na rysunku.
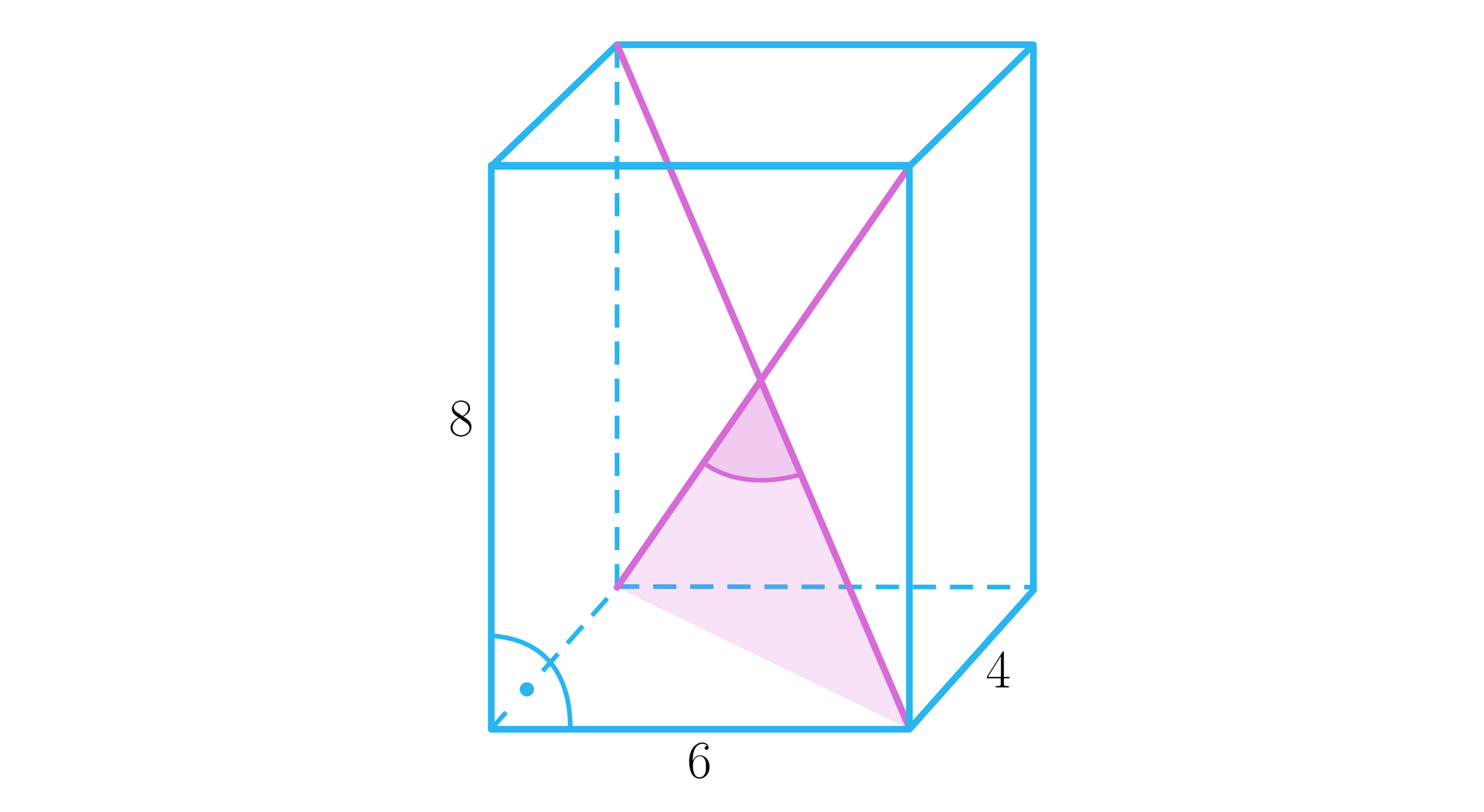
Niech będzie długością przekątnej prostopadłościanu. Korzystając ze wzoru na długość przekątnej prostopadłościanu mamy:
.
Jeżeli przez oznaczymy długość przekątnej podstawy prostopadłościanu, to .
Do wyznaczenia miary kąta pomiędzy przekątnymi prostopadłościanu rozpatrujemy trójkąt równoramienny, którego długość podstawy jest równa długości przekątnej podstawy prostopadłościanu, a długości ramion są równe połowie długości przekątnej prostopadłościanu.
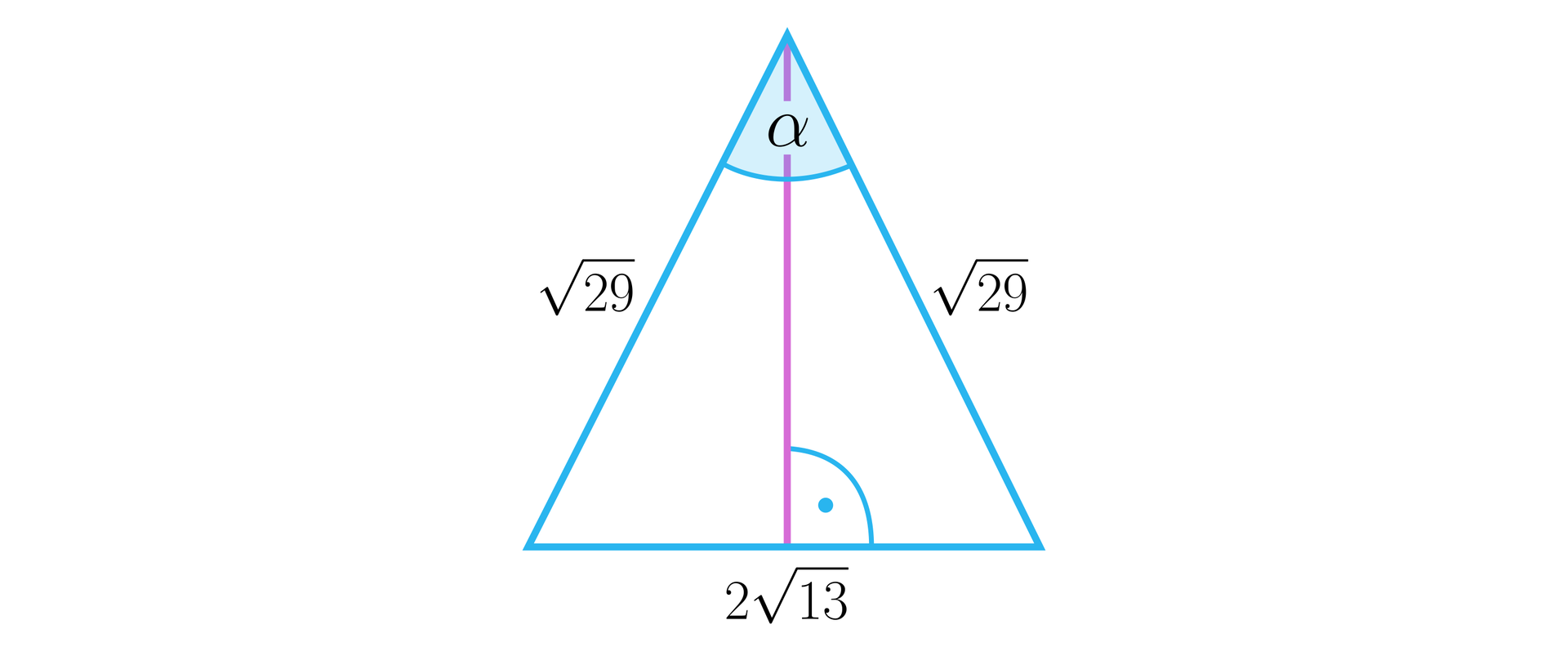
Do wyznaczenia miary kąta zastosujemy twierdzenie cosinusów.
Zatem:
,
stąd:
,
.
Jeżeli wykorzystujemy tablice wartości funkcji trygonometrycznych, to .
Wyznaczymy miarę kąta pomiędzy przekątnymi sąsiednich ścian bocznych prostopadłościanu, którego podstawa ma wymiary na a krawędź boczna ma długość .
Rozwiązanie:
Narysujmy prostopadłościan i wprowadźmy odpowiednie oznaczenia.
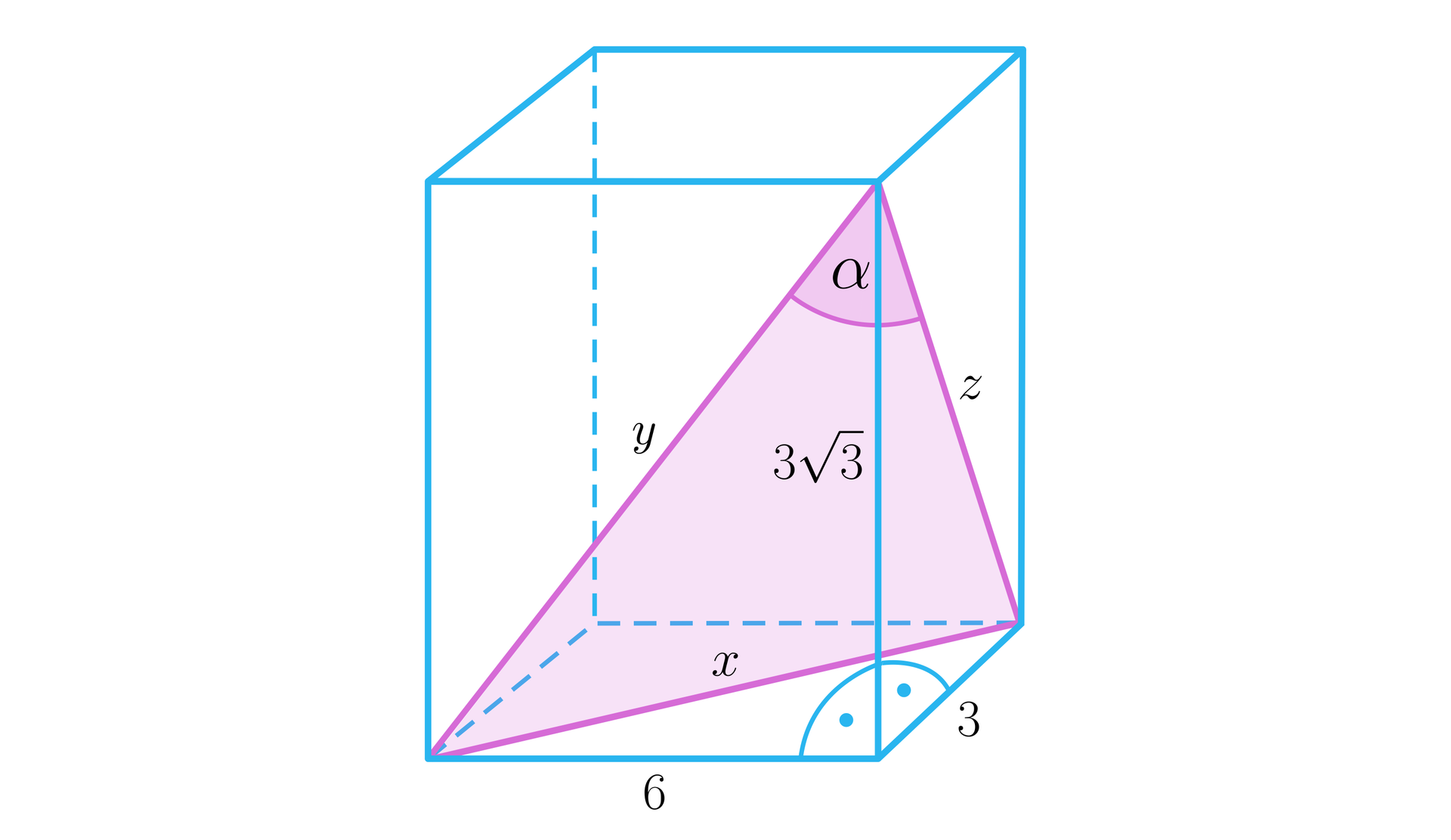
Jeżeli przez oznaczymy długość przekątnej podstawy prostopadłościanu, to korzystając z twierdzenia Pitagorasa rozwiązujemy równanie:
Zatem .
Jeżeli przez i oznaczymy długości przekątnych ścian bocznych prostopadłościanu, to korzystając z twierdzenia Pitagorasa rozwiązujemy równania:
, zatem
, zatem
Niech będzie miarą kąta pomiędzy przekątnymi sąsiednich ścian bocznych prostopadłościanu.
Wówczas miarę tego kąta wyznaczymy z twierdzenia cosinusów, korzystając z trójkąta z poniższego rysunku.
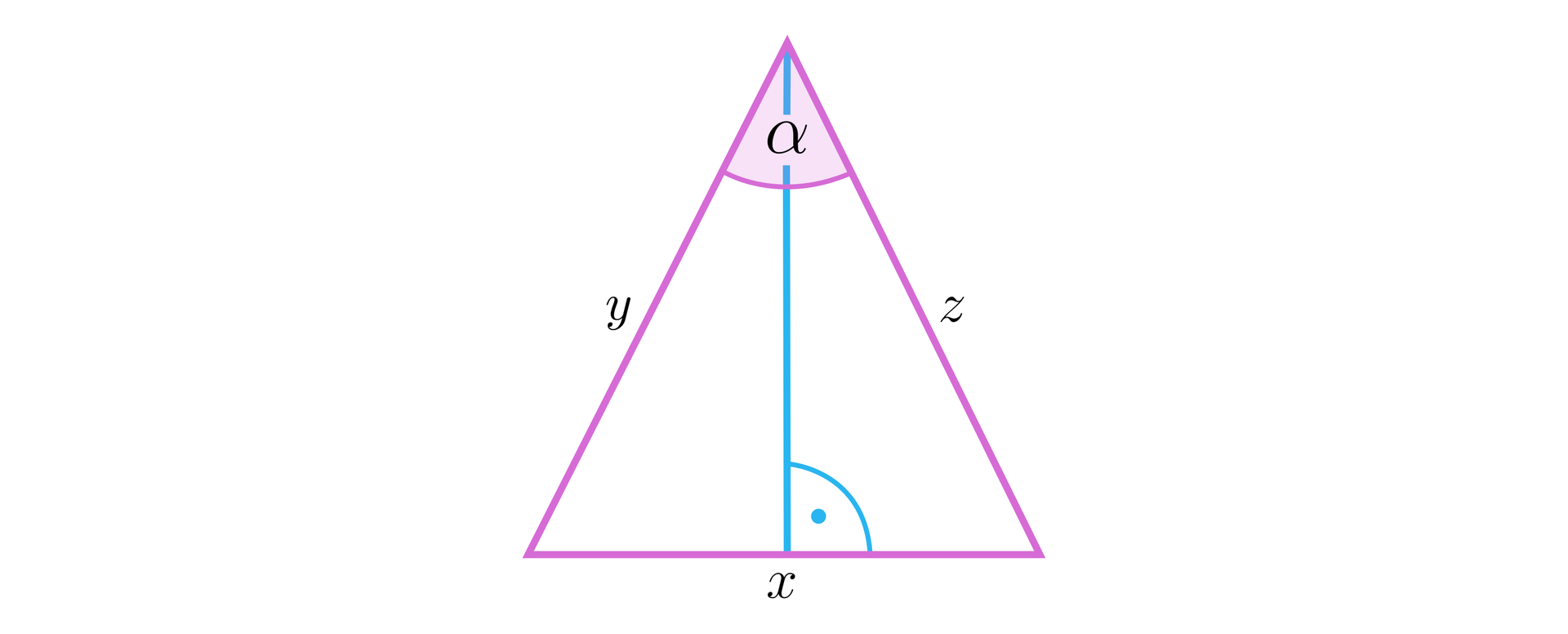
Wobec tego mamy:
Zatem:
Jeżeli wykorzystujemy tablice wartości funkcji trygonometrycznych, to .
Słownik
równoległościan, którego każda ściana jest prostokątem