Przeczytaj
Jeśli chcemy udowodnić, że dany kąt jest kątem prostym na płaszczyźnie, możemy użyć twierdzenia odwrotnego do twierdzenia Pitagorasa. Mówi ono, że jeśli suma kwadratów długości dwóch krótszych boków trójkąta jest równa kwadratowi długości najdłuższego boku, to trójkąt ten jest prostokątny. Wiadomo również, że kątem prostym jest wtedy kąt leżący naprzeciw najdłuższego boku. Twierdzenie to jest jednym z narzędzi pozwalającym badać prostopadłość prostych. W tym materiale poznamy kolejne twierdzenie mówiące, kiedy dwie proste są prostopadłe. Zanim przejdziemy do omówienia samego twierdzenia i jego dowodu przypomnijmy pewne fakty.
Prosta jest prostopadła do płaszczyzny , jeżeli jest prostopadła do każdej prostej zawierającej się w płaszczyźnie i przechodzącej przez punkt wspólny prostej i płaszczyzny .
Rzutem prostopadłym punktu na płaszczyznę jest punkt przecięcia prostej prostopadłej do tej płaszczyzny przechodzącej przez ten punkt z tą płaszczyzną.
Dane są przecinające się płaszczyzny i . Jeżeli prosta zawarta w płaszczyźnie jest prostopadła do dwóch prostych i zawartych w płaszczyźnie , gdzie proste , i przecinają się w jednym punkcie, to płaszczyzna jest prostopadła do płaszczyzny .
Dana jest płaszczyzna i prosta przecinająca tę płaszczyznę w punkcie . Niech będzie rzutem prostopadłymrzutem prostopadłym prostej na płaszczyznę . Wtedy prosta zawarta w płaszczyźnie i przechodząca przez punkt jest prostopadła do prostej wtedy i tylko wtedy, gdy jest prostopadła do prostej , czyli
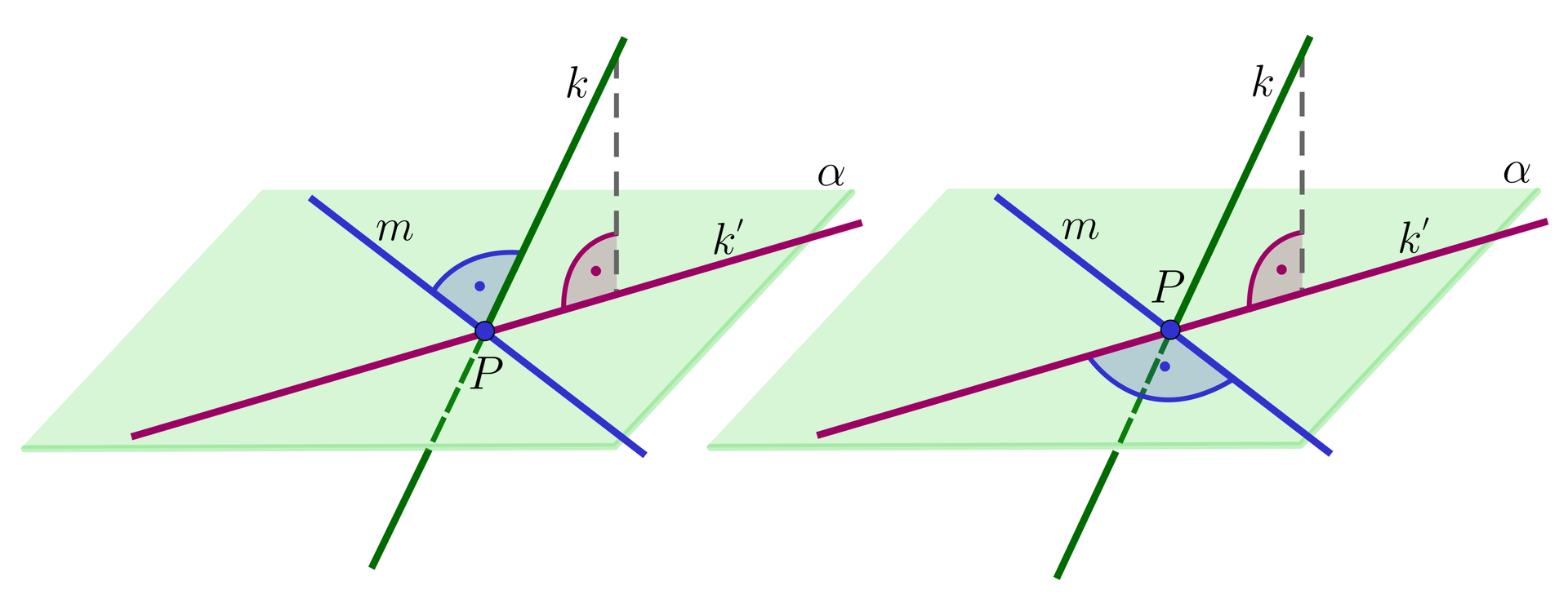
Ponieważ prosta jest rzutem prostej na płaszczyznę , więc płaszczyzna wyznaczona przez proste i jest prostopadła do płaszczyzny .
Oznaczmy tę płaszczyznę przez .
Poprowadźmy prostą zawartą w płaszczyźnie , prostopadłą do prostej i przechodzącą przez punkt . Wtedy prosta jest prostopadła do płaszczyzny . Zatem prosta jest prostopadła do prostej .
Jeśli prosta jest prostopadła do prostej , to jest prostopadła do płaszczyzny , gdyż jest prostopadła do dwóch prostych zawartych w tej płaszczyźnie: i . Stąd prosta jest prostopadła do każdej prostej zawartej w płaszczyźnie , w szczególności do prostej .
Jeśli prosta jest prostopadła do prostej , to jest prostopadła do płaszczyzny , gdyż jest prostopadła do dwóch prostych zawartych w tej płaszczyźnie: i . Stąd prosta jest prostopadła do każdej prostej zawartej w płaszczyźnie , w szczególności do prostej .
Na płaszczyźnie dane są dwa punkty i . Przez punkt przechodzi prosta nachylona pod kątem do płaszczyzny . Na prostej dany jest punkt , którego rzutem prostopadłymrzutem prostopadłym na płaszczyznę jest punkt .
Wiedząc, że , i obliczymy odległość pomiędzy punktami i .
Rozwiązanie
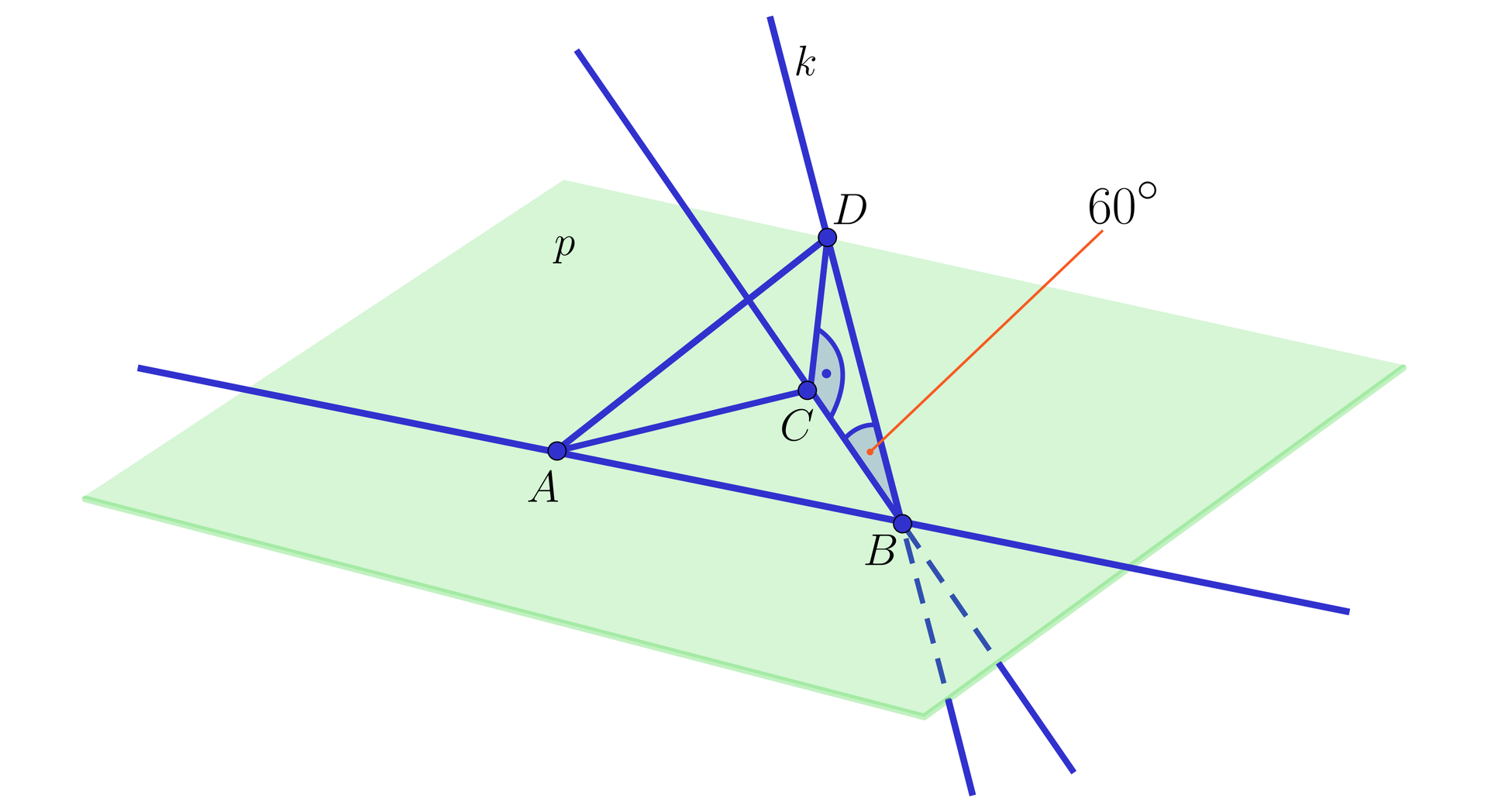
Zauważmy, że , więc z twierdzenia odwrotnego do twierdzenia Pitagorasa kąt jest kątem prostym.
Ponieważ prosta jest prostopadła do prostej , więc z twierdzenia o trzech prostych prostopadłych prosta jest prostopadła do prostej , czyli trójkąt jest trójkątem prostokątnym.
Z trójkąta prostokątnego otrzymujemy , czyli .
Z trójkąta prostokątnego otrzymujemy .
Na płaszczyźnie dane są dwa punkty i . Przez punkt przechodzi prosta nachylona pod kątem do płaszczyzny . Na prostej dany jest punkt , którego rzutem prostopadłym na płaszczyznę jest punkt . Wiedząc, że i pole trójkąta wynosi obliczymy pole trójkąta .
Rozwiązanie
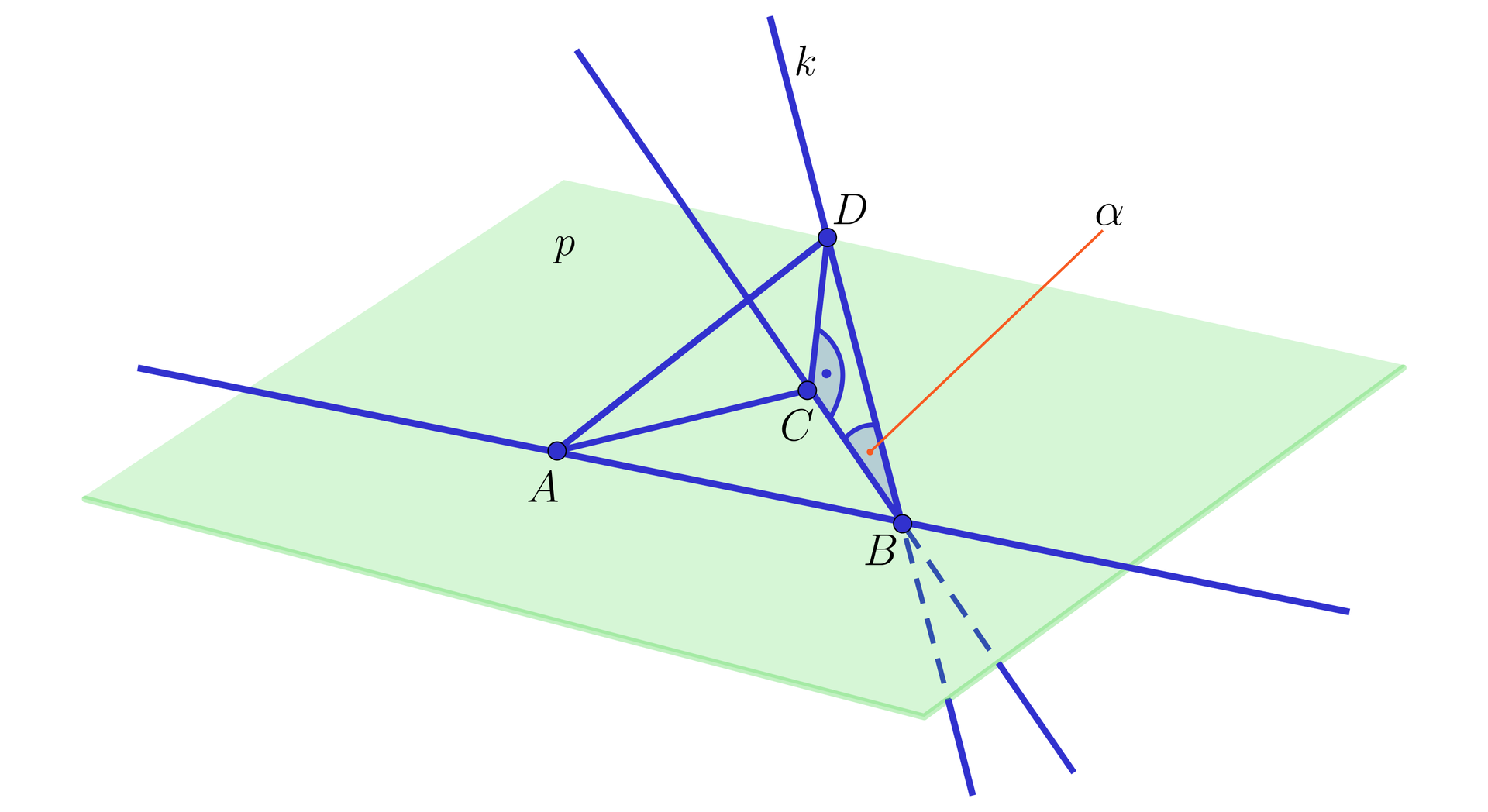
Oznaczmy przez kąt . Wówczas , czyli . Stąd .
Ponieważ prosta jest prostopadła do prostej , więc z twierdzenia o trzech prostych prostopadłych prosta jest prostopadła do prostej .
Z trójkąta prostokątnego otrzymujemy , czyli . Pole trójkąta prostokątnego wynosi .
Na płaszczyźnie dane są dwa punkty i . Przez punkt przechodzi prosta . Na prostej dany jest punkt , którego rzutem prostopadłym na płaszczyznę jest punkt . Wiedząc, że prosta jest prostopadła do prostej oraz stosunek pola trójkąta do pola trójkąta wynosi wyznaczymy kąt, pod jakim prosta nachylona jest do płaszczyzny .
Rozwiązanie
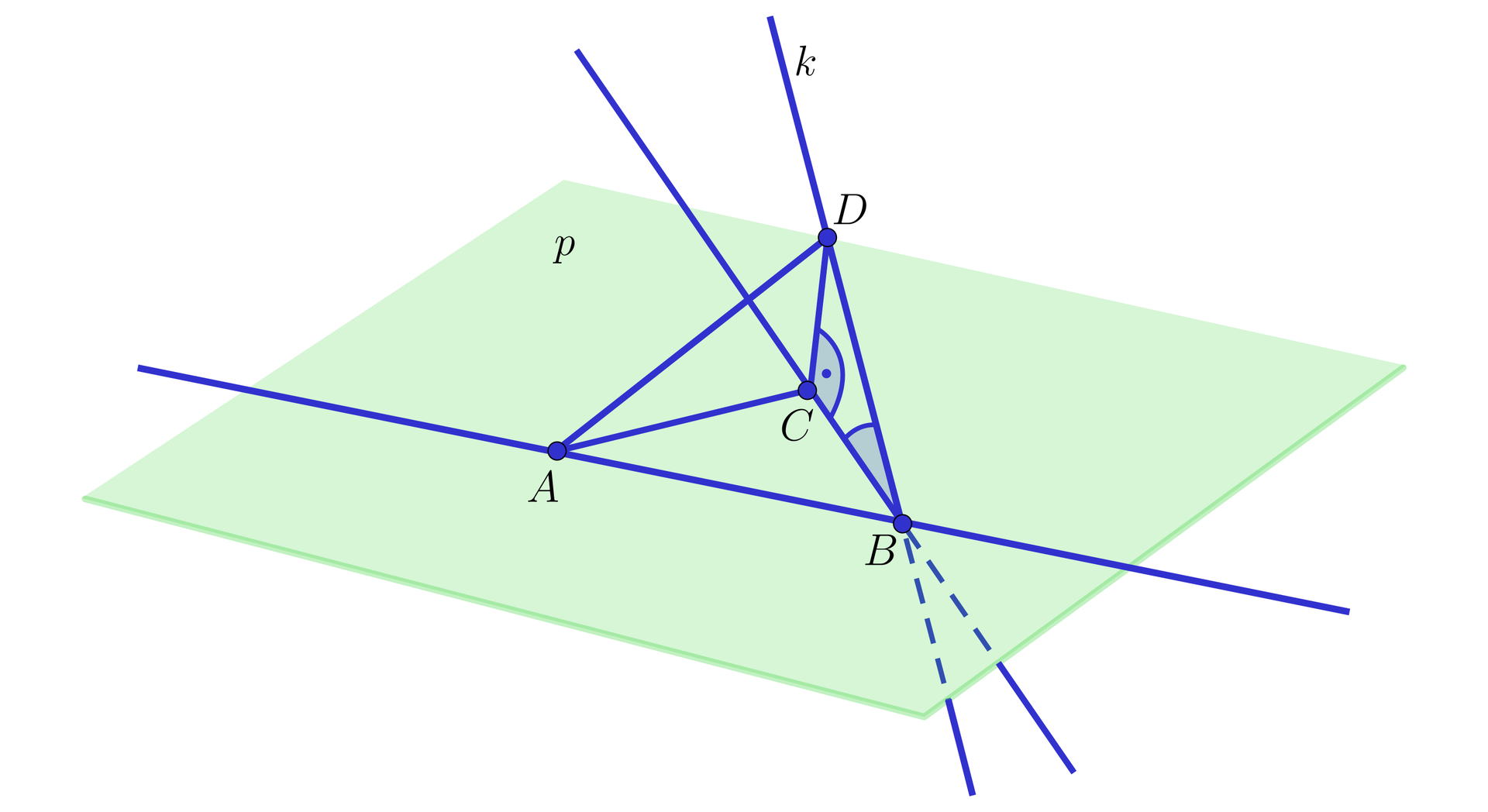
Ponieważ prosta jest prostopadła do prostej , więc z twierdzenia o trzech prostych prostopadłych prosta jest prostopadła do prostej .
Oznaczmy kąt trójkąta prostokątnego przez . Kąt ten jest również kątem nachylenia prostej do płaszczyzny .
Ponieważ trójkąty i są prostokątne, więc . Stąd .
Prosta przecina płaszczyznę pod kątem spełniającym równanie , gdzie .
Dane są trzy punkty , i takie, że . Punkt jest środkiem odcinka . Dany jest punkt taki, że prosta jest prostopadła do prostej . Uzasadnimy, że rzut prostopadły punktu na płaszczyznę należy do prostej .
Rozwiązanie
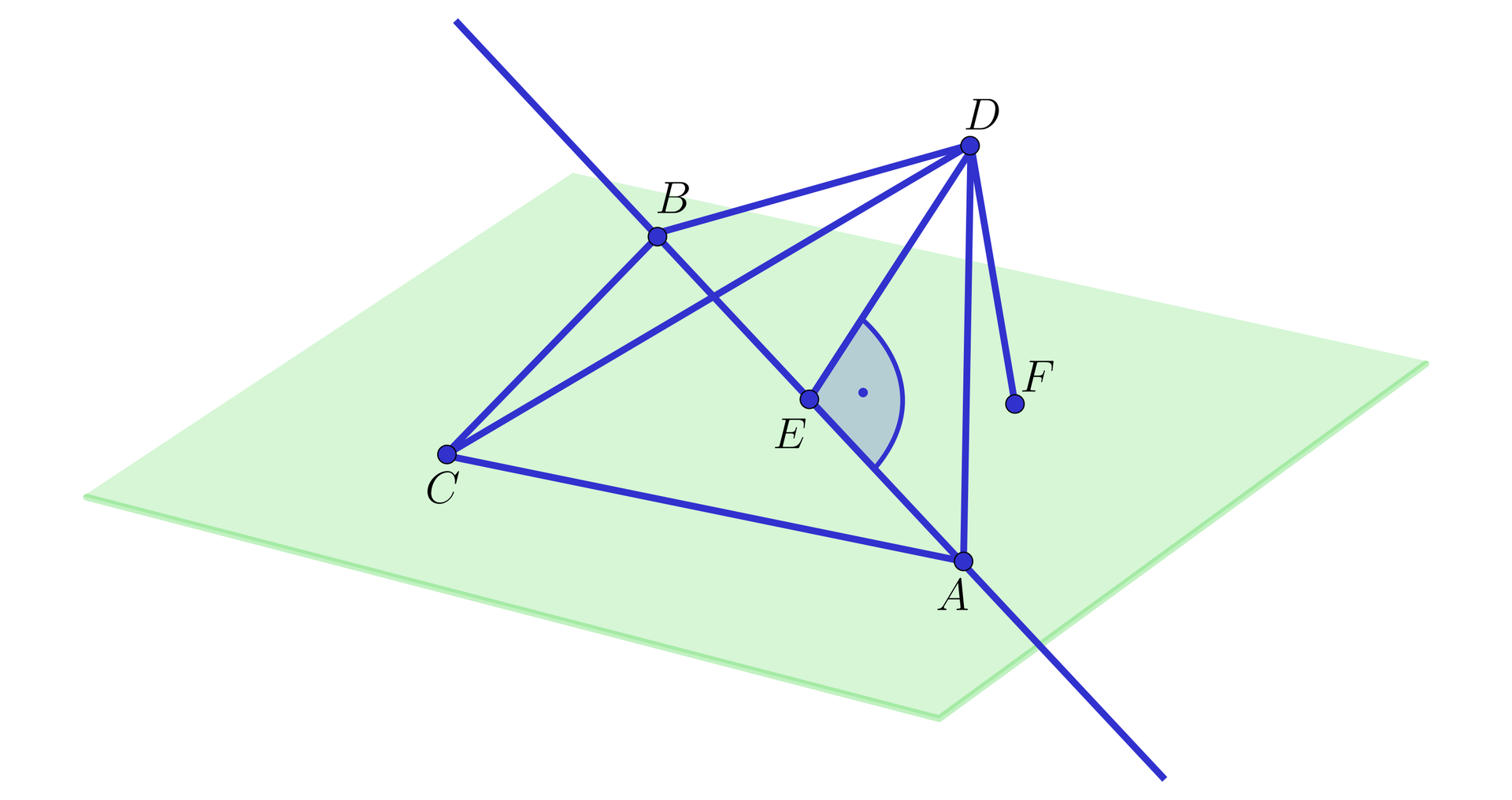
Ponieważ trójkąt jest trójkątem równoramiennym , więc prosta jest prostopadła do prostej .
Niech punkt będzie rzutem prostopadłym punktu na płaszczyznę .
Ponieważ prosta jest prostopadła do prostej , więc z twierdzenia o trzech prostych prostopadłych jest prostopadła do .
Proste , i leżą w jednej płaszczyźnie oraz prosta jest prostopadła do prostej oraz . Zatem proste i się pokrywają. Stąd punkt leży na prostej .
Słownik
punkt przecięcia prostej prostopadłej do tej płaszczyzny przechodzącej przez ten punkt z tą płaszczyzną