Przeczytaj

Rozpoczniemy od przesuwania punktów wzdłuż osi $Y$ .

Przykład 1

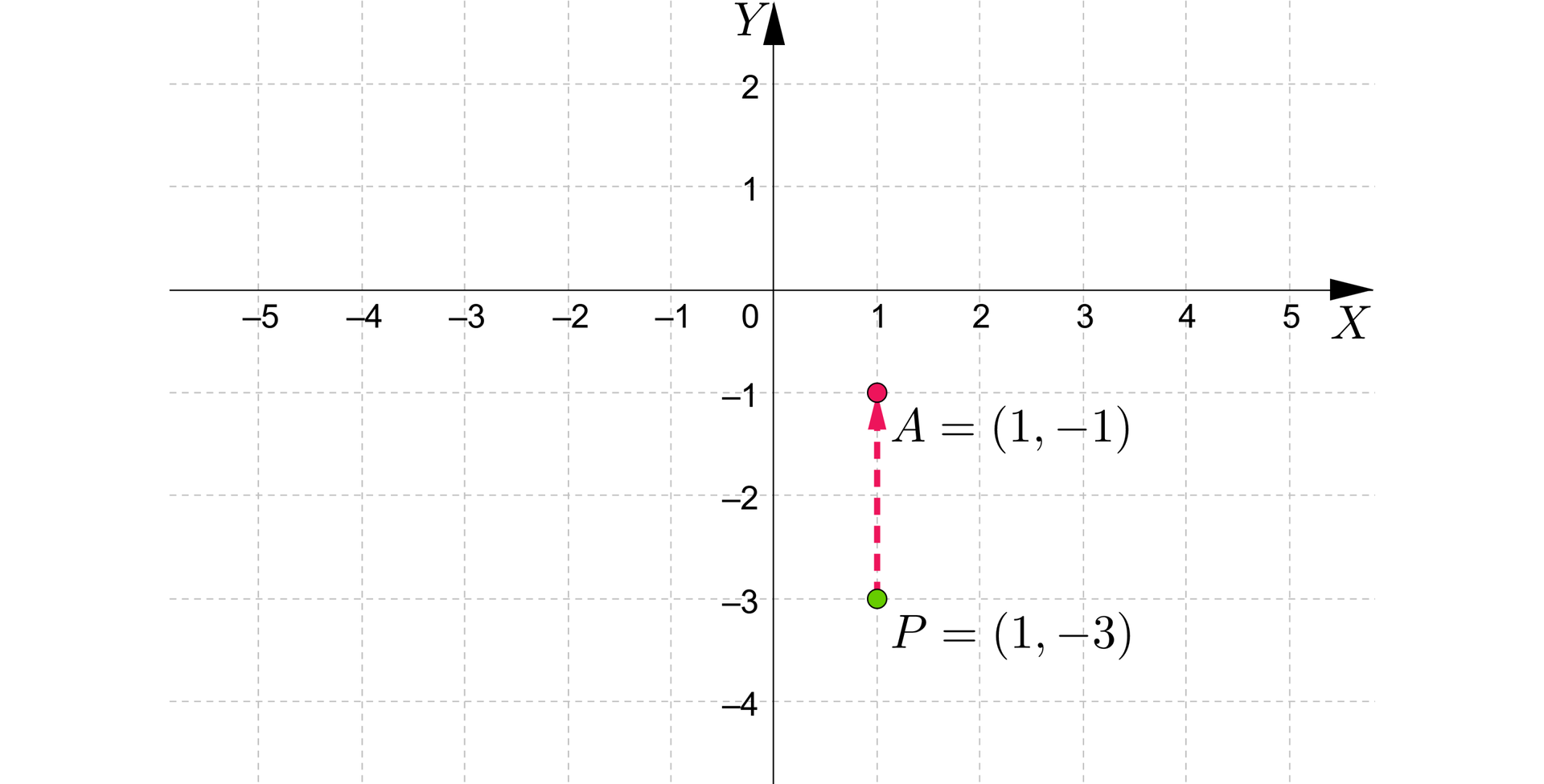
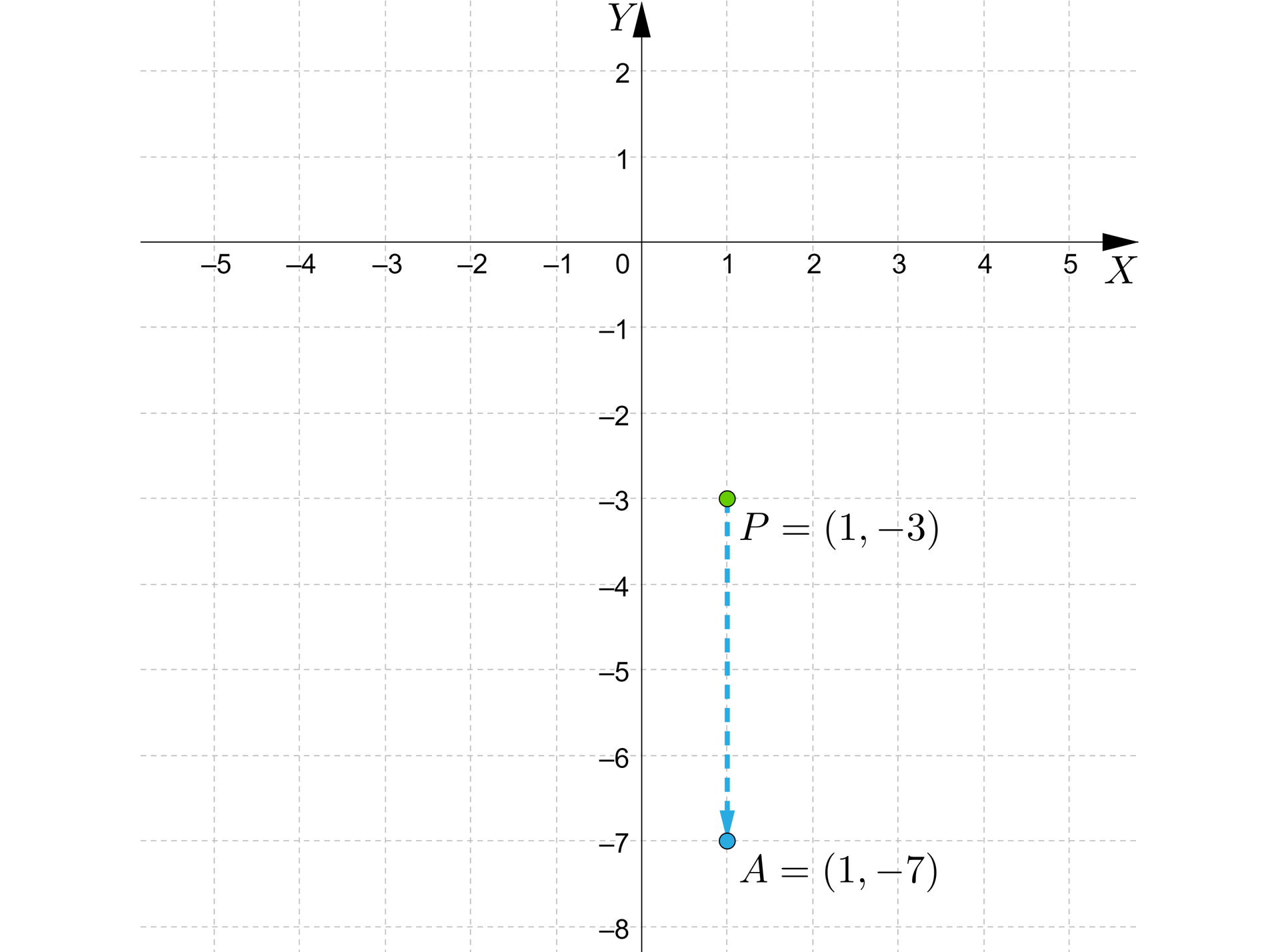
Dany jest punktpunktpunkt $P = (1, - 3)$ . Wyznaczymy współrzędne punktu:

a) $A$ , który otrzymamy w wyniku przesunięcia punktu $P$ o $2$ jednostki w górę wzdłuż osi $Y$ ,

b) $A$ , który otrzymamy w wyniku przesunięcia punktu $P$ o $4$ jednostki w dół wzdłuż osi $Y$ .

Rozwiązanie:

ad a)

W układzie współrzędnych zaznaczamy punkt $P = (1, - 3)$ , a następnie przesuwamy go o dwie jednostki w górę wzdłuż osi $Y$ . Zgodnie z poleceniem, nazywamy go punktem $A$ i odczytujemy jego współrzędne $A = (1, - 1)$ .

R13T1jsAu9Kh7

Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionową oś Y od minus czterech do dwóch. Na układzie współrzędnych zaznaczono punkt P o współrzędnych nawias jeden średnik minus trzy koniec nawiasu oraz punkt A o współrzędnych nawias jeden średnik minus jeden koniec nawiasu.

ad b)

Analogicznie jak w punkcie a) zaznaczamy dany punkt, przesuwamy go zgodnie z poleceniem wzdłuż osi $Y$ . W wyniku przesunięcia danego punktu otrzymujemy punkt $A = (1, - 7)$ .

R6SNLiinkv2nn

Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionową oś Y od minus ośmiu do dwóch. Na układzie współrzędnych zaznaczono punkt P o współrzędnych nawias jeden średnik minus trzy koniec nawiasu oraz punkt A o współrzędnych nawias jeden średnik minus siedem koniec nawiasu.

Zwróćmy uwagę, że w wyniku przesunięcia punktu wzdłuż osi $Y$ , odcięta punktu zostaje bez zmian, natomiast rzędna zmienia się zgodnie z intuicją: przesuwając w górę dodajemy do niej liczbę jednostek, przesuwając w dół odejmujemy liczbę jednostek.

zmiany rzędnej punktu w wyniku przesunięcia wzdłuż osi

Y

Reguła: zmiany rzędnej punktu w wyniku przesunięcia wzdłuż osi

Y

R109GOqnDxRLe

Ilustracja przedstawia punkt A o współrzędnych nawias x średnik y koniec nawiasów oraz punkt A prim przesunięty względem punktu A o cztery jednostki w górę. Punkt ten ma współrzędne nawias x średnik y dodać cztery koniec nawiasu. Pod punktem A znajduje się punkt A bis przesunięty o pięć jednostek w dół. Punkt ten ma współrzędne nawias x średnik y odjąć pięć koniec nawiasu.

Przykład 2

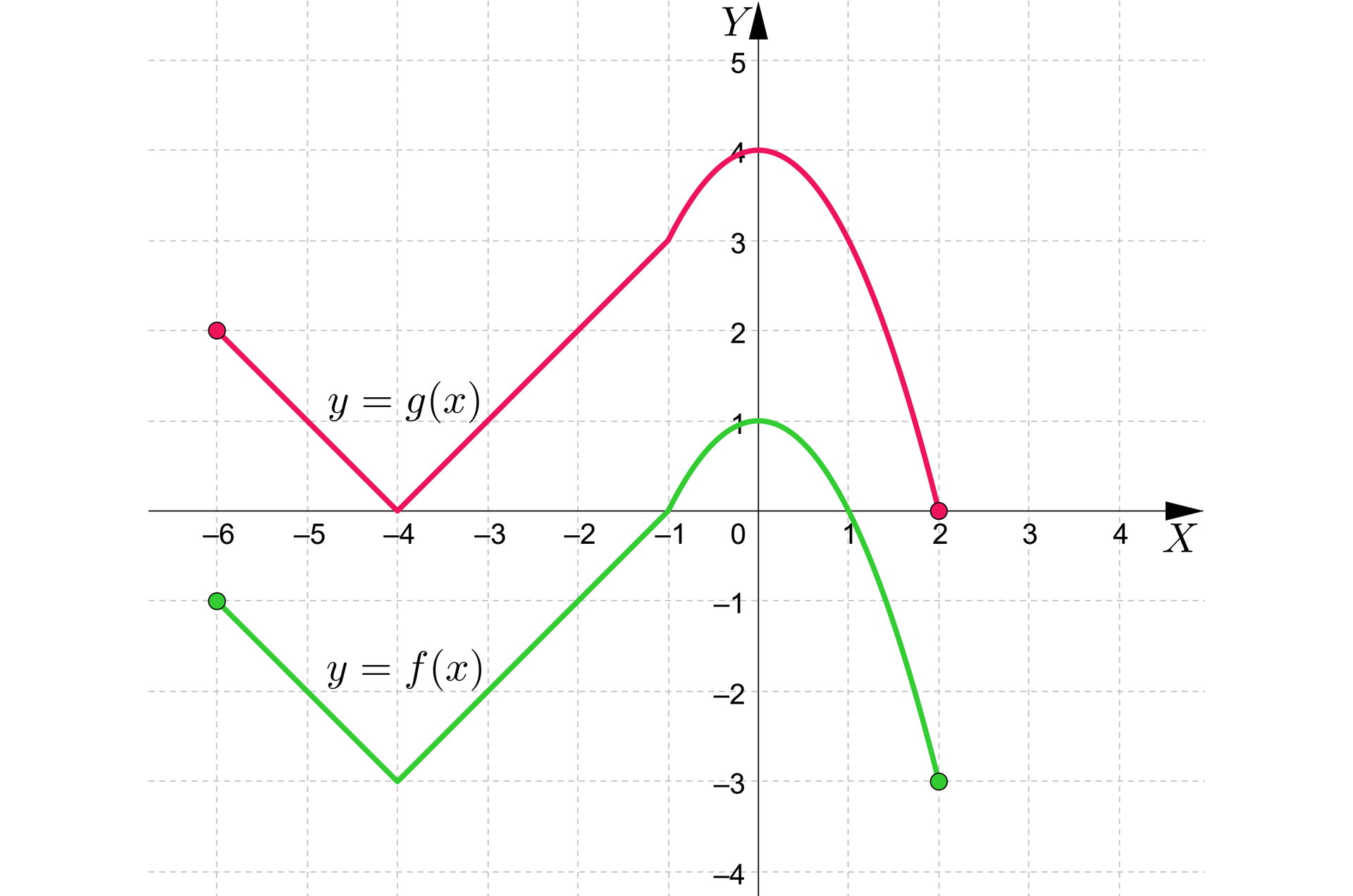
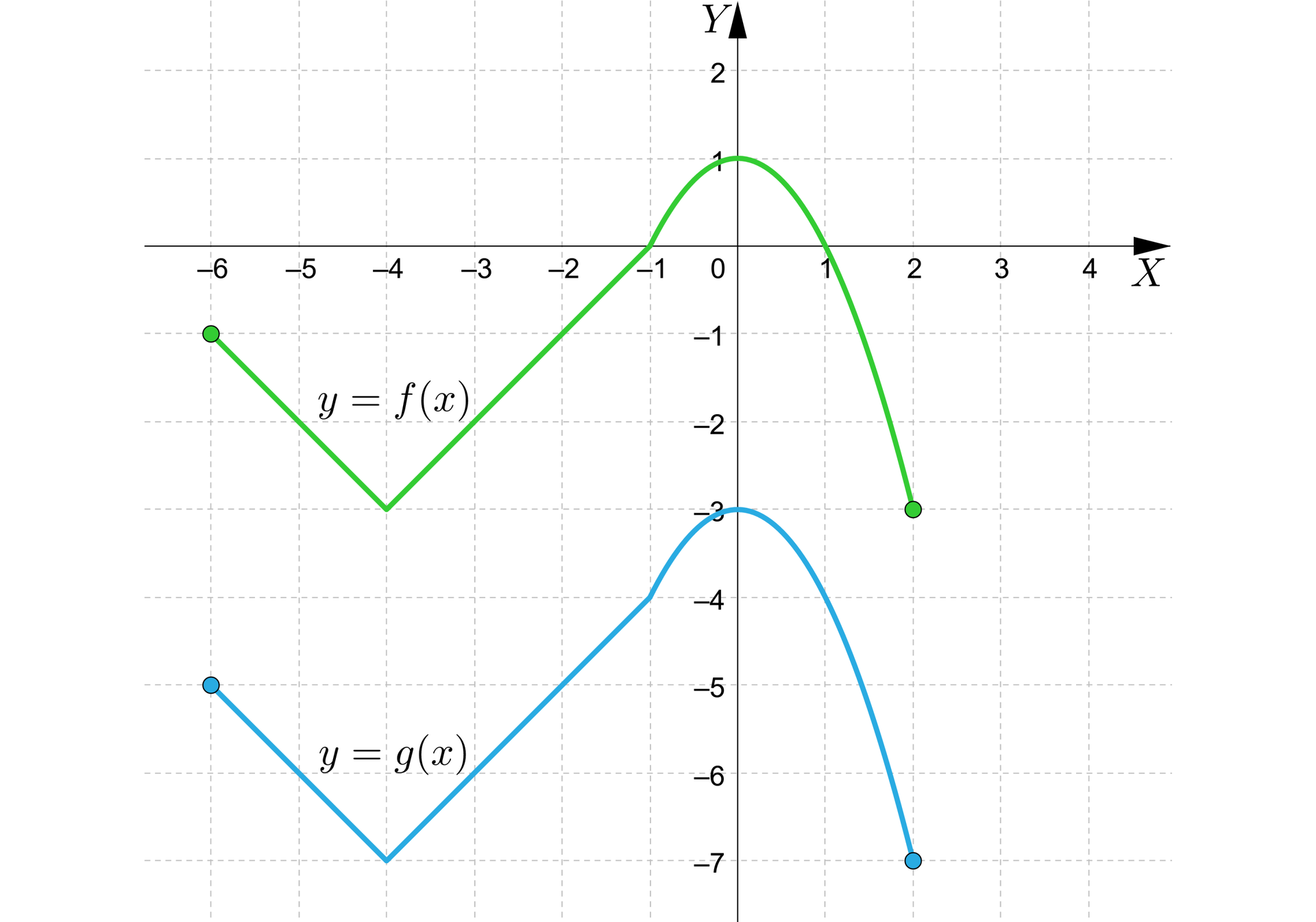
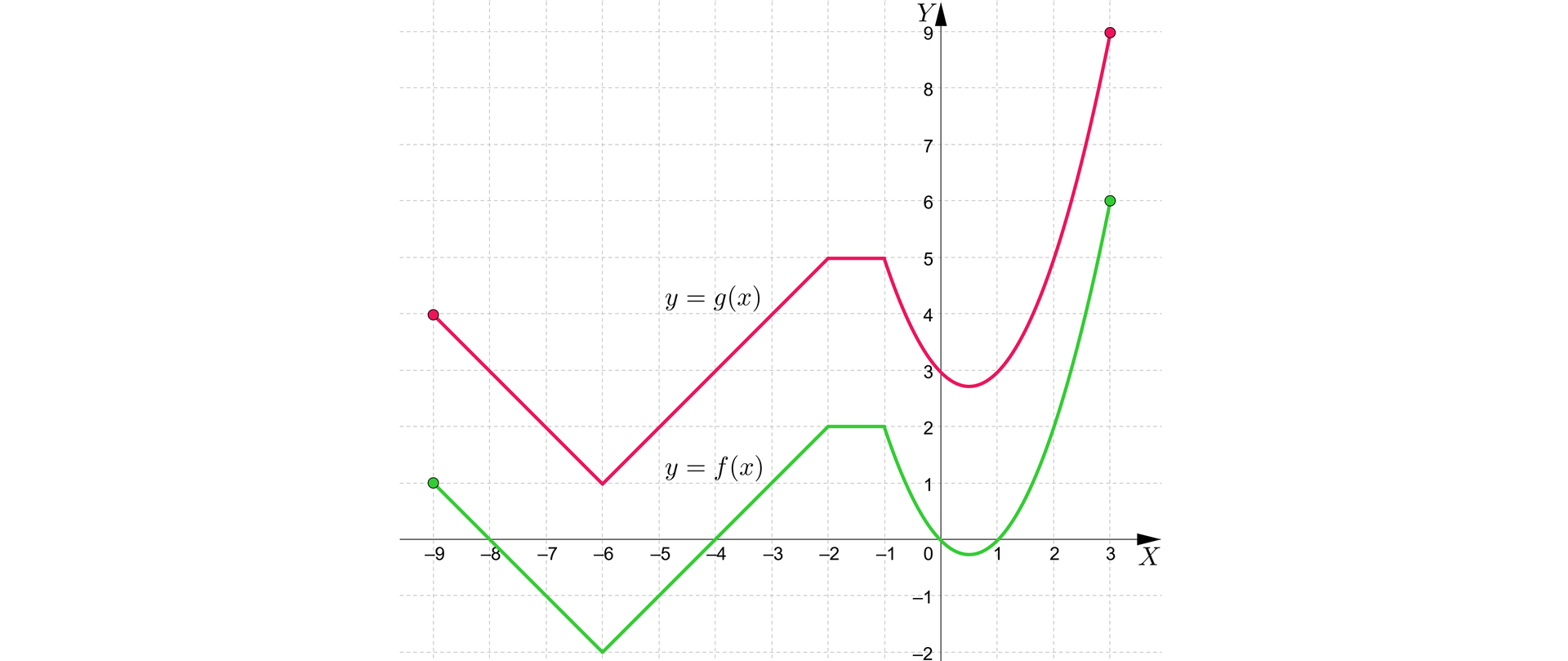
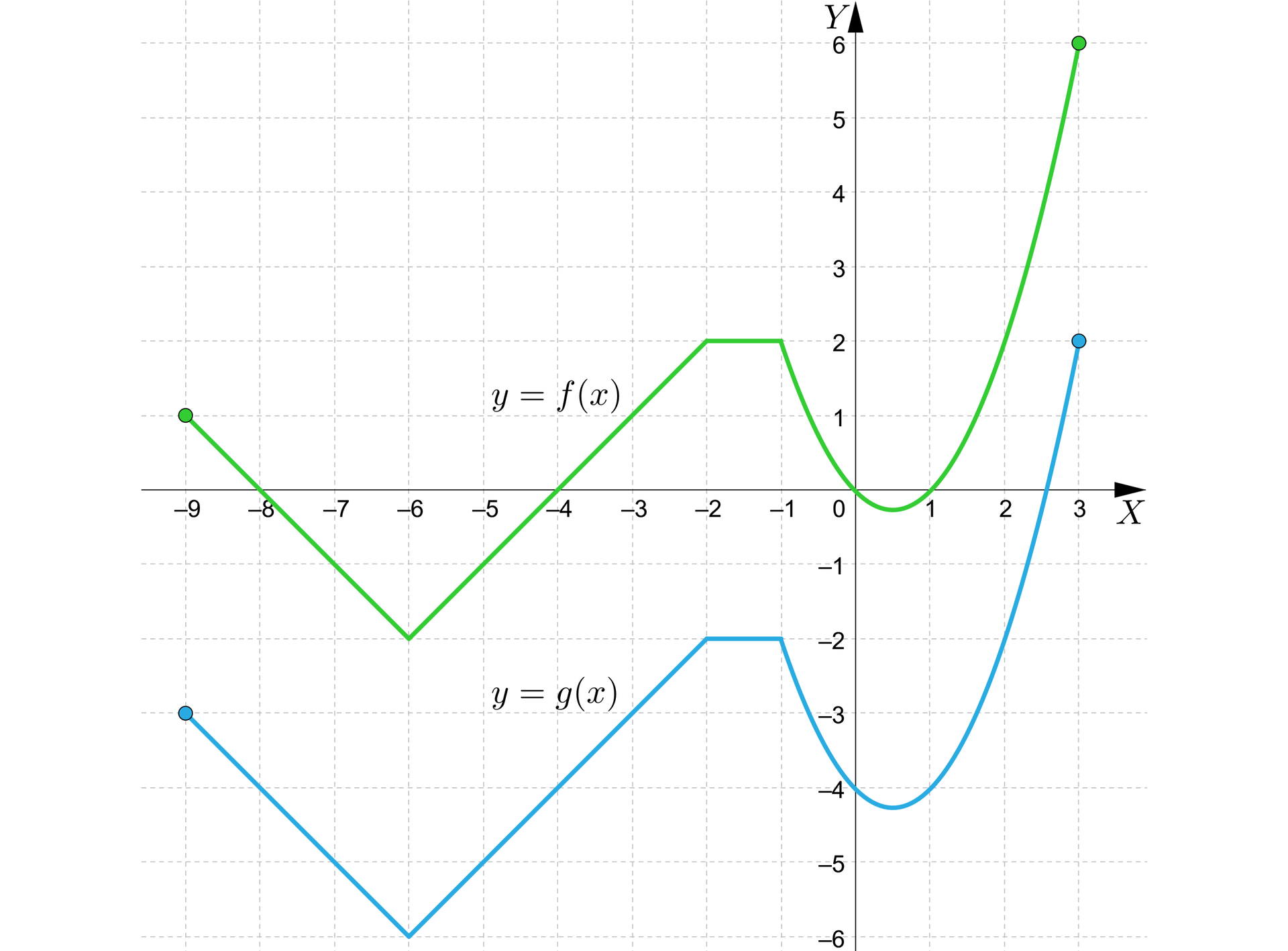
Dany jest wykres funkcji $y = f (x)$ . Sporządzimy wykres funkcji $g (x)$ otrzymany w wyniku przesunięcia danego wykresu:

a) o $3$ jednostki w górę,

b) o $4$ jednostki w dół.

R11mgNpspsHfG

Ilustracja przedstawia poziomą oś X od minus sześciu do czterech oraz pionową oś Y od minus czterech do trzech. Na wykresie zaznaczono wykres funkcji o wzorze y równa się f od x. Wykres ten rozpoczyna się w zamalowanym punkcie nawias minus sześć średnik minus jeden, po czym funkcja maleje do punktu nawias minus cztery średnik minus trzy koniec nawiasu. Następnie funkcja zaczyna rosnąć do punktu nawias minus jeden średnik zero po czym wykres funkcji zamienia się w parabolę o wierzchołku w punkcie nawias zero średnik jeden koniec nawiasu. Następnie wykres paraboli przechodzi przez punkt jeden średnik zero koniec nawiasu, a wykres kończy się w zamalowanym punkcie nawias dwa średnik minus trzy koniec nawiasu.

Rozwiązanie:

Chcąc przesunąć wykres wzdłuż osi $Y$ należy pamiętać o zachowaniu kształtu. W tym celu skupiamy się na charakterystycznych punktachpunktpunktach danego wykresu, które przesuwamy analogicznie, jak w przykładzie pierwszym.

ad a)

wykres funkcji $y = f (x)$ przesuwamy o $3$ jednostki w górę,

RTVsI0ViWKp67

ad b)

wykres funkcji $y = f (x)$ przesuwamy o $4$ jednostki w dół.

RgUbi5H1OLT24

Przykład 3

W kolejnym przykładzie będziemy przesuwać wzdłuż osi $Y$ wykres funkcji $f (x) = |x|, x \in ℝ$ . W przykładzie tym zwróć uwagę na zmianę współrzędnych punktu, który obrazuje przesunięcie punktu wzdłuż osi $Y$ oraz na zmianę wzoru funkcji podczas przesuwania suwakiem w górę lub w dół.

R1Xp6iiew0JEy

Wyprowadzimy zależność między wzorem $y = g (x)$ , a wzorem danej funkcji $y = f (x)$ i liczbą $q$ jednostek, o którą przesuwamy dany wykres wzdłuż osi $Y$ .

R53ysOv9ru7YO

Ilustracja przedstawia punkt P o współrzędnych nawias a średnik b koniec nawiasu oraz punkt P prim przesunięty względem punktu P o q jednostek wzdłuż osi Y o współrzędnych nawias a średnik b dodać q koniec nawiasu.

Zauważmy, że $\{\begin{cases} b = f (a) \\ b + q = g (a) \end{cases} \Rightarrow g (a) = f (a) + q$

Z powyższego wynika, że przy przesuwaniu wykresu funkcji f o $q$ jednostek wzdłuż osi $Y$ , zachodzi zależność $g (x) = f (x) + q$ .

przesuwanie wykresu funkcji wzdłuż osi

Y

Twierdzenie: przesuwanie wykresu funkcji wzdłuż osi

Y

Jeżeli przesuwamy wykres funkcji $y = f (x)$ wzdłuż osi $Y$ o $q$ jednostek, gdzie $q > 0$ , to:

w wyniku przesunięcia w górę otrzymamy wykres funkcji $y = f (x) + q$ ,
w wyniku przesunięcia w dół otrzymamy wykres funkcji $y = f (x) - q$ .

Ważne!

Zwróćmy uwagę, jak zmienia się wzór funkcji otrzymanej w wyniku przesunięcia wzdłuż osi $Y$ :

gdy przesuwamy wykres $y = f (x)$ o $5$ jednostek w górę, wówczas każda wartość funkcji, czyli $f (x)$ , jest powiększona o $5$ , czyli $g (x) = f (x) + 5$ ,
gdy przesuwamy wykres $y = f (x)$ o $3$ jednostki w dół, wówczas każda wartość funkcji, czyli $f (x)$ , jest pomniejszona o $3$ , czyli $g (x) = f (x) - 3$ .

R19WEaiEMEdYn

Ilustracja przedstawia wzór funkcji o równaniu y równa się f od x. Poniżej równania znajduje się strzałka prowadząca do wzoru funkcji przesuniętej o trzy jednostki w dół o równaniu y równa się f od x odjąć trzy. Nad pierwotnym wzorem funkcji znajduje się strzałka wskazująca w górę prowadząca do wzoru funkcji przesuniętej o pięć jednostek w górę o równaniu y równa się f od x dodać pięć.

Przykład 4

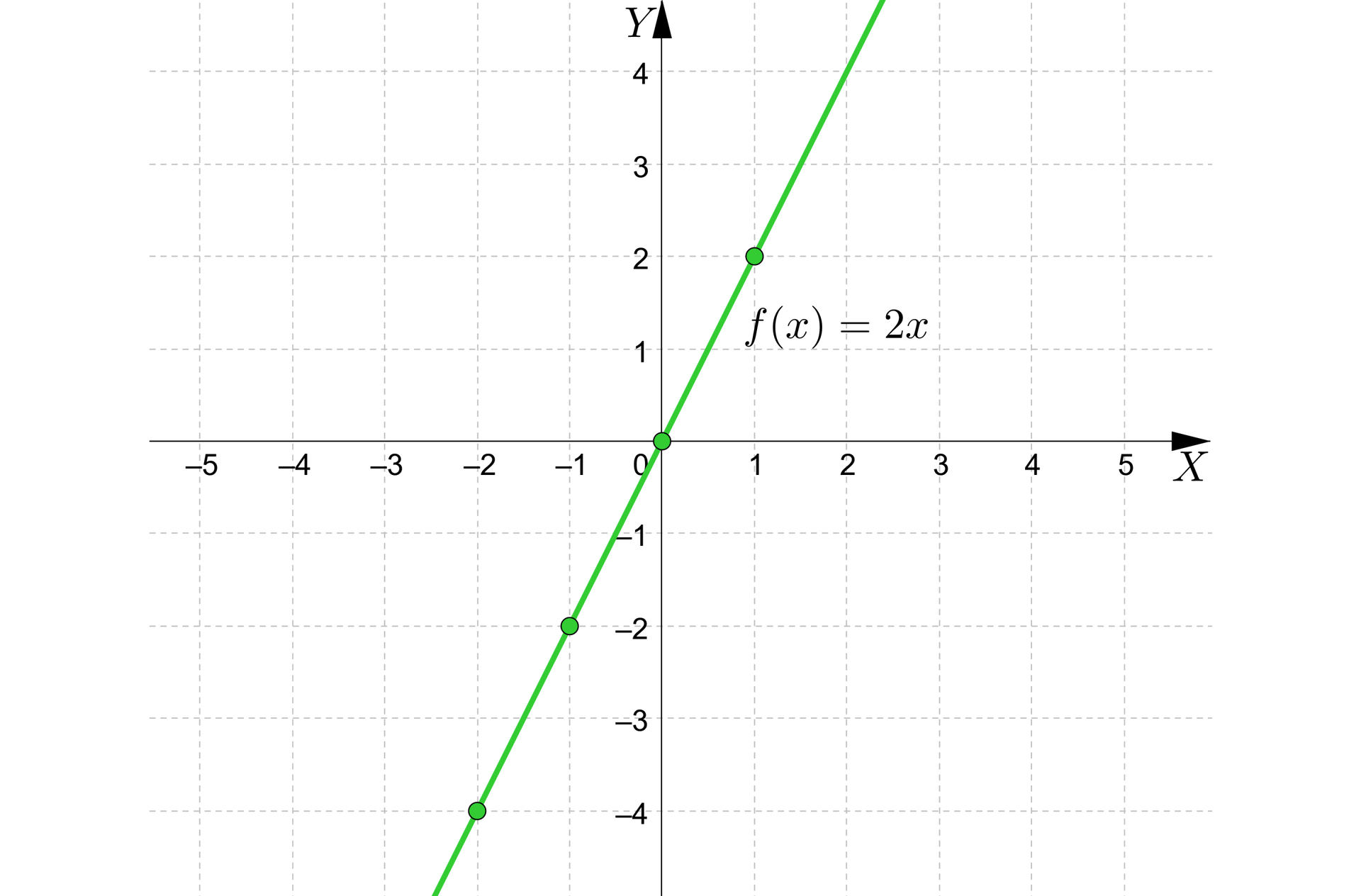
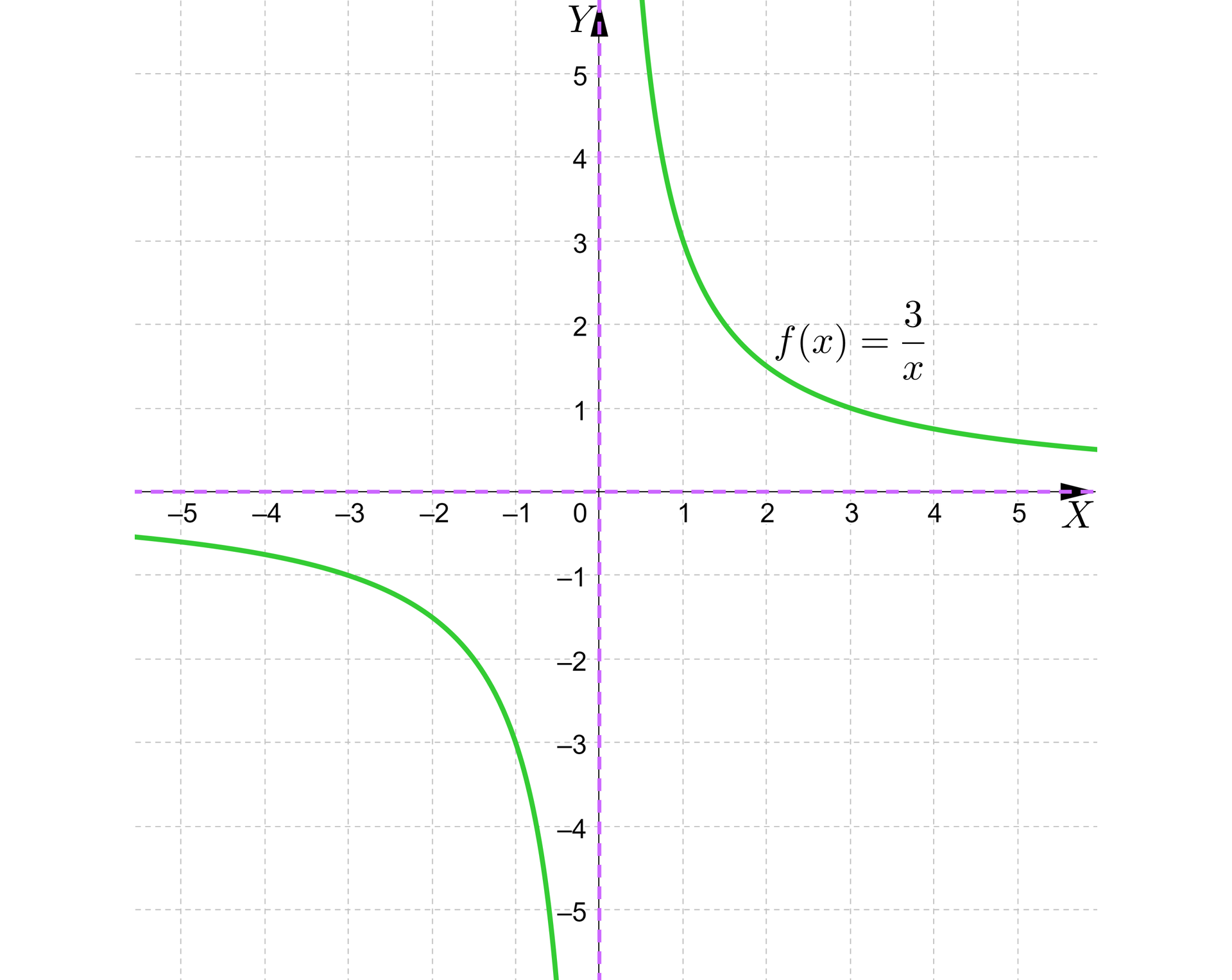
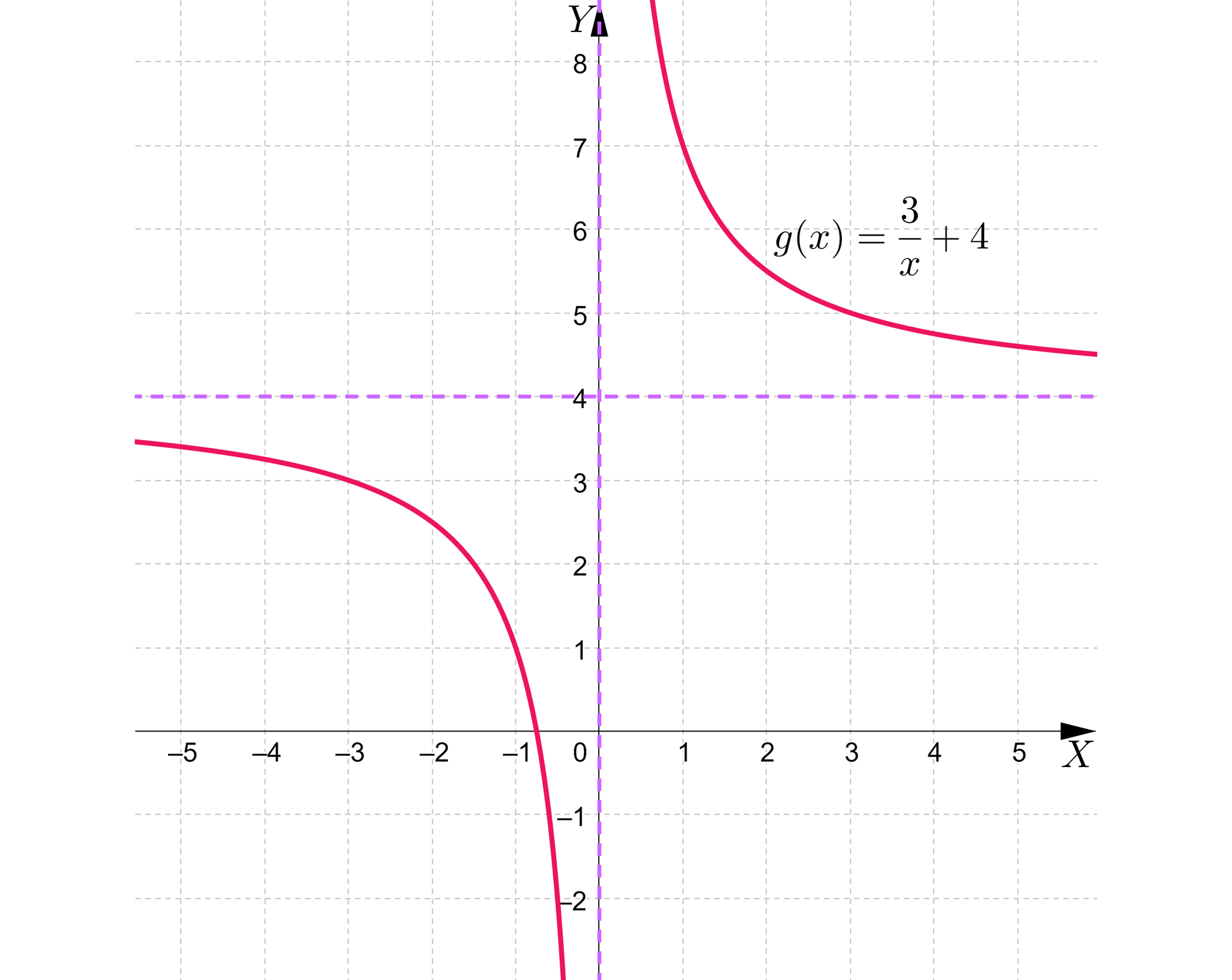
Dany jest wykres funkcji $y = f (x)$ . Przesuniemy wykres funkcji $y = f (x)$ mając wzór funkcji $g (x)$ oraz wypiszemy dla każdej z tych funkcji: dziedzinę funkcji, zbiór wartościzbiór wartości funkcjizbiór wartości, wartość najmniejszą, wartość największą oraz punkt przecięcia wykresu funkcji z osią $Y$ punkt przecięcia wykresu funkcji z osią $Y$ .

RA0J6WouYrlJ0

Ilustracja przedstawia poziomą oś X od minus dziewięciu do trzech oraz pionową oś Y od minus dwóch do sześciu. Na wykresie zaznaczono wykres funkcji y równa się f od x rozpoczynający się w zamalowanym punkcie nawias minus dziewięć średnik jeden. Wykres maleje do punktu nawias minus sześć średnik minus dwa koniec nawiasu po czym zaczyna rosnąć do punktu nawias minus dwa średnik dwa. Następnie do punktu nawias minus jeden średnik dwa funkcja jest stała. Po osiągnięciu tego punktu funkcja zamienia się w wykres paraboli o wierzchołku w punkcie nawias zero przecinek pięć średnik minus zero przecinek dwadzieścia pięć koniec nawiasu i miejscach zerowych w punktach nawias zero średnik zero koniec nawiasu i nawias jeden średnik zero koniec nawiasu. Wykres funkcji kończy się w punkcie nawias trzy średnik sześć koniec nawiasu.

Sporządzimy wykres funkcji:

a) $g (x) = f (x) + 3$ ,

b) $g (x) = f (x) - 4$ .

Rozwiązanie:

ad a)

Rozwiązanie rozpoczynamy od analizy wzoru $g (x) = f (x) + 3$ . Wzór funkcji $g (x)$ oznacza, że każda wartość danej funkcji f jest powiększona o $3$ , co oznacza, że wykres funkcji f przesunięto w górę o $3$ jednostki wzdłuż osi $Y$ .

Rqtpcsx8KRvAL

Ilustracja przedstawia poziomą oś X od minus dziewięciu do trzech oraz pionową oś Y od minus dwóch do dziewięciu . Na wykresie zaznaczono wykres funkcji y równa się f od x rozpoczynający się w zamalowanym punkcie nawias minus dziewięć średnik jeden. Wykres maleje do punktu nawias minus sześć średnik minus dwa koniec nawiasu po czym zaczyna rosnąć do punktu nawias minus dwa średnik dwa. Następnie do punktu nawias minus jeden średnik dwa funkcja jest stała. Po osiągnięciu tego punktu funkcja zamienia się w wykres paraboli o wierzchołku w punkcie nawias zero przecinek pięć średnik minus zero przecinek dwadzieścia pięć koniec nawiasu i miejscach zerowych w punktach nawias zero średnik zero koniec nawiasu i nawias jeden średnik zero koniec nawiasu. Wykres funkcji kończy się w punkcie nawias trzy średnik sześć koniec nawiasu. Nad wykresem funkcji f od x znajduje się wykres funkcji g od x. Wykres ten jest taki sam jak wykres funkcji pierwszej przesuniętej o trzy jednostki do góry. Przykładowo funkcja g od x rozpoczyna się w punkcie nawias minus dziewięć średnik cztery koniec nawiasu, a kończy się w punkcie nawias trzy średnik dziewięć koniec nawiasu.

Własności funkcji zestawimy w tabelce:

Funkcja	Dziedzina	Zbiór wartości	Najmniejsza wartość	Największa wartość	Punkt przecięcia z osią $Y$
$y = f (x)$	$D_{f} = ⟨- 9, 3⟩$	$Z W_{f} = ⟨- 2, 6⟩$	$f_{m i n} = - 2$	$f_{m a x} = 6$	$(0, 0)$
$g (x) = f (x) + 3$	$D_{g} = ⟨- 9, 3⟩$	$Z W_{g} = ⟨1, 9⟩$	$g_{m i n} = 1$	$g_{m a x} = 9$	$(0, 3)$

ad b)

Wzór funkcji $g (x) = f (x) - 4$ oznacza, że każda wartość danej funkcji f jest pomniejszona o $4$ , co oznacza, że wykres danej funkcji przesunięto w dół o $4$ jednostki wzdłuż osi $Y$ .

RJJ8f9SIpalIy

Ilustracja przedstawia poziomą oś X od minus dziewięciu do trzech oraz pionową oś Y od minus sześciu do sześciu . Na wykresie zaznaczono wykres funkcji y równa się f od x rozpoczynający się w zamalowanym punkcie nawias minus dziewięć średnik jeden. Wykres maleje do punktu nawias minus sześć średnik minus dwa koniec nawiasu po czym zaczyna rosnąć do punktu nawias minus dwa średnik dwa. Następnie do punktu nawias minus jeden średnik dwa funkcja jest stała. Po osiągnięciu tego punktu funkcja zamienia się w wykres paraboli o wierzchołku w punkcie nawias zero przecinek pięć średnik minus zero przecinek dwadzieścia pięć koniec nawiasu i miejscach zerowych w punktach nawias zero średnik zero koniec nawiasu i nawias jeden średnik zero koniec nawiasu. Wykres funkcji kończy się w punkcie nawias trzy średnik sześć koniec nawiasu. Pod wykresem funkcji f od x znajduje się wykres funkcji g od x. Wykres ten jest taki sam jak wykres funkcji pierwszej przesuniętej o cztery jednostki w dół. Przykładowo funkcja g od x rozpoczyna się w punkcie nawias minus dziewięć średnik minus trzy koniec nawiasu, a kończy się w punkcie nawias trzy średnik dwa koniec nawiasu.

Własności funkcji zestawimy w tabelce:

Funkcja	Dziedzina	Zbiór wartości	Najmniejsza wartość	Największa wartość	Punkt przecięcia z osią $Y$
$y = f (x)$	$D_{f} = ⟨- 9, 3⟩$	$Z W_{f} = ⟨- 2, 6⟩$	$f_{m i n} = - 2$	$f_{m a x} = 6$	$(0, 0)$
$g (x) = f (x) - 4$	$D_{g} = ⟨- 9, 3⟩$	$Z W_{g} = ⟨- 6, 2⟩$	$g_{m i n} = - 6$	$g_{m a x} = 2$	$(0, - 4)$

Przykład 5

Sporządzimy wykres funkcji $f (x) = 2 x$ . W tym celu sporządzimy tabelę częściową z wartościami funkcji:

$x$	$- 2$	$- 1$	$0$	$1$
$f (x) = 2 x$	$- 4$	$- 2$	$0$	$2$

Mając tabelę zaznaczymy otrzymane punkty w układzie współrzędnych i wykreślimy prostą. Pamiętamy, że przez dwa punkty na płaszczyźnie przechodzi dokładnie jedna prosta. Oznacza to, że wystarczy wyznaczyć współrzędne dwóch punktów, by sporządzić wykres funkcji liniowej.

R1VJrINV57YH9

Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionową oś Y od minus czterech do czterech. Na wykresie zaznaczono wykres funkcji f od x równa się dwa x. Funkcja ta jest prostą przechodzącą przez punkty nawias minus dwa średnik minus cztery koniec nawiasu, nawias minus jeden średnik minus dwa koniec nawiasu , nawias zero średnik zero koniec nawiasu, nawias jeden średnik dwa koniec nawiasu.

Korzystając z umiejetności przesuwania wykresu funkcji wzdłuż osi $Y$ sporządzimy wykres funkcji $g (x) = 2 x + 5$ . Zauważmy, że wartości funkcji $g$ są o $5$ większe od wartości funkcji $f$ , zatem każdy punkt wykresu funkcji $f$ należy przesunąć o $5$ jednostek w górę.

R1L2nJvEPzHh3

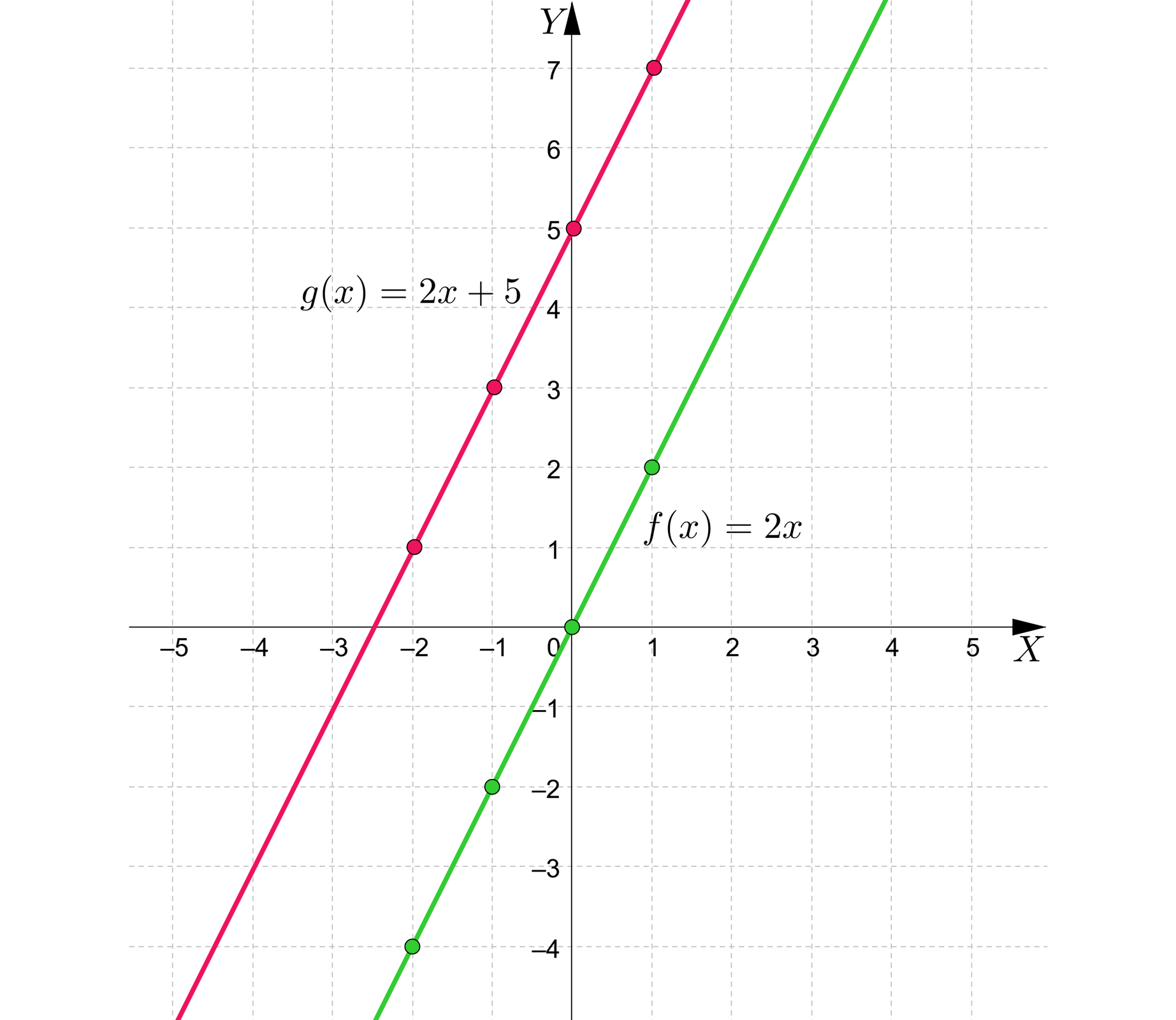
Zwróćmy uwagę na współrzędne punktu przecięcia wykresów funkcji z osią $Y$ .

Wykres funcji $f (x) = 2 x$ przecina oś $Y$ w punkcie $(0, 0)$ , zaś wykres funkcji $g (x) = 2 x + 5$ w punkcie $(0, 5)$ .

Ważne!

Przesunięcie wykresu funkcji $y = f (x)$ wzdłuż osi $Y$ ma wpływ na:

zbiór wartości funkcjizbiór wartości funkcjizbiór wartości funkcji $g (x)$ , której wykres otrzymano,
najmniejszą, największą wartość funkcji $g (x)$ (o ile istnieją),
rzędną punktu przecięcia wykresu funkcji z osią $Y$ punktu przecięcia wykresu funkcji z osią $Y$ .

Dla zainteresowanych

Przesuwając hiperbolę $y = \frac{a}{x}$ , gdzie $a \in ℝ ∖ \{0\}$ , $x \in ℝ ∖ \{0\}$ , wzdłuż osi $Y$ należy pamiętać, aby przesunąć w tym samym kierunku i o tyle samo jednostek asymptotę poziomą wykresu funkcji.

R1AUX4H0TSD6c

Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionową oś Y od minus pięciu do pięciu. Na rysunku zaznaczono wykres funkcji homograficznej f od x równa się trzy przez x. Wykres tej funkcji ma dwie asymptoty zawarte w poziomej osi X i pionowej osi Y. Funkcja ta jest malejąca i przechodzi przez charakterystyczne punkty nawias minus trzy średnik minus jeden koniec nawiasu, nawias minus jeden średnik minus trzy koniec nawiasu, nawias jeden średnik trzy koniec nawiasu, nawias trzy średnik jeden koniec nawiasu.

R15LwGZftTxSj

Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu oraz pionową oś Y od minus dwóch do ośmiu. Na rysunku zaznaczono wykres funkcji homograficznej g od x równa się trzy przez x dodać cztery. Wykres tej funkcji ma dwie asymptoty pierwsza pionowa zawarta w osi Y i drugą poziomą o równaniu y równa się cztery. Funkcja ta jest malejąca i przechodzi przez charakterystyczne punkty nawias minus trzy średnik trzy koniec nawiasu, nawias minus jeden średnik jeden koniec nawiasu, nawias jeden średnik siedem koniec nawiasu, nawias trzy średnik pięć koniec nawiasu.

Słownik

punkt

w układzie współrzędnych uporządkowana para liczb $(x, y)$ ; pierwsza liczba to pierwsza współrzędna punktu nazywamy odciętą, zaś druga to rzędna punktu

zbiór wartości funkcji

zbiór tych wszystkich liczb $y$ , dla których istnieje taki argument $x \in D$ , że $f (x) = y$ ; mając dany wykres funkcji, zbiór wartości odczytujemy z osi $Y$

punkt przecięcia wykresu funkcji z osią

Y

punkt przecięcia wykresu funkcji z osią

Y

punkt, którego odciętą jest $0$ , zaś rzędną jest wartość funkcji dla argumentu $0$ , czyli jest to punkt o współrzędnych $(0, f (0))$

Wprowadzenie

Schemat interaktywny

Słownik