Przeczytaj

Trójkąt opisany na okręgu

Definicja: Trójkąt opisany na okręgu

Trójkąt opisany na okręgu, jest to trójkąt, którego wszystkie boki są styczne do danego okręgu.

Trójkąt jest opisany na okręgu wtedy i tylko wtedy, gdy ten okrąg jest wpisany w ten trójkąt.

W przypadku okręgu wpisanego w trójkąt, zwykle dany jest trójkąt i trzeba wpisać weń okrąg. Dla każdego trójkąta istnieje dokładnie jeden okrąg wpisany.

Natomiast w przypadku trójkąta opisanego, zwykle to okrąg jest dany i trzeba zbudować trójkąt tak, żeby ten okrąg był wpisany w trójkąt. Okazuje się, że na danym okręgu można opisać nieskończenie wiele trójkątów, a dokładniej dowolny trójkąt z dokładnością do podobieństwapodobieństwo figurpodobieństwa.

Twierdzenie o trójkącie opisanym na okręgu

Twierdzenie: Twierdzenie o trójkącie opisanym na okręgu

Dany jest okrąg o środku $O$ i promieniu $r$ oraz trójkąt $A' B' C'$ . Wówczas na tym okręgu możemy opisać trójkąt $A B C$ podobny do trójkąta $A' B' C'$ .

Dowód

Opiszemy jak skonstruować trójkąt $A B C$ podobny do trójkąta $A' B' C'$ .

Zaczynamy od skonstruowania okręgu wpisanego w trójkąt $A' B' C'$ i przyjmijmy że promień tego okręgu wynosi $r'$ .

Wówczas okrąg jest podobny do danego okręgu w skali $k = \frac{r'}{r}$ . Przekształcamy figurę będącą trójkątem z wpisanym okręgiem na figurę podobną w skali $k_{1} = \frac{r}{r'}$ .

Nazywamy wierzchołki skonstruowanego trójkąta (odpowiednio) $A$ , $B$ , $C$ .

Przykład 1

Okrąg wpisany w trójkąt egipski (trójkąt o bokach $3$ , $4$ , $5$ ) ma promień równy $1$ . Wyznaczymy długości boków trójkąta podobnegocechy podobieństwa trójkątówtrójkąta podobnego do trójkąta egipskiego opisanego na okręgu o promieniu $r$ .

Z powyższego twierdzenia skala podobieństwa wynosi $k = \frac{r}{1} = r$ . Stąd trójkąt podobny do trójkąta egipskiego opisany na okręgu o promieniu $r$ ma boki długości $3 r$ , $4 r$ , $5 r$ .

Prosta styczna do okręgu to prosta, która ma dokładnie jeden punkt wspólny z okręgiem.

Własności prostych stycznych do okręgu

Własność: Własności prostych stycznych do okręgu

Rd5W8MpU6uMVD

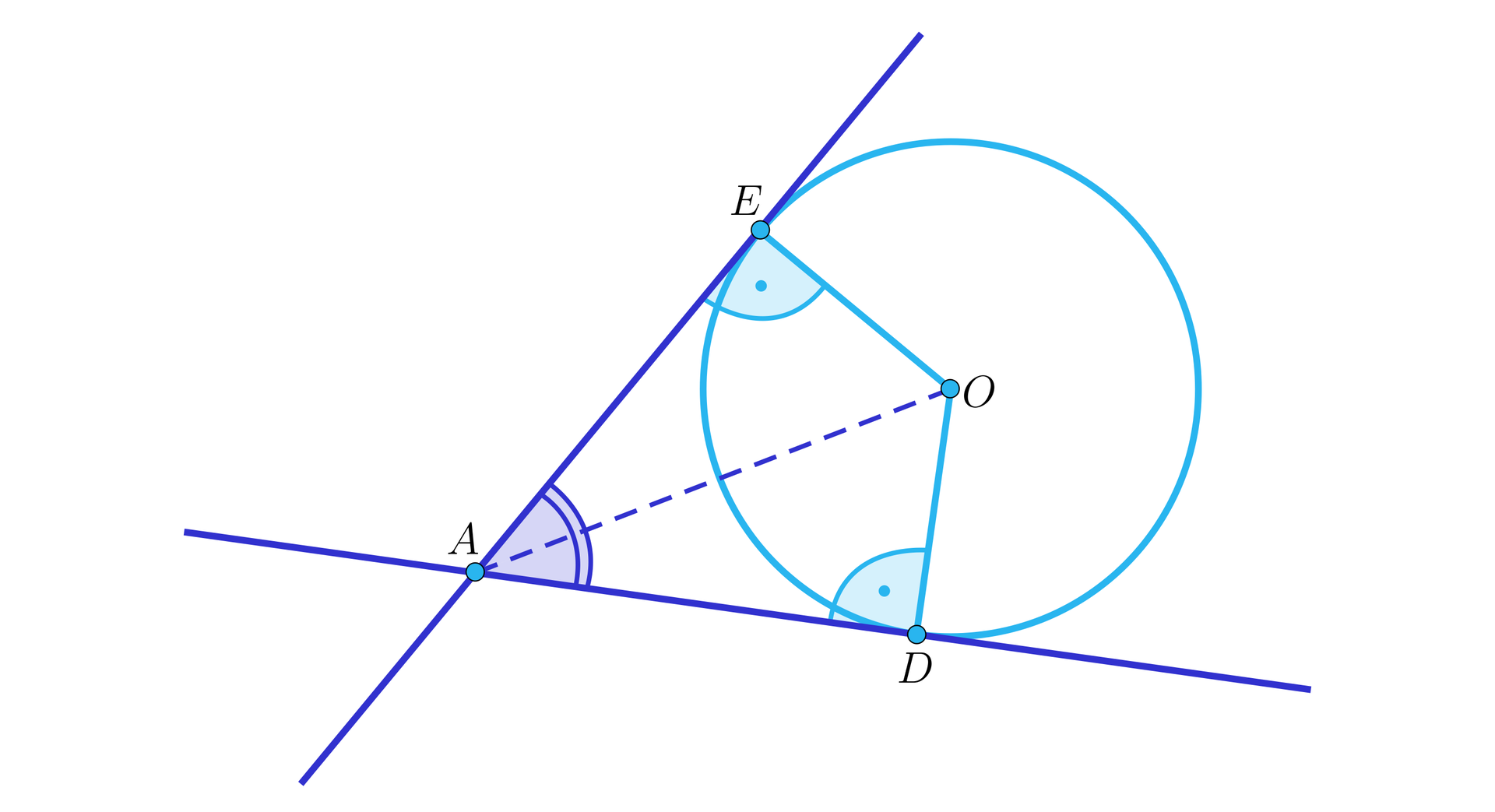
Grafika przedstawia okrąg o środku O oraz styczne do tego okręgu przecinające się w punkcie A. Styczne stykają się z okręgiem w punktach E i D. Promienie okręgu tworzą odcinki OE i OD. Zaznaczone są również kąty proste AEO i ADO oraz zaznaczony na niebiesko jest kąt EAD. Od punktu przecięcia stycznych A do środka okręgu O poprowadzona jest przerywana linia.

Z dowolnego punktu $A$ leżącego na zewnątrz okręgu można poprowadzić dokładnie dwie proste styczne do okręgu.
Promień okręgu poprowadzony do punktu styczności z prostą styczną jest prostopadły do tej prostej.
Jeśli z punktu $A$ leżącego na zewnątrz okręgu poprowadzimy proste styczne do okręgu w punktach $D$ i $E$ , to trójkąty $A O D$ i $A O E$ są przystającymi trójkątami prostokątnymi. Stąd odcinki $A D$ i $A E$ mają równe długości. Odcinki te nazywamy odcinkami stycznymi. Natomiast półprosta $A O$ jest dwusieczną kąta $D A E$ .

Własność odcinków stycznych w trójkącie opisanym na okręgu

Własność: Własność odcinków stycznych w trójkącie opisanym na okręgu

RojF3CNHtd2wN

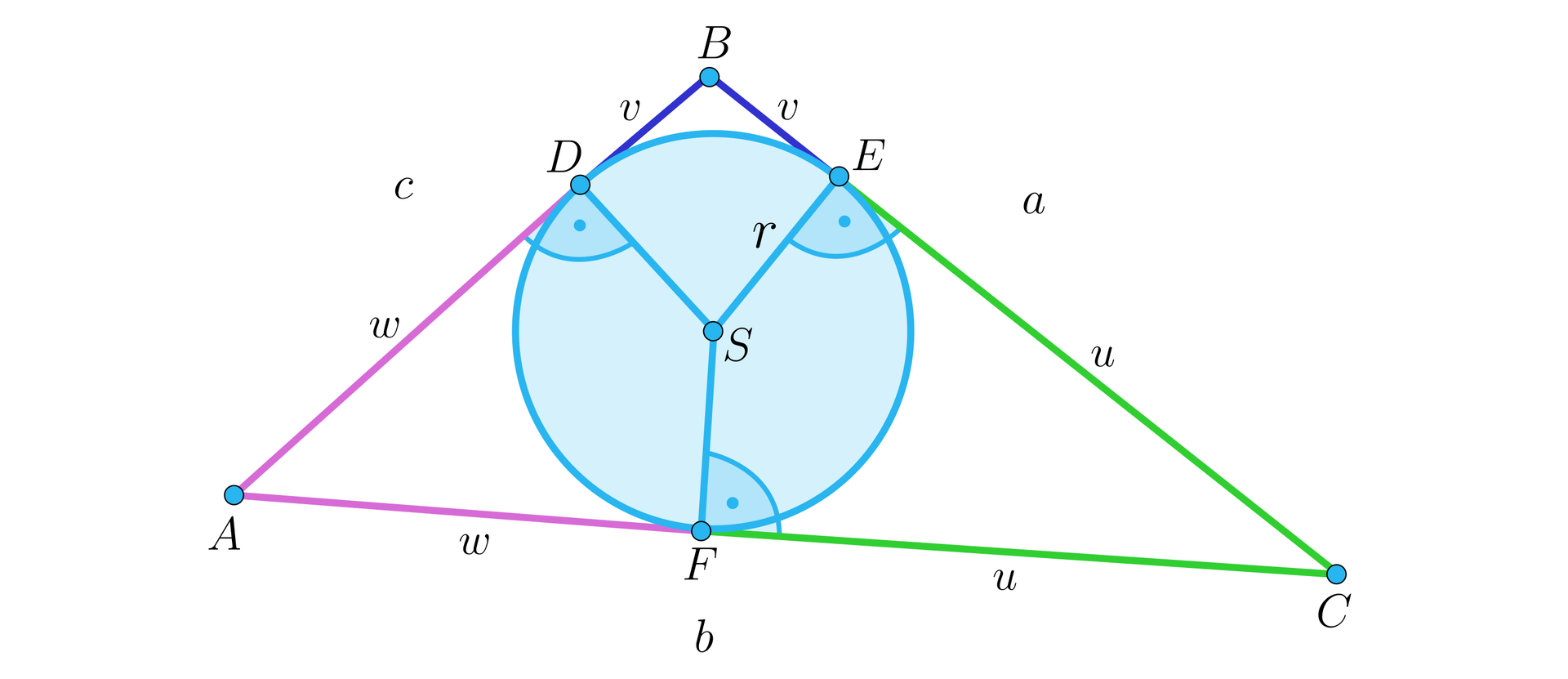
Ilustracja przedstawia trójkąt ABC w który wpisany jest niebieski okrąg o środku S. Promienie okręgu o długości r w punktach styku dzielą boki trójkąta na odcinki. Bok AB o długości c jest podzielony na odcinki AD i DB , bok BC o długości a jest podzielony na odcinki BE i EC a bok AC o długości b jest podzielony na odcinki AF i FC. Zielone odcinki FC i EC mają długość u , niebieskie odcinki DB i BE mają długość v a różowe odcinki AD i AF mają długość w.

Niech $D$ , $E$ , $F$ będą punktami styczności okręgu z bokami trójkąta. Wtedy przy oznaczeniach z rysunku:

$|C E| = |C F| = u = \frac{a + b - c}{2}$ ,

$|B D| = |B E| = v = \frac{a + c - b}{2}$ ,

$|A D| = |A F| = w = \frac{b + c - a}{2}$

Przykład 2

Mamy zakupić narożną szafkę w kształcie graniastosłupa, którego podstawą jest trójkąt prostokątny taki, że stosunek długości przyprostokątnych jest $3:4$ . Wyznaczymy minimalne rozmiary podstawy tej szafki tak, żeby zmieściły się w niej okrągłe półmiski o średnicy $40 cm$ .

RgEpkp4ujlPQJ

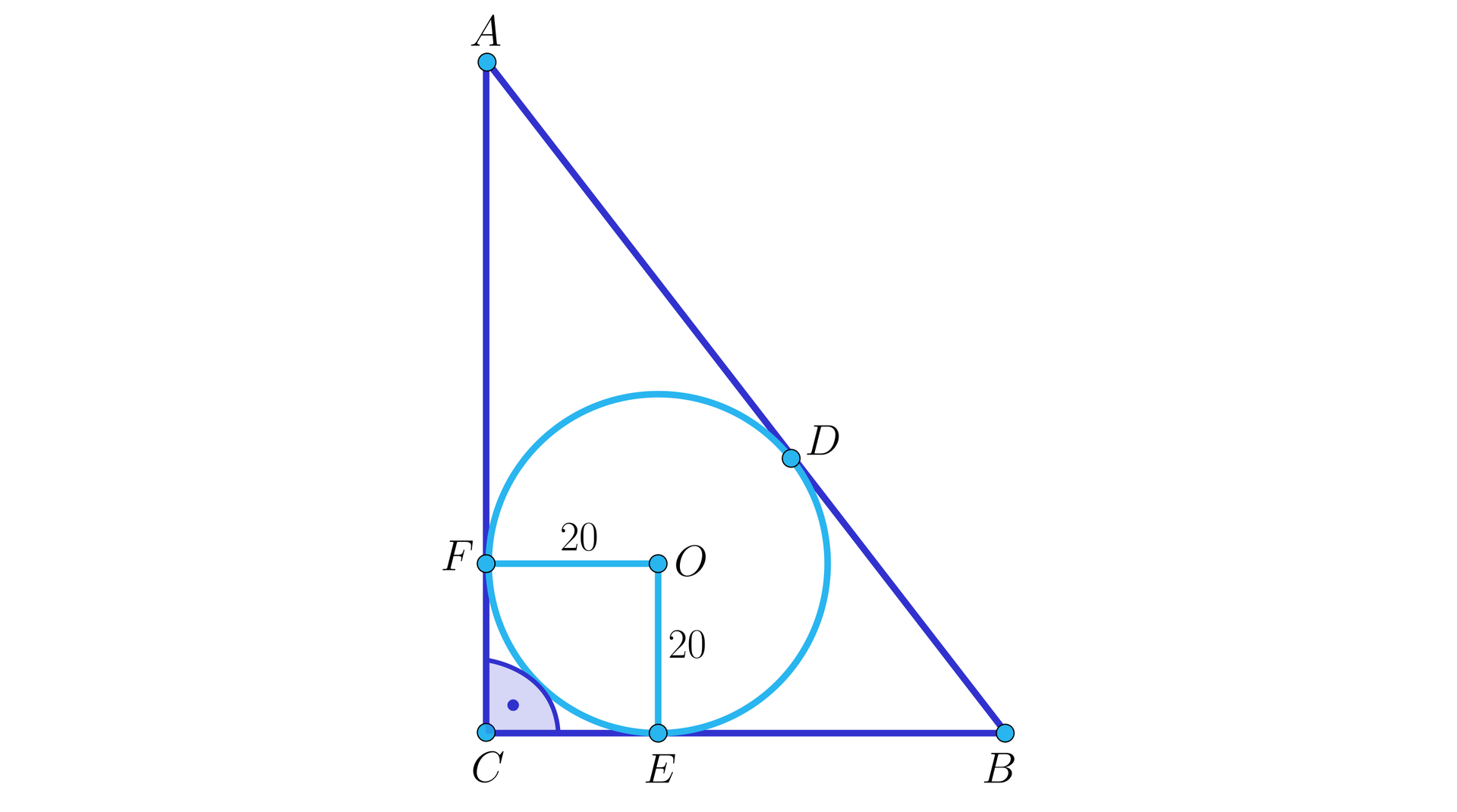
Ilustracja przedstawia trójkąt prostokątny ABC z kątem prostym ACB, w który wpisany jest okrąg o środku O . Okrąg styka się z trójkątem w punkcie D na boku AB , tworząc odcinki AD i DB , w punkcie E na boku CB tworząc odcinki CE i EB oraz w punkcie F na boku AC tworząc odcinki AF i FC . Promienie okręgu tworzą odcinki OE i OF o długości 20. Punkty OECF tworzą kwadrat.

Ponieważ stosunek długości przyprostokątnych jest $3:4$ , to niech $|C B| = 3 x$ , $|C A| = 4 x$ . Wtedy $|A B| = 5 x$ .

Korzystając z własności odcinków stycznych dostajemy

$5 x = 3 x - 20 + 4 x - 20 = 7 x - 40$

$2 x = 40$

$x = 20$

Ostatecznie, wymiary szafki wynoszą $60 cm$ , $80 cm$ , $100 cm$ .

Długość promienia okręgu wpisanego w trójkąt

Twierdzenie: Długość promienia okręgu wpisanego w trójkąt

Promień okręgu wpisanego w trójkąt o bokach $a$ , $b$ , $c$ i polu $P$ wynosi $r = \frac{2 P}{a + b + c}$ .

Przykład 3

Wyznaczymy długości boków trójkąta opisanego na okręgu o promieniu $r = 10$ , jeżeli wiadomo, że stosunek boków tego trójkąta wynosi $7:9:12$ .

Wyznaczamy promień okręgu wpisanego w trójkąt o bokach $7$ , $9$ , $12$ . Promień tego okręgu wyznaczymy ze wzoru wynosi $r' = \frac{2 P}{a + b + c}$ .

Pole wyznaczamy ze wzoru Herona $P = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{14 \cdot 7 \cdot 5 \cdot 2} = 14 \sqrt{5}$ .

Stąd $r' = \frac{2 \cdot 14 \sqrt{5}}{28} = \sqrt{5}$ .

Wyznaczamy skalę podobieństwa $k = \frac{r}{r'} = \frac{10}{\sqrt{5}} = 2 \sqrt{5}$ .

Ostatecznie, trójkąt opisany na okręgu o promieniu $r = 10$ , którego stosunek boków wynosi $7:9:12$ , ma boki długości $14 \sqrt{5}$ , $18 \sqrt{5}$ , $24 \sqrt{5}$ .

Kąty w trójkącie opisanym na okręgu

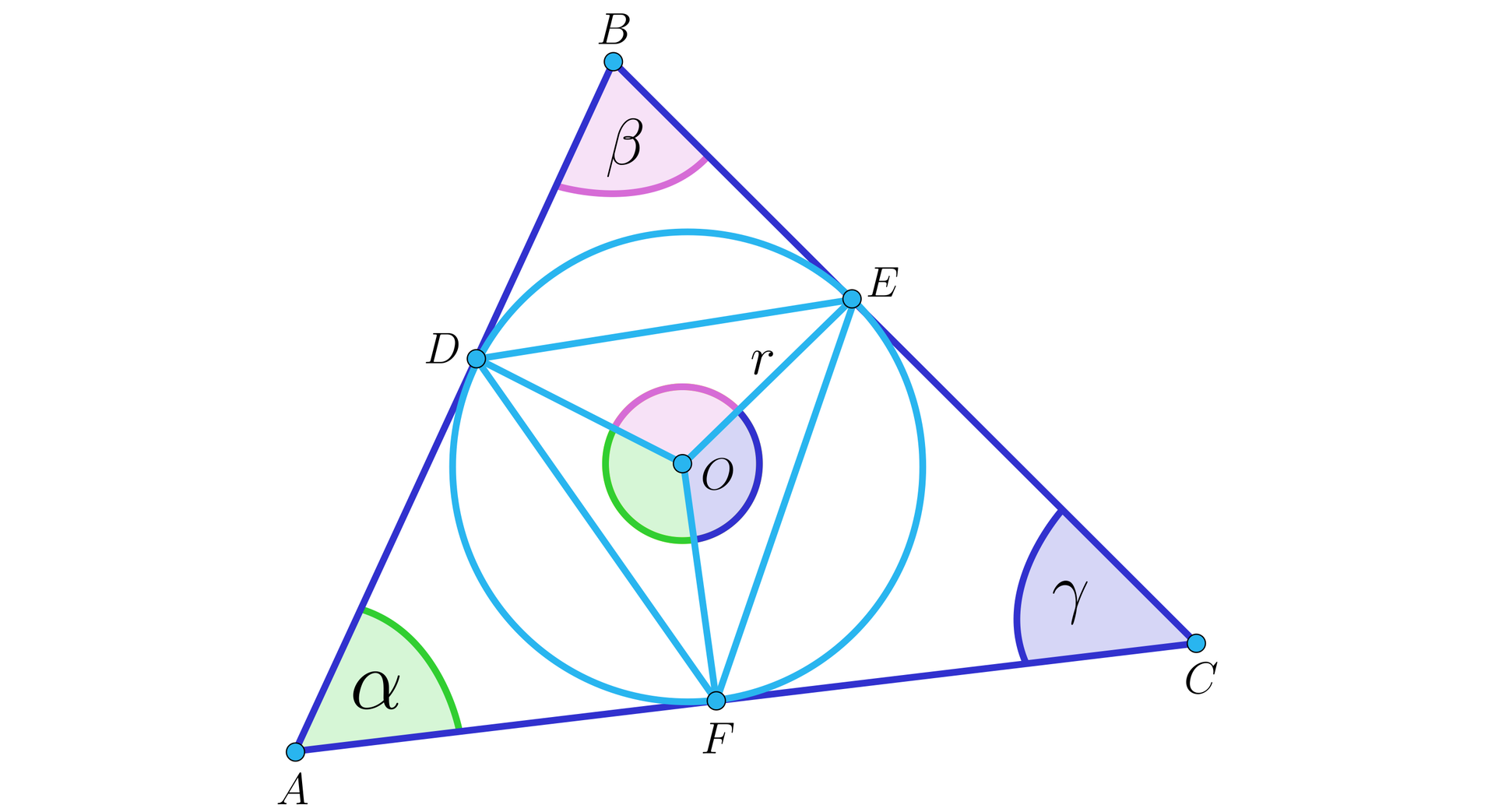
Na rysunku przedstawiony jest trójkąt $A B C$ opisany na okręgu o środku $O$ i promieniu $r$ . Punkty $D$ , $E$ , $F$ są punktami styczności. Tym samym kolorem oznaczone są kąty trójkąta i odpowiadające im kąty środkowe w okręgu.

RnePVrtg1gQK3

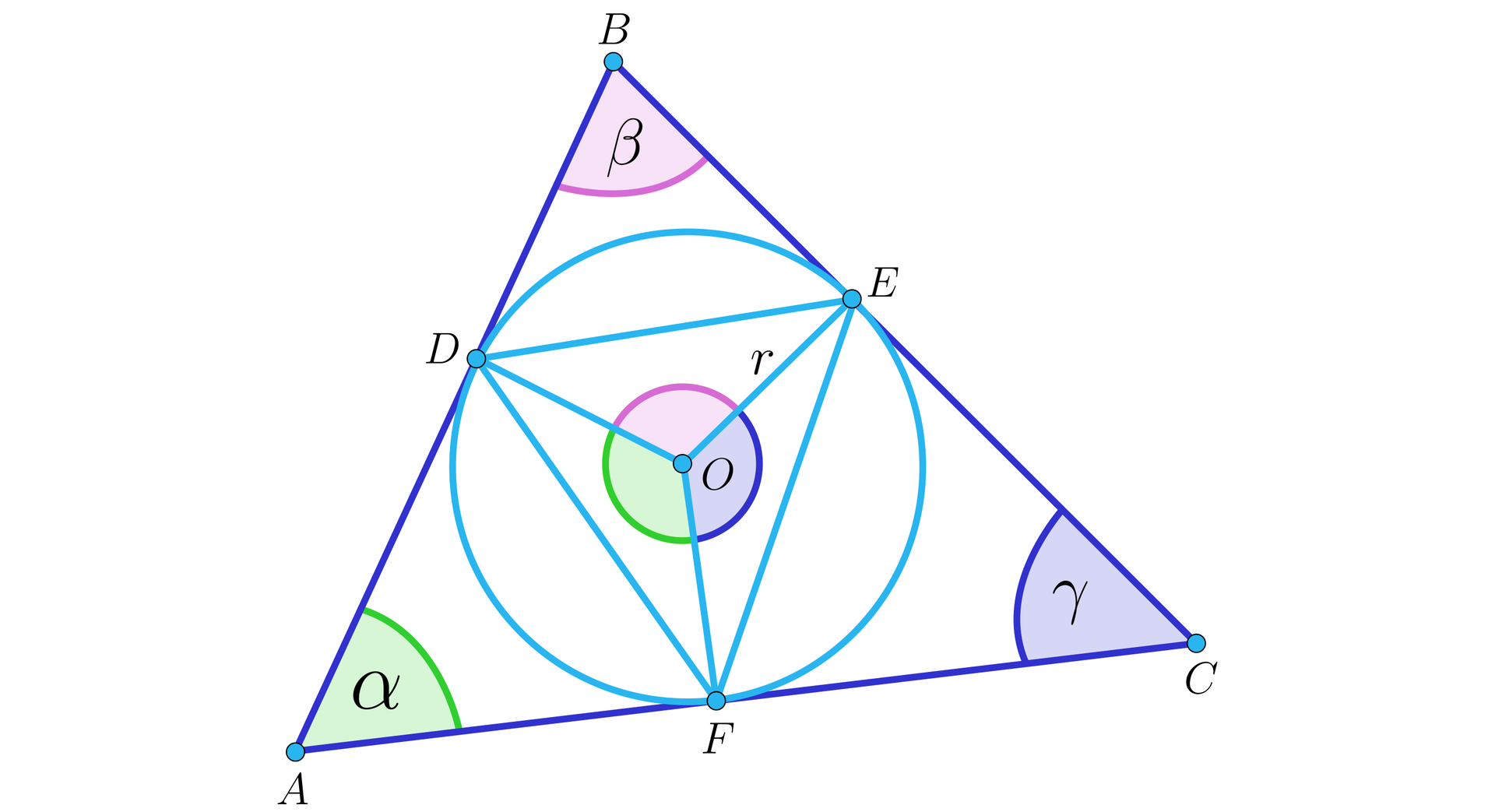
Ilustracja przedstawia trójkąt ABC, gdzie kąt ABC podpisano literą beta i oznaczono na różowo , kąt BCA podpisano literą gamma i oznaczono na niebiesko i kąt CAB podpisano literą alfa i oznaczono na zielono. W trójkąt ten wpisany jest okrąg o środku O który jest styczny z trójkątem ABC w punkcie D na boku AB , punkcie E na boku BC oraz punkcie F na boku AC. W okręgu zaznaczono również promienie o długości r które dochodzą do punków styku. Punkty styku są jednoczenie wierzchołkami trójkąta DEF wpisanego w okrąg. Kąt DOF oznaczony jest na zielono , DOE na różowo oraz FOE na niebiesko.

Wówczas kąty środkowe mają miary:

Kąt $D O F$ ma miarę $∢ D O F = 360 ° - 2 \cdot 90 ° - α = 180 ° - α$ , bo suma miar kątów w czworokącie wynosi $360 °$ oraz promienie okręgu poprowadzone do punktów styczności są prostopadłe do boków.
Analogicznie, $∢ D O E = 180 ° - β$ i $∢ E O F = 180 ° - γ$ .

Powyższa własność prowadzi do konstrukcji trójkąta opisanego na podstawie określenia punktów styczności:

Konstrukcja trójkąta opisanego na podstawie określenia punktów styczności

Własność: Konstrukcja trójkąta opisanego na podstawie określenia punktów styczności

Jeżeli na okręgu zaznaczone są trzy punkty $D$ , $E$ , $F$ takie, że kąty środkowe oparte na cięciwach $D E$ , $E F$ , $F D$ mają miary mniejsze od $180 °$ , to trójkąt, którego wierzchołkami są punkty przecięcia stycznych do okręgu w punktach $D$ , $E$ , $F$ , jest trójkątem opisanym na tym okręgu. Ponadto, każdy trójkąt opisany na okręgu można otrzymać w ten sposób.

Przykład 4

Pokażemy, że jeśli kąty środkowe oparte na cięciwach $D E$ , $E F$ , $F D$ mają miary równe $120 °$ , to trójkąt opisany na okręgu, styczny do tego okręgu w punktach $D$ , $E$ , $F$ jest trójkątem równobocznym.

Przy oznaczeniach z powyższego rysunku:

RnePVrtg1gQK3

$∢ D O F = 180 ° - α$ , więc $α = 180 ° - 120 ° = 60 °$ . Analogicznie pozostałe kąty.

Stąd trójkąt opisany na okręgu jest równoboczny.

Kąty w trójkącie, którego wierzchołkami są punkty styczności okręgu i trójkąta opisanego na okręgu

Rozważmy trójkąt $D E F$ , gdzie punkty $D$ , $E$ , $F$ są punktami styczności okręgu i trójkąta opisanego na okręgu.

R1IwtepPn6BgP

Wówczas kąty trójkąta $D E F$ mają miary:

$∢ D E F = \frac{1}{2} ∢ D O F = 90 ° - \frac{α}{2}$ , bo jest to kąt wpisany w okrąg oparty na tej samej cięciwiekąt wpisany w okrąg oparty na tej samej cięciwie co kąt środkowykąt środkowy $D O F$ .

Analogicznie, $∢ D F E = 90 ° - \frac{β}{2}$ i $∢ E D F = 90 ° - \frac{γ}{2}$ .

Wniosek:

Trójkąt $D E F$ , gdzie punkty $D$ , $E$ , $F$ są punktami styczności okręgu i trójkąta opisanego na okręgu jest trójkątem ostrokątnym. Ponadto, każdy trójkąt ostrokątny $D E F$ wpisany w okrąg wyznacza trójkąt opisany na tym okręgu taki, że punkty $D$ , $E$ , $F$ są punktami styczności okręgu i tego trójkąta.

Przykład 5

W okrąg wpisany jest trójkąt $D E F$ o kątach $50 °$ , $60 °$ , $70 °$ . Wyznaczymy kąty trójkąta opisanego na tym okręgu takiego, że punkty $D$ , $E$ , $F$ są punktami styczności okręgu i tego trójkąta.

Niech $α$ , $β$ , $γ$ oznaczają kąty tego trójkąta. Wtedy $50 ° = 90 ° - \frac{α}{2}$ , więc $α = 2 \cdot 90 ° - 2 \cdot 50 ° = 180 ° - 100 ° = 80 °$ oraz $β = 180 ° - 2 \cdot 60 ° = 60 °$ oraz $γ = 180 ° - 2 \cdot 70 ° = 40 °$ .

Zatem trójkąt ten ma kąty $40 °$ , $60 °$ , $80 °$ .

Słownik

podobieństwo figur

dwie figury nazywamy podobnymi, gdy istnieje podobieństwo o skali $k > 0$ , które przekształca jedną figurę w drugą.

cechy podobieństwa trójkątów

warunki konieczne i wystarczające na to, aby dwa trójkąty były podobne

kąt środkowy okręgu o środku

O

oparty na cięciwie

A B

kąt środkowy okręgu o środku

O

oparty na cięciwie

A B

kąt $A O B$ oparty na łuku $A B$ znajdujący się wewnątrz okręgu

kąt wpisany okręgu o środku

O

oparty na cięciwie

A B

kąt wpisany okręgu o środku

O

oparty na cięciwie

A B

kąt $A P B$ , gdzie $P$ jest punktem na okręgu leżącym po tej samej stronie cięciwy $A B$ co środek okręgu

Wprowadzenie

Animacja

Kąty w trójkącie opisanym na okręgu

Kąty w trójkącie, którego wierzchołkami są punkty styczności okręgu i trójkąta opisanego na okręgu

Słownik