Dany jest sześcian $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ o krawędzi długości $8$. Płaszczyzna przekroju przechodzi przez punkty $E$ i $F$, które są środkami krawędzi $AB$ i $BC$ odpowiednio oraz przez wierzchołek $B^{\text{'}}$. Obliczymy pole tego przekroju.

Rozwiązanie

Zróbmy rysunek pomocniczy.

Rr1S0iWjmX44Q

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Płaszczyzna przekroju przechodzi przez punkty E i F, które są środkami krawędzi AB i BC odpowiednio oraz przez wierzchołek B'.

Przekrój ten jest trójkątem. Co więcej, ponieważ $B^{\text{'}}E$ i $B^{\text{'}}F$ są przeciwprostokątnymi trójkątów $EB{B}^{\text{'}}$ i $BF{B}^{\text{'}}$ o przyprostokątnych $4$ i $8$, to $\left|B^{\text{'}}E\right|=\left|B^{\text{'}}F\right|$. A zatem trójkąt $E{B}^{\text{'}}F$ jest równoramienny.

Obliczmy długość ramion tego trójkąta z twierdzenia Pitagorasa (trójkąt $EB{B}^{\text{'}}$): $4^2+8^2={\left|B^{\text{'}}E\right|}^2$.

Czyli $\left|B^{\text{'}}E\right|=\sqrt{80}=4\sqrt{5}$.

Podstawa trójkąta $E{B}^{\text{'}}F$ jest przeciwprostokątną równoramiennego trójkąta prostokątnego $EBF$, którego przyprostokątne mają długość $4$. A zatem $\left|EF\right|=4\sqrt{2}$.

Narysujmy przekrój z zaznaczonymi odcinkami.

R1aTM5owNAh5h

Ilustracja przedstawia trójkąt równoramienny o ramieniu równym $4\sqrt{5}$ wysokość upuszczona na podstawę dzieli ją na dwa równe odcinki o długości $2\sqrt{2}$

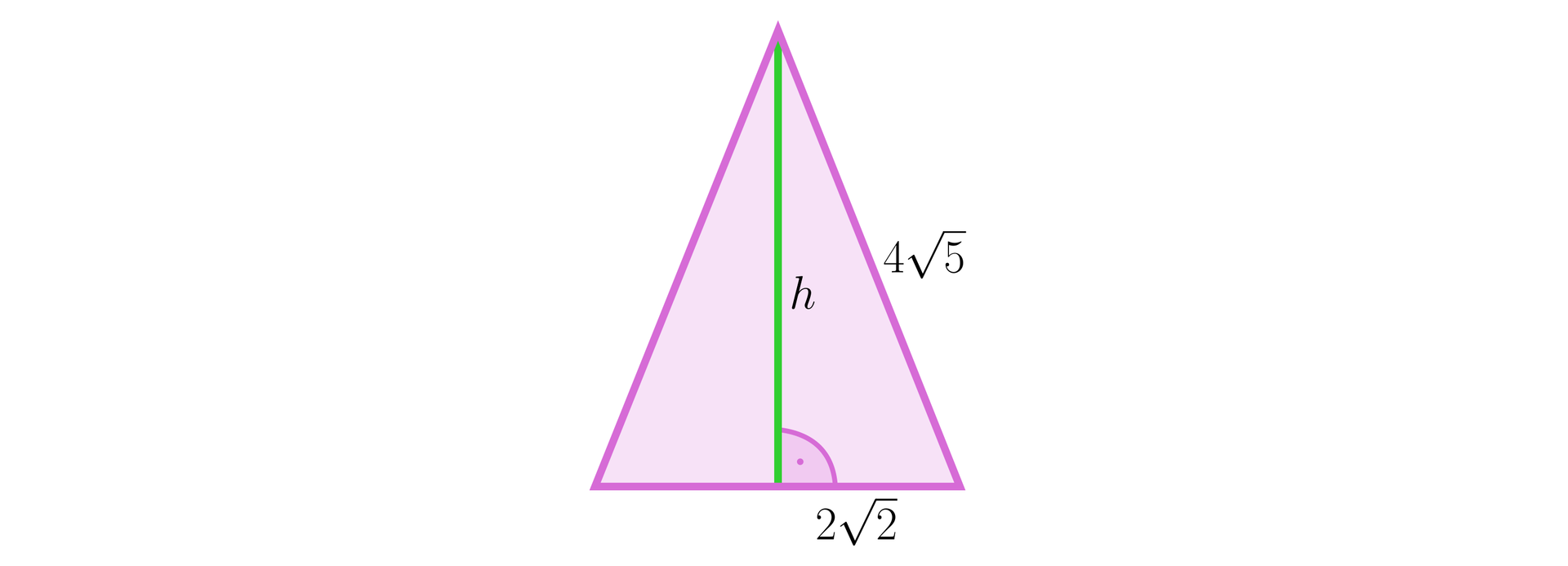
Obliczymy $h$ z twierdzenia Pitagorasa: $h^2+{\left(2\sqrt{2}\right)}^2={\left(4\sqrt{5}\right)}^2$. A stąd $h^2=80-8=72$.

Czyli $h=6\sqrt{2}$.

Teraz możemy już policzyć szukane pole przekroju: $P=\frac{4\sqrt{2}·6\sqrt{2}}{2}=24 {\mathrm{j}}^2$.

Pole przekroju sześcianu $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ przechodzącego przez wierzchołki $B^{\text{'}}C{D}^{\text{'}}$ wynosi $9\sqrt{3}{\mathrm{cm}}^2$. Obliczymy objętość tego sześcianu.

Rozwiązanie

Narysujmy ten przekrój:

RTZG8f5D2R0YV

Ilustracja przedstawia sześcian A B C D A prim B prim C prim D prim. Przez wierzchołki C B prim D prim przebiega płaszczyzna o kształcie trójkąta

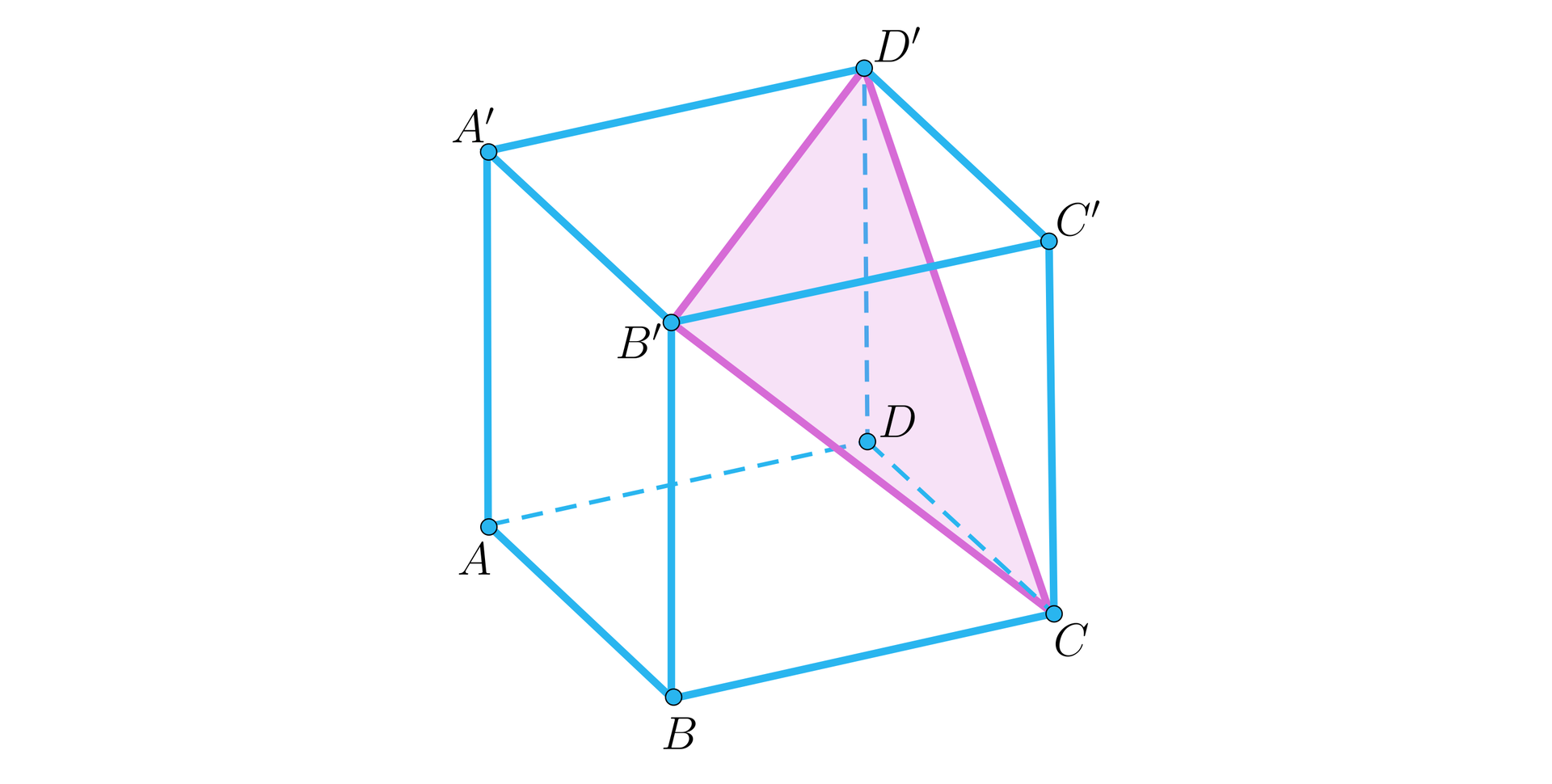
Przekrój ten jest trójkątem równobocznym. Obliczymy długość boku tego przekroju korzystając ze wzoru na pole trójkąta równobocznego: $\frac{p^2\sqrt{3}}{4}=9\sqrt{3}$. Stąd $p=6$. Ze wzoru na długość przekątnej ściany bocznej mamy $a\sqrt{2}=6$. Czyli $a=3\sqrt{2}$.

Objętość tego sześcianu wynosi więc $V={\left(3\sqrt{2}\right)}^3=54\sqrt{2}$.

Pole przekroju przechodzącego przez dwie krawędzie i dwie przekątne równoległych ścian sześcianuprzekątna sześcianuprzekątne równoległych ścian sześcianu wynosi $8\sqrt{2}$. Obliczymy długość krawędzi tego sześcianu.

Rozwiązanie

Narysujmy ten przekrój.

R13v5HNUSV2aZ

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Płaszczyzna przekroju w kształcie prostokąta przechodzi przez dwie krawędzie równoległych ścian bocznych A A prim oraz C C prim.

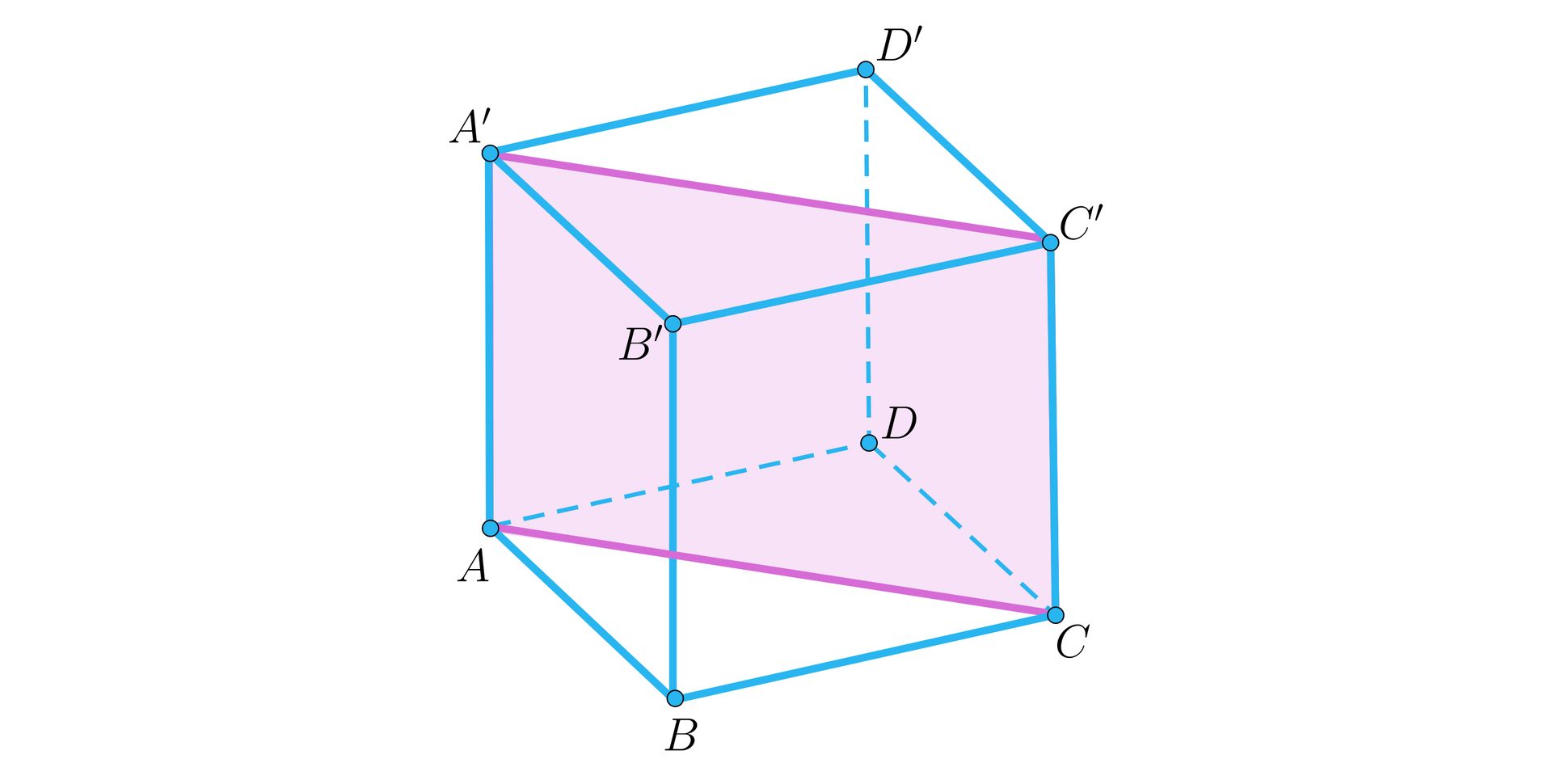
Jest to prostokąt, którego bokami są krawędzie i przekątne ścian. Pole tego prostokąta wyraża się więc wzorem $P=a·a\sqrt{2}=a^2\sqrt{2}$. Czyli $a^2\sqrt{2}=8\sqrt{2}$. Wtedy $a^2=8$, a stąd $a=2\sqrt{2}$.

Dany jest sześcian $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ o krawędzi długości $6$. Punkty $E$ i $F$ są środkami odcinków $CD$ i $A^{\text{'}}{B}^{\text{'}}$ odpowiednio. Określimy, jaką figurą jest przekrój $BE{D}^{\text{'}}F$ i ile wynosi jego pole.

Rozwiązanie

Zróbmy rysunek pomocniczy.

R1SJGIg1pdkfC

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Punkty E i F są środkami odcinków CD i A prim B prim odpowiednio. Płaszczyznę przeprowadzono przez punkty B E F D prim.

Zauważmy, że przekrój ten jest rombem. Narysujmy jego przekątne.

RnOBSw3PYFJHP

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Punkty E i F są środkami odcinków CD i A prim B prim odpowiednio. Płaszczyznę przeprowadzono przez punkty B E F D prim. Zaznaczono przekątną sześcianu B D prim. Równolegle do punktu F poprowadzono punkt G oraz do punktu E poprowadzono punkt H.

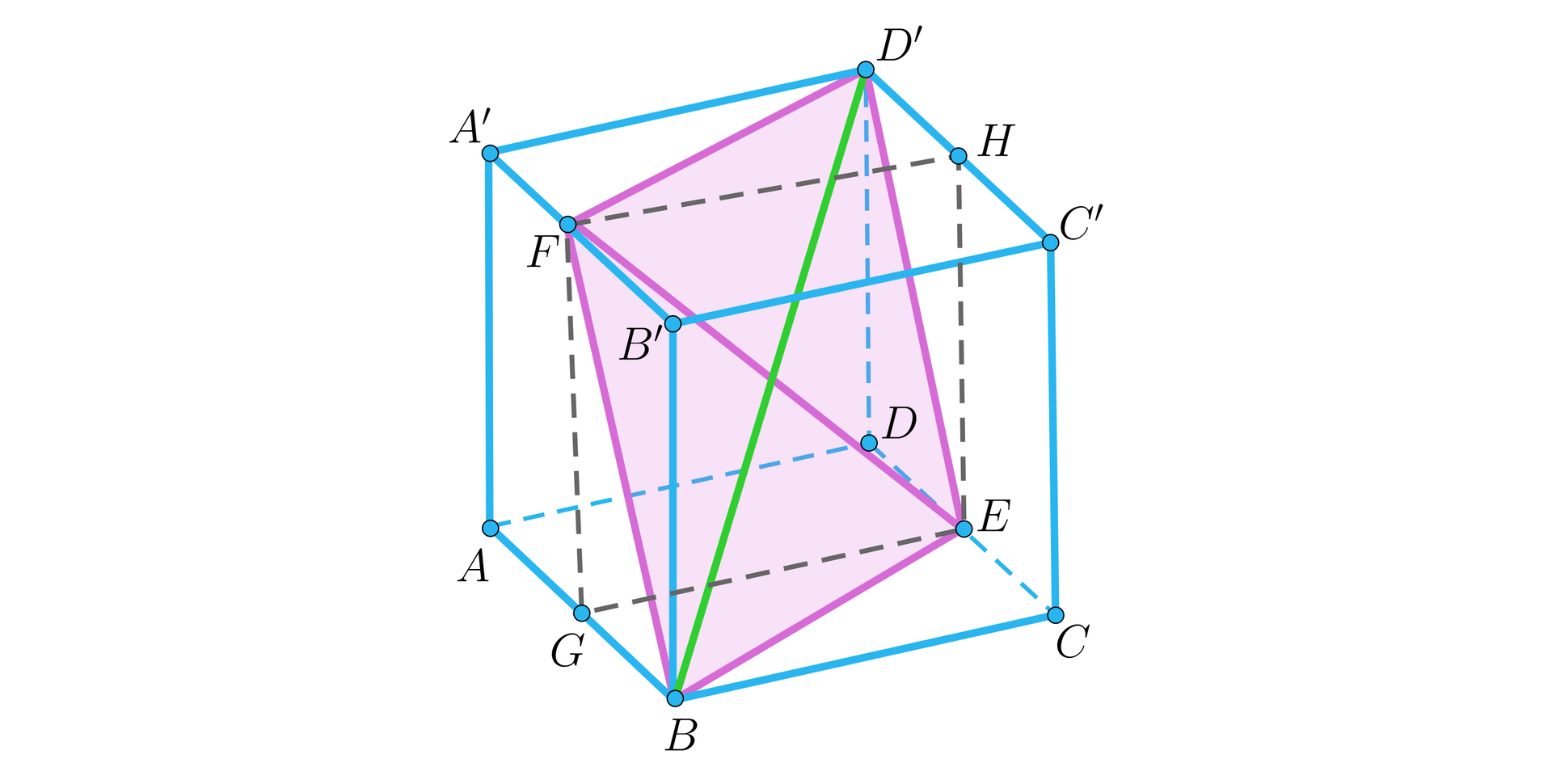
Zauważmy, że przekątna $B{D}^{\text{'}}$ jest przekątną sześcianu, a $FE$ jest przekątną kwadratu $EHFG$, który jest przystający do ścian sześcianu. Czyli $\left|B{D}^{\text{'}}\right|=6\sqrt{3}$ oraz $\left|EF\right|=6\sqrt{2}$. Obliczmy zatem pole tego przekroju: $P=\frac{6\sqrt{3}·6\sqrt{2}}{2}=18\sqrt{6} {\mathrm{j}}^2$.

Dany jest sześcian $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ o krawędzi $12$. Punkty $E$ i $F$ są środkami krawędzi $AB$ i $BC$. Obliczymy pole przekroju przechodzącego przez punkty $E$, $F$ i $D^{\text{'}}$.

Rozwiązanie

Zauważmy, że przekrój ten będzie pięciokątem.

R1eXPciVGLQ8Z

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Punkty E i F są środkami krawędzi podstawy AB i BC. Na krawędziach ścian bocznych A A prim oraz C C prim zaznaczono punkty kolejno G i P. Przez punkty E F G P i D prim przeprowadzono przekrój.

Podzielimy ten pięciokąt na trapez $EFPG$ oraz trójkąt $GP{D}^{\text{'}}$.

RTHSIVPUl2DQh

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Punkty E i F są środkami krawędzi podstawy AB i BC. Na krawędziach ścian bocznych A A prim oraz C C prim zaznaczono punkty kolejno G i P. Przez punkty E F G P i D prim przeprowadzono przekrój. Przez punkty G i P poprowadzono odcinek. Dzięki temu powstały dwie figury. Trójkąt GP D prim oraz trapez E F G P. Zaznaczono wysokości tych figur.

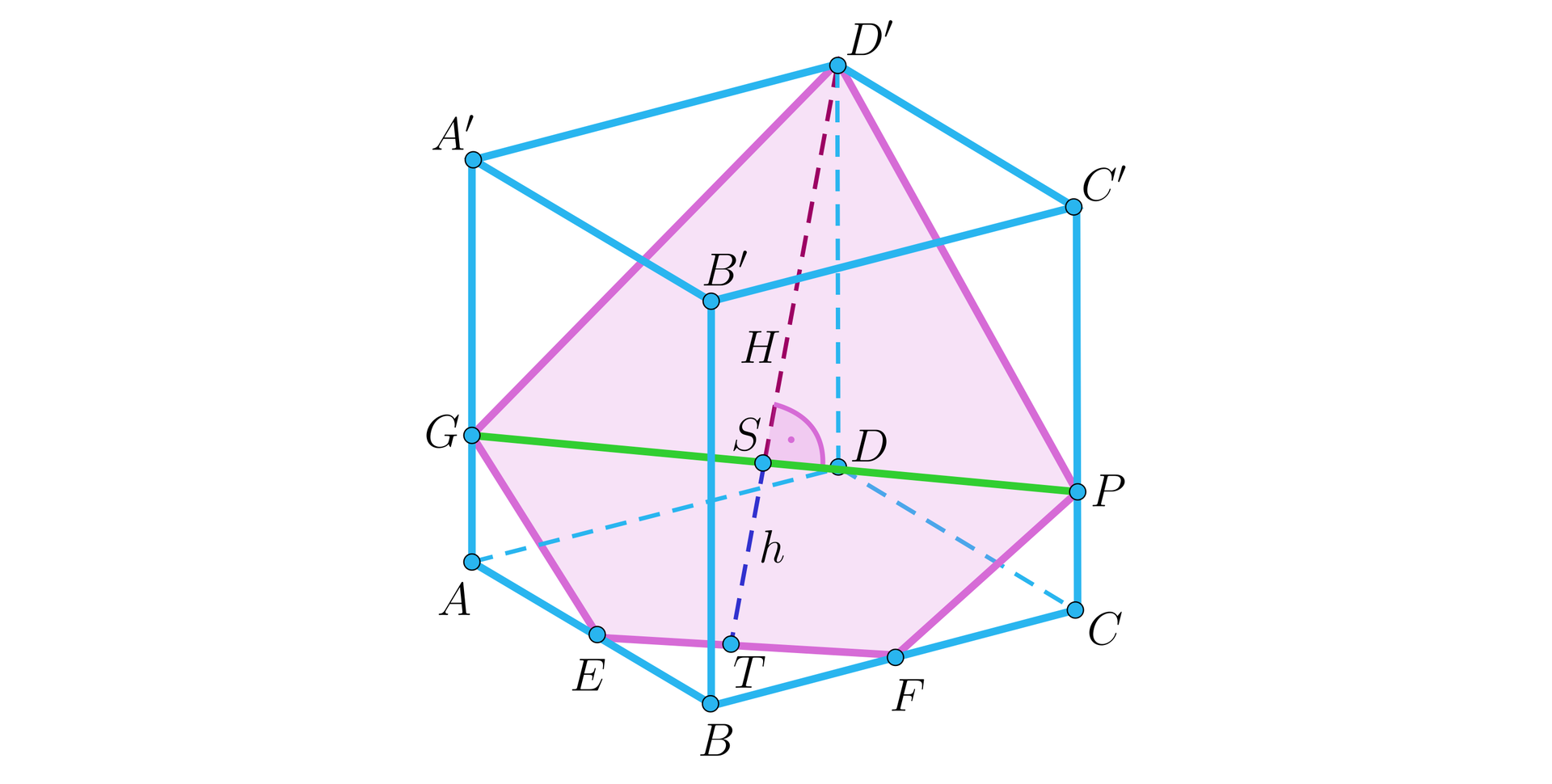
Zauważmy, że $\left|EF\right|=6\sqrt{2}$.

Obliczymy najpierw długość odcinka $T{D}^{\text{'}}$, którego długość jest równa sumie długości wysokości trójkąta $GP{D}^{\text{'}}$ i trapezu $EFPG$.

Skorzystamy z trójkąta prostokątnego $TD{D}^{\text{'}}$.

R1YIVoKMnJBfb

Ilustracja przedstawia sześcian A B C D A A prim B prim C prim D prim. Punkty E i F są środkami krawędzi podstawy odpowiednio punkt E krawędzi AB i punkt F krawędzi BC. Na krawędzi ściany bocznej A A prim oznaczono punkt G oraz na krawędzi ściany bocznej C C prim zaznaczono punkt P. Połączono punkty E oraz F i oznaczono ich środek T. Następnie zaznaczono trójkąt prostokątny T D D prim, gdzie przy wierzchołku D znajduje się kąt prosty. Na przeciwprostokątnej T D prim tego trójkąta zaznaczono punkt S, następnie odcinek T  S podpisano jako h oraz odcinek H D prim oznaczono jako H, gdzie h jest mniejsze od H.

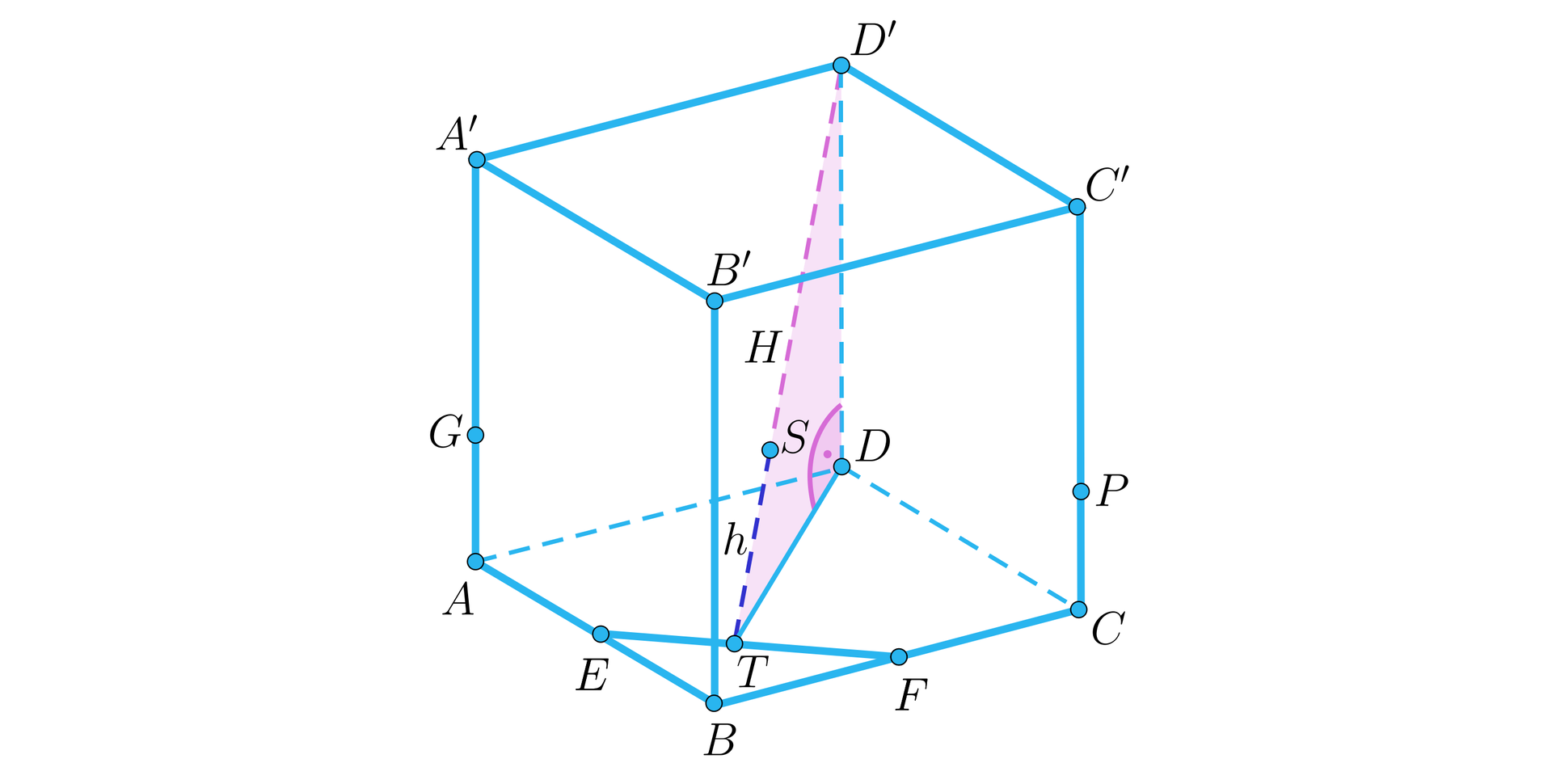
Najpierw zauważmy, że $\left|TD\right|=\frac{3}{4}\left|BD\right|=\frac{3}{4}·12\sqrt{2}=9\sqrt{2}$. (wynika to z podobieństwa trójkątów $BEF$ i $BAC$ – ponieważ boki trójkąta $BEF$ są o połowę krótsze od boków trójkąta $BAC$, to odcinek $BT$, który jest wysokością trójkąta $BEF$ stanowi połowę połowy przekątnej kwadratu, czyli $\left|BT\right|=\frac{1}{4}\left|BD\right|$.

Obliczmy teraz długość odcinka $T{D}^{\text{'}}$ z twierdzenia Pitagorasa dla trójkąta $TD{D}^{\text{'}}$:

${\left(9\sqrt{2}\right)}^2+{12}^2={\left|T{D}^{\text{'}}\right|}^2$

Czyli $\left|T{D}^{\text{'}}\right|=3\sqrt{34}$.

W trójkącie $TD{D}^{\text{'}}$ poprowadźmy prostą równoległą do $TD$ przez punkt $S$

R1TigHj9gbrmx

Ilustracja przedstawia trójkąt T D D prim. Podstawa T D ma miarę $9\sqrt{2}$. Odcinek S U o mierze $6\sqrt{2}$ dzieli ten trójkąt na dwa mniejsze. Odcinek S T ma miarę h równą $3\sqrt{34}-H$

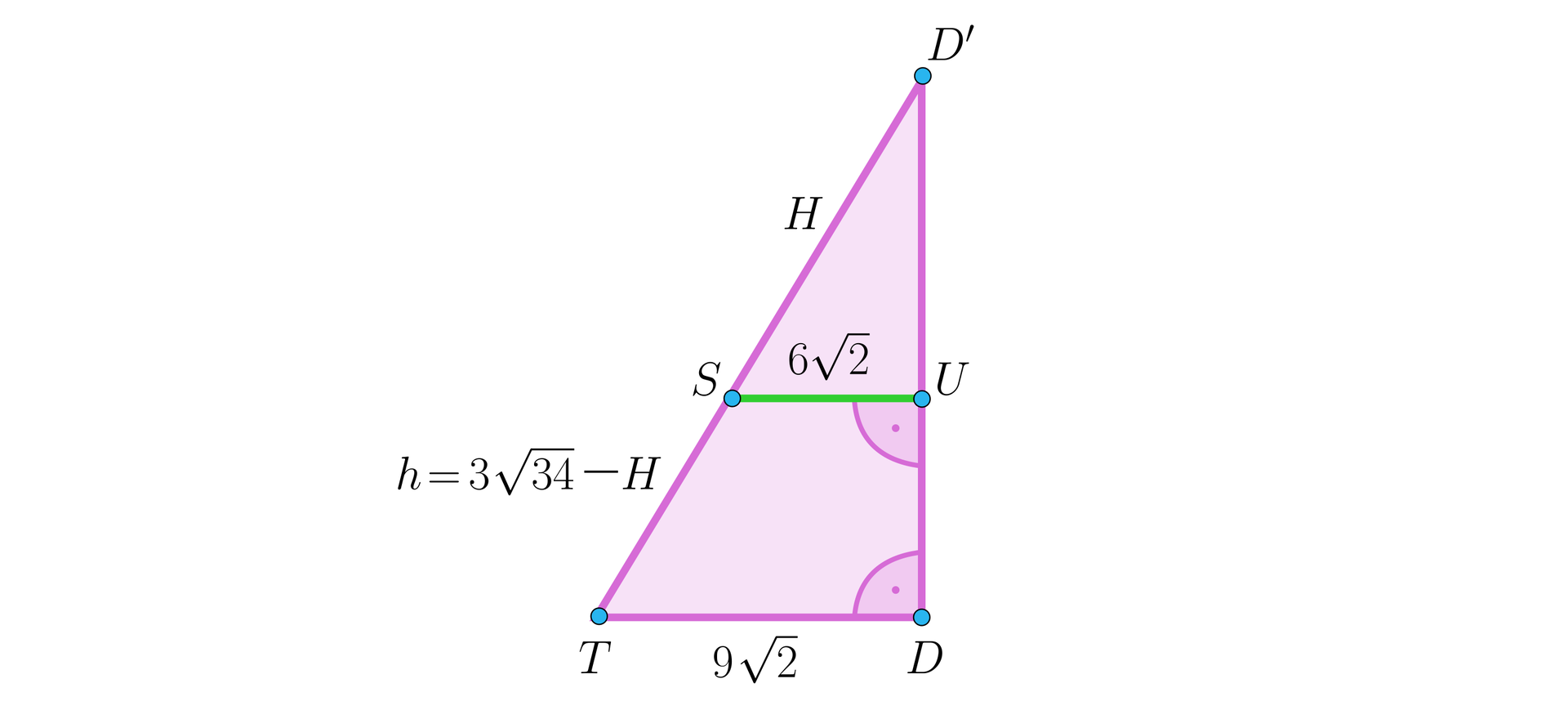
Z podobieństwa trójkątów $TD{D}^{\text{'}}$ i $SU{D}^{\text{'}}$ (cecha $kkk$) mamy więc $\frac{H}{3\sqrt{34}}=\frac{6\sqrt{2}}{9\sqrt{2}}$.

Czyli $\frac{H}{3\sqrt{34}}=\frac{2}{3}$. A stąd $H=2\sqrt{34}$ i $h=\sqrt{34}$.

Obliczymy pole trapezu $EFPG$:

$P_1=\frac{\left(6\sqrt{2}+12\sqrt{2}\right)·\sqrt{34}}{2}=9\sqrt{68}=18\sqrt{17}$

Oraz pole trójkąta $GP{D}^{\text{'}}$:

$P_2=\frac{12\sqrt{2}·2\sqrt{34}}{2}=12\sqrt{68}=24\sqrt{17}$

Ostatecznie pole przekroju wynosi $P=18\sqrt{17}+24\sqrt{17}=42\sqrt{17} {\mathrm{j}}^2$.

Obliczymy pole całkowite sześcianu $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ którego przekrój przechodzący przez środki krawędzi $A{A}^{\text{'}}$, $AB$, $BC$ ma pole równe $96\sqrt{3}$.

Rozwiązanie

Zauważmy, że przekrój ten będzie sześciokątem foremnym.

R1YfWqTBxC7OE

Ilustracja przedstawia sześcian A B C D A prim B prim C prim D prim. Na środkach krawędzi podstawy powstały punkty E F H P. Na środkach dwóch ścian bocznych powstały punkty G i Q. Przez punkty E F Q P H G przeprowadzono przekrój w kształcie sześciokąta

Korzystając ze wzoru na pole sześciokąta foremnego mamy $6·\frac{{\left|FQ\right|}^2\sqrt{3}}{4}=96\sqrt{3}$. Czyli ${\left|FQ\right|}^2=64$, a stąd $\left|FQ\right|=8$.

Odcinek $FQ$ jest przeciwprostokątną trójkąta prostokątnego równoramiennego o przyprostokątnej długości $\frac{a}{2}$, gdzie $a$ jest długością krawędzi sześcianu. Czyli $\frac{a}{2}\sqrt{2}=8$, a stąd $a\sqrt{2}=16$ i ostatecznie $a=8\sqrt{2}$. Czyli pole powierzchni tego sześcianupole powierzchni sześcianupole powierzchni tego sześcianu wynosi $P_c=6a^2=768 {\mathrm{j}}^2$.

figura, która jest częścią wspólną sześcianu i pewnej płaszczyzny, która go przecina

odcinek, który łączy wierzchołki dolnej i górnej podstawy sześcianu nie leżące na jednej ścianie tego sześcianu

suma pól wszystkich ścian tego sześcianu