Przeczytaj

Ważne!

Przypomnijmy najważniejsze informacje o trójkątach. Wykorzystamy je przy konstrukcji kąta ostrego, gdy mamy daną wartość jednej z funkcji trygonometrycznych tego kąta.

Przyjmijmy oznaczenia jak na rysunku:

R1BpGwcaWJskG

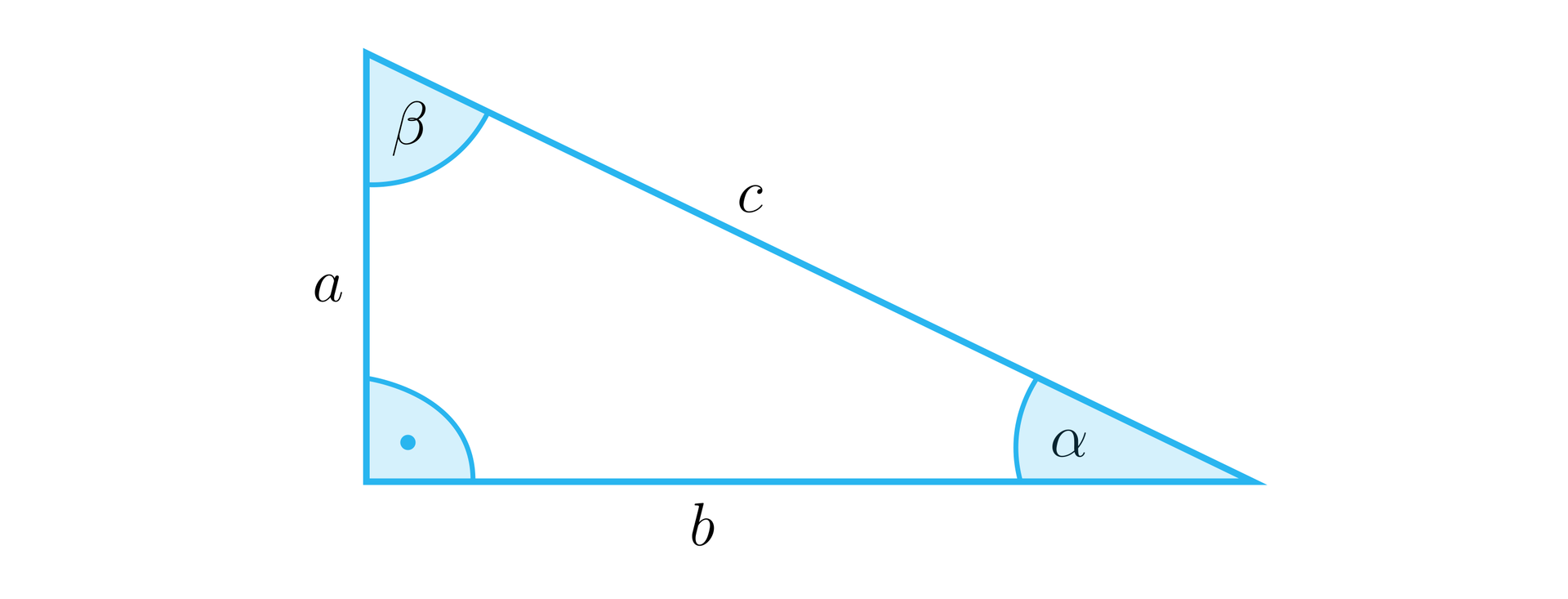
Ilustracja przedstawia trójkąt prostokątny o pionowej przyprostokątnej a, poziomej przyprostokątnej b i przeciwprostokątnej c. Kąty wewnętrzne trójkąta: między bokami a i b zaznaczono kąt prosty, między bokami b i c jest kąt alfa, między bokami a i c jest kąt beta.

Twierdzenie Pitagorasa:
$a^{2} + b^{2} = c^{2}$
Funkcje trygonometryczne kąta ostrego $α$ Funkcje trygonometryczne kąta ostrego $α$ :
$\sin α = \frac{a}{c}$
$\cos α = \frac{b}{c}$
$tg α = \frac{a}{b}$

Przykład 1

Załóżmy, że chcemy narysować kąt $α$ , dla którego $tg α = \frac{1}{3}$ .

Nie jest to żaden problem w zeszycie w kratkę. Wystarczy narysować prostopadłe odcinki, których punktem wspólnym są ich końce tak, by jeden był trzy razy dłuższy od drugiego.

Na przykład:

ReyNxPiwrAPIA

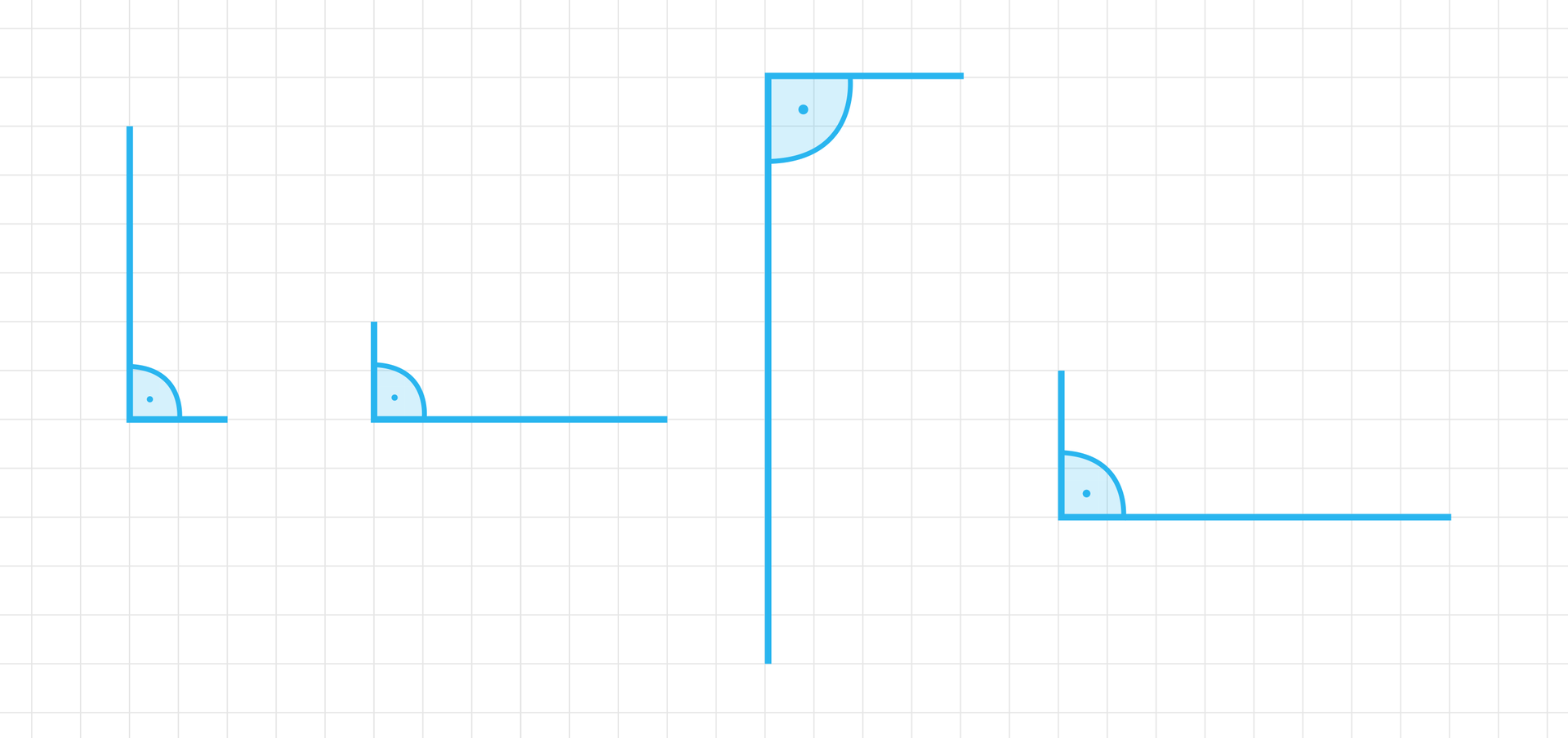
Ilustracja przedstawia prostopadłe odcinki między którymi oznaczono kąty proste. Kąty i odcinki narysowano na tle w kratkę. Od lewej mamy: pionowy odcinek o długości sześciu kratek. Od dolnego końca odcinka odchodzi poziomy na dwie kratki i między nimi oznaczono kąt prosty. Następnie mamy pionowy odcinek o długości dwóch kratek. Od dolnego końca odcinka odchodzi poziomy na sześć kratek. Między odcinkami oznaczono kąt prosty. Następnie mamy pionowy odcinek o długości dwunastu kratek. Od górnego końca odcinka odchodzi poziomy na 4 kratki. Między odcinkami oznaczono kąt prosty. Następnie mamy pionowy odcinek o długości czterech kratek. Od dolnego końca odcinka odchodzi poziomy na 12 kratek. Między odcinkami oznaczono kąt prosty.

A następnie zbudować trójkąt prostokątny i właściwie wskazać kąt $α$ .

Rq5dOEeRyMrCC

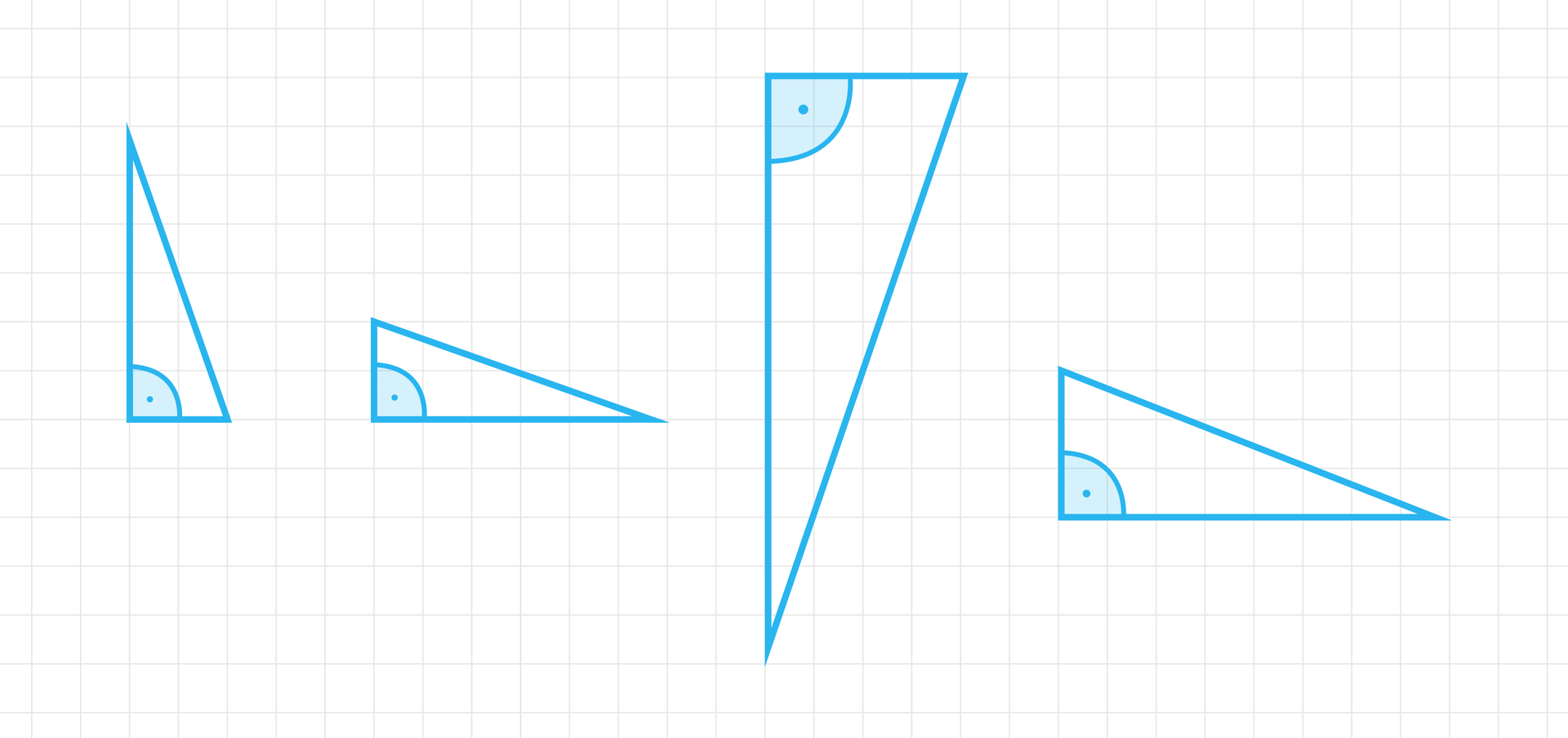
Ilustracja przedstawia cztery różne trójkąty prostokątne w różnym położeniu. W każdym trójkącie oznaczono kąt prosty.

Oczywiście $tg α = \frac{1}{3}$ .

Przykład 2

Trudność pojawi się, gdy będziemy mieli za zadanie skonstruowaćskonstruowaćskonstruować kąt $α$ , którego tangens to $\sqrt{5}$ .

Musimy wtedy skonstruować prostopadłe odcinki, których stosunek jest jak $1 : \sqrt{5}$ . Najłatwiej więc wybrać odcinki długości $1$ oraz $\sqrt{5}$ .

Jak skonstruować odcinek o długości $\sqrt{5}$ ? Wystarczy skorzystać z Twierdzenia Pitagorasa i zacząć od narysowania trójkąta prostokątnego o bokach długości $1$ i $2$ .

Nadal możemy korzystać z kratek w zeszycie. Wówczas długość przeciwprostokątnej to $\sqrt{1^{2} + 2^{2}}$ , czyli właśnie $\sqrt{5}$ .

RSqlAgt95Xn0Q

Ilustracja przedstawia trójkąt prostokątny o pionowej przyprostokątnej o długości 2 centymetry, poziomej przyprostokątnej o długości 1 centymetr i przeciwprostokątnej o długości pierwiastek kwadratowy z pięciu centymetrów. W trójkącie oznaczono kąt prosty.

Teraz wróćmy do szukanego kąta. Narysujmy odcinek długości $1$ i prostopadłą do niego półprostą o początku w jednym z końców odcinka.

Na tej półprostej, za pomocą cyrkla, odmierzamy długość $\sqrt{5}$ , a następnie rysujemy trójkąt prostokątny i wskazujemy kąt $α$ .

R14tf7vbB4L7n

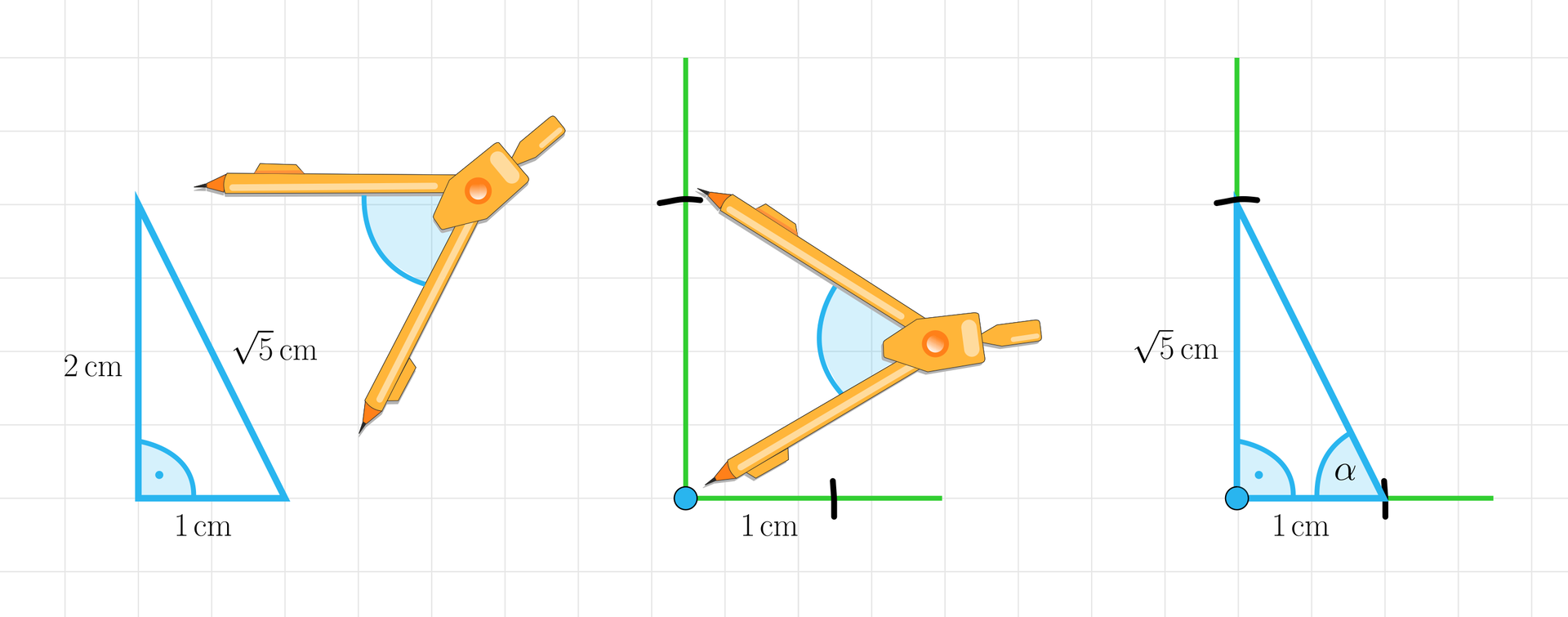
Ilustracja składa się z trzech części. Pierwsza część przedstawia trójkąt prostokątny o bokach o następujących długościach: pozioma przyprostokątna ma długość 1, pionowa przyprostokątna ma długość 2, a przeciwprostokątna ma długość pierwiastek kwadratowy z pięciu centymetrów. Obok trójkąta narysowano rozłożony cyrkiel. Druga część przedstawia pionowy odcinek o długości sześciu kratek. Od dolnego końca odcinka odchodzi poziomy odcinek o długości czterech kratek. Na obu odcinkach odłożono cyrklem długości przyprostokątnych trójkąta, licząc od wspólnego środka odcinków. Na pionowym odcinku odłożono długość przeciwprostokątnej, czyli pierwiastek kwadratowy z pięciu centymetrów, a na poziomym 1 centymetr. Trzecia część rysunku przedstawia przekształcony trójkąt rozrysowany na odcinkach. Pionowa przyprostokątna ma długość pierwiastek kwadratowy z pięciu centymetrów, pozioma przyprostokątna ma długość 1, a między bokiem o długości 1 i przeciwprostokątną zaznaczono kąt alfa.

Oczywiście $tg α = \sqrt{5}$ .

Przykład 3

Jak narysować kątkątkąt $α$ , dla którego $tg α = \frac{\sqrt{3}}{3}$ ?

Tutaj mamy dwie możliwości. Pierwsza, trudniejsza, wymaga abyśmy najpierw narysowali odcinek o długości $\sqrt{3}$ .

Nie jest to tak łatwe jak narysowanie odcinka o długości $\sqrt{5}$ !

Możemy podejść ambicjonalnie i próbować, jednak tym razem uciekniemy się do łatwiejszej metody.

Przede wszystkim powinniśmy mieć już w pamięci tablicę funkcji trygonometrycznych kątów szczególnych.

$α$	$30 °$	$45 °$	$60 °$
$\sin α$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$
$\cos α$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$
$tg α$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$

Wiemy stąd, że szukany kąt ma miarę $30 °$ . Jest to więc połowa kąta $60 °$ , a przecież $60 °$ to miara kąta wewnętrznego trójkąta równobocznego.

Narysujmy odcinek, a dla ułatwienia załóżmy, że ma parzystą liczbę kratek.

Odmierzmy długość odcinka cyrklem, z obu końców odcinka zaznaczając łuki. Punkt przecięcia łuków, to wierzchołek trójkąta równobocznego.

RiuaAp3s9v2K1

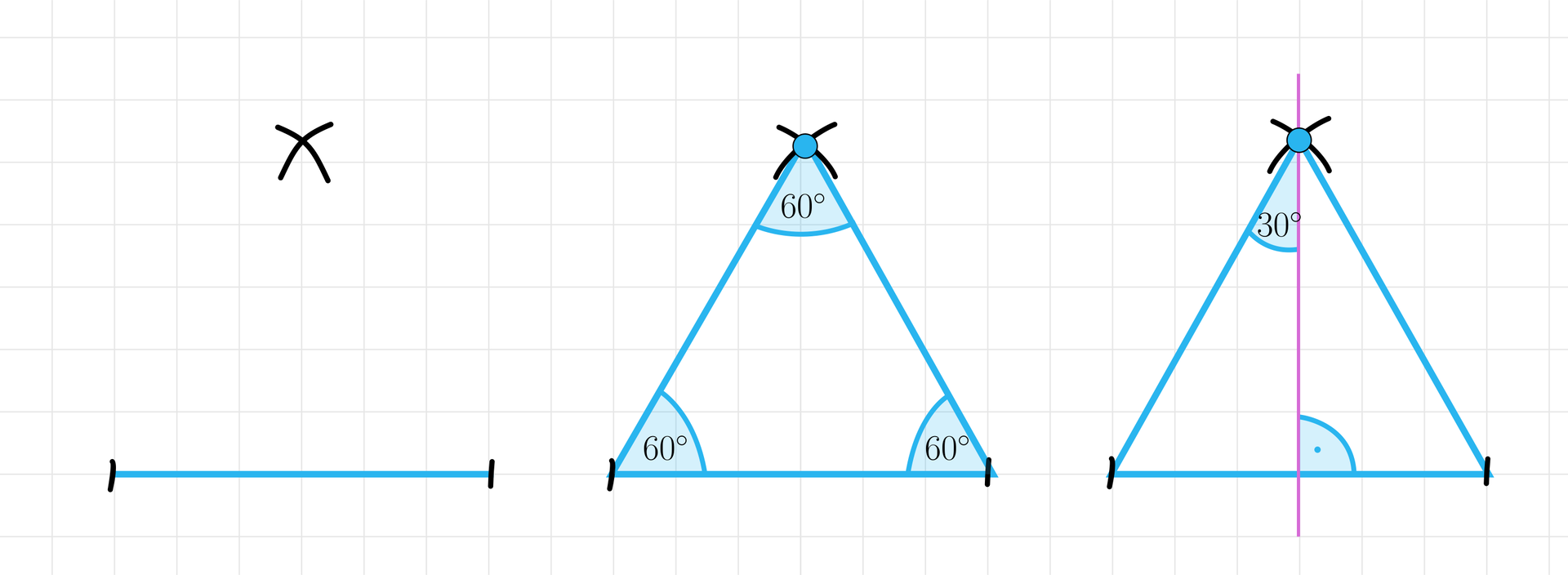
Ilustracja składa się z trzech części. Pierwsza część to poziomy odcinek o długości sześciu kratek. Nad odcinkiem zaznaczono punkt leżący nad środkiem odcinka w odległości od każdego z końców odcinka równej długości poziomego odcinka, który wyznaczono przy pomocy cyrkla. Druga część rysunku przedstawia trójkąt narysowany w oparciu o ten poziomy odcinek, Dorysowane dwa boki o tej samej długości, co poziomy odcinek, które poprowadzono do wyznaczonego odcinka. Uzyskano w ten sposób trójkąt równoboczny, w którym zaznaczono kąty wewnętrzne, z których każdy równy jest 60 stopni. Trzecia część ilustracji przedstawia ten sam trójkąt równoboczny podzielony wzdłuż pionową prostą przebiegającą przez górny wierzchołek i środek podstawy trójkąta. Prosta przecina podstawę pod kątem prostym, co oznaczono. Przy górnym wierzchołku między lewym bokiem a prostą oznaczono kąt 30 stopni.

Każdy z kątów tego trójkąta ma miarę $60 °$ .

Pamiętajmy, że w trójkącie równobocznym wysokość trójkąta jest też dwusieczną jego kąta.

Pozostaje już tylko dorysować wysokość i zaznaczyć kąt $α$ .

RyVNGVjNFZ5u1

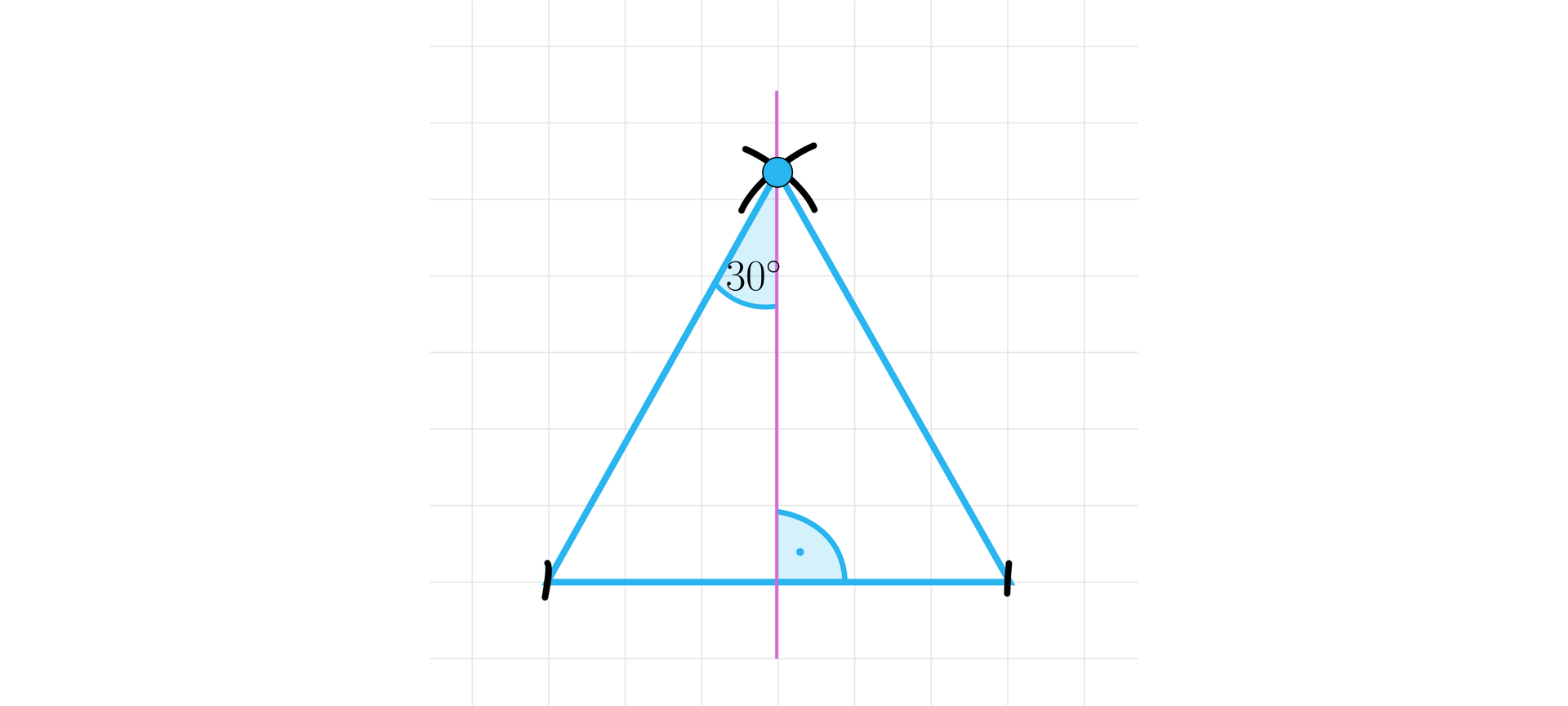
Ilustracja przedstawia trójkąt równoboczny podzielony wzdłuż pionową prostą przebiegającą przez górny wierzchołek i środek podstawy trójkąta. Prosta przecina podstawę pod kątem prostym, co oznaczono. Przy górnym wierzchołku między lewym bokiem a prostą oznaczono kąt 30 stopni.

Przykład 4

Umiemy już narysować kąt znając wartość jego tangensa. Co, jeśli zostaniemy poproszeni o narysowanie takiego kąta ostrego $α$ , by zachodziła równość $\sin α = 0, 8$ ?

Pokażemy dwa sposoby podejścia do tego problemu.

Sposób I:

Dla ułatwienia zauważmy, że $\sin α = 0, 8 = \frac{4}{5}$ .

Możemy od razu założyć, że w naszym trójkącie jedna z przyprostokątnych ma długość $4$ a przeciwprostokątna ma długość $5$ . Musimy narysować odcinek $A B$ o długości $4$ a następnie za pomocą cyrkla odmierzyć odcinek o długości $5$ , którego jednym z końców jest punkt $B$ a drugi koniec leży na półprostej prostopadłej do odcinka $A B$ zaczynającej się w punkcie $A$ .

R1YJgQiQjbxHq

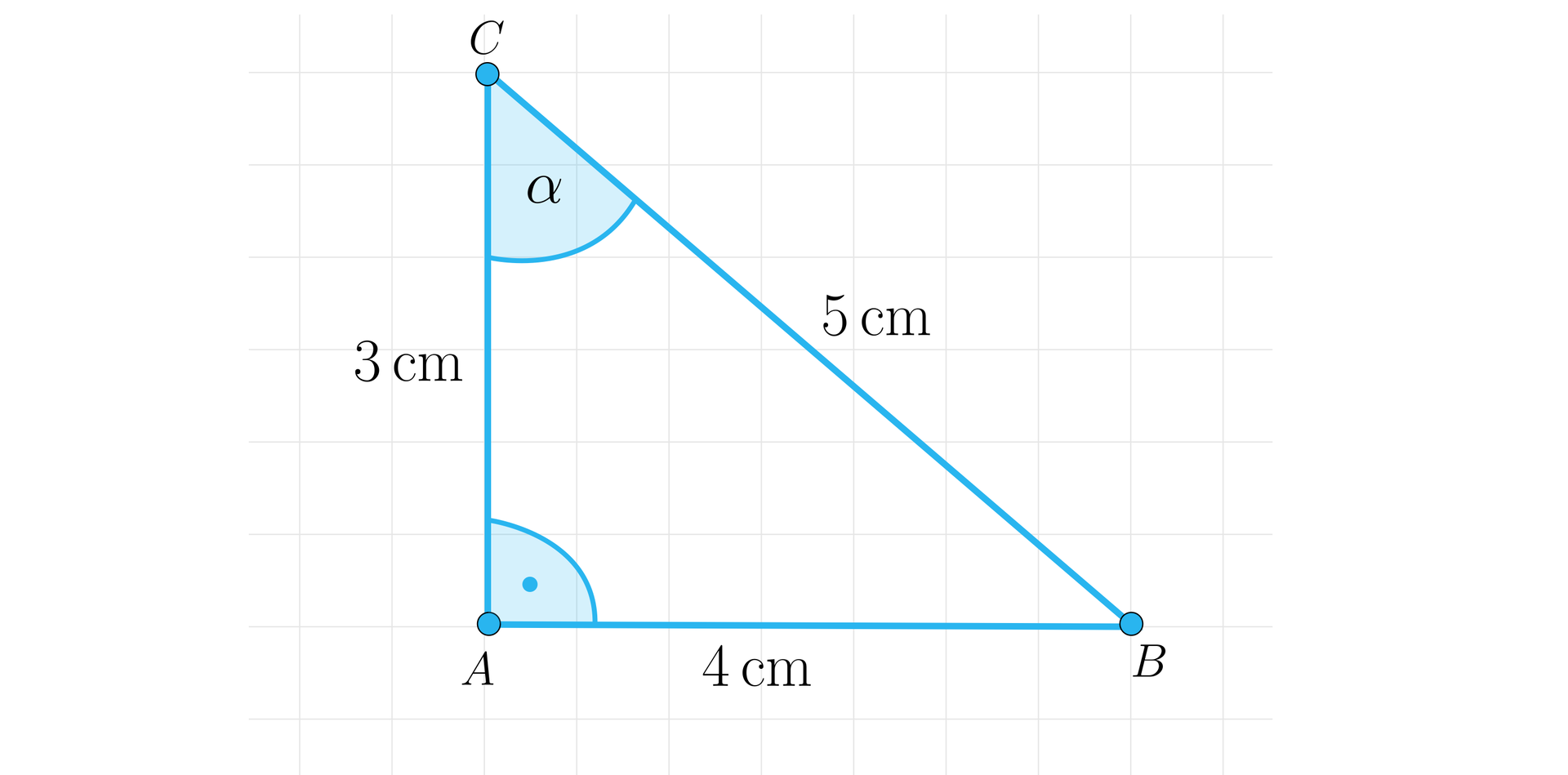
Ilustracja przedstawia trójkąt prostokątny A B C o pionowej przyprostokątnej C A o długości 3 centymetry, poziomej przyprostokątnej A B o długości 4 centymetry oraz o przeciwprostokątnej B C o długości 5 centymetrów.

Oczywiście $\sin α = \frac{4}{5} = 0, 8$ .

Sposób II:

Korzystając z tożsamości trygonometrycznych obliczymy $tg α$ .

Przypomnijmy, że $tg α = \frac{\sin α}{\cos α}$ .

Z kolei z jedynki trygonometrycznej wiemy, że

$\cos^{2} α = 1 - \sin^{2} α$

$\cos^{2} α = 1 - 0, 8^{2}$

$\cos^{2} α = 0, 36$

$\cos α = 0, 6$

Zatem $tg α = \frac{0, 6}{0, 8} = \frac{3}{4}$ .

W powyższym przykładzie sprowadziliśmy problem narysowania kąta o zadanym sinusie do problemu narysowania kąta o zadanym tangensie, a z tym umiemy już sobie poradzić.

Wystarczy narysować prostopadłe odcinki, których punktem wspólnym są ich końce tak, by stosunek ich długości był $3 : 4$ .

RjAhih1OmFEPK

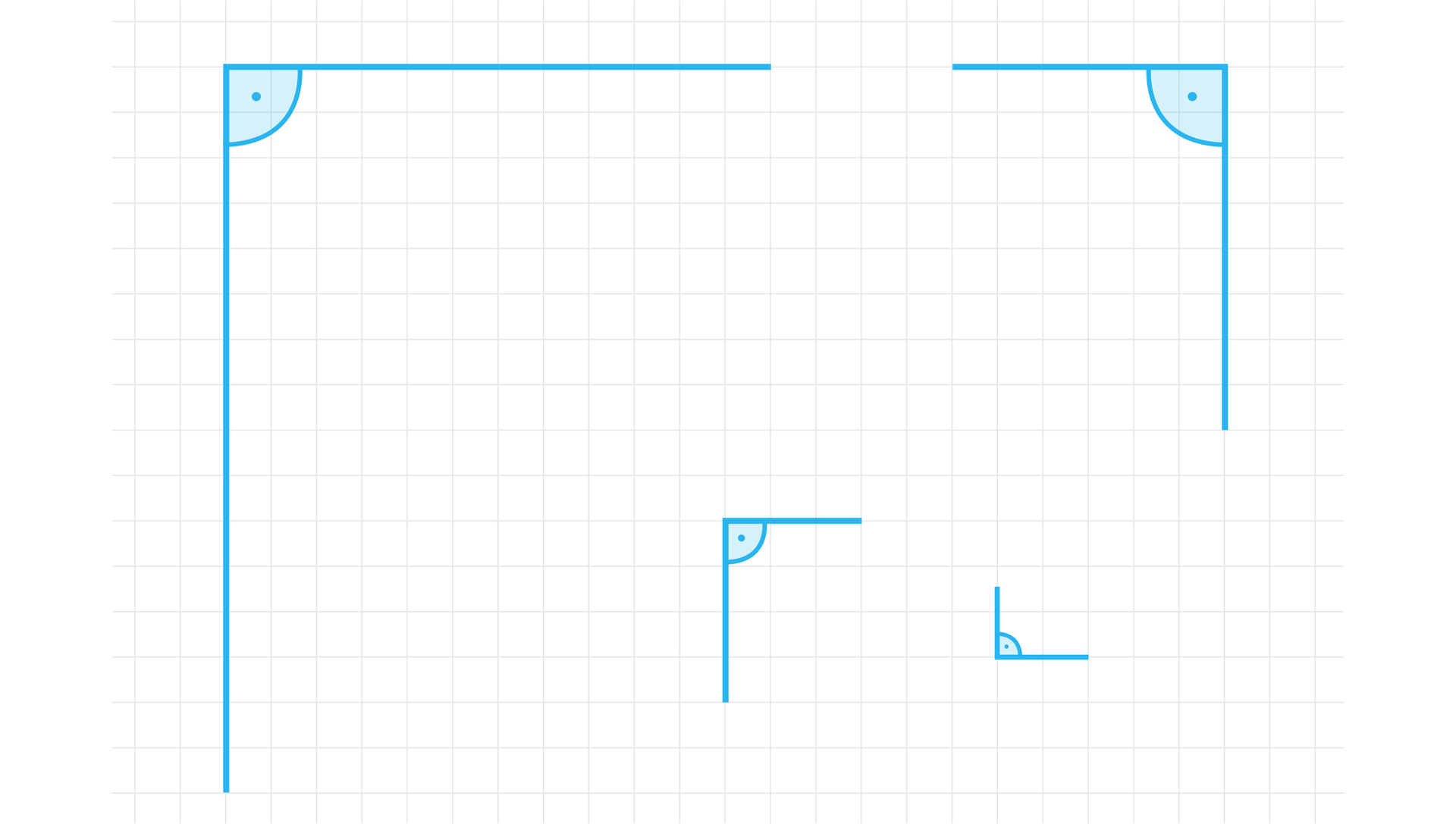
Ilustracja przedstawia kilka prostopadłych do siebie parami odcinków między którymi oznaczono kąt prosty. Mamy kolejno pionowy odcinek o długości 16 kratek. Od jego górnego końca poprowadzono poziomy odcinek o długości 12 kratek i zaznaczono między nimi kąt prosty. Następna para odcinków to pionowy odcinek o długości czterech kratek, od którego górnego końca poprowadzono poziomy odcinek o długości 3 kratki. Między odcinkami zaznaczono kąt prosty. Kolejna para odcinków to pionowy odcinek o długości półtorej kratki, od którego dolnego końca odchodzi poziomy odcinek o długości dwóch kratek. Między nimi oznaczono kąt prosty. Czwarta para odcinków to poziomy odcinek o długości sześciu kratek. Z jego prawego końca poprowadzono pionowy odcinek o długości ośmiu kratek. Między nimi zaznaczono kąt prosty.

A następnie narysować odpowiednie trójkąty i zaznaczyć właściwy kąt.

R1h6pTzH3jpHe

Ilustracja przedstawia cztery różne trójkąty prostokątne w różnym położeniu. W każdym trójkącie oznaczono kąt prosty i kąt alfa.

Problem narysowania kątakątkąta znając jego cosinus jest symetryczny do sytuacji gdy znamy wartość sinusa.

Przykład 5

Co powinniścmy odpowiedzieć, jeśli zostaniemy poproszeni o narysowanie kąta, którego sinus wynosi $2$ ?

R6l7EwsVJE1X3

W całej lekcji nie użyliśmy słowa „skonstruowaćskonstruowaćskonstruować”, choć omawianym zagadnieniem jest Konstrukcja kąta ostrego o danej funkcji trygonometrycznej. Dlaczego? Chcemy trzymać się określonej już w starożytności przez Platona zasady, że „konstruując” możemy korzystać jedynie z cyrkla i linijki. My wykorzystywaliśmy również kratki naszych zeszytów. Dlatego możemy powiedzieć, że narysowaliśmy zadane kąty, ale wcale ich nie skonstruowaliśmy. Jak skonstruować kąt o zadanej funkcji trygonometrycznej dowiemy się z animacji.

Słownik

skonstruować

w rozumieniu matematyki – narysować jedynie z wykorzystaniem cyrkla i linijki

kąt

obszar powstały z rozcięcia płaszczyzny przez sumę dwóch różnych półprostych o wspólnym początku, wraz z tymi półprostymi

funkcje trygonometryczne kąta ostrego

zależności między długościami boków w trójkącie prostokątnym, w którym jeden z kątów ma miarę $α$

Wprowadzenie

Animacja

Słownik