Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Obliczymy miarę kąta pomiędzy wysokościami sąsiednich ścian poprowadzonymi na tę samą krawędź boczną.

Rozwiązanie

Oznaczmy przez $a$ długość krawędzi tego ostrosłupa. Przekątna podstawy tego ostrosłupa ma długość $a\sqrt{2}$. Ściany boczne są trójkątami równobocznymi, więc wszystkie wysokości ścian bocznych mają długość $\frac{a\sqrt{3}}{2}$.

Zróbmy rysunek pomocniczy:

R13RimdEoTJfr

Ilustracja przedstawia ostrosłup prawidłowy czworokątny. Na rysunku zaznaczono dwie wysokości na dwóch sąsiadujących ścianach. Wysokości wychodzą z różnych wierzchołków podstawy, ale ich spodki są w jednym punkcie. W ostrosłupie zaznaczono przekątną jego podstawy,ma ona długość $a\sqrt{2}$, zaznaczone wysokości ścian bocznych mają długość $\frac{a\sqrt{3}}{2}$. Kąt pomiędzy tymi wysokościami podpisano literą alfa.

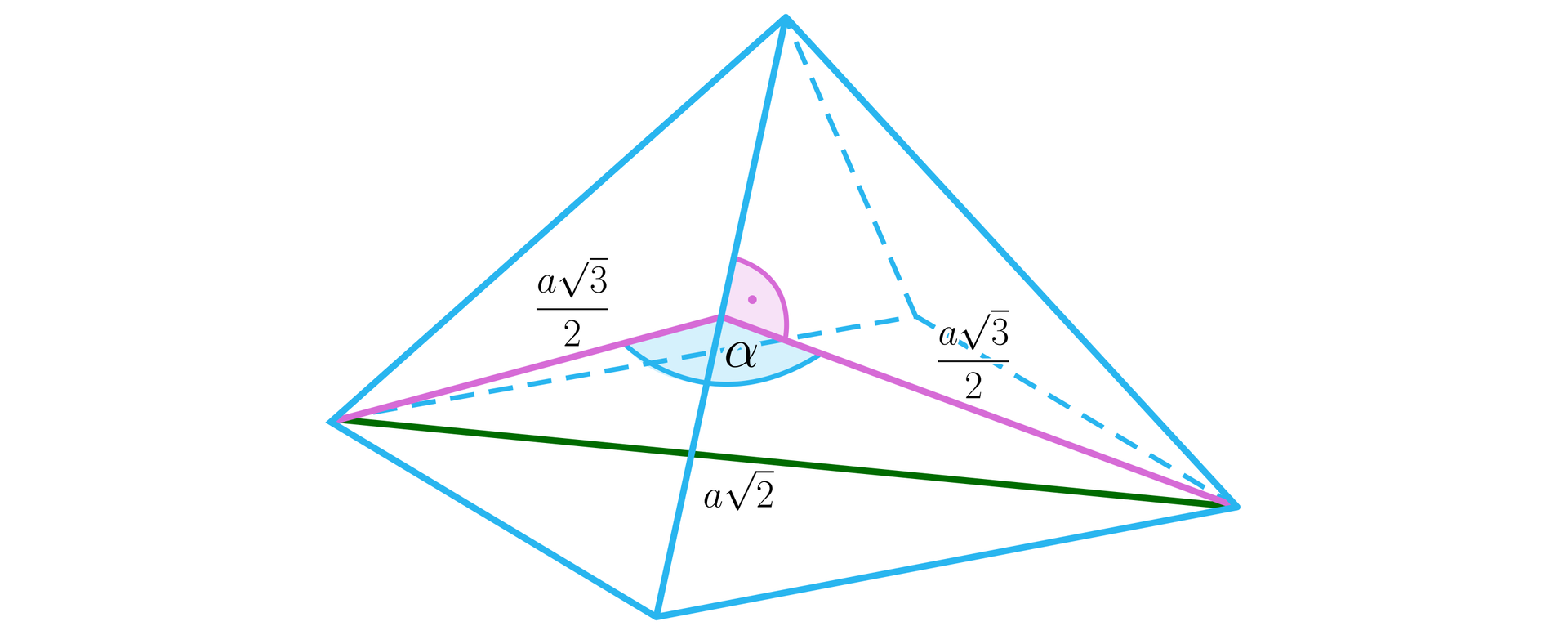
Z twierdzenia cosinusów mamy:

$2a^2=\frac{3a^2}{4}+\frac{3a^2}{4}-2·\frac{3a^2}{4}\cos \alpha$

$\frac{3a^2}{2}\cos \alpha =-\frac{a^2}{2}$

$\cos \alpha =-\frac{1}{3}$

Zatem: $\alpha \approx 180°-70°=110°$

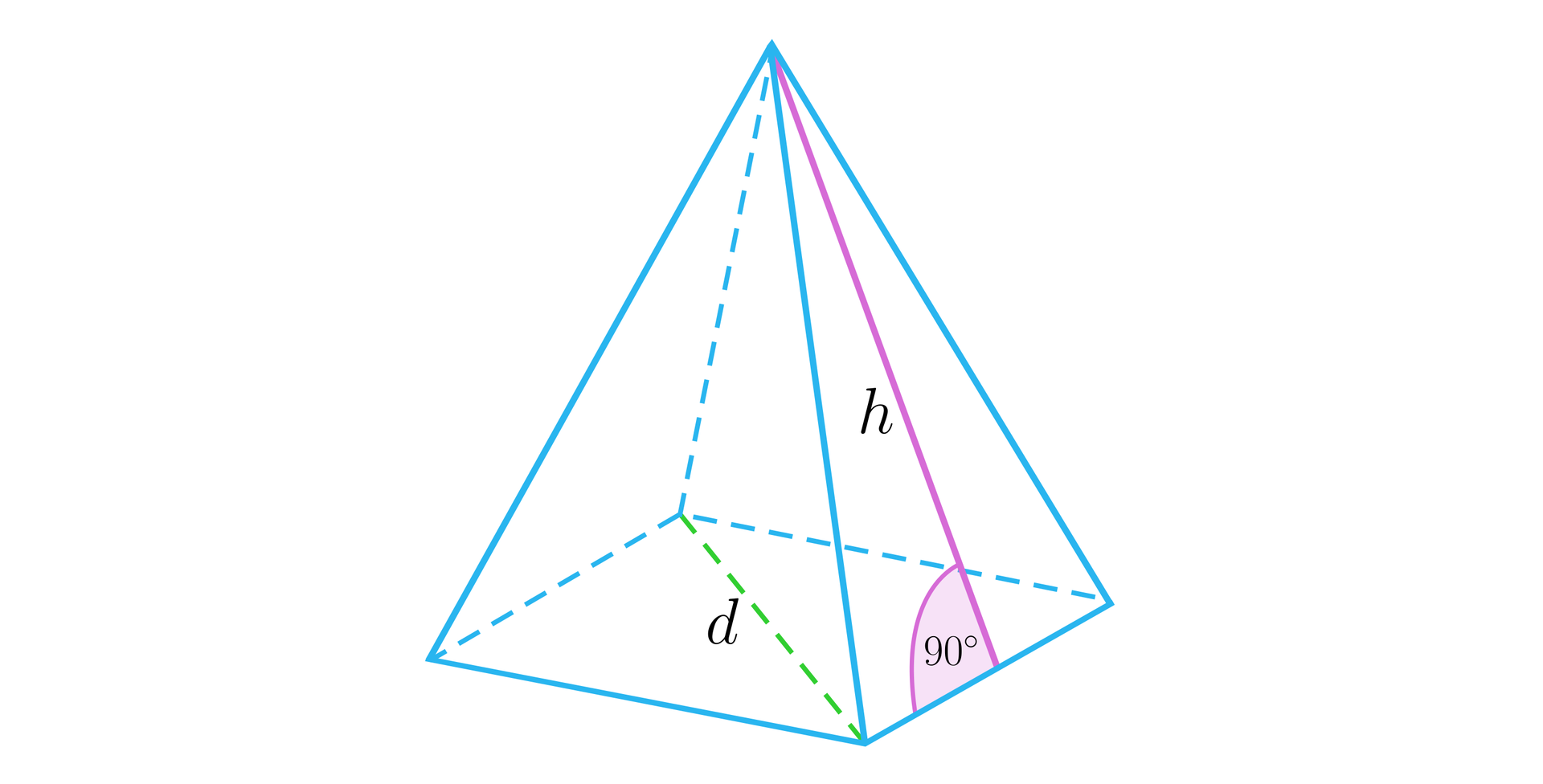
Obliczymy długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego  przedstawionego  na rysunku.

Rozwiązanie

RLQnDpWnQodQZ

Ilustracja przedstawia ostrosłup prawidłowy czworokątny A, B, C, D, E, F. Z wierzchołka E opuszczono wysokość na krawędź AB, spodek tej wysokości podpisano literą F. Odcinek EF ma długość sześć. Kąt nachylenia krawędzi bocznej BE do krawędzi podstawy AB ma miarę 72 stopni.

Ponieważ trójkąt $EFB$ jest prostokątny to $\frac{6}{\left|BE\right|}=\sin 72°$.

Czyli $\left|BE\right|=\frac{6}{\sin 72°}$.

Odczytujemy wartość sinusa z tabeli wartości funkcji trygonometrycznych i otrzymujemy długość krawędzi bocznej

$\left|BE\right|=\frac{6}{0,9511}\approx 6,31$

Obliczymy wysokość ostrosłupawysokość ostrosłupawysokość ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają długość $4$.

Rozwiązanie

R1DbaDIQBi9FH

Ilustracja przedstawia ostrosłup prawidłowy czworokątny. Na rysunku zaznaczono przekątne podstawy. W ostrosłupie zaznaczono trójkąt prostokątny, którego przeciwprostokątna to wysokość małe h ściany bocznej, przyprostokątnymi są wysokość ostrosłup a wielkie H i odcinek pomiędzy tymi wysokościami leżący w płaszczyźnie podstawy. Krawędź boczna ma długość cztery. Krawędź podstawy ma długość cztery, a odcinek pomiędzy wysokościami ma długość dwa.

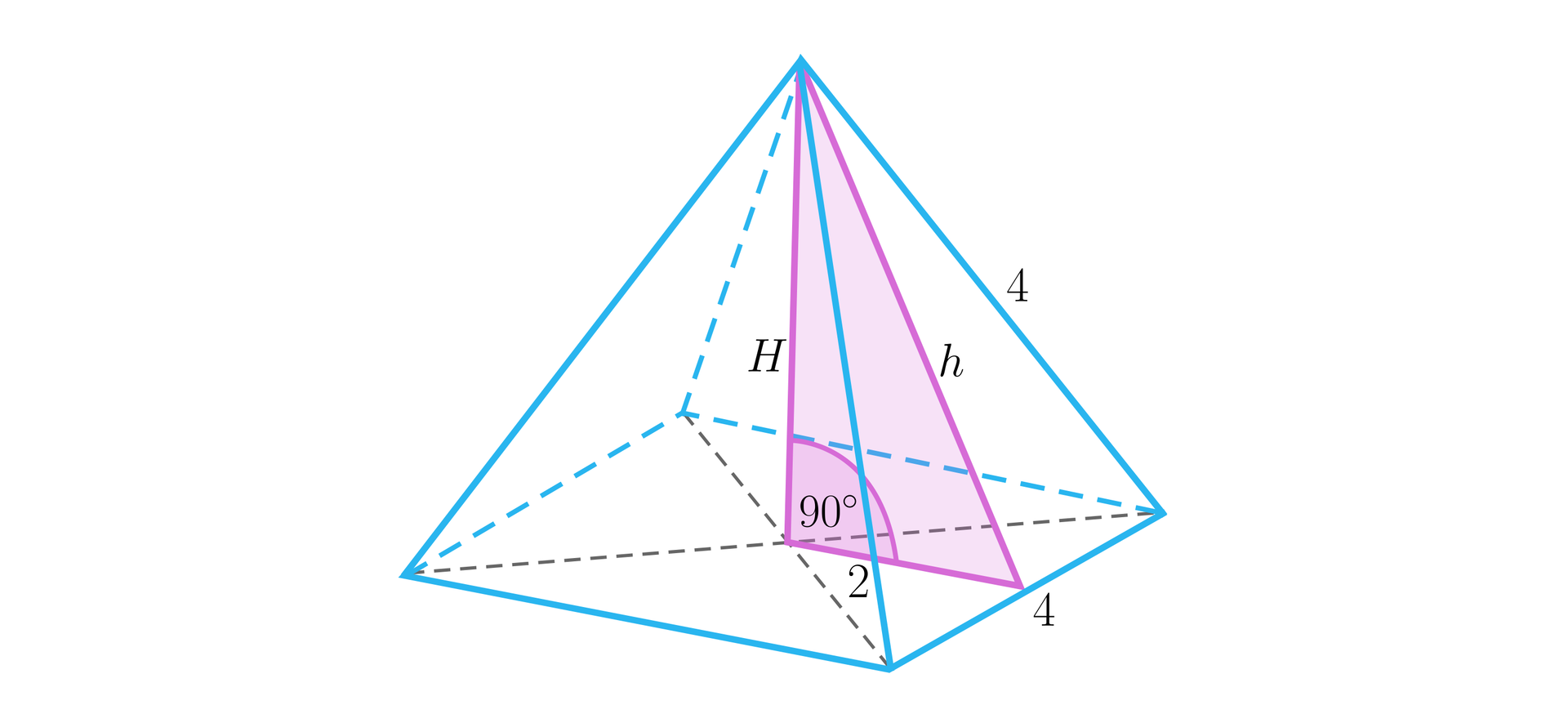
Ściana boczna tego ostrosłupa jest trójkątem równobocznym, a zatem

$h=\frac{4\sqrt{3}}{2}=2\sqrt{3}$

Obliczamy wysokość ostrosłupa korzystając z twierdzenia Pitagorasa

$H^2+2^2={\left(2\sqrt{3}\right)}^2$

$H^2+4=12$

$H^2=8$, a zatem $H=2\sqrt{2}$.

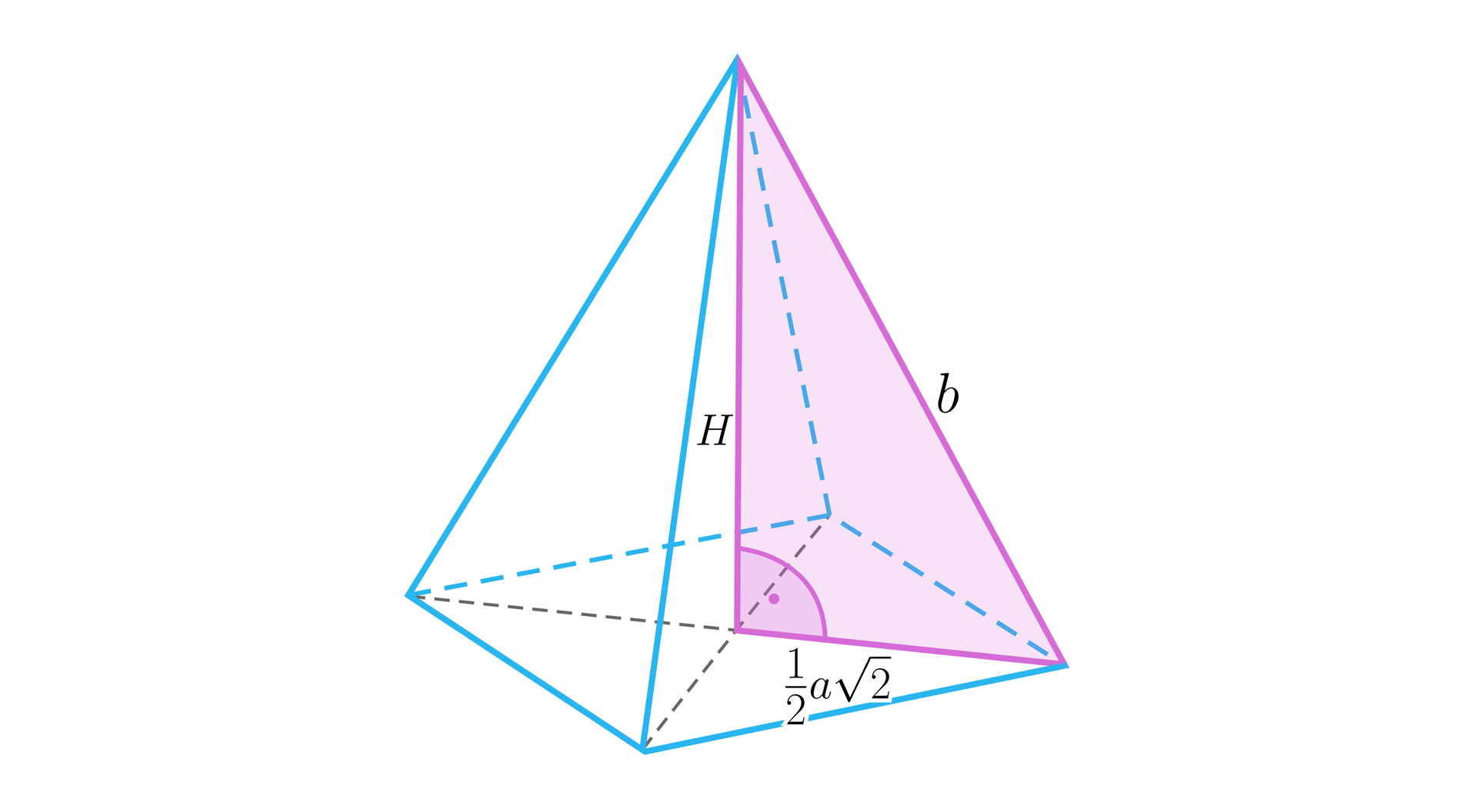
Obliczymy długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego o krawędzi podstawy $8$ i wysokości $12$.

Rozwiązanie

Obliczamy najpierw długość przekątnej podstawy $d=8\sqrt{2}$.

A zatem $\frac{1}{2}d=4\sqrt{2}$.

Korzystając z twierdzenia Pitagorasa otrzymujemy

${12}^2+{\left(4\sqrt{2}\right)}^2=b^2$

$144+32=b^2$

$176=b^2$, a stąd $b=4\sqrt{11}$.

Obliczymy, ile szkła trzeba zużyć na szklaną piramidę stojącą przed Luwrem.

Rozwiązanie

R1U9vNzjdeRCq

Ilustracja przedstawia ostrosłup prawidłowy czworokątny. W ostrosłupie zaznaczono trójkąt prostokątny, którego przeciwprostokątna to wysokość ściany bocznej h, przyprostokątnymi są wysokość ostrosłupa o długości 21 i odcinek łączący te wysokości o długości 17,5. Krawędź podstawy ma długość trzydzieści pięć.

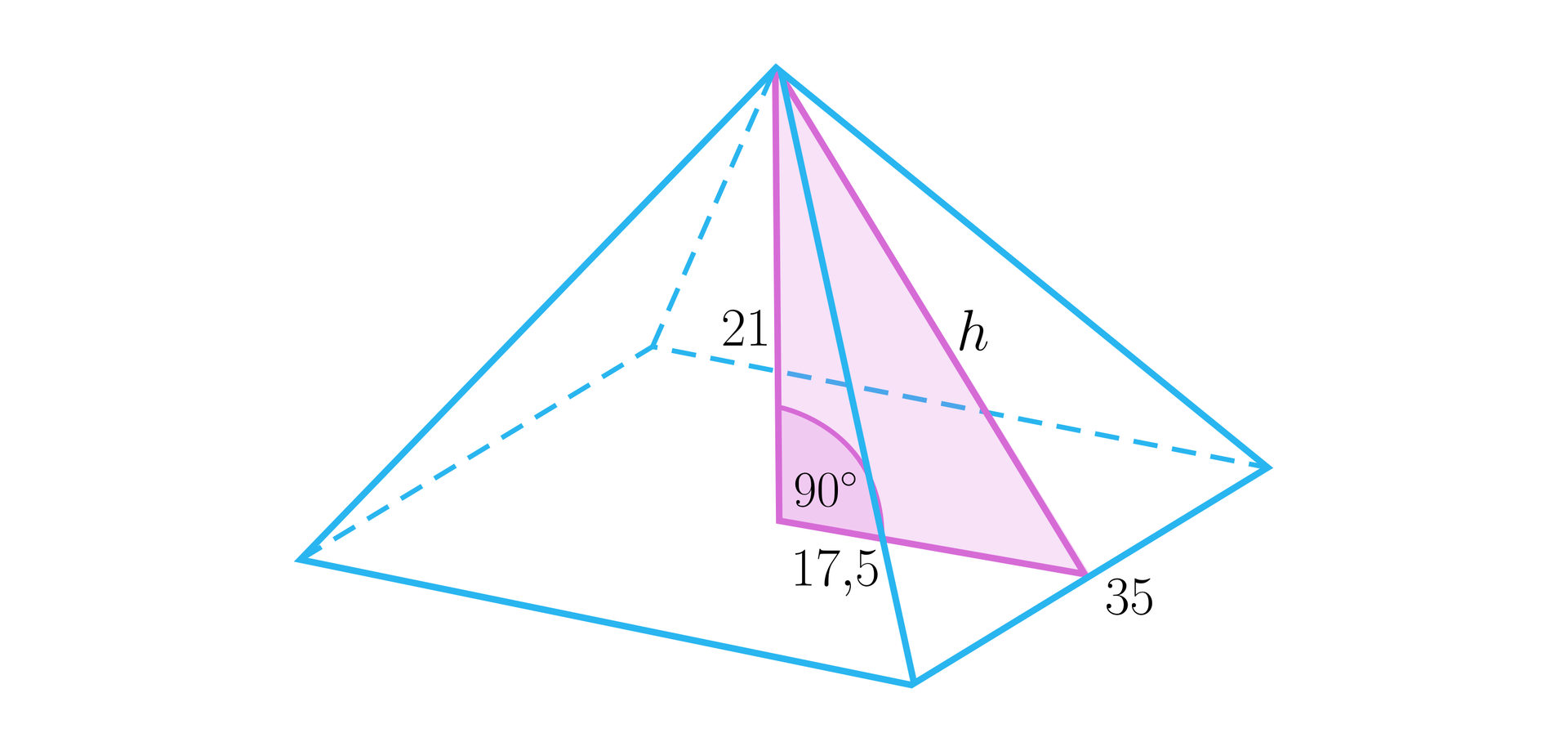
Korzystając z twierdzenia Pitagorasa obliczamy wysokość ściany bocznejwysokość ściany bocznejwysokość ściany bocznej

${21}^2+{\left(17,5\right)}^2=h^2$

$747,25=h^2$

Czyli $h\approx 27,3 \mathrm{m}$

Stąd $P=\frac{35·27,3}{2}=477,75 {\mathrm{m}}^2$

A zatem na wszystkie ściany zużyjemy ok. $477,75·4=1911 {\mathrm{m}}^2$ szkła.

Obliczymy odległość spodka wysokości ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości $8$ i wysokości długości $4$ od krawędzi bocznej.

Rozwiązanie

Zrobimy rysunek pomocniczy:

R1IJKbkCfvBVY

Ilustracja przedstawia ostrosłup prawidłowy czworokątny A, B, C, D, E. Krawędź podstawy ostrosłupa jest równa 8, a jego wysokość jest równa 4. Na rysunku zaznaczono trójkąt prostokąty E, B, S. Zaznaczono w nim jego wysokość FS. Punkt S leży na przecięciu przekątnych podstawy.

Trójkąt $BSE$ jest prostokątny oraz $\left|BS\right|=\frac{1}{2}·8\sqrt{2}=4\sqrt{2}$.

Obliczymy długość przeciwprostokątnej $BE$ tego trójkąta. Z Twierdzenia Pitagorasa mamy: ${\left(4\sqrt{2}\right)}^2+4^2={\left|BE\right|}^2$

Czyli $\left|BE\right|=\sqrt{48}=4\sqrt{3}$.

Obliczmy pole trójkąta $BSE$:

$P=\frac{1}{2}·4·4\sqrt{2}$

Odległość $SF$ spodka wysokości od krawędzi bocznej obliczymy korzystając z pola trójkąta $BSE$:

$P=\frac{1}{2}·4\sqrt{3}·\left|SF\right|$

$8\sqrt{2}=2\sqrt{3}·\left|SF\right|$

A stąd: $\left|SF\right|=\frac{8\sqrt{2}}{2\sqrt{3}}=\frac{4\sqrt{6}}{3}$.

W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość $6\sqrt{3}$, a wysokość ostrosłupa $6$. Obliczymy odległość spodka wysokości ostrosłupa od wysokości ściany bocznej poprowadzonej z wierzchołka ostrosłupa.

Rozwiązanie

Zrobimy rysunek pomocniczy

R8chwvRg9sBKn

Ilustracja przedstawia ostrosłup prawidłowy czworokątny A, B, C, D, E. W ostrosłupie zaznaczono przekrój trójkąta prostokątnego E, G, S. Odcinek ES jest wysokością ostrosłupa , wysokością ściany bocznej jest EG. Kąt ESG jest kątem prostym. W trójkącie zaznaczono jego wysokość HS. Punkt S leży na przecięciu przekątnych podstawy.

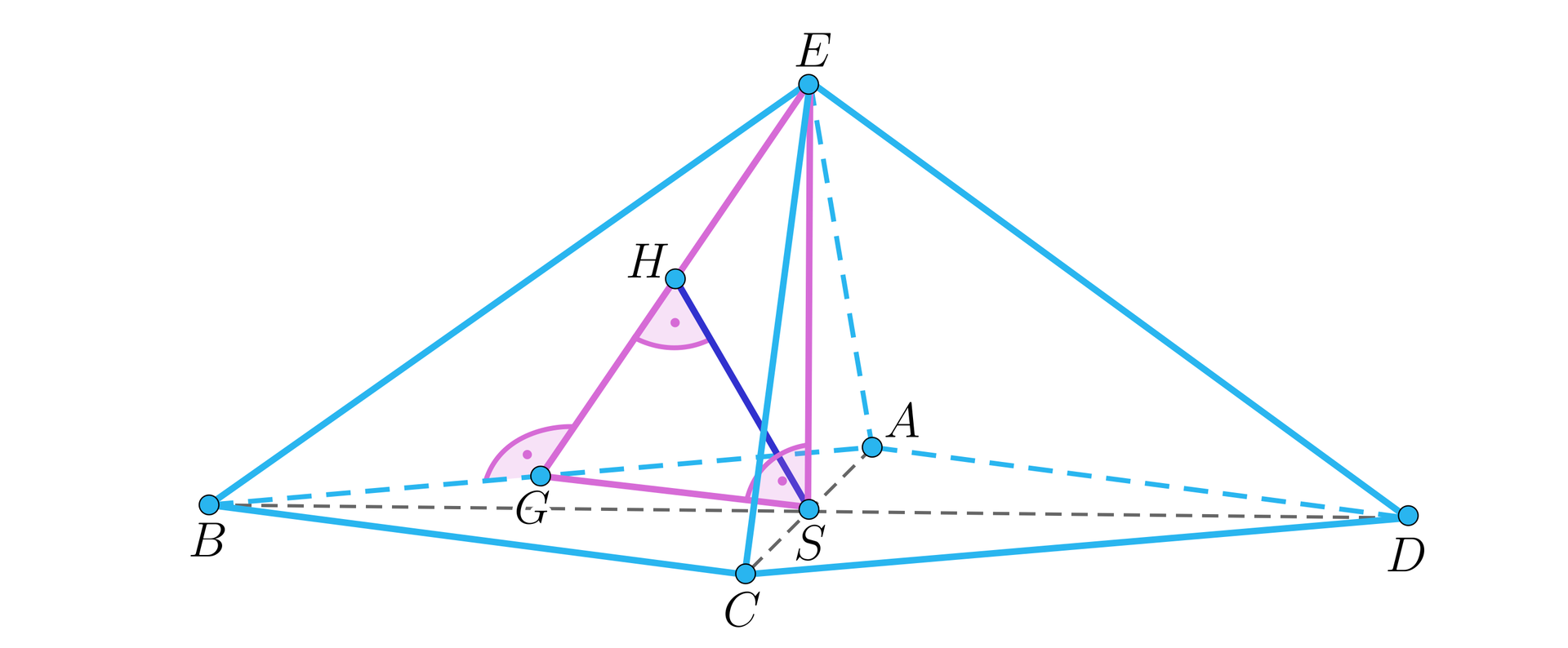
Zgodnie z danymi z treści zadania $\left|BE\right|=6\sqrt{3}$ i $\left|SE\right|=6$.

Obliczymy długość krawędzi podstawy tego ostrosłupa. Najpierw obliczmy długość odcinka $BS$ z twierdzenia Pitagorasa:

${\left|BS\right|}^2+6^2={\left(6\sqrt{3}\right)}^2$.

Zatem: $\left|BS\right|=6\sqrt{2}$.

Krawędź podstawy ma długość $\left|BA\right|=12$ (odcinek $BS$ to połowa przekątnej podstawy).

Mamy więc: $\left|GS\right|=\frac{1}{2}·\left|BA\right|=6$

Trójkąt $GSE$ jest więc prostokątny i równoramienny, czyli $\left|EG\right|=6\sqrt{2}$ i $\left|SH\right|=3\sqrt{2}$.

A zatem odległość spodka wysokości ostrosłupa od wysokości ściany bocznej opuszczonej na krawędź podstawy wynosi $3\sqrt{2}$.

bok wielokąta znajdującego się w podstawie ostrosłupa

przekątna wielokąta znajdującego się w podstawie ostrosłupa

odcinek łączący wierzchołek podstawy z wierzchołkiem ostrosłupa

najkrótszy odcinek łączący wierzchołek ostrosłupa z płaszczyzną podstawy

wysokość trójkąta równoramiennego będącego ścianą boczną poprowadzona z wierzchołka ostrosłupa na krawędź podstawy