Przeczytaj
Tabela danych w arkuszu kalkulacyjnym jest dynamicznym zakresem danych umożliwiającym wykonywanie dowolnych obliczeń w oparciu o jedną lub dwie komórki wejściowe (jedną lub dwie zmienne). Dzięki temu narzędziu możemy wykonać symulacjęsymulację wielu rozwiązań dla danej formuły.
Przykładem wykorzystania Tabeli danych dla jednej zmiennej może być kalkulator liczący wysokość raty kredytu w zależności od wysokości oprocentowania.
Zmienną, w oparciu o którą będzie tworzona Tabela danych, jest wysokość oprocentowania. Pozostałe dane występujące w kalkulatorze to: kwota pożyczki, częstotliwość spłat rat (w tym przypadku jest to częstotliwość miesięczna) oraz okres kredytowania.
Microsoft Excel
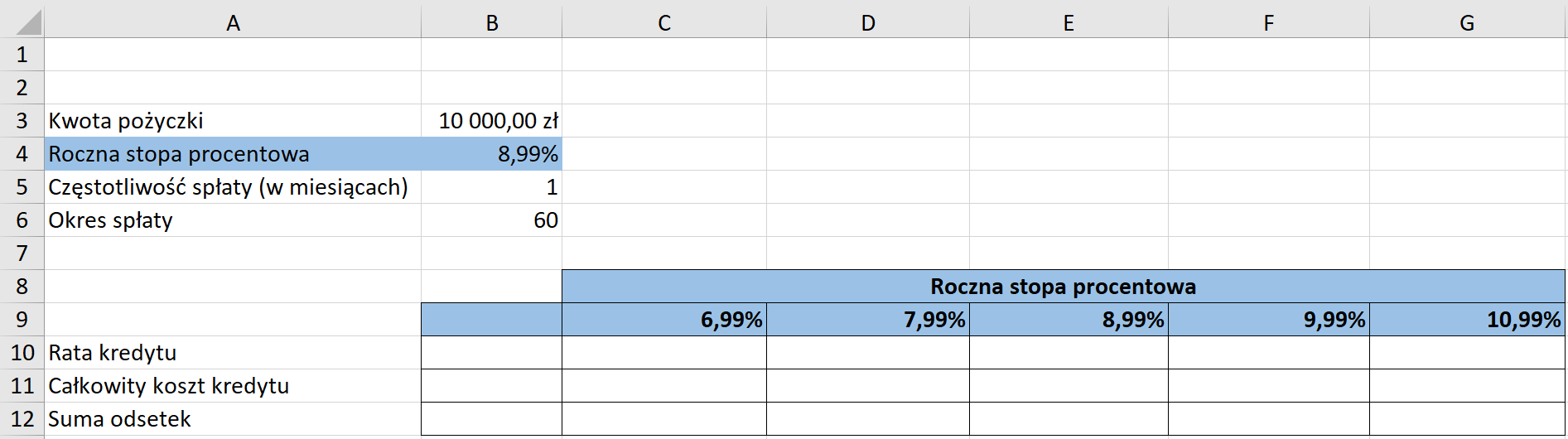
Zanim przejdziemy do tworzenia Tabeli danych należy zdefiniować odpowiednie formuły do poszczególnych obliczeń.
Do obliczenia wysokości raty możemy wykorzystać funkcję PMT, czyli gotową w arkuszu kalkulacyjnym formułę finansową służącą do wyliczania rat kredytu dla stałego oprocentowania:
=-PMT(B4/12;B6;B3)
gdzie:
pierwszy argument oznacza wysokość oprocentowania w badanym okresie (w tym przypadku obliczamy ratę miesięczną, a więc wysokość rocznego oprocentowania w komórce
B4należy podzielić przez 12 miesięcy);drugi argument oznacza liczbę miesięcy spłaty kredytu;
trzeci argument oznacza kwotę pożyczki.
Formuła licząca całkowity koszt kredytu to nic innego jak wysokość miesięcznej raty pomnożona przez liczbę rat, a więc:
=B10*B6,
natomiast suma odsetek to różnica pomiędzy całkowitym kosztem kredytu a kwotą pożyczki, czyli:
=B11‑B3.
Funkcja PMT automatycznie zwraca ujemną wartość wysokości raty, stąd też należy pamiętać, aby poprzedzić ją znakiem minus („-”) w celu uzyskania w wyniku dodatniej wartości.
W rezultacie otrzymujemy następujące wyniki.
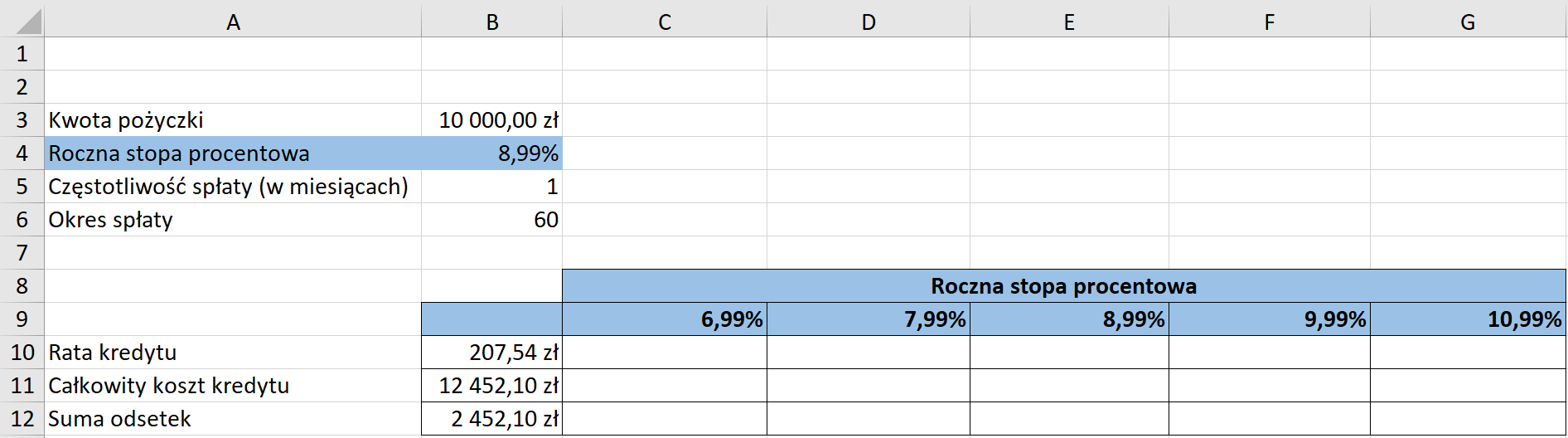
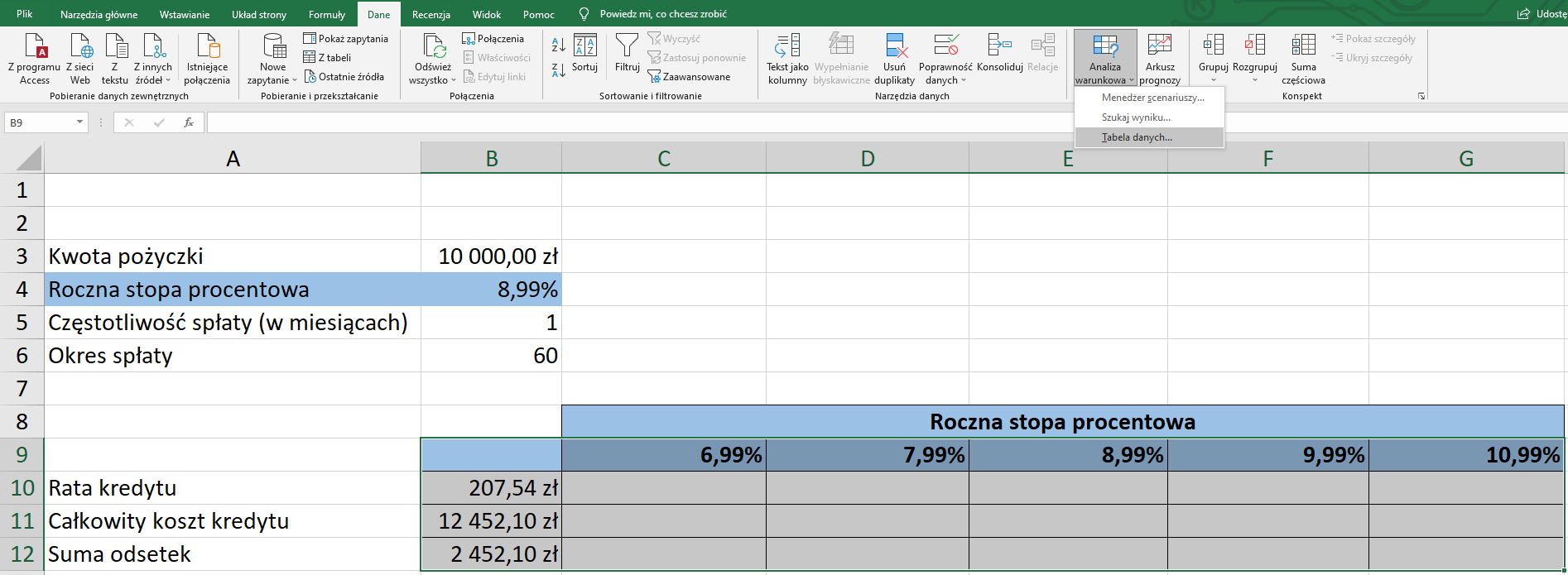
Teraz możemy przejść do tworzenia Tabeli danych. W tym celu zaznaczamy obszar danych, który będzie analizowany, tj. zakres B9:G12, następnie ze wstążki wybieramy zakładkę Dane, w obszarze Prognoza wybieramy Analiza warunkowa, a z listy rozwijalnej wybieramy Tabela danych.
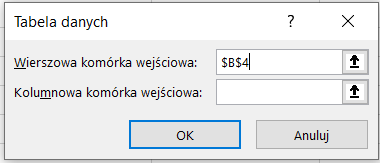
Pojawia się wówczas okno Tabela danych, w którym definiujemy zmienne wejściowe. W naszym przykładzie mamy tylko jedną zmienną – roczną stopę procentową, więc jako Wierszową komórkę wejściową definiujemy komórkę B4.
Po zatwierdzeniu przyciskiem OK otrzymujemy Tabelę danych, dzięki której możemy rozważyć kilka scenariuszyscenariuszy kosztów kredytu w zależności od zastosowanego oprocentowania.
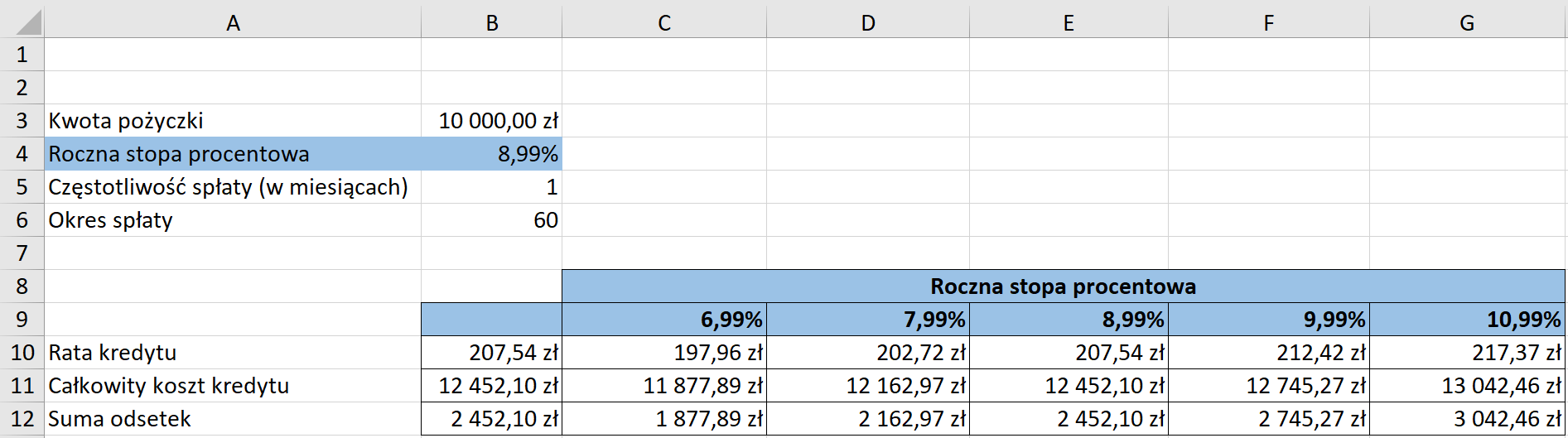
Warto pamiętać również o tym, że narzędzie Tabela danych daje możliwość poznania wyników także dla innych wartości wejściowych. W tym celu nie musimy tworzyć kolejnych kolumn z kolejnymi wartościami oprocentowania. Wystarczy zmienić wysokość oprocentowania w dostępnej tabeli, a arkusz kalkulacyjny automatycznie przeliczy poszczególne parametry dla nowej wartości.
Z kolei przykładem wykorzystania tego narzędzia dla dwóch zmiennych może być stworzenie kalkulatora, dzięki któremu można przeprowadzić symulację scenariuszy, jaki zysk z lokaty może uzyskać klient banku w zależności od wysokości jej oprocentowania oraz zainwestowanej kwoty.
Załóżmy, że klient dysponuje wolnymi środkami w wysokości 10 000 – 30 000 zł, które chciałby zainwestować na najbliższe 3 lata i ma do wyboru trzy lokaty z różnym oprocentowaniem (2%, 3% oraz 4,5% w skali roku). W przypadku każdej z tych lokat mamy do czynienia z kwartalną kapitalizacją odsetek.
Aby stworzyć taką tabelę danych, na początek należy zdefiniować dwie zmienne. W naszym przykładzie pierwszą zmienną będzie wysokość zainwestowanej kwoty, a drugą wysokość oprocentowania w skali roku. Następnie tworzymy formułę, która ma być obliczana w oparciu o te dwie zmienne. W tym przypadku do wyliczenia zysku z lokaty z uwzględnieniem kapitalizacji odsetek możemy wykorzystać jedną z funkcji finansowych, mianowicie funkcję FV.
Będzie ona wyglądała w następujący sposób:
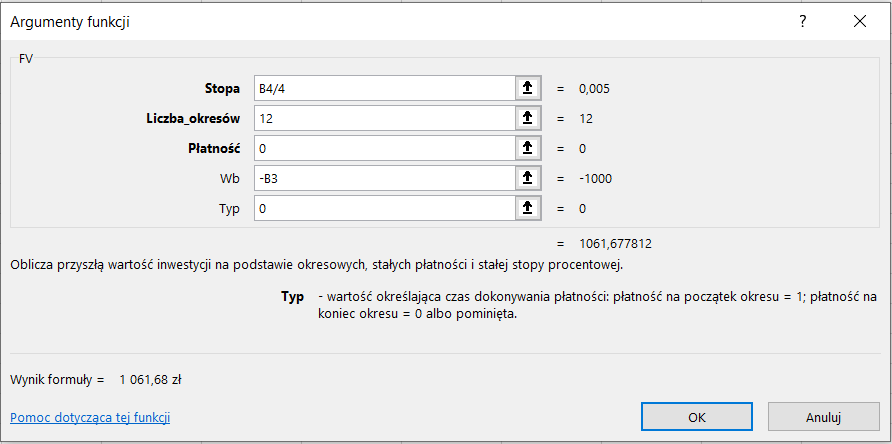
gdzie poszczególne argumenty funkcji to:
Stopa– stopa procentowa dla badanego okresu kapitalizacji odsetek (np. w przypadku kapitalizacji miesięcznej roczna stopa procentowa musi być podzielona przez 12, w przypadku kapitalizacji kwartalnej przez 4 itd.);Liczba_okresów– liczba okresów, w których następuje kapitalizacja odsetek (ponieważ w rozpatrywanym przypadku mamy do czynienia z lokatą zawieraną na 3 lata, a kapitalizacja odsetek odbywa się co 3 miesiące, to łączna liczba kapitalizacji wynosić będzie 12);Płatność– domyślnie wpisujemy „0”, co oznacza, że płatność odsetek odbywa się w równych odstępach czasowych;Wb– początkowa wysokość zainwestowanej kwoty (poprzedzona znakiem „-”, aby ostateczny wynik nie był ujemny);Typ– domyślnie wpisujemy „0”, co oznacza, że kapitalizacja odbywa się na koniec każdego okresu.
Warto pamiętać o tym, że funkcja FV zwraca całkowitą wartość inwestycji, a więc kwotę początkową wraz z wygenerowanym zyskiem. W naszym zadaniu interesuje nas sam zysk, więc dodatkowo od wartości uzyskanej dzięki funkcji FV odejmujemy wartość początkową lokaty, tak więc formuła wyglądać będzie następująco:
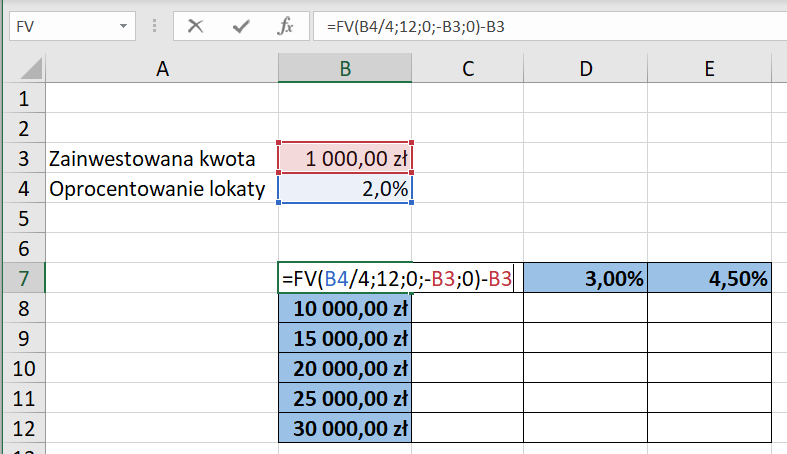
Następnie zaznaczamy całą tabelę, a więc obszar B7:E12 i ze wstążki wybieramy zakładkę Dane, w obszarze Prognoza wybieramy Analiza warunkowa, a z rozwiniętej listy wybieramy Tabela danych. W oknie Tabela danych definiujemy nasze zmienne wejściowe. Wierszową komórką wejściową będzie oprocentowanie lokaty, a więc komórka B4, a Kolumnową komórką wejściową będzie zainwestowana kwota, czyli komórka B3.
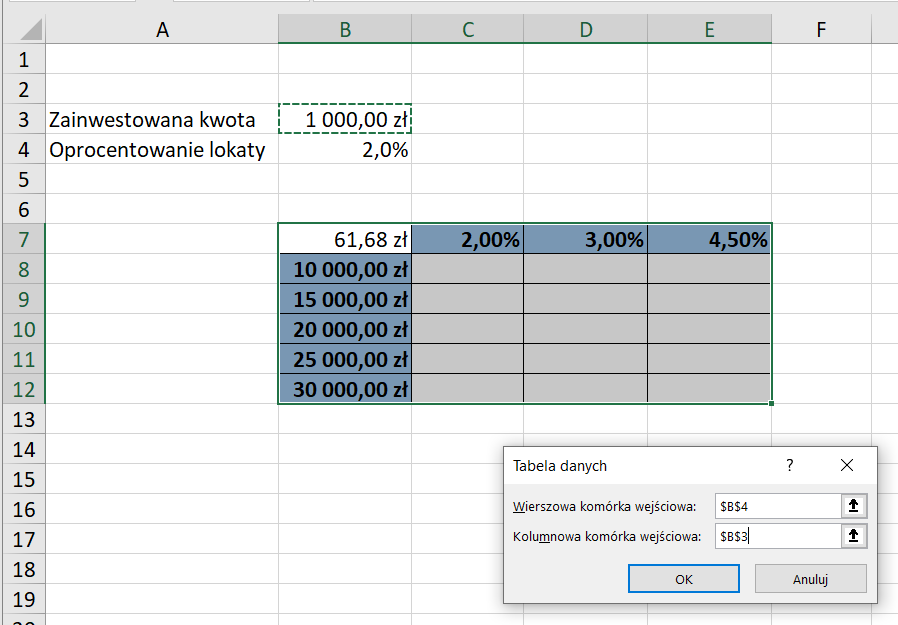
Całość zatwierdzamy przyciskiem OK. Dzięki narzędziu Tablica danych arkusz kalkulacyjny rozpatrzył wszystkie możliwe scenariusze dla poszczególnych wartości w rezultacie otrzymując gotowe zestawienie zysku z 3‑letniej lokaty w zależności od zainwestowanej kwoty i wysokości oprocentowania.
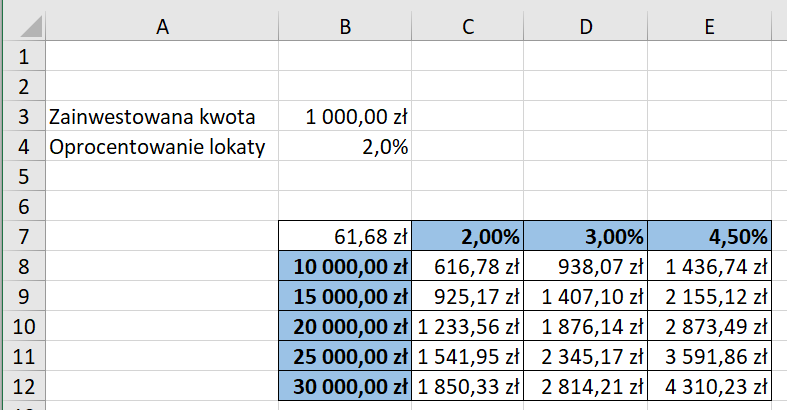
W przypadku, gdyby interesowało nas poznanie, jak będzie wyglądał zysk z lokaty o innej wartości lub o innym oprocentowaniu, wystarczy zmienić odpowiednio dane w kolumnowych lub wierszowych komórkach wejściowych.
LibreOffice Calc
LibreOffice Calc nie posiada narzędzia do tworzenia tabeli danych, tabelę będziemy musieli wypełnić ręcznie.
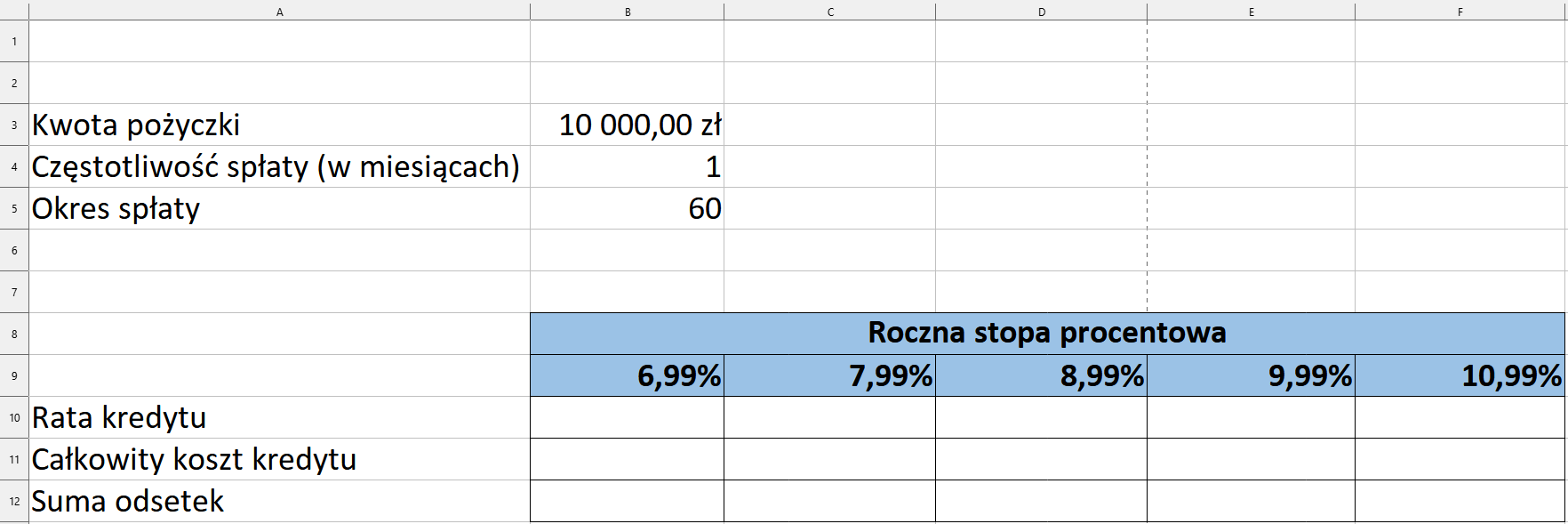
Do obliczenia wysokości raty możemy wykorzystać funkcję PMT, czyli gotową w arkuszu kalkulacyjnym formułę finansową służącą do wyliczania rat kredytu dla stałego oprocentowania. Do komórki B10 wprowadzimy formułę:
gdzie:
pierwszy argument oznacza wysokość oprocentowania w badanym okresie (w tym przypadku obliczamy ratę miesięczną, a więc wysokość rocznego oprocentowania w komórce
B9należy podzielić przez 12 miesięcy);drugi argument oznacza liczbę miesięcy spłaty kredytu;
trzeci argument oznacza kwotę pożyczki.
Formuła licząca całkowity koszt kredytu to nic innego jak wysokość miesięcznej raty pomnożona przez liczbę rat, a więc w komórce B11 znajdzie się formuła:
=B10*$B$5,
natomiast suma odsetek to różnica pomiędzy całkowitym kosztem kredytu a kwotą pożyczki, czyli w komórce B12 znajdzie się formuła:
=B11-$B$3.
Funkcja PMT automatycznie zwraca ujemną wartość wysokości raty, stąd też należy pamiętać, aby poprzedzić ją znakiem minus („-”) w celu uzyskania w wyniku dodatniej wartości.
W rezultacie otrzymujemy następujące wyniki.
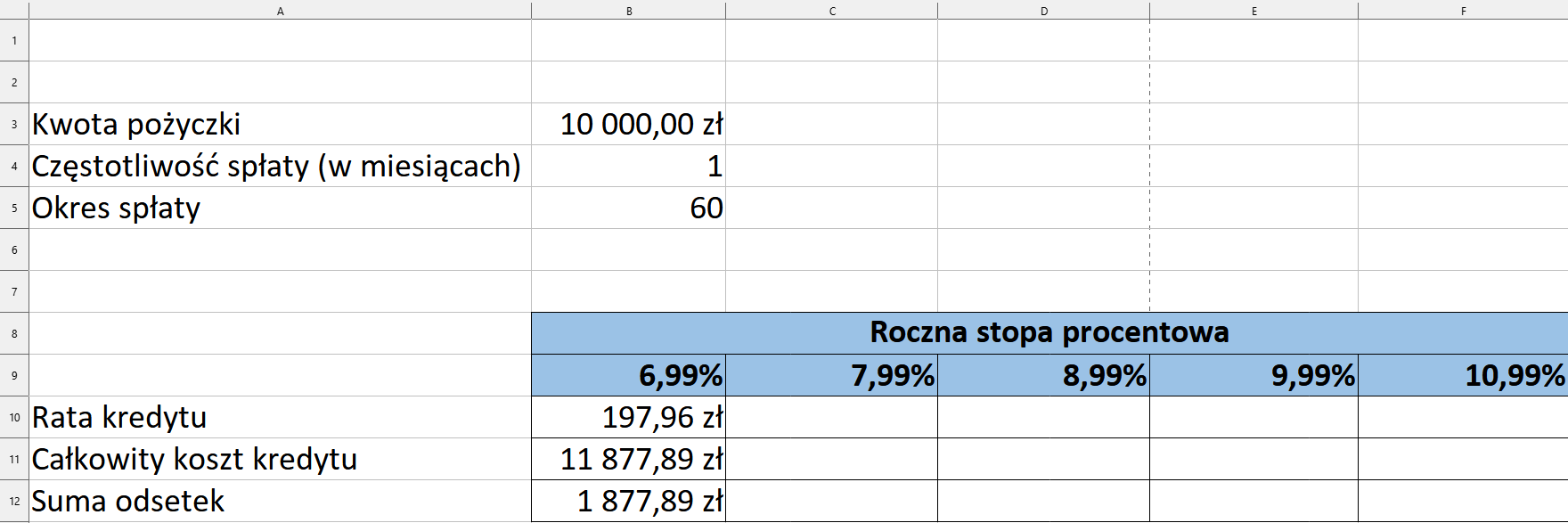
Każdą z wpisanych formuł skopiujmy w prawo aż do kolumny F.
W rezultacie otrzymujemy następujące wyniki.
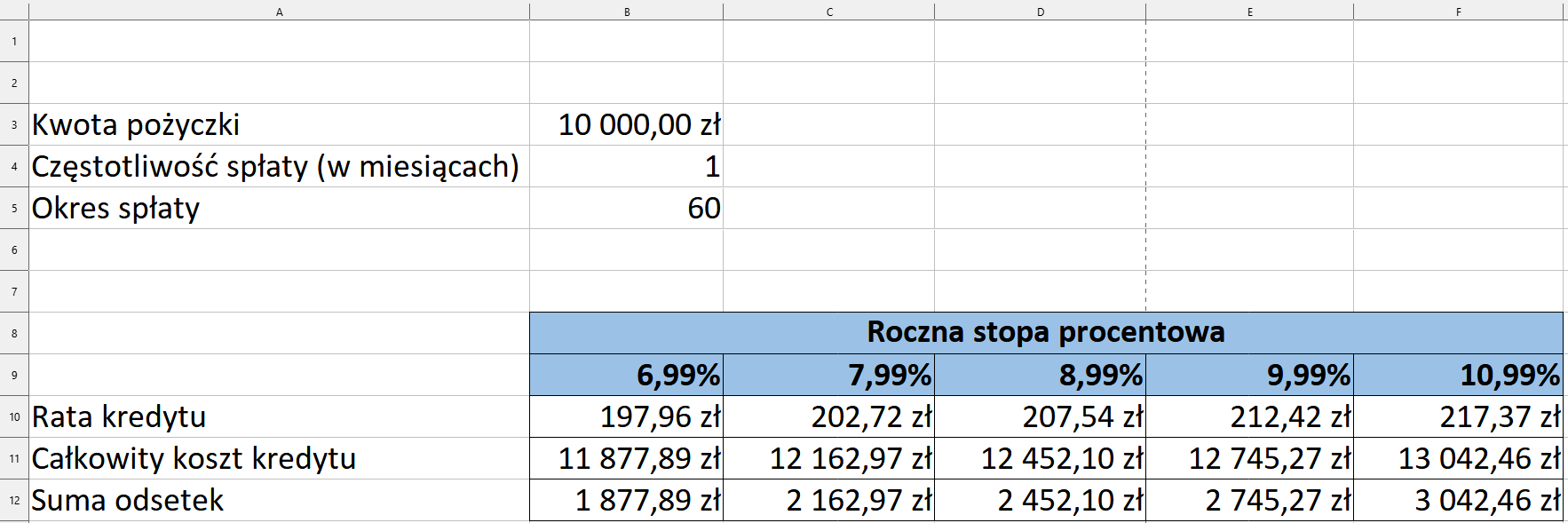
W tabeli możemy zobaczyć, jak zmienia się rata kredytu, całkowity jego koszt a także suma odsetek w zależności od oprocentowania.
Podobnie zadziałamy w przypadku drugiego przykładu. Stwórzmy kalkulator, dzięki któremu można przeprowadzić symulację scenariuszy, jaki zysk z lokaty może uzyskać klient banku w zależności od wysokości jej oprocentowania oraz zainwestowanej kwoty.
Załóżmy, że klient dysponuje wolnymi środkami w wysokości 10 000 – 30 000 zł, które chciałby zainwestować na najbliższe 3 lata i ma do wyboru trzy lokaty z różnym oprocentowaniem (2%, 3% oraz 4,5% w skali roku). W przypadku każdej z tych lokat mamy do czynienia z kwartalną kapitalizacją odsetek.
W tym przypadku do wyliczenia zysku z lokaty z uwzględnieniem kapitalizacji odsetek możemy wykorzystać jedną z funkcji finansowych, mianowicie funkcję FV.
Będzie ona wyglądała w następujący sposób:
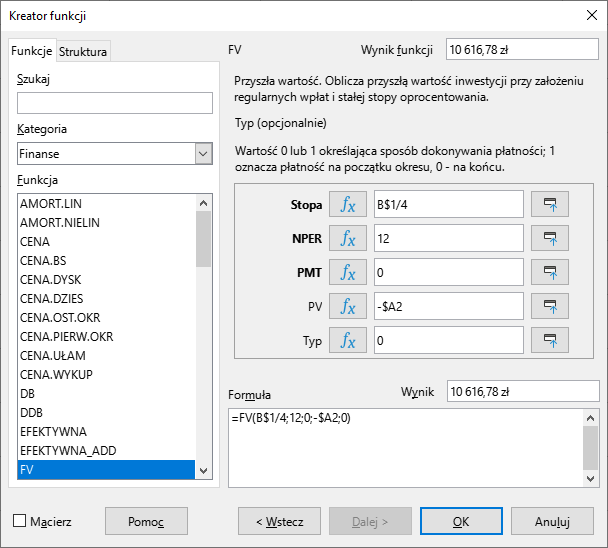
gdzie poszczególne argumenty funkcji to:
Stopa– stopa procentowa dla badanego okresu kapitalizacji odsetek (np. w przypadku kapitalizacji miesięcznej roczna stopa procentowa musi być podzielona przez 12, w przypadku kapitalizacji kwartalnej przez 4 itd.);NPER– liczba okresów, w których następuje kapitalizacja odsetek (ponieważ w rozpatrywanym przypadku mamy do czynienia z lokatą zawieraną na 3 lata, a kapitalizacja odsetek odbywa się co 3 miesiące, to łączna liczba kapitalizacji wynosić będzie 12);PMT– domyślnie wpisujemy „0”, co oznacza, że płatność odsetek odbywa się w równych odstępach czasowych;PV– początkowa wysokość zainwestowanej kwoty (poprzedzona znakiem „-”, aby ostateczny wynik nie był ujemny);Typ– domyślnie wpisujemy „0”, co oznacza, że kapitalizacja odbywa się na koniec każdego okresu.
Warto pamiętać o tym, że funkcja FV zwraca całkowitą wartość inwestycji, a więc kwotę początkową wraz z wygenerowanym zyskiem. W naszym zadaniu interesuje nas sam zysk, więc dodatkowo od wartości uzyskanej dzięki funkcji FV odejmujemy wartość początkową lokaty, tak więc formuła wyglądać będzie następująco:
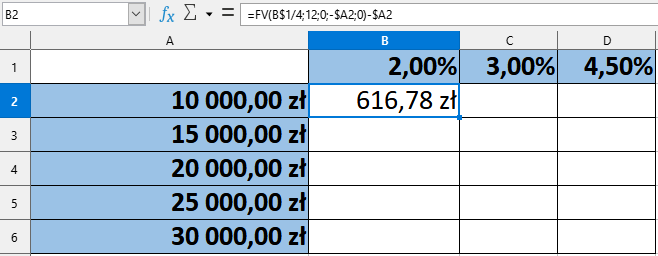
Skopiujmy ją do pozostałych komórek z zakresu B2:D6. W rezultacie otrzymaliśmy gotowe zestawienie zysku z danej lokaty w zależności od zainwestowanej kwoty.
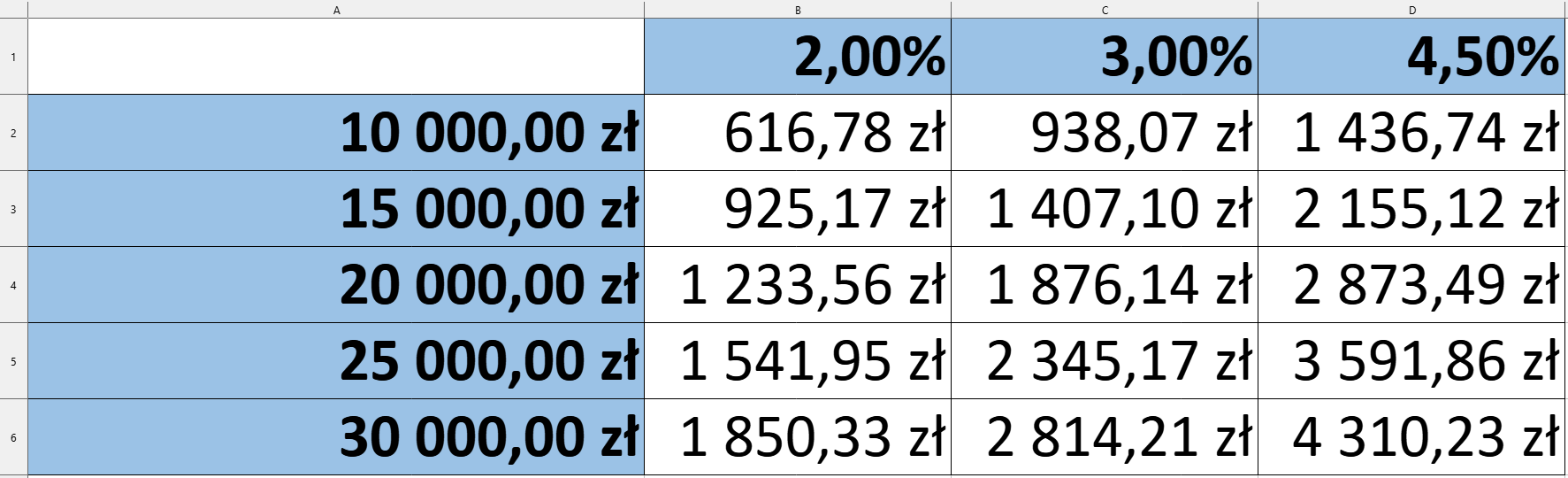
W przypadku, gdyby interesowało nas poznanie, jak będzie wyglądał zysk z lokaty o innej wartości lub o innym oprocentowaniu, wystarczy zmienić odpowiednio dane w kolumnowych lub wierszowych komórkach wejściowych.
Słownik
zestaw wartości, który zapisany w tabeli arkusza kalkulacyjnego może być dynamicznie podstawiany do wskazanych komórek w celu użycia tych wartości jako argumentów formuł liczących. Zastosowanie wielu scenariuszy daje możliwość dynamicznego porównania wyników dla poszczególnych zestawów danych bez konieczności wielokrotnego kopiowania formuł (lub skoroszytów)
sztuczne odtwarzanie właściwości danego obiektu lub zjawiska za pomocą jego modelu