Elektryczność

Przed zapoznaniem się z podstawowymi wielkościami związanymi z elektroniką przypomnijmy sobie, jak zbudowany jest atom. Atom składa się z cząstek elementarnych (subatomowych), takich jak: protony, neutrony oraz elektrony. Protony mają ładunek elektryczny dodatni i razem z elektrycznie obojętnymi neutronami wchodzą w skład jądra atomowego. Wokół jądra krążą z kolei elektrony, które mają ładunek ujemny.

R1RzObh0LvYhf

Na rysunku schemat atomu. Składa się z dwóch okręgów, narysowanych jeden w drugim w niewielkiej odległości. W centralnej części atomu znajdują się 4 czerwone koła oznaczone jako neutrony oraz cztery niebieskie koła ze znakiem plus, oznaczone jako protony. Neutrony i protony stanowią jądro atomu. Na krawędziach zewnętrznych okręgów oznaczono elektrony, małe zielone koła ze znakiem minus. W schemacie tego atomu znajdują się cztery elektrony. Trzy z nich znajdują się na wewnętrznym okręgu, jeden na zewnętrznym.

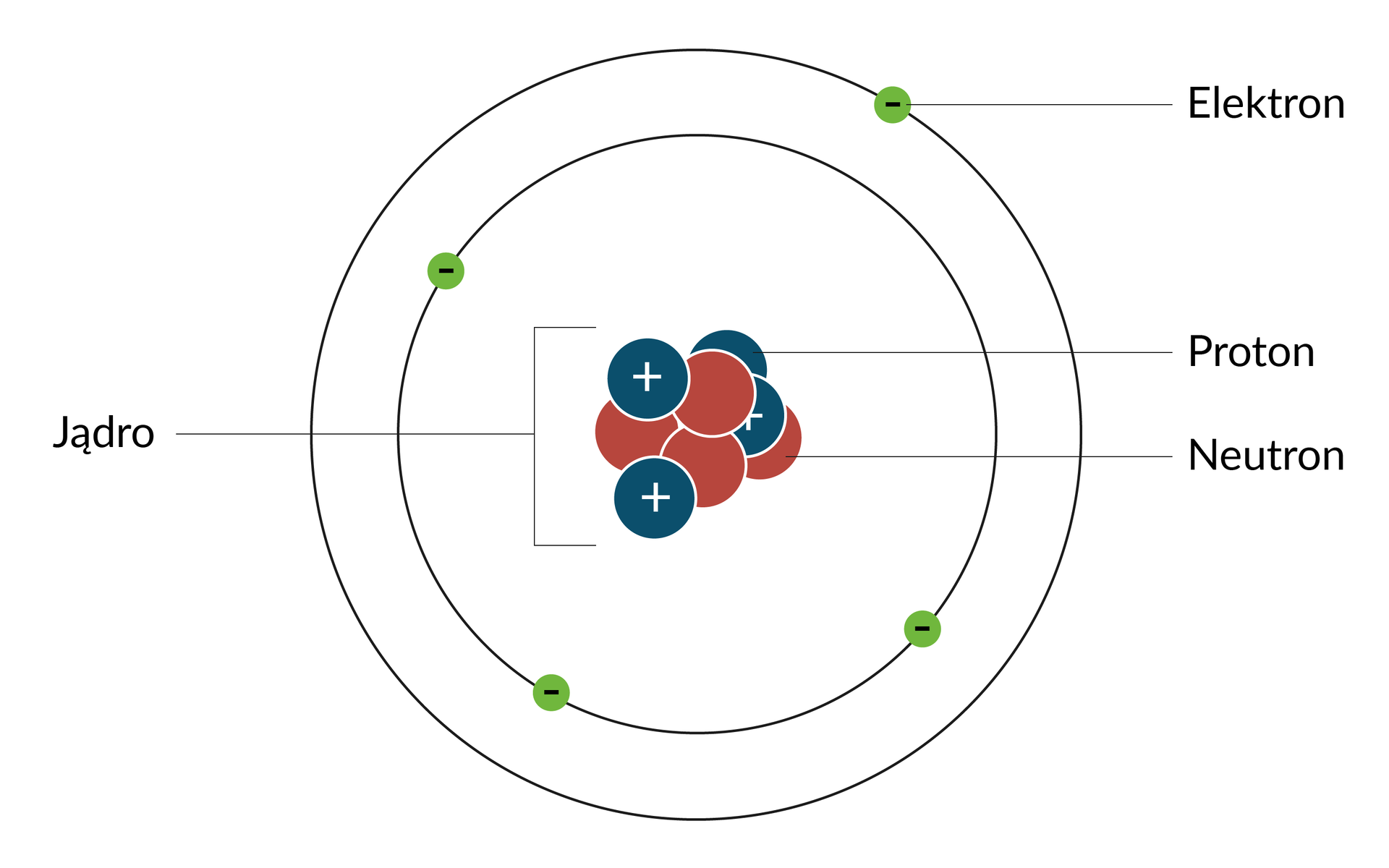
W pewnych warunkach zdarza się, że elektron oderwie się od „swojego” atomu i przeskoczy do innego. Atom, który stracił elektron, będzie miał od tej chwili ładunek dodatni, a atom, który zyskał elektron, będzie miał ładunek ujemny. Przepływ tych elektronów nazywamy elektrycznością.

Napięcie

Napięcie to siła, która wprawia w ruch elektrony. Powstaje ono, jeżeli w jednym punkcie jest więcej naładowanych cząstek niż w drugim. Często ta różnica liczby cząstek naładowanych nazywana jest różnicą potencjałów, czyli właśnie napięciem.

Napięcie można porównać do ciśnienia wody w rurze wodociągowej. Im ciśnienie jest większe, tym szybciej woda przepłynie przez rurę. Podobnie jest z napięciem - im jest ono wyższe, tym szybciej elektrony się przemieszczają.

Napięcie jest mierzone w woltach. Symbolem wolta jest litera V. Rozróżniamy dwa typy napięcia: napięcie zmienne oraz napięcie stałe. Napięcie zmienne spotkamy w  gniazdkach elektrycznych. Doprowadzane jest ono do domów z elektrowni, która takie napięcie wytwarza. My zajmiemy się napięciem stałym.

Napięcie stałe to napięcie wymuszające ruch elektronów tylko w jednym kierunku.  Źródłem napięcia stałego są popularne baterie „paluszki”, baterie 9 V, akumulatory lub zasilacze, które przekształcają napięcie przemienne w stałe.

Prąd

Przepływ naładowanych cząstek (elektronów) w obwodzie elektrycznym nazywamy prądem elektrycznym. Jednostką charakteryzującą wielkość prądu jest natężenie. Mierzy się je w amperach, których symbolem jest litera A. Umownie przyjmuje się że prąd płynie od punktu o wyższym potencjale do punktu o potencjale niższym. Potocznie używa się określenia „od plusa (+) do minusa (-)”.  Aby natężenie prądu mierzonego w pewnym punkcie obwodu wynosiło 1 A, musi w nim przepłynąć 6,241 ⋅ 10Indeks górny 18¹⁸ elektronów na sekundę.

Przykładowo, dioda LED pobiera prąd rzędu 20 mA (miliamperów) czyli 0,02 A (ampera). Silnik DCsilnik DCSilnik DC może pobrać nawet 2 A lub więcej, oczywiście w zależności od jego mocy.

Opór

Opór, często nazywany rezystancją, mówi, jak bardzo przepływ prądu jest ograniczany lub utrudniany. Każdy element obwodu elektronicznego ma własną rezystancję. W niektórych przypadkach jest ona bardzo mała. Dotyczy to np. przewodów: mają one pozwolić przepływać prądowi swobodnie. Jednak w elektronice bardzo często musimy zmniejszyć natężenie prądu. W tym celu wykorzystywane są rezystory. Spełniają one rolę podobną do zaworu zamontowanego w rurze wodociągowej. Gdy go trochę przykręcimy, zmniejszy się przepływ wody. Działanie zaworu możemy porównać do działania rezystora. Im większy rezystor zastosujemy, tym bardziej zmniejszymy przepływ prądu w układzie – tak samo, jak w sytuacji, gdy coraz bardziej  przymykamy zawór.

Jednostką rezystancji jest om, oznaczany grecką literą Ωomega.

Prawo Ohma

Niemiecki fizyk i matematyk Georg Ohm sformułował jedno z najważniejszych praw fizycznych, opisujące zależność pomiędzy napięciem, prądem a rezystancją. Odkrył relacje między tymi wielkościami i zapisał je w postaci wzoru:

gdzie:
I – prąd,
U – napięcie,
R – rezystancja.

Wzór ten został nazwany prawem Ohma. Mówi ono, że prąd przepływający przez obwód jest wprost proporcjonalny do napięcia przyłożonego do obwodu, a odwrotnie proporcjonalny do rezystancji obwodu.

Oznacza to, że jeżeli wzrośnie napięcie w obwodzie, a rezystancja pozostanie taka sama, to wzrośnie również natężenie prądu. Jeżeli z kolei rezystancja wzrośnie, a przyłożone napięcie się nie zmieni, to natężenie prądu się zmniejszy.

Jeśli znamy prąd oraz napięcie, możemy przekształcić przedstawiony wyżej wzór i obliczyć rezystancję:

Znając prąd i rezystancję oraz dokonując kolejnego przekształcenia, jesteśmy w stanie obliczyć napięcie:

Rezystory

Rezystory mają nieskomplikowaną budowę: przypominają walce z dwiema nóżkami. Na korpusie rezystora umieszczane są oznaczenia w postaci kolorowych pasków. Takich pasków może być cztery, pięć lub sześć. Pozwalają one odczytać wartość rezystancji oraz dodatkowe parametry.

Kolejne paski od lewej strony określają:

• pierwszą cyfrę,

• drugą cyfrę,

• opcjonalnie trzecią cyfrę (w przypadku pięcio- oraz sześciopaskowych oznaczeń),

• mnożnik,

• tolerancję,

• współczynnik temperaturowy (w przypadku sześciopaskowych oznaczeń).

R1K2W6GsaexbM

Zdjęcie przedstawia kilka oporników obok siebie. Opornik ma kształt niewielkiego walca i ma dwa wyprowadzenia z górnej i dolnej części wychodzi drut. Na oporniku znajduje się kilka kolorowych pasków. Ich kolory mają znaczenie, określają wartość oporności, tolerancję i współczynnik temperatury.

Załóżmy, że opornik na obudowie ma dwa paski czerwone, jeden brązowy, a następny jest złoty. Odszukajmy kolory pasków w tabeli oraz zapiszmy kolejne wartości.

Wzór, który pozwoli uzyskać wartość rezystancji, ma postać: (pierwsza i druga cyfra) ⋅ mnożnik ± tolerancja. Zatem w przypadku naszego rezystora otrzymujemy:

Szeregowe łączenie rezystorów

Rezystancję w obwodzie możemy zmieniać nie tylko przez zastąpienie jednego rezystora innym, mającym większą lub mniejszą oporność. Rezystory możemy także łączyć szeregowo lub równolegle. Załóżmy, że mamy do dyspozycji tylko rezystory o oporności 100 $\Omega$, a potrzebny jest nam rezystor o oporności 200 $\Omega$. W takiej sytuacji wystarczy, że połączymy dwa rezystory 100 $\Omega$ szeregowo. W ten sposób otrzymamy rezystancję zastępczą obwodu równą 200 $\Omega$.

RHr1wFYNWzmvB

Na rysunku przedstawiono szeregowe rozmieszczenie rezystorów. W jednej linii, w niewielkiej odległości narysowano dwa rezystory w kształcie prostokątów. Są umieszczone jeden obok drugiego. Pierwszy z nich opisano jako R1 z wartością 100 omów, drugi jako R2 z wartością 100 omów.

Oto wzór na obliczenie rezystancji zastępczej dwóch rezystorów połączonych szeregowo:

Równoległe łączenie rezystorów

A co należy zrobić, jeśli potrzebujemy opornika o mniejszej rezystancji niż ta, którą mają posiadane rezystory? Na ratunek przychodzi łączenie równoległe rezystorów.

R1PY1UM8Wj3A2

Na rysunku przedstawiono równoległe rozmieszczenie rezystorów. Narysowano duży prostokąt, tak że lewy i prawy bok są krótsze, a górny i dolny bok są dłuższe. Przy krótszych bokach prostokąta narysowano linie, wyprowadzenia. Na jednym z dłuższych boków umieszczono rezystor R1 z wartością 100 omów. Ma kształt mniejszego prostokąta. Na przeciwnym, dłuższym boku prostokąta zamieszczono rezystor R2 z wartością 100 omów. Ma kształt mniejszego prostokąta.

Aby obliczyć rezystancję zastępczą (całkowitą) dwóch połączonych równolegle rezystorów, korzystamy ze wzoru:

Podstawiając wartości 100 $\Omega$ otrzymamy:

Dzielnik napięcia

Dzielnik napięcia jest układem zbudowanym z dwóch rezystorów połączonych szeregowo. Ma on za zadanie zmniejszyć napięcie wyjściowe, tak, aby było ono bezpieczne dla naszych układów elektronicznych.

RURPSbtOuEibu

Na rysunku przedstawiono układ składający się z dwóch rezystorów połączonych ze sobą szeregowo. Rezystor R1 znajduje się nad rezystorem R2. Pomiędzy połączonymi linią rezystorami R1 a R2, w połowie znajduje się linia, wyprowadzenie w prawo. Przy rezystorze R1 pojawia się napięcie U1 ze strzałką skierowaną w górę. Przy rezystorze R2 pojawia się napięcie U2 ze strzałką skierowaną ku górze. Pomiędzy rezystorami, w kierunku od rezystora R2 do R1 pojawia się napięcie U we ze strzałką skierowaną ku górze. Natomiast między rezystorem R2 a punktem wyprowadzenia w prawo pojawia się napięcie U wy ze strzałką skierowaną ku górze.

Oznaczenia na schemacie:

• UIndeks dolny we_we – napięcie wejściowe,

• UIndeks dolny wy_wy – napięcie wyjściowe,

• RIndeks dolny 1₁ oraz RIndeks dolny 2₂ – rezystory,

• UIndeks dolny 1₁ oraz UIndeks dolny 2₂ – spadki napięcia na rezystorach.

Na schemacie widzimy połączone szeregowo rezystory. Suma spadków napięćspadek napięciaspadków napięć na rezystorach jest równa napięciu wejściowemu (wynika to z tzw. drugiego prawa Kirchhoffa):

natomiast napięcie wyjściowe równe jest spadkowi napięcia na rezystorze RIndeks dolny 2₂:

Korzystając z prawa Ohma:

otrzymujemy:

Również z prawa Ohma wiadomo, że:

Podstawiając w miejsce symbolu prądu (I) wzór do jego obliczenia UIndeks dolny we_we/(RIndeks dolny 1₁+RIndeks dolny 2₂)Indeks dolny ,  Indeks dolny koniec_, otrzymujemy wzory na obliczenie napięcia UIndeks dolny 1  Indeks dolny koniec₁ oraz UIndeks dolny 2₂:

Dla ułatwienia obliczeń przestawmy składniki wyrażenia:

Jak napisaliśmy wcześniej, UIndeks dolny wy_wy = UIndeks dolny 2₂, dzięki czemu otrzymujemy końcowy wzór na obliczenie napięcia wyjściowego:

Bramki logiczne

W technice cyfrowej wszystkie działania wykonywane są za pomocą operacji logicznych. Wykorzystuje się do tego dwa stany: stan wysoki – logiczne „1” (prawda) oraz stan niski – logiczne „0” (fałsz). Stany te nie mają przypisanych konkretnych wartości fizycznych, takich jak choćby poziom napięcia, ale przyjmijmy (dla ułatwienia pracy z platformą Arduino), że stanowi wysokiemu odpowiada napięcie 5 V, a stanowi niskiemu – napięcie 0 V. Elementami wykonującymi działania takie jak suma czy iloczyn są bramki logiczne.

Bramka NOT

Najprostszą bramką logiczną jest bramka NOT, która realizuje operację negacji logicznej. Jej zadaniem jest odwrócenie stanu podanego na wejście; jeżeli podamy na wejście stan wysoki, na wyjściu otrzymamy stan niski. Gdy na wejście podamy stan niski, to na wyjściu otrzymamy stan wysoki.

RirGCHYqYZdNt

Na rysunku przedstawiono symbol bramki NOT. Narysowano linię, która styka się z podstawą trójkąta równoramiennego, leżącego na tej linii. Linia oznaczona została literą A. Dalej za prawym wierzchołkiem trójkąta narysowano niewielką kropkę, z której wyprowadzono poziomą linię. Linia opisana jest jako Wyj.

Bramka AND

Kolejną bramką jest bramka AND, która realizuje operację mnożenia. Na wyjściu otrzymamy stan wysoki tylko wtedy, gdy na wszystkich wejściach podamy stan wysoki.

R1PZZp43BaX2P

Na rysunku przedstawiono symbol bramki AND. Narysowano dwie linie, w równym odstępie. Górną opisano literą A, dolną literą B. Obydwie linie narysowano w poziomie, stykają się z bokiem figury. Figura ma kształt pół owala. Z centralnego punktu prawej krawędzi figury, łuku, wyprowadzono linię w poziomie. Opisana została jako Wyj.

Bramka NAND

Bramka NAND to połączenie bramki NOT z bramką AND. Jeżeli spojrzymy na tabelę prawdy bramki NAND, to zobaczymy odwrotną sytuację niż w przypadku bramki AND. Wynika z tego, że logiczne zero otrzymamy na wyjściu tylko wtedy, gdy na wszystkich wejściach będą podane stany wysokie (logiczne 1).

RV5j7mw1JLdUW

Na rysunku przedstawiono symbol bramki NAND. Narysowano dwie linie, w równym odstępie. Górną opisano literą A, dolną literą B. Obydwie linie narysowano w poziomie, stykają się z bokiem figury. Figura ma kształt pół owala. W centralnym punkcie prawej krawędzi figury, łuku, umieszczono niewielką kropkę. Stąd wyprowadzono linię w poziomie. Opisana została jako Wyj.

Bramka OR

Bramka OR jest bramką realizującą operację sumy logicznej. Oznacza to, że wystarczy podać stan wysoki przynajmniej na jedno wejście, aby na wyjściu uzyskać stan wysoki.

R1R89KVbTn1hb

Na rysunku przedstawiono symbol bramki OR. Narysowano dwie linie, w równym odstępie. Górną opisano literą A, dolną literą B. Obydwie linie narysowano w poziomie, stykają się z bokiem figury. Figura ma kształt rybiego ogona. W centralnym punkcie prawej krawędzi figury wyprowadzono linię w poziomie. Opisana została jako Wyj.

Bramka NOR

Bramka NOR to połączenie bramki NOT z bramką OR. Stany wyjściowe bramki NOR są odwrotnością stanów wyjściowych bramki OR. W przypadku tej bramki na wyjściu otrzymamy stan wysoki tylko wtedy, gdy na wszystkich wejściach podamy stan niski.

RERekUW7UNmZA

Na rysunku przedstawiono symbol bramki NOR. Narysowano dwie linie, w równym odstępie. Górną opisano literą A, dolną literą B. Obydwie linie narysowano w poziomie, stykają się z bokiem figury. Figura ma kształt rybiego ogona. W centralnym punkcie prawej krawędzi figury, umieszczono niewielką kropkę. Stąd wyprowadzono linię w poziomie. Opisana została jako Wyj.

Bramka XOR

Za realizację funkcji różnicy symetrycznej odpowiada bramka XOR. Z jej tablicy prawdy wynika, że stan wysoki na wyjściu pojawia tylko wtedy, gdy na wejścia podamy różne stany logiczne, np: 0 i 1 lub 1 i 0.

R1YTQvDgMfkN8

Na rysunku przedstawiono symbol bramki XOR. Narysowano dwie linie, w równym odstępie. Górną opisano literą A, dolną literą B. Obydwie linie narysowano w poziomie, stykają się z pionową linią, która narysowana została w niewielkiej odległości od boku figury. Figura ma kształt rybiego ogona. W centralnym punkcie prawej krawędzi figury wyprowadzono linię w poziomie. Opisana została jako Wyj.

Bramka XNOR

Bramka XNOR to połączenie bramki XOR z bramką NOT. Realizuje ona funkcję zaprzeczenia różnicy symetrycznej. Z tablicy prawdy odczytujemy, że stan wysoki na wyjściu otrzymamy tylko wtedy, gdy na wejścia podamy takie same stany, czyli np: 0 i 0 oraz 1 i 1.

R182vNl3zs3NS

Na rysunku przedstawiono symbol bramki XNOR. Narysowano dwie linie, w równym odstępie. Górną opisano literą A, dolną literą B. Obydwie linie narysowano w poziomie, stykają się z pionową linią, która narysowana została w niewielkiej odległości od boku figury. Figura ma kształt rybiego ogona. W centralnym punkcie prawej krawędzi figury umieszczono niewielką kropkę. Stąd wyprowadzono linię w poziomie. Opisana została jako Wyj.

Słownik